-
摘要:
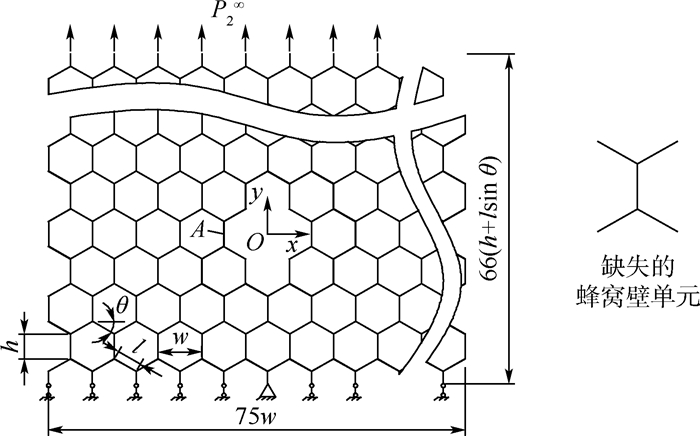
蜂窝或胞壁缺失是蜂窝夹层结构缺陷形式的一种，由于蜂窝（壁）的缺失，导致蜂窝芯子的连续性被破坏，并产生应力集中。本文从蜂窝细观尺度出发，通过数值解析与有限元模拟相结合的方式对缺陷周围胞壁正应力进行分析，首先，通过有限元模拟得到胞壁的拉应力结果，结果表明，应力集中带状区上的胞壁标准化拉应力沿横向符合近似卡方概率密度函数的分布形式；存在一个临界位置使蜂窝壁拉应力分布曲线出现反转。其次，对蜂窝缺陷最大拉应力处的壁内弯矩值与胞壁缺失个数的关系进行了推导。最后，给出了预估弯曲应力的公式，并分析了缺陷形状对预估公式参数的影响。
Abstract:A kind of defect with some of the cell walls missing in a honeycomb structure causes the loss of continuum of the honeycomb, and thus results in the stress concentration around the defect tip. Combined with the finite element and the analytic methods, this paper analyzed the normal stresses distribution on the cell wall at the defect tip in meso-scale. The finite element results of the tensile stress of the cell walls are obtained first. The results shows that the
x -directional stress distribution in the stress concentration strip area fits the probability distribution function of the quasi chi square distribution. There exists a band zone in which the normal stress is much higher than the rest of areas. The distribution of the normal stress of cell walls conform the in the band; there also exists a critical position at which the variation trend of distribution function inverses; secondly, the relation between moments of cell wall and the number of the missing walls is analytically researched. At last. a prediction equation of the bending stress is developed and the influence of defect shape on formula is analyzed.-
Key words:
- honeycomb structure /
- embed structure /
- defect /
- stress concentration /
- finite element method
-
图 2 蜂窝壁单元缺失
σ2, maxP-缺陷蜂窝胞壁拉应力最大值；ycr-临界y值。
Figure 2. Honeycomb with missing cell wall elements
图 3 缺陷蜂窝芯子有限元模型及缺失单元
Figure 3. Finite element model of honeycomb core with defects and corresponding missing element
图 4 应力集中带状区胞壁标准化拉应力分布
Figure 4. Normalized tensile stress distribution of cell walls in stress concentration strip area
图 5 m=3, n=7缺陷附近竖向蜂窝壁内拉应力分布
Figure 5. Tensile stress distribution of y-direction honeycomb walls with defect of m=3, n=7
图 6 m=3, n=3缺陷附近竖向蜂窝壁内拉应力分布
Figure 6. Tensile stress distribution of y-direction honeycomb walls with defect of m=3, n=3
图 7 m=5, n=1缺陷附近竖向蜂窝壁内拉应力分布
Figure 7. Tensile stress distribution of y-directionhoneycomb walls with defect of m=5, n=1
图 8 最大拉应力所在胞壁应力分解
Figure 8. Stress decomposition on cell wall with maximum tensile stress
图 9 最大拉应力处蜂窝壁静力分析
-蜂窝壁A所受y向拉力。
Figure 9. Static analysis of honeycomb walls with maximum tensile stress
表 1 应力集中带状区的胞壁标准化拉应力有限元结果
Table 1. FEM results of normalized tensile stress of cell walls in stress concentration strip area
x/w σ2P/σ2∞ n=4 n=5 n=8 2(2.5) 1.265 7 (1.365 1) 3(3.5) 1.252 9 (1.325 9) 4(4.5) 1.195 1 (1.249 2) 1.628 5 5(5.5) 1.146 7 (1.188 0) 1.528 0 6(6.5) 1.112 3 (1.144 5) 1.403 9 7(7.5) 1.088 3 (1.114 1) 1.308 9 8(8.5) 1.071 5 (1.092 7) 1.241 4 9(9.5) 1.059 4 (1.077 1) 1.193 5 10(10.5) 1.050 5 (1.065 6) 1.158 9 11(11.5) 1.043 9 (1.056 9) 1.133 3 12(12.5) 1.038 9 (1.050 1) 1.114 0 13(13.5) 1.034 9 (1.044 8) 1.099 0 14 1.087 2 15 1.077 8 
下载: 导出CSV
表 2 蜂窝壁横向拉应力值拟合残差
Table 2. Fitting error of x-directional tensile stress of cell walls
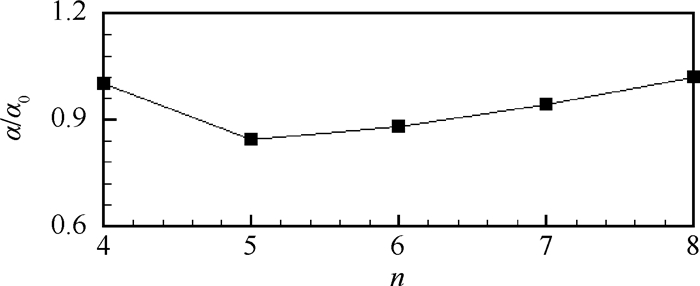
% 公式号 n=4 n=5 n=8 式(3) 0.04 0.07 0.19 式(6) 0.40 0.66 1.80 式(7) 1.98 16.10
下载: 导出CSV
表 3 不同n值时的α/α0
Table 3. Variations of α/α0 with different n
n 4 5 6 7 8 α/α0 1.000 0 0.844 2 0.880 0 0.943 3 1.019 8
下载: 导出CSV
-
[1] GIBSON L J, ASHBY M F.Cellular solids:Structure and properties[M].2nd ed.Cambridge:Cambridge University Press, 1997:98-135. [2] LI Y M, HOANG M P, ABBES F, et al.Analytical homogenization for stretch and bending of honeycomb sandwich plates with skin and height effects[J].Composite Structures, 2015, 120:406-416. doi: 10.1016/j.compstruct.2014.10.028 [3] LIU P, LIU Y, ZHANG X.Internal-structure-model based simulation research of shielding properties of honeycomb sandwich panel subjected to high-velocity impact[J].International Journal of Impact Engineering, 2015, 77:120-133. doi: 10.1016/j.ijimpeng.2014.11.004 [4] COELHO P G, RODRIGUES H C.Hierarchical topology optimization addressing material design constraints and application to sandwich-type structures[J].Structural and Multidisciplinary Optimization, 2015, 52(1):91-104. doi: 10.1007/s00158-014-1220-x [5] LI S Q, LI X, WANG Z H, et al.Finite element analysis of sandwich panels with stepwise graded aluminum honeycomb cores under blast loading[J].Composites Part A:Applied Science and Manufacturing, 2016, 80:1-12. doi: 10.1016/j.compositesa.2015.09.025 [6] BARNETT D M, RAWAL S, RUMMEL K.Multifunctional structures for advanced spacecraft[J].Journal of Spacecraft and Rockets, 2001, 38(2):226-230. doi: 10.2514/2.3674 [7] RAWAL S P, BARNETT D M, MARTIN D E.Thermal management for multifunctional structures[J].IEEE Transactions on Advanced Packaging, 1999, 22(3):379-383. doi: 10.1109/6040.784489 [8] CHEN D H, OZAKI S.Stress concentration due to defects in a honeycomb structure[J].Composite Structures, 2009, 89(1):52-59. doi: 10.1016/j.compstruct.2008.06.010 [9] CHEN T J, HUANG J S.Creep-buckling of hexagonal honeycombs with dual imperfections[J].Composite Structures, 2009, 89(1):143-150. doi: 10.1016/j.compstruct.2008.07.018 [10] CHEN C, LU T J, FLECK N A.Effect of imperfections on the yielding of two-dimensional foams[J].Journal of the Mechanics and Physics of Solid, 1999, 47(11):2235-2272. doi: 10.1016/S0022-5096(99)00030-7 [11] AJDARI A, NAYEB-HASHEMI H, CANAVAN P.Effect of defects on elastic-plastic behavior of cellular materials[J].Materials Science and Engineering:A, 2008, 487(1):558-567. https://www.researchgate.net/publication/223730656_Effect_of_defects_on_elastic-plastic_behavior_of_cellular_materials [12] ZHU K, CUI X D, FANG D N.The reinforcement and defect interaction of two-dimensional lattice materials with imperfections[J].International Journal of Solids and Structures, 2012, 49(13):1908-1917. doi: 10.1016/j.ijsolstr.2012.04.002 [13] CUI X D, ZHANG Y H, ZHAO H.Stress concentration in two dimensional lattices with imperfections[J].Acta Mechanica, 2011, 216(1-4):105-122. doi: 10.1007/s00707-010-0354-1 [14] LI K, GAO X L, SUBHASH G.Effects of cell shape and cell wall thickness variations on the elastic properties of two-dimensional cellular solids[J].International Journal of Solids and Structures, 2005, 42(5):1777-1795. https://www.researchgate.net/publication/223099017_Effects_of_cell_shape_and_cell_wall_thickness_variations_on_the_elastic_properties_of_two-dimensional_cellular_solids [15] WANG A J, MCDOWELL D L.Effects of defects on in-plane properties of periodic metal honeycombs[J].International Journal of Mechanical Sciences, 2003, 45(11):1799-1813. doi: 10.1016/j.ijmecsci.2003.12.007 [16] 宋玉旺, 杨昌昊, 石晓飞, 等.六边形蜂窝夹层板的参数化有限元建模方法[J].计算机辅助设计与图形学学报, 2015, 27(1):175-183. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201501022.htmSONG Y W, YANG C H, SHI X F, et al.Parameterized finite element model of hexagon honeycombs[J].Journal of Computer-Aided Design & Computer Graphics, 2015, 27(1):175-183(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201501022.htm [17] LEYER A.Machine Design[M].London:Blackie & Son, 1974:89-92. -
下载:
点击查看大图
计量
- 文章访问数: 805
- HTML全文浏览量: 107
- PDF下载量: 507
- 被引次数: 0
