-
摘要:
概率假设密度(PHD)滤波算法已被证明是实时多目标跟踪的有效方法,但现有这些基于PHD滤波的方法假设量测噪声协方差先验已知,而实际中量测噪声协方差可能是未知或随着环境改变而变化。针对这一问题,提出了一种适用于非线性量测模型的自适应噪声协方差多目标跟踪算法。该算法以PHD滤波为基础,采用容积卡尔曼(CK)技术近似非线性量测模型,利用逆威沙特(IW)分布描述量测噪声协方差分布,通过变分贝叶斯(VB)近似技术迭代估计量测噪声协方差和多目标状态联合后验密度。仿真结果表明,本文所提算法可有效估计量测噪声协方差,同时实现准确的目标数和目标状态估计。
-
关键词:
- 随机有限集 /
- 多目标跟踪 /
- 未知量测噪声协方差 /
- 变分贝叶斯(VB) /
- 概率假设密度(PHD)滤波
Abstract:Probability hypothesis density (PHD) filter has been demonstrated to be an effective approach for multi-target tracking in real time. However, these methods based on the PHD filter assume that the measurement noise covariance is known as a priori. This is unrealistic for real applications because it may be previously unknown or its value may be time-varying as the environment changes. To solve this problem, an adaptive noise covariance algorithm for multi-target tracking under the nonlinear measurement is proposed. Based on the PHD filter, the proposed algorithm employs the cubature Kalman (CK) technology to approximate the nonlinear model, models the noise covariance distribution as inverse Wishart (IW) distribution, and recursively estimates the joint posterior density of the measurement noise covariance and multi-target states by the variational Bayesian (VB) approach. The simulation results indicate that the proposed algorithm could effectively estimate measurement noise covariance, and achieve the accurate estimation of the target number and corresponding multi-target states.
-
多目标跟踪由于需联合检测和估计时变且未知的目标数和对应目标运动状态,因此一直是目标跟踪领域研究的热点和难点[1-3]。
传统多目标跟踪方法采用数据关联技术,如联合概率数据互联(Joint Probabilistic Data Association,JPDA)[2, 4]、多假设跟踪(Multiple Hypothesis Tracking,MHT)[1, 5]、概率多假设跟踪(Probabilistic MHT,PMHT)[6],但随着目标数或杂波数的增加,其计算量指数增长,严重影响了算法的实时性。
近年来,基于随机有限集(Random Finite Set,RFS)的多目标跟踪方法由于避免了数据关联且提供了一个精确和简洁的公式表示,很快引起广泛关注[3, 7-11]。特别是概率假设密度(Probability Hypothesis Density,PHD)滤波[7-8]、势概率假设密度滤波(Cardinalized PHD Filter,CPHDF)[9-10]和多伯努利滤波(Multi-Bernoulli Filter,MBerF)[3, 11]的发展、实现和应用已经证明了RFS方法的可行性。大部分基于RFS的多目标跟踪方法都是假设量测噪声协方差是先验已知的。然而,在有些应用中,该假设是不成立的,例如对于地面和海面目标的跟踪,量测噪声随着干扰变化,因此量测噪声协方差是未知且时变的。当归一化的量测噪声协方差与真实的噪声过程显著不同时,跟踪方法性能会显著下降。
最近,一些研究者提出了采用变分贝叶斯(Variational Bayesian,VB)方法解决未知量测噪声协方差的问题。文献[12]提出了一种基于VB的自适应噪声协方差PHD滤波。文献[13]提出了一种基于VB的自适应噪声协方差MBerF。文献[14]针对未知噪声协方差下多扩展目标跟踪,给出一种基于VB的MBerF。以上方法采用高斯(Gauss)和逆伽马(Inverse-Gamma,IG)分布来近似联合后验PHD或MBer,但是其仅适用于线性模型的多目标跟踪场景。
针对上述问题,本文提出了一种适用于非线性量测模型的自适应噪声协方差PHD滤波算法,称为自适应容积卡尔曼-VB-PHD (Adaptive Cubature Kalman-VB-PHD,ACK-VB-PHD) 滤波。该算法首先采用CK[15]技术近似非线性量测模型;然后利用逆威沙特(Inverse Wishart,IW)和Gauss乘积混合分布近似量测噪声协方差和多目标状态联合后验分布;最后采用VB近似技术推导滤波迭代。仿真结果表明,本文所提算法对于非线性未知量测噪声协方差场景具有很强的多目标跟踪鲁棒性。本文算法主要通过PHD滤波来实现,可直接推广到CPHDF和MBerF,且可应用于每个目标具有不同量测噪声协方差的非线性场景。
1. 背景理论
1.1 CK滤波
在雷达目标跟踪中,通常采用如下状态方程和量测方程:

(1) 
(2) 式中:F为状态转移矩阵;xk和zk分别为k时刻目标运动状态和量测;ωk和εk分别为过程和量测噪声,其服从零均值协方差分别为Qk和Rk的高斯分布;h(·)为非线性量测函数。因此,雷达目标跟踪是一种非线性滤波问题。
非线性滤波的难点是如何有效计算如下多维积分:

(3) 文献[15]中表明,式(3)的积分可通过采用三阶球面-径向容积准则准确近似,即



相比于扩展卡尔曼和不敏卡尔曼滤波,CK滤波作为一种更有效且适应性更强的非线性滤波得到了广泛应用。
1.2 VB近似
当量测噪声协方差未知且时变时,需要联合估计目标状态和噪声协方差密度。假定目标状态x和噪声协方差R动态模型相互独立,即

(4) 根据贝叶斯滤波准则,其联合后验密度p(xk,Rk|z1:k)计算如下[3]:

(5) 
(6) 由于式(5)的积分很难获得解析计算,研究人员提出了VB近似方法,有效解决了此迭代过程[16]。在该方法中,联合后验密度p(xk,Rk|z1:k)可近似为[17]

(7) 式中:px(xk)和pR(Rk)为未知密度。
真实密度和近似密度的Kullback-Leibler(KL)散度表示为[17]

(8) 为了获得后验密度的最优近似,采用变分计算方法最小化KL散度,可得[17]

(9) 
(10) 当目标状态为Gauss分布,噪声协方差为IW分布,可得[18]

(11) 
(12) 式中:mk和Pk分别为估计状态和协方差;vk和Vk为IW分布参数。
1.3 PHD滤波
假设k时刻有M(k)个目标xk,1,xk,2,…,xk,M(k),每个目标状态取值状态空间χ和N(k)个量测zk,1,zk,2,…,zk,N(k),每个量测取值量测空间


多目标贝叶斯滤波的数学本质是实时迭代传递多目标后验密度,其中多目标状态和多目标量测随机变量采用RFS建模。PHD滤波以一种计算可行的方式近似多目标贝叶斯滤波,通过实时迭代传递后验强度(即多目标后验密度一阶矩)来替代多目标后验密度[3, 7-8]。令Dk|k-1和Dk分别为k时刻的多目标预测和更新强度,则通过PHD滤波迭代实时传递的后验强度可表示为[3, 7]

(13) 
(14) 式中:βk|k-1(x)和γk(x)分别为衍生和新生目标状态预测强度;pS,k(ζ)为存活概率;pD,k(x)为检测概率;κk(·)为服从泊松分布的杂波强度;fk|k-1(·|·)为状态转移密度;gk(·|·)为似然函数。
2. ACK-VB-PHD滤波
假设目标状态x和噪声协方差R相互独立,且目标存活和检测概率不依赖x和R,即pS,k(x,R)=pS,k,pD,k(x,R)=pD,k。转移和量测模型分别为fk|k-1(x|ζ)=N(x;Fζ,Qk)和gk(z|ξ)=N(z;h(ξ),Rk)。在Gauss目标模型假设下,k-1时刻多目标后验强度为Gauss混合形式[8]:

式中:ω为权重系数。同时未知量测噪声协方差条件分布可近似为IW分布,即p(Rk-1|Z1:k-1)=IW(Rk-1;vk-1,Vk-1)。因此,未知量测噪声协方差和状态联合先验强度可近似为

(15) 1) 预测
假设k-1时刻联合后验强度Dk-1|k-1(x,R|Z1:k-1)可被近似为式(15)所示的Gauss与IW乘积的混合形式,则预测联合强度Dk|k-1(x,R)仍然为Gauss与IW乘积的混合形式,且表示为

(16) 式中:

其中:参数ρ满足>0<ρ≤1;矩阵

2) 更新
假设k-1时刻预测联合强度Dk|k-1(x,R)为Gauss与IW乘积的混合形式,即

(17) 且k时刻量测为Zk,则联合后验强度可表示为

(18) 式中:

由于gk(z|x,R)很难获得,因此很难获得强度函数DD,k(x,R|z)的解析计算。利用第 1.2节介绍的VB近似方法,DD,k(x,R|z)可近似表示为

(19) 为了获得强度函数最优近似,采用变分计算方法最小化KL散度:

(20) 可得

(21) 
(22) 最终联合后验强度可近似为

(23) 式(23)中参数通过如下迭代计算获得,由于量测中包含杂波,而杂波会严重影响VB迭代,因此在迭代之时尽可能消除杂波,本文采用距离门方法消除杂波。同时由于量测的非线性,在更新中采用第1.1节介绍的CK技术。具体算法流程如下。
算法 1 ACK-VB-PHD滤波更新

end
end
end
3) 剪枝合并
由于在预测过程中新生目标及衍生目标的加入,以及更新过程中Gauss与IW乘积项的增加,使得最终表示联合后验强度的Gauss与IW乘积项增加。为了减少Gauss与IW乘积项,先删除权重低于门限G的Gauss与IW乘积项,再合并距离在U范围内的Gauss与IW乘积项。
4) 多目标状态提取
类似文献[8]的方法,先估计出目标数,再选取对应数目的权重最大的Gauss与IW乘积项,其Gauss分量的均值作为对应目标状态。
3. 仿真分析
3.1 仿真场景设置
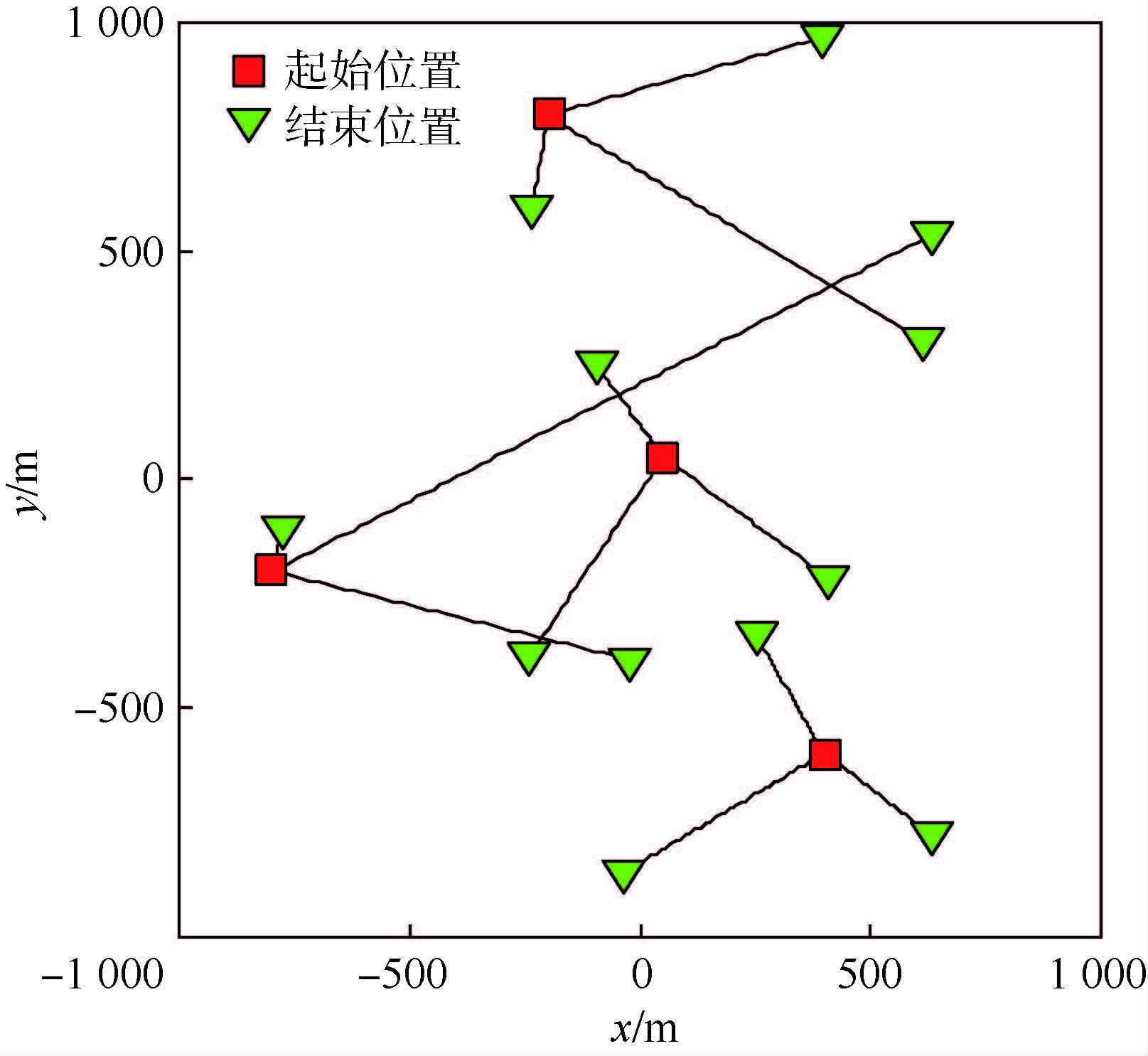
采用一个二维未知且时变多目标场景来验证本文算法。仿真中共有12个目标作匀速运动,如图 1所示。
目标的运动和量测方程如式(1)和式(2)所示,其中




(24) 式中:

退化因子ρ=0.95,距离门Tg=20 m,Gauss与IW乘积项剪枝门限为G=10-5,合并距离门限为U=4 m。杂波在观测区域[0,2π] rad×[0,2 000] m服从泊松分布,强度为λc=4.0×10-3(rad·m)-1(即每帧中平均50个杂波)。
3.2 仿真结果
3.2.1 固定量测噪声协方差
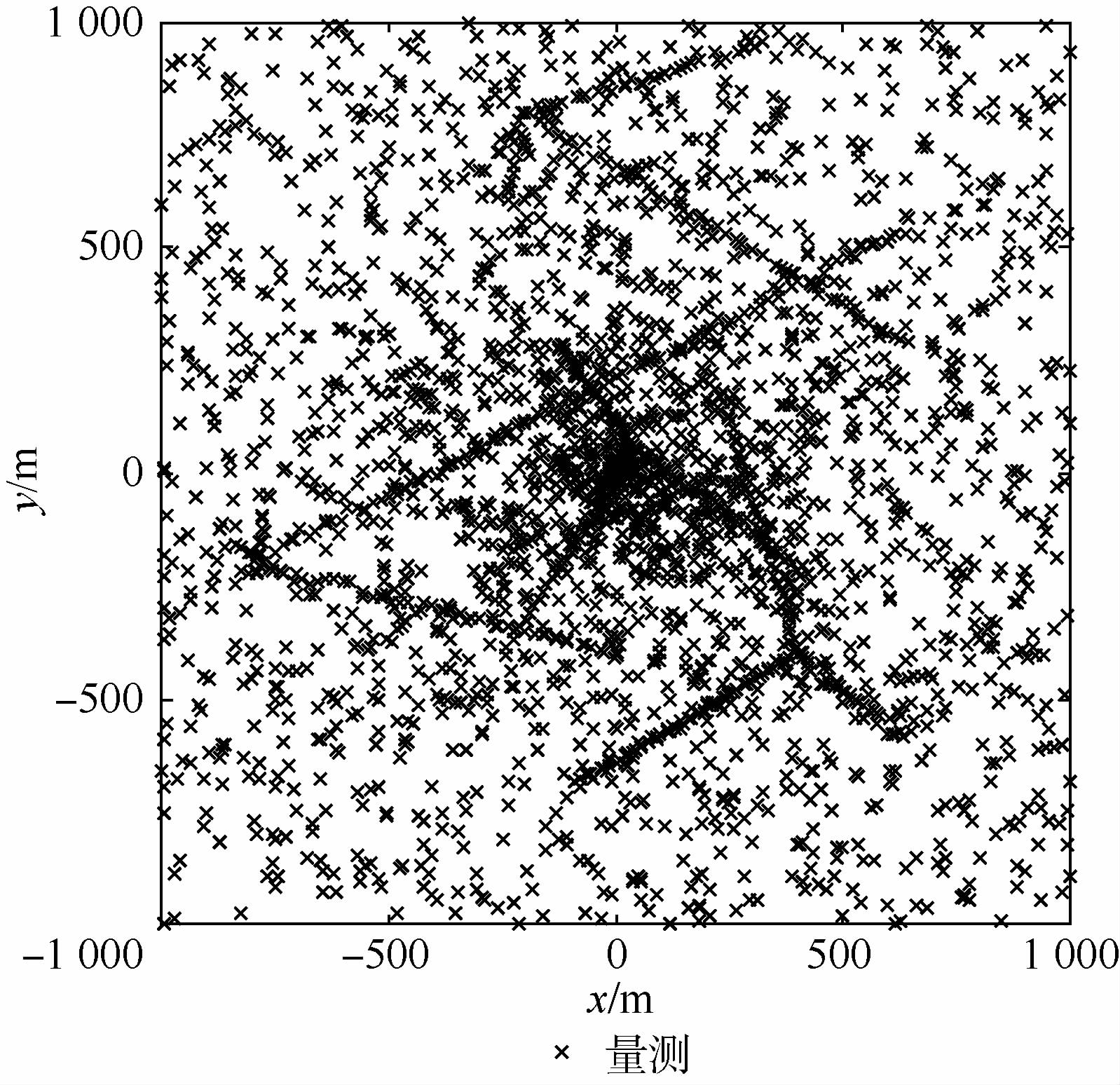
本节采用固定量测噪声协方差的多目标场景来验证本文算法。真实量测噪声εk服从εk~N(·;0,Rk),且Rk=diag([σr2,σθ2]T),σθ=0.2π/180 rad,σr=3 m,其他参数与第3.1节的设置相同。图 2给出了包含杂波的量测。图 3给出了未知量测噪声协方差条件下,ACK-VB-PHD滤波算法单次仿真结果。可以看出,本文所提算法可在未知量测噪声协方差下正确跟踪单独目标运动和不同目标的新生和消失。
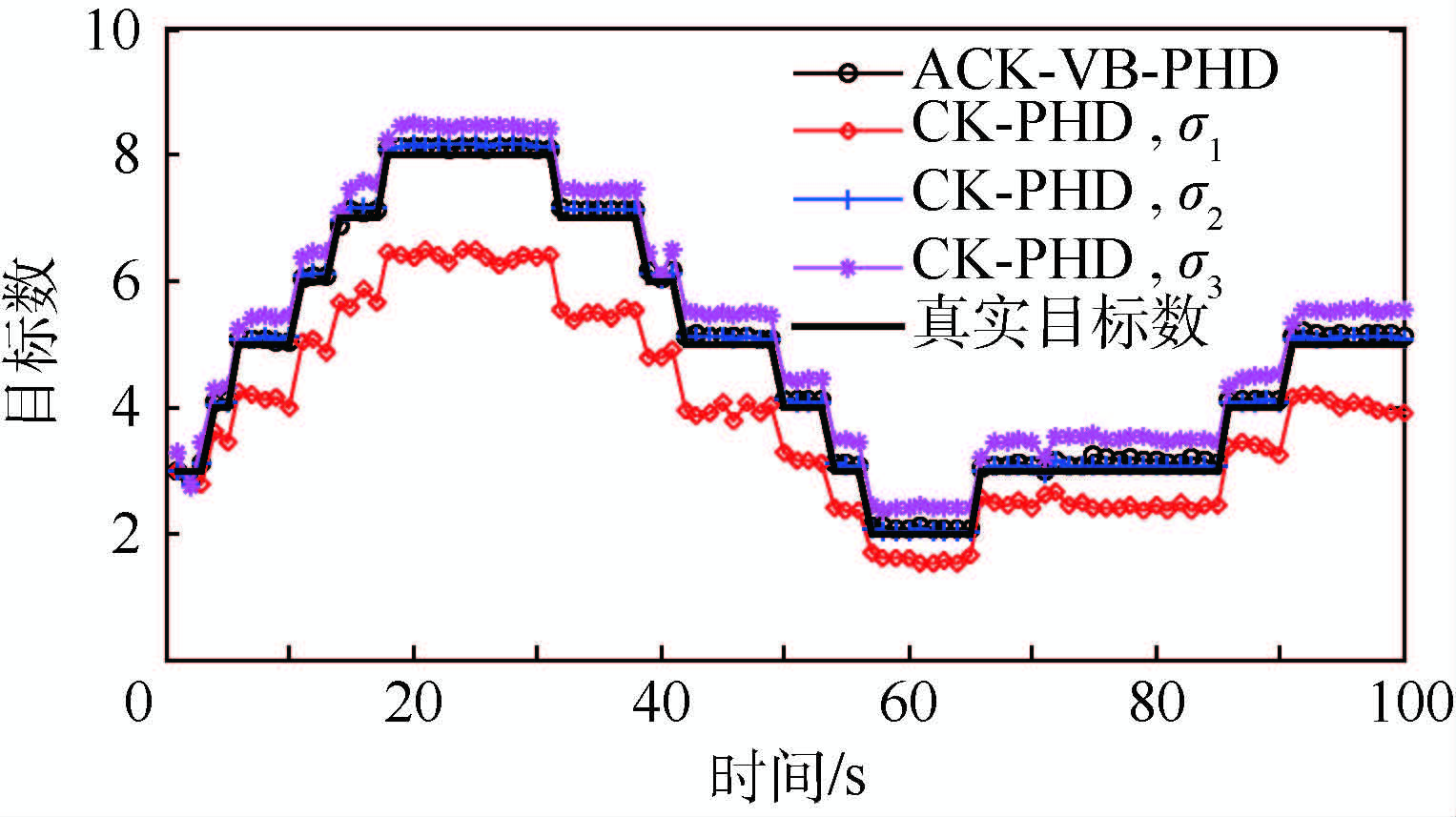
为了进一步验证本文算法的有效性,将其与3种不同量测噪声协方差CK-PHD滤波算法进行比较。分别假设σ1,θ=0.1π/180 rad,σ1,r=1 m; σ2,θ=0.2π/180 rad,σ2,r=3 m;σ3,θ=π/180 rad,σ3,r=10 m。图 4给出了2种算法100次蒙特卡罗仿真实验的目标数估计均值随时间变化曲线。可以看出,ACK-VB-PHD滤波算法可准确估计目标数,与假设 σ2,θ=0.2π/180 rad,σ2,r=3 m的CK-PHD滤波算法性能接近。假设σ3,θ=π/180 rad,σ3,r=10 m的CK-PHD滤波算法估计目标数偏高,而假设σ1,θ=0.1π/180 rad,σ1,r=1 m的CK-PHD滤波算法估计目标数严重偏低。这主要是由于当量测噪声协方差大时,杂波权重增大,目标数为所有权重的和,因此目标数估计偏高;同理当量测噪声协方差小时,真实目标权重变小,杂波强度影响显著目标数估计偏低。
图 5给出了100次蒙特卡罗仿真实验2种算法平均最优子模式分配(Optimal Subpattern Assignment,OSPA)距离[19]随时间变化曲线。可以发现,ACK-VB-PHD滤波算法的OSPA距离接近于假设σ2,θ=0.2π/180 rad,σ2,r=3 m的CK-PHD滤波算法的OSPA距离,且假设σ1,θ=0.1π/180 rad,σ1,r=1 m的CK-PHD滤波算法OSPA距离最差,假设σ3,θ=π/180 rad,σ3,r=10 m的CK-PHD滤波算法OSPA距离次之。这主要是由于ACK-VB-PHD滤波算法可准确估计目标数和跟踪目标,而协方差假设偏大或偏小的CK-PHD滤波算法估计目标数都存在偏差(见图 4),无法准确跟踪目标。
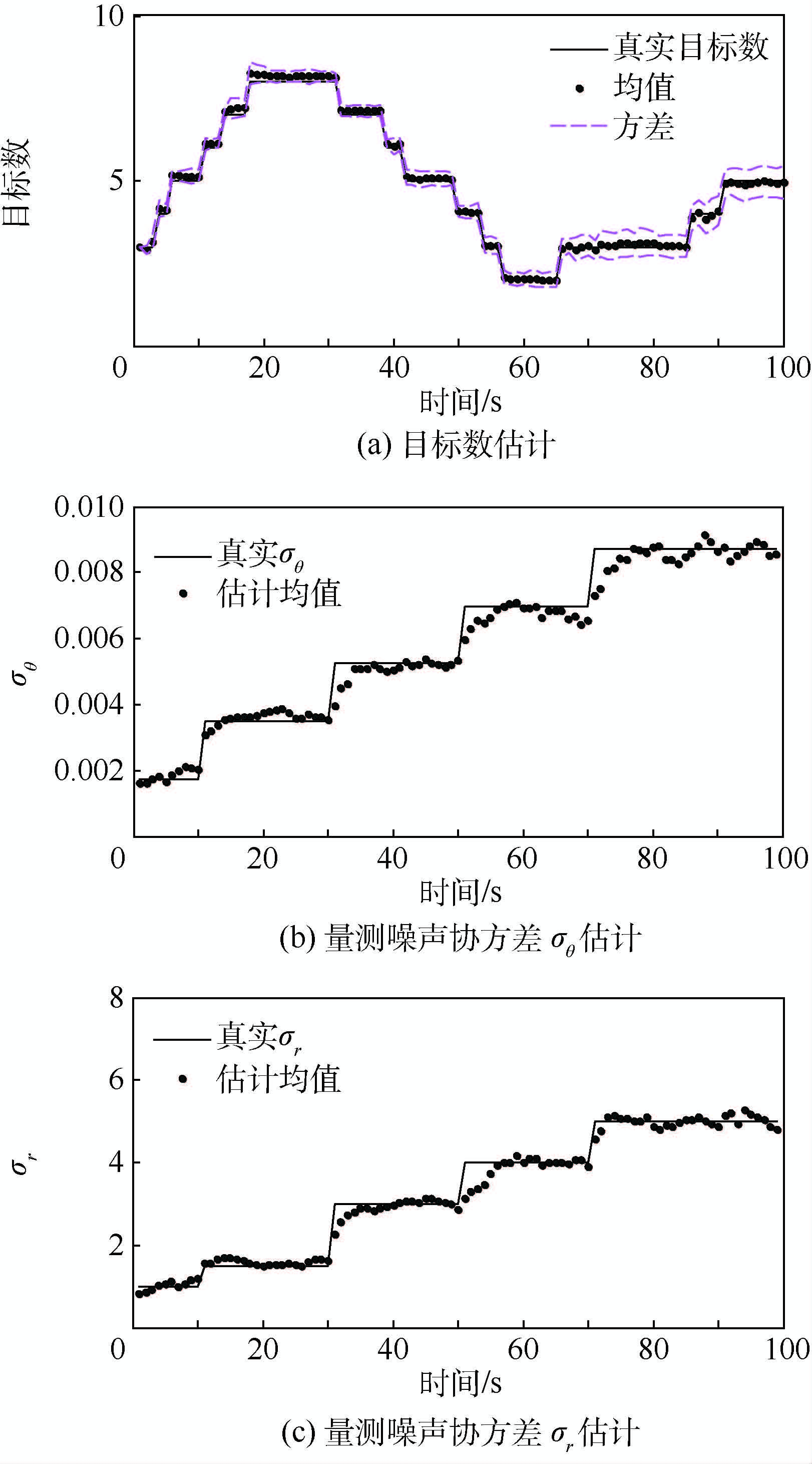
3.2.2 时变量测噪声协方差
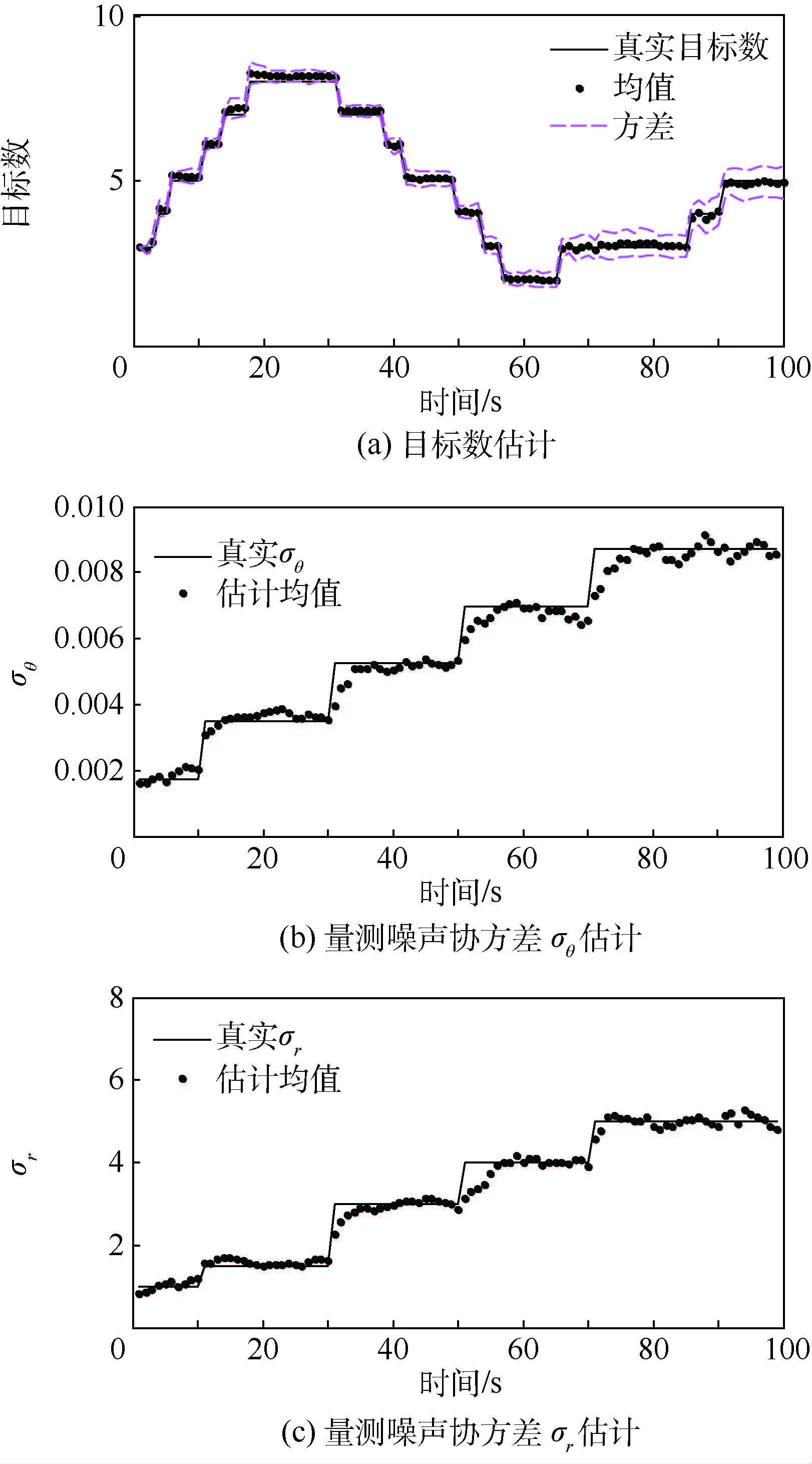
为进一步验证本文算法的鲁棒适应性能,考虑时变量测噪声协方差的多目标运动场景。图 6给出了目标数和量测噪声协方差估计的100次蒙特卡罗结果。可以看出,ACK-VB-PHD滤波算法不仅可准确估计目标数,而且可准确估计时变量测噪声协方差。但是目标数估计方差不断变大主要是由于量测噪声协方差不断增大,量测偏差增大,导致滤波性能下降。
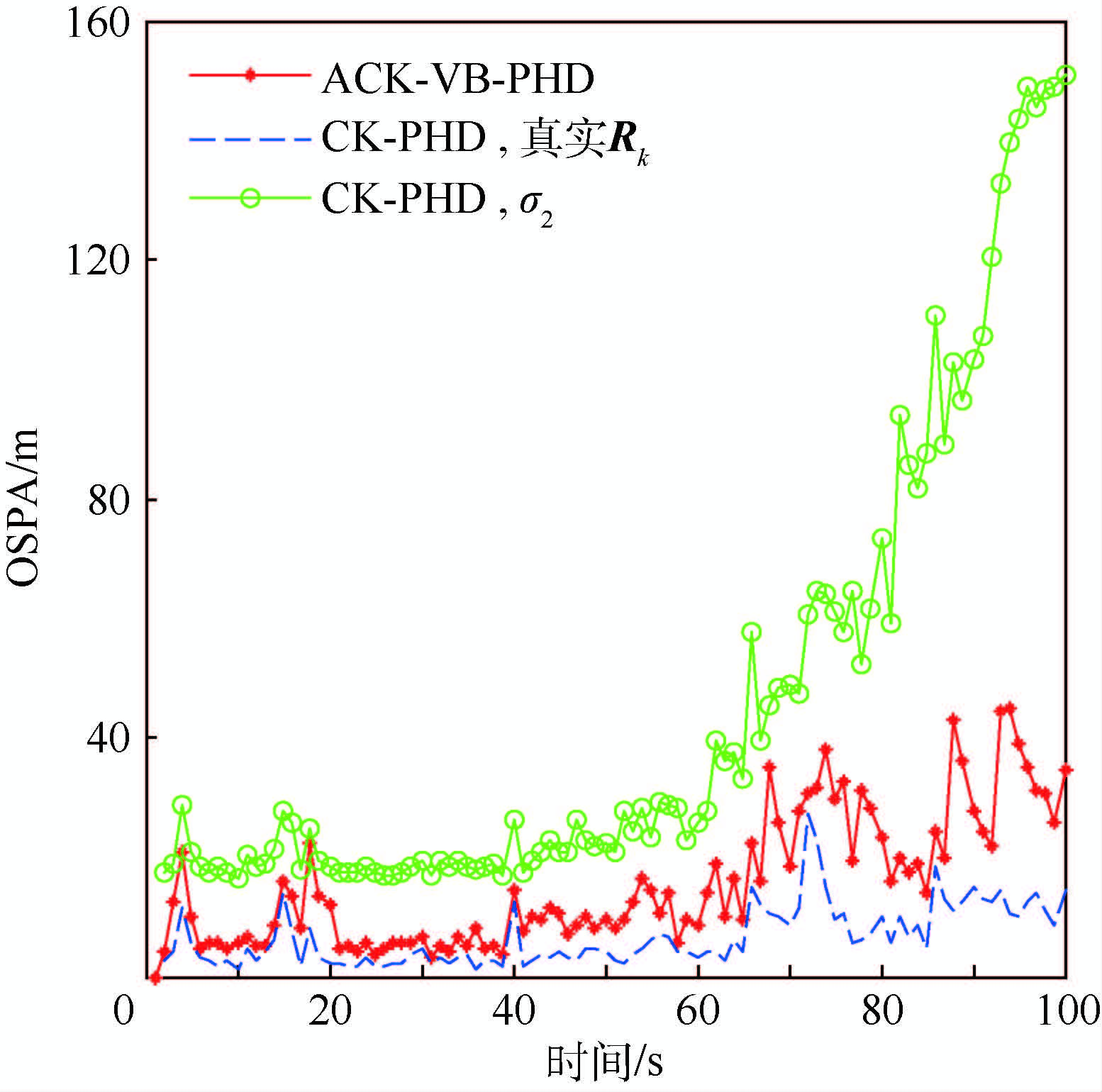
图 7给出了先验已知量测噪声协方差CK-PHD滤波算法、固定量测噪声协方差σ2,θ=0.2π/180 rad,σ2,r=3 m的CK-PHD滤波算法和ACK-VB-PHD滤波算法在时变量测噪声协方差下的100次蒙特卡罗平均OSPA距离。可以看出,ACK-VB-PHD滤波算法的OSPA距离接近于已知量测噪声协方差CK-PHD滤波算法的OSPA距离,但是随着量测噪声协方差不断增大,两者之间差距变大,这主要是由于图 6(a)所示的目标数估计方差增大。但是固定量测噪声协方差CK-PHD滤波算法,其OSPA距离大于另外2种算法,随着量测噪声方差增大,其OSPA距离也在不断增大,这主要由于对于后半部分仿真,假设协方差偏小,导致目标数严重偏低。
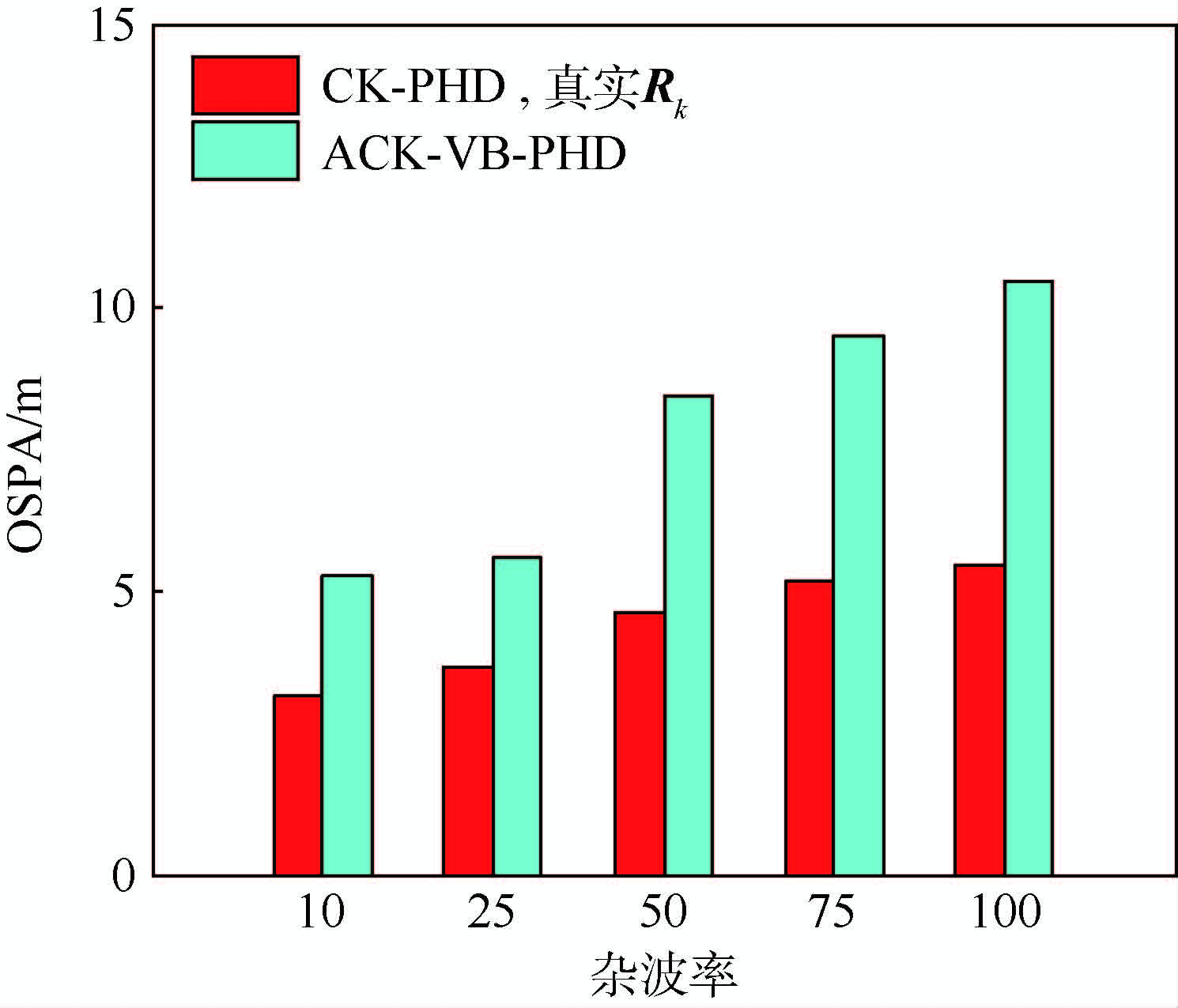
3.2.3 不同杂波率
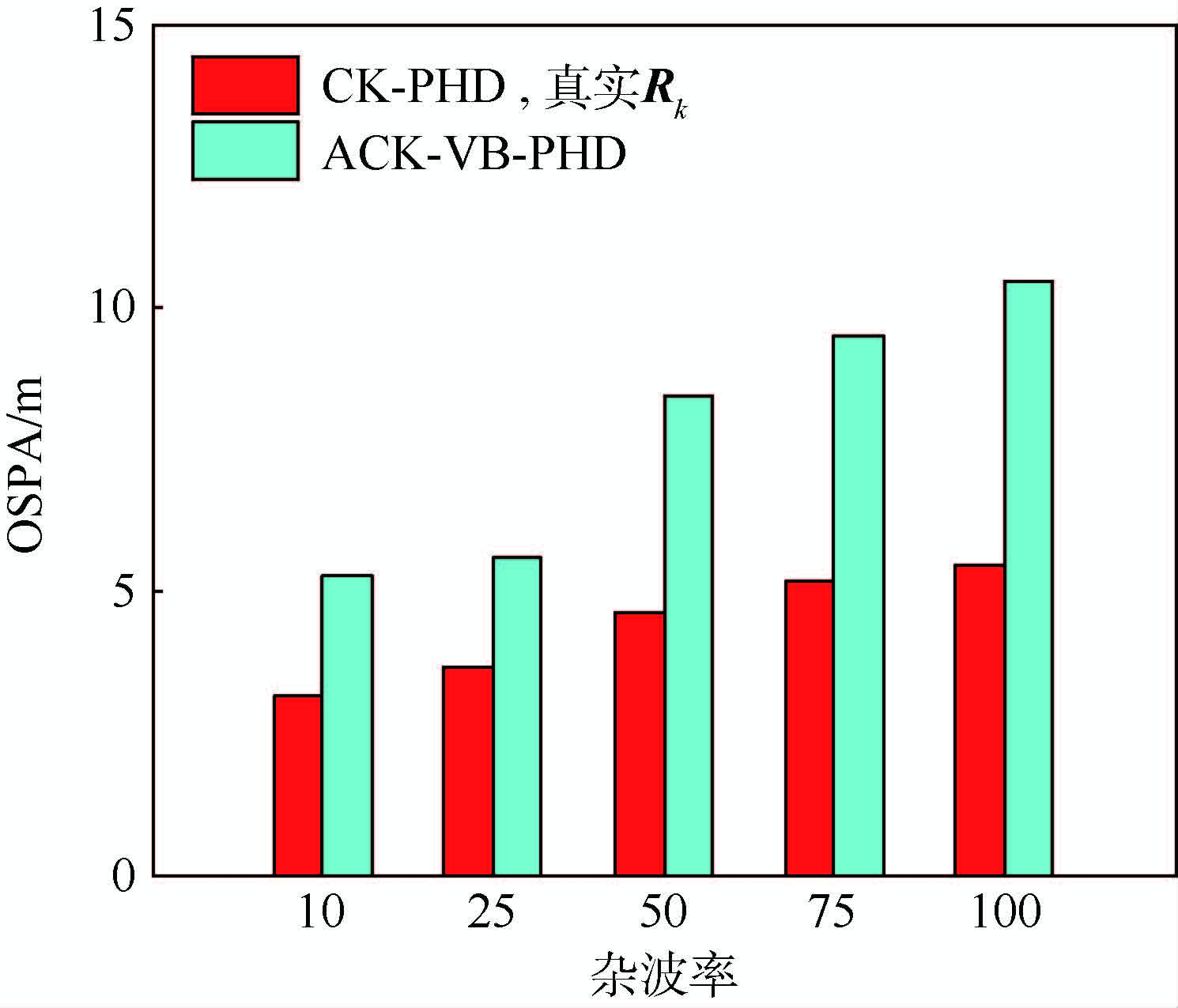
本节讨论杂波率对于滤波性能的影响。图 8给出了固定量测噪声协方差σθ=0.2π/180 rad,σr=3 m,不同杂波率下,先验已知量测噪声协方差CK-PHD滤波和ACK-VB-PHD滤波算法100次蒙特卡罗实验平均OSPA距离。
从图 8中可以看出,随着杂波率提高,2种算法OSPA距离都增大,表明滤波性能都降低,同时两者差距变大。这主要是由于杂波率提高,杂波个数增多,目标数估计误差增大,滤波性能降低,同时杂波影响量测噪声协方差估计准确性。
4. 结 论
本文在PHD滤波算法的基础上,结合CK和VB近似技术,提出了一种非线性量测下未知量测噪声协方差的多目标跟踪算法。仿真结果表明:
1) 本文所提算法可实现对未知量测噪声协方差场景的多目标运动准确跟踪,其目标数估计均值接近于真实目标数;平均OSPA距离为8.5,略高于已知量测噪声协方差的CK-PHD滤波算法。
2) 本文所提算法可实现对于未知且时变量测噪声协方差下的多目标运动准确跟踪和量测噪声协方差准确估计;同时随着量测噪声协方差增大,其目标数估计标准差增大,OSPA距离也相应增大。
3) 本文所提算法随着杂波率增大,滤波性能降低,在杂波率为10时,OSPA距离为5.2,在杂波率为100时,OSPA距离为10.4,性能下降2倍。
本文所提算法采用CK非线性处理,下一步研究非线性模型下性能更优的序贯蒙特卡罗方法对未知量测噪声协方差多目标跟踪。
-
-
[1] BLACKMAN S S.Multiple-target tracking with radar applications[M].Dedham:Artech House,1986:19-44. [2] BAR-SHALOM Y,LI X R,KIRUBARAJAN T.Estimation with applications to tracking and navigation[M].New York:Wiley,2001:21-488. [3] MAHLER R.Statistical multisource-multitarget information fusion[M].Norwood:Artech House,2007:565-682. [4] FORTMANN T E,BAR-SHALOM Y,SCHEFFE M.Sonar tracking of multiple targets using joint probabilistic data ssociation[J].IEEE Journal of Oceanic Engineering,1983,8(3):173-184. doi: 10.1109/JOE.1983.1145560 [5] BLACKMAN S S.Multiple hypothesis tracking for multiple target tracking[J].IEEE Aerospace and Electronic Systems Magazine,2004,19(1):5-18. doi: 10.1109/MAES.2004.1263228 [6] STREIT R L,LUGINBUHL T E.A probabilistic multi-hypothesis tracking algorithm without enumeration and pruning[C]//Proceedings of the 6th Joint Service Data Fusion Symposium.Piscataway,NJ:IEEE Press,1993:1015-1024. [7] MAHLER R.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152-1178. doi: 10.1109/TAES.2003.1261119 [8] VO B N,MA W.The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2006,54(11):4091-4104. doi: 10.1109/TSP.2006.881190 [9] MAHLER R.PHD filters of higher order in target number[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(4):1523-1543. doi: 10.1109/TAES.2007.4441756 [10] VO B T,VO B N,CANTONI A.Analytic implementations of the cardinalized probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2007,55(7):3553-3567. doi: 10.1109/TSP.2007.894241 [11] VO B T,VO B N,CANTONI A.The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J].IEEE Transactions on Signal Processing,2009,57(2):409-423. doi: 10.1109/TSP.2008.2007924 [12] WU X H,HUANG G M,GAO J.Adaptive noise variance identification for probability hypothesis density-based multi-target filter by variational Bayesian approximations[J].IET Radar,Sonar & Navigation,2013,7(8):895-903. [13] YANG J L,GE H W.An improved multi-target tracking algorithm based on CBMeMBer filter and variational Bayesian approximation[J].Signal Processing,2013,93(9):2510-2515. doi: 10.1016/j.sigpro.2013.03.027 [14] LI C Y,WANG R,JI H B.Multiple extended-target tracking based on variational Bayesian cardinality-balanced multi-target multi-Bernoulli[J].Control Theory & Applications,2015,32(2):187-195(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201502007.htm李翠芸,王荣,姬红兵.基于变分贝叶斯势均衡多目标多伯努利滤波的多扩展目标跟踪算法[J].控制理论与应用,2015,32(2):187-195. http://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201502007.htm [15] ARASARATNAM I,HAYKIN S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269. doi: 10.1109/TAC.2009.2019800 [16] SMIDL V,QUINN A.The variational Bayes method in signal processing[M].New York:Springer,2006:15-43. [17] SARKKA S,NUMMENMAA A.Recursive noise adaptive Kalman filtering by variational Bayesian approximations[J].IEEE Transactions on Automatic Control,2009,54(3):596-600. doi: 10.1109/TAC.2008.2008348 [18] SARKKA S,HARTIKAINEN J.Nonlinear noise adaptive Kalman filtering via variational Bayes[C]//IEEE International Workshop on Machine Learning for Signal Processing.Piscataway,NJ:IEEE Press,2013:1-6. [19] SCHUHMACHER D,VO B T,VO B N.A consistent metric for performance evaluation of multi-object filters[J].IEEE Transactions on Signal Processing,2008,56(8):3447-3457. doi: 10.1109/TSP.2008.920469 期刊类型引用(1)
1. 李浩宇,索继东. 未知量测噪声分布下的多扩展目标CBMeMBer滤波算法. 现代电子技术. 2022(19): 66-70 .  百度学术
百度学术其他类型引用(2)
-








 下载:
下载:







 下载:
下载:


 百度学术
百度学术