反作用轮是进行卫星姿态控制的主要部件，卫星通过调节反作用轮转速，使反作用轮角动量与卫星角动量进行交换达到卫星姿态转角控制的作用^[1]。在对于卫星地面验证具有重要意义的半物理仿真试验中，应用力矩测量系统将反作用轮实时输出力矩值引入控制闭环是一种反作用轮参与闭环仿真的新方法，它相比于传统的反作用轮闭环方法(只将反作用轮利用遥测采集转速引入仿真闭环的“转速闭环”方法以及只将卫星动力学模型闭环而使反作用轮只接收遥测指令的“模型闭环反作用轮开环”方法)具有更好的实时性，与真实系统一致性等优点。

但将反作用轮实时力矩引入闭环的过程中，存在外力矩引入卫星动力学模型。因而，模型需利用调节反作用轮转速变化抵消外力矩干扰，而这将极大地影响反作用轮的正常使用及试验的准确运行。特别是在半物理仿真试验进入长时间卫星对地稳定环节，在试验过程中，由于外力矩的引入，为了保持卫星姿态稳定，迫使反作用轮转速以一定加速度加速以抵消外力矩干扰，致使转速沿着某一方向上升，直至超出转速阈值。该现象影响了半物理闭环仿真的有效性，并且极易对反作用轮造成损害。因此，为了保证这一更好的反作用轮闭环仿真方法引入，外力矩误差需要有效补偿。目前，工程中多采用初始人为补偿方法，即观测一段时间系统输出，手动输入补偿值对力矩测量系统输出进行校准，进而消除仿真试验中外力矩干扰。但人为校准存在诸多问题，首先，校准必会受人为因素等误差干扰；再者，由于在仿真试验中，反作用轮起旋后，反作用轮持续作用，无法人为估计补偿量，因此，人为校准只能在初始时刻补偿。最后，初始上电时，力矩测量系统误差跳变较大，致使人为对初始误差的补偿很可能造成更大的输出偏差。

小波滤波方法具有广泛的函数适应性及最优的自适应降噪能力^[2-3]。其优势在于在信号的短时高频部分，短支撑的小波函数起较大作用；而在长时低频部分，长支撑的小波起较大作用^[4]。因此，小波在工程中得到了广泛的应用，不仅在惯性导航器件的漂移校准中大量使用^[5-7]，同时在噪声复杂难以辨识的其他工程领域中应用也极为方便^[8-10]。

在本文中，首先，经对卫星模型外力矩引入数据及力矩测量系统输出误差数据分析后，确定力矩测量系统为仿真闭环试验外力矩干扰源。而后，根据力矩系统输出误差特性，基于小波阈值滤波原理，分别讨论了初始时刻及仿真过程中系统输出误差的补偿方法。提出了采用实时小波滤波法对系统初始输出误差进行补偿；基于反演法原理采用基于小波去噪后的均值滤波算法对仿真过程中误差进行补偿。最后，将2种方法结合应用于仿真试验中，使力矩测量系统得以有效校准，并保证了反作用轮实时力矩的准确引入，使闭环仿真试验可以长时间准确平稳地运行。

1.   外力矩干扰来源及特性分析

1.1   卫星动力学模型外力矩计算

首先，根据姿态动力学方程式(1)，得到外力矩引入与角动量关系。

式中：H为卫星角动量；M为卫星外力矩；${\bar{\omega }}$为式(2)所示的斜对称矩阵：

式中：ω_x、ω_y、ω_z分别为卫星轨道相对于惯性系的转动角速度。

将式(1)分别沿卫星本体系下x、y、z三轴展开，得到

其中：三轴角动量可由式(4)求出：

式中：J_sat和J_w分别为卫星反作用轮转动惯量矩阵；ω_sat和ω_w为卫星反作用轮角速度。

因此，通过采集多组半物理仿真试验卫星角速度、反作用轮转速及获取卫星及反作用轮转动惯量矩阵，并通过计算卫星三轴角动量实时差分求得角动量导数值，即可求出各组试验的外力矩值。

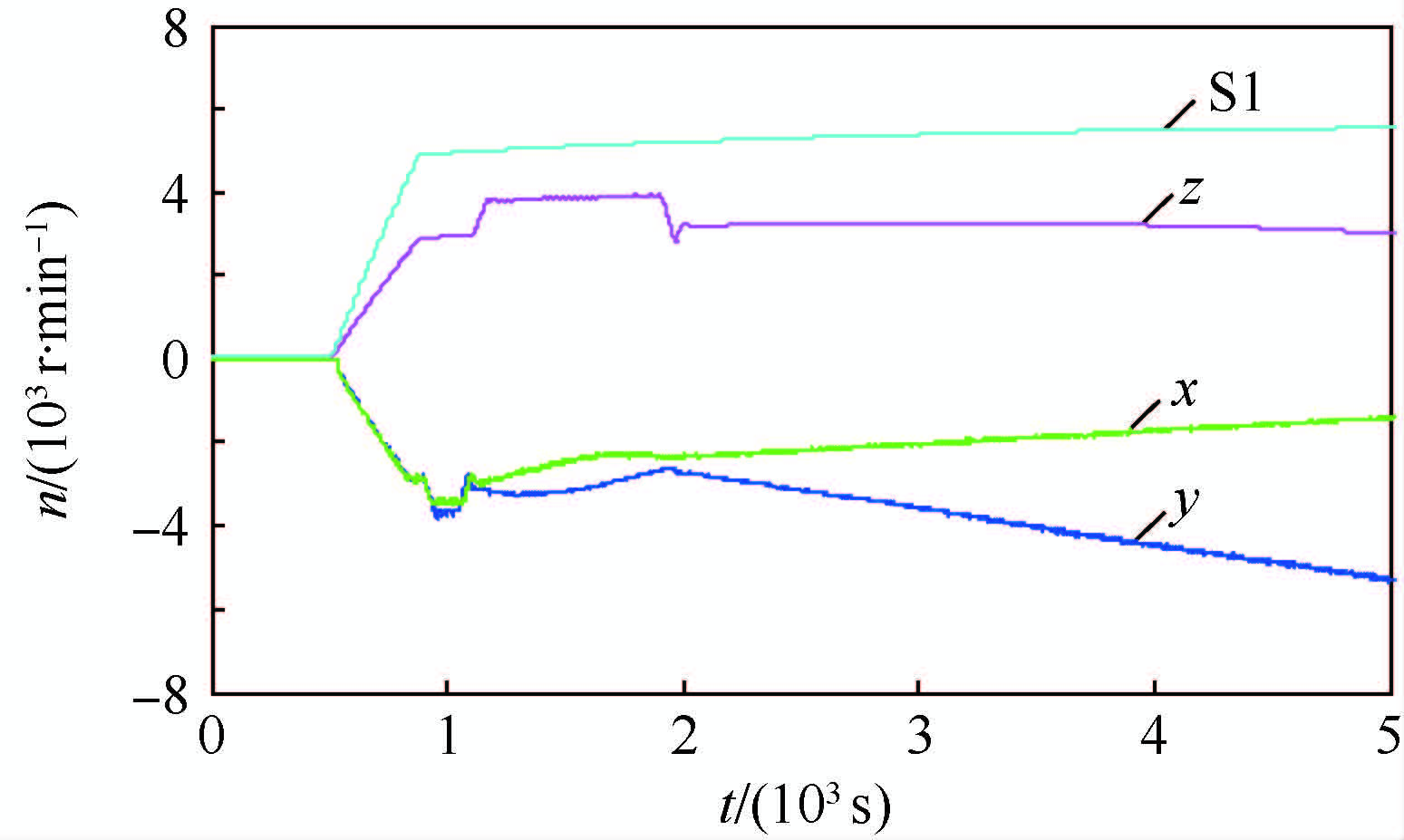
需要指出，试验所使用的卫星动力学模型中反作用轮为三正装、一斜装的结构，但由于条件有限，所进行的试验中x、y轴方向的反作用轮为实物，而z轴方向与斜装方向S1的反作用轮则由数学模型代替，因此，本文主要对仿真过程中x、y轴外力矩引入值与反作用轮转速变化进行讨论。

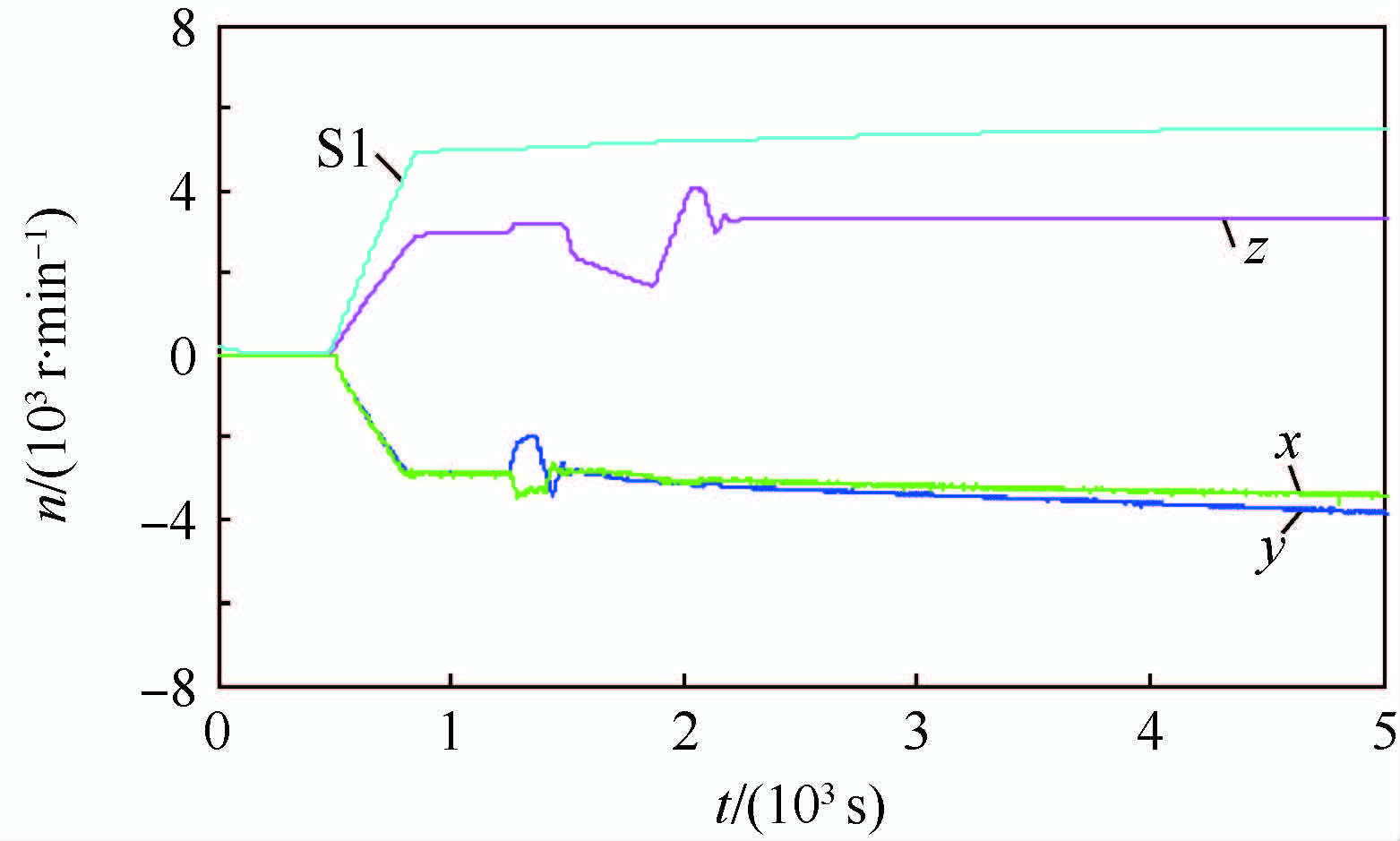
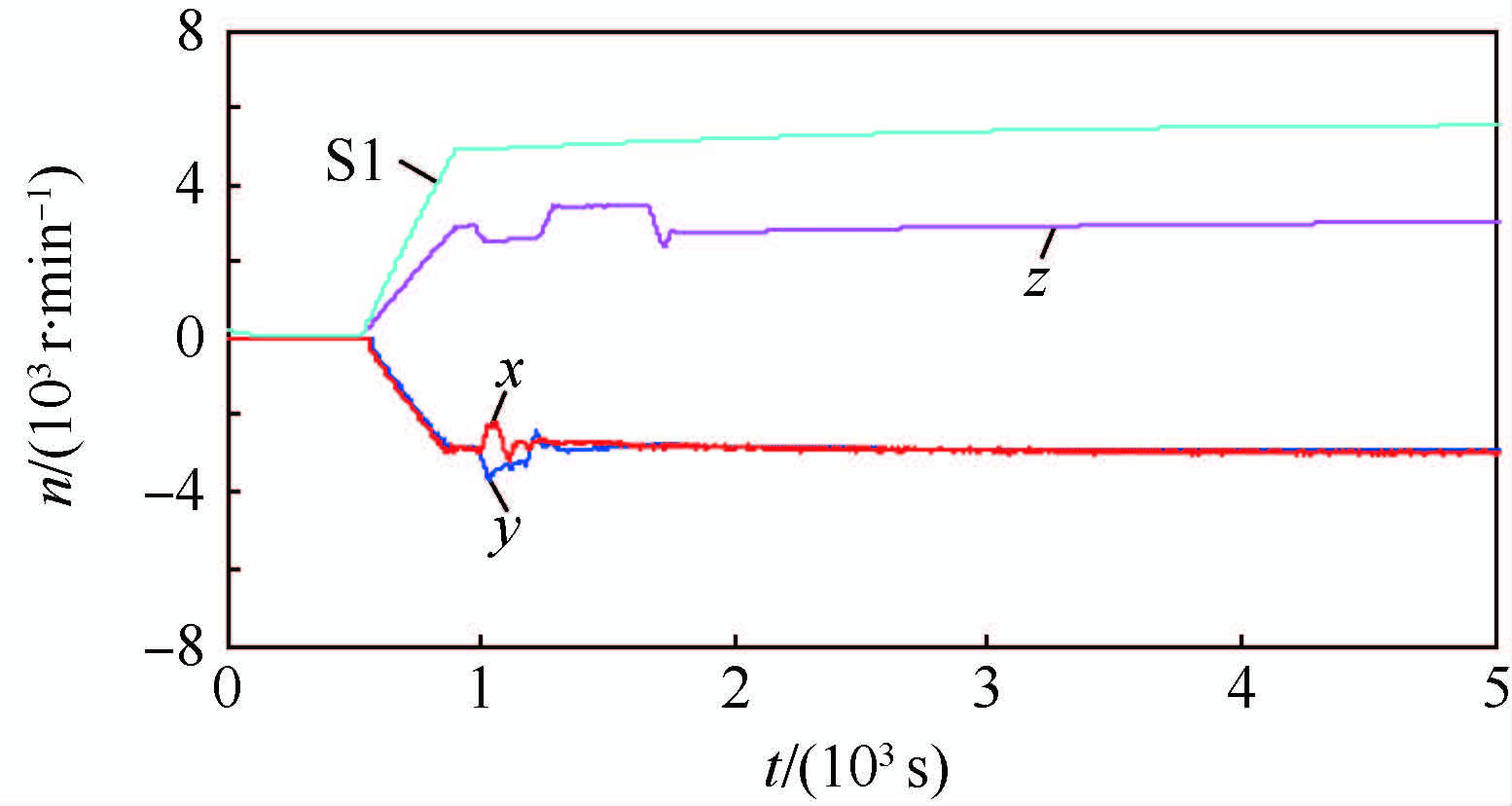
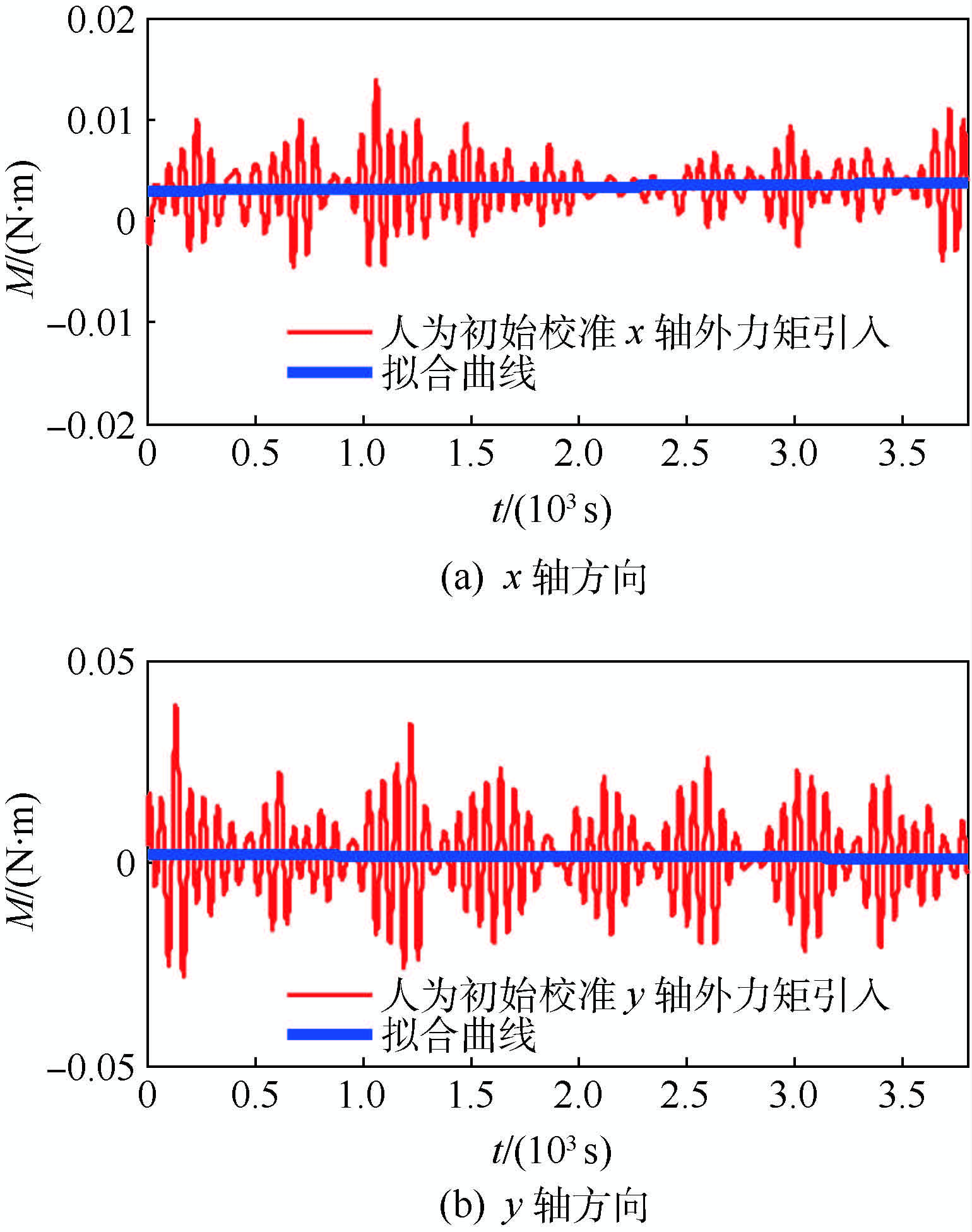
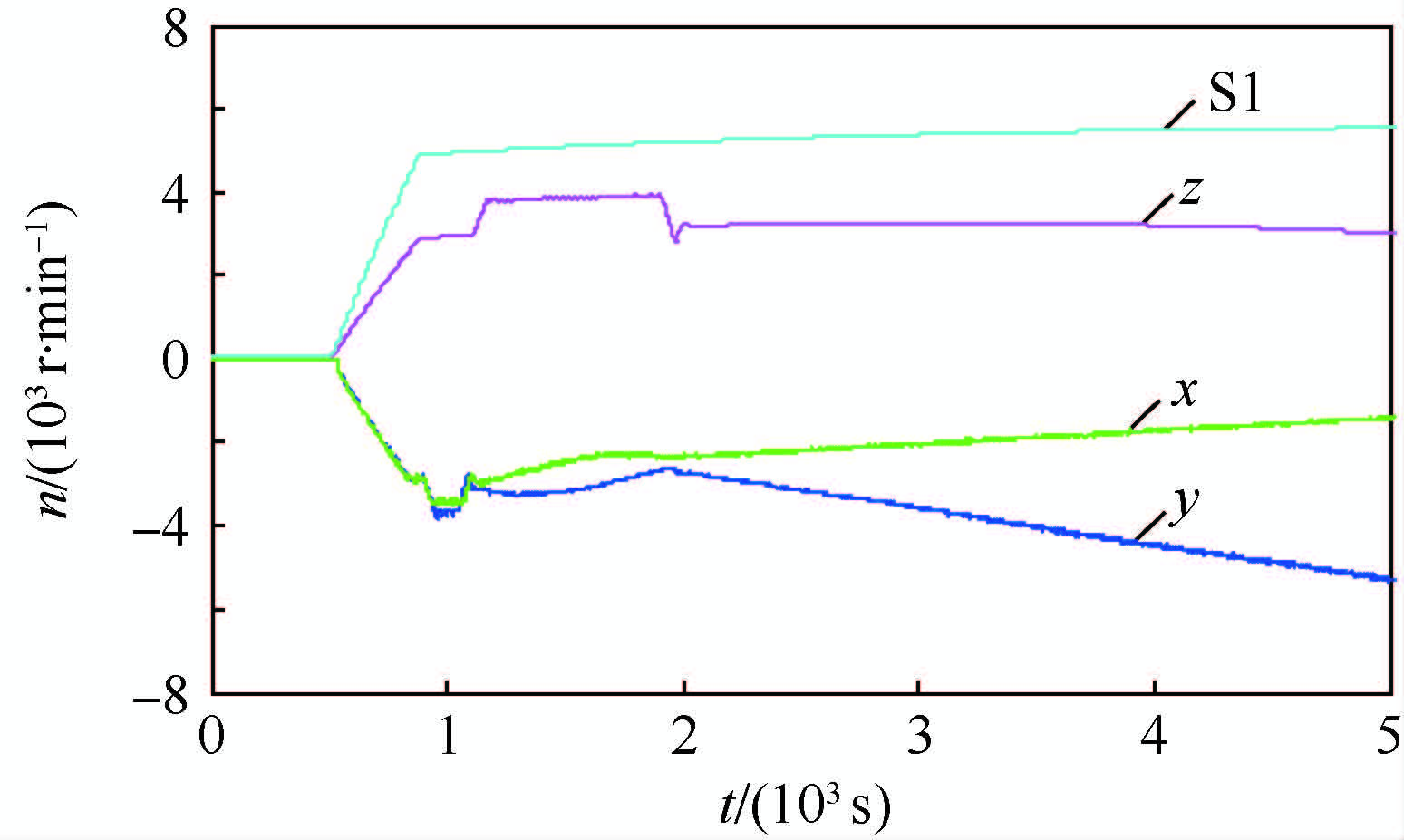
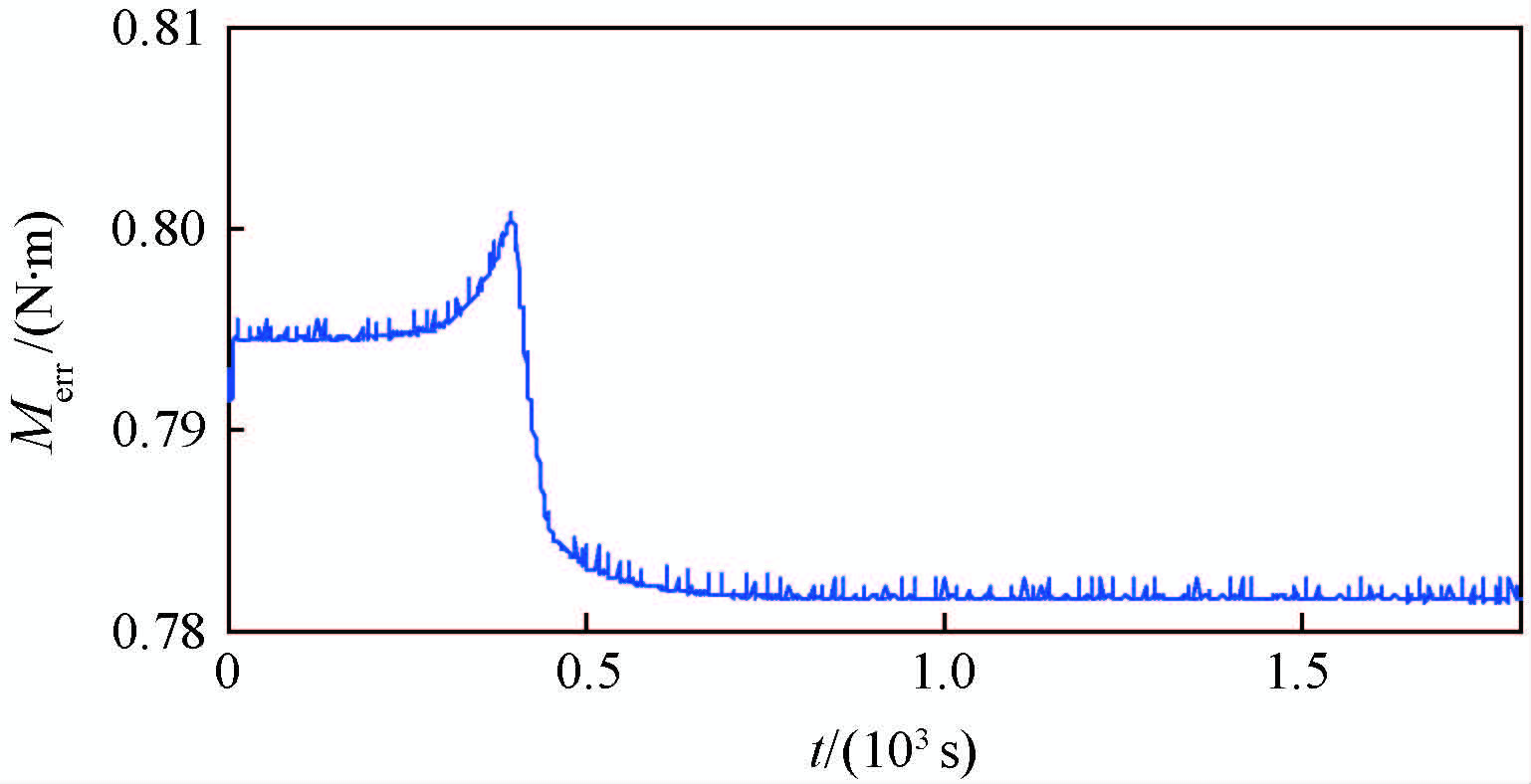
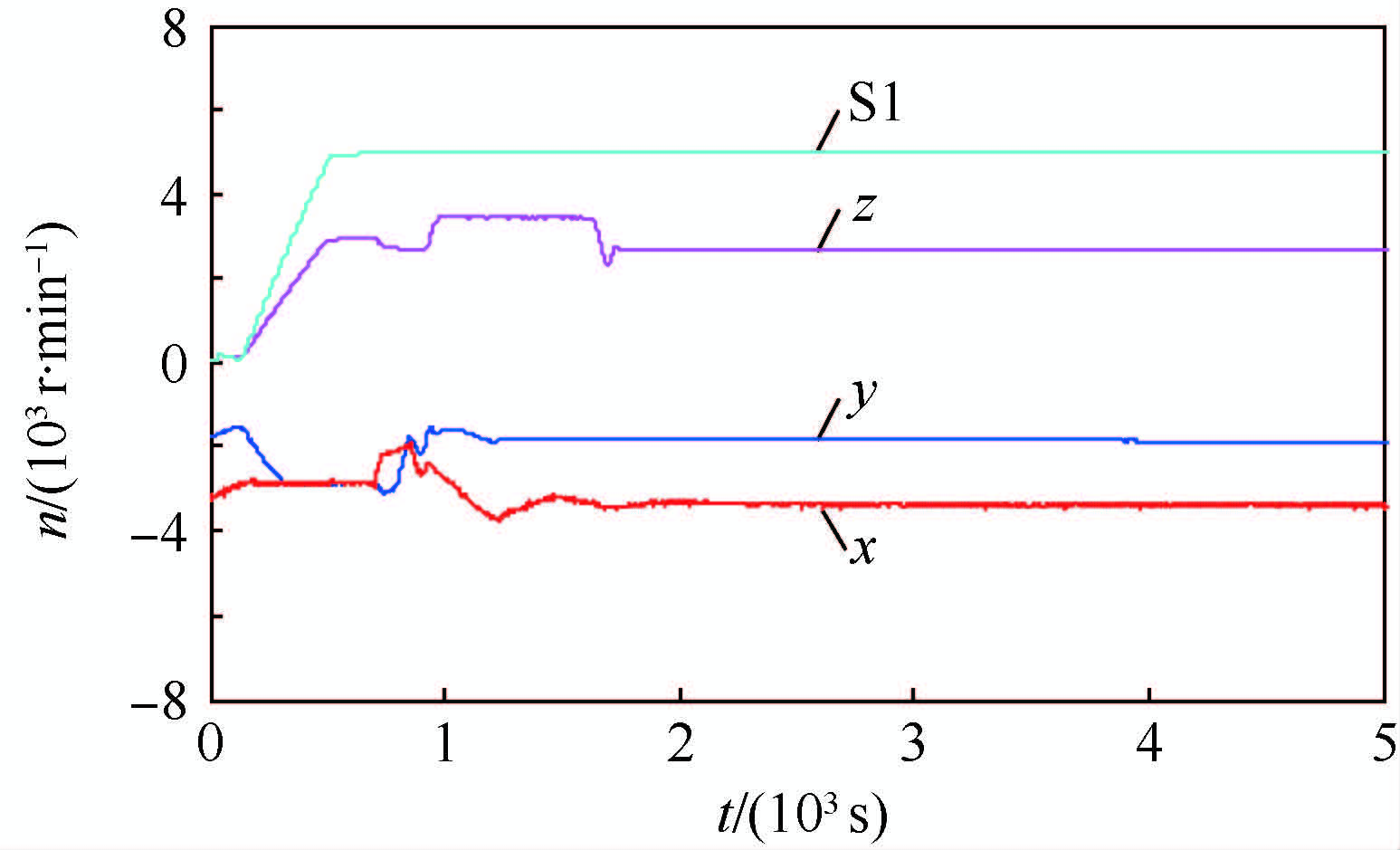
图 1和图 2为典型的过往半物理仿真试验数据。如图所示，x、y轴方向均有叠加噪声的近似常值的外力矩干扰引入，由于该外力矩(M)的持续引入，使反作用轮转速(n)沿某一方向持续上升，直至超出转速阈值,影响正常半物理仿真试验的有效进行。

图  1  典型过往仿真中外力矩引入

Figure  1.  Typical external torque introduction in previous simulations

下载: 全尺寸图片 幻灯片

图  2  典型过往仿真反作用轮轮速

Figure  2.  Typical reaction wheels’ speed in previous simulations

下载: 全尺寸图片 幻灯片

1.2   力矩测量系统输出误差计算

对于力矩测量系统输出偏差分析，可利用式(5)计算力矩测量系统实时输出与反作用轮实时转速差分力矩所得差值。

式中：M_err为力矩测量系统输出偏差；M_out为力矩测量系统输出值；J_wh为单轴反作用轮转动惯量；ω_now和ω_pre为当前时刻及上一采样时刻反作用轮转速;Δt采样间隔时间。

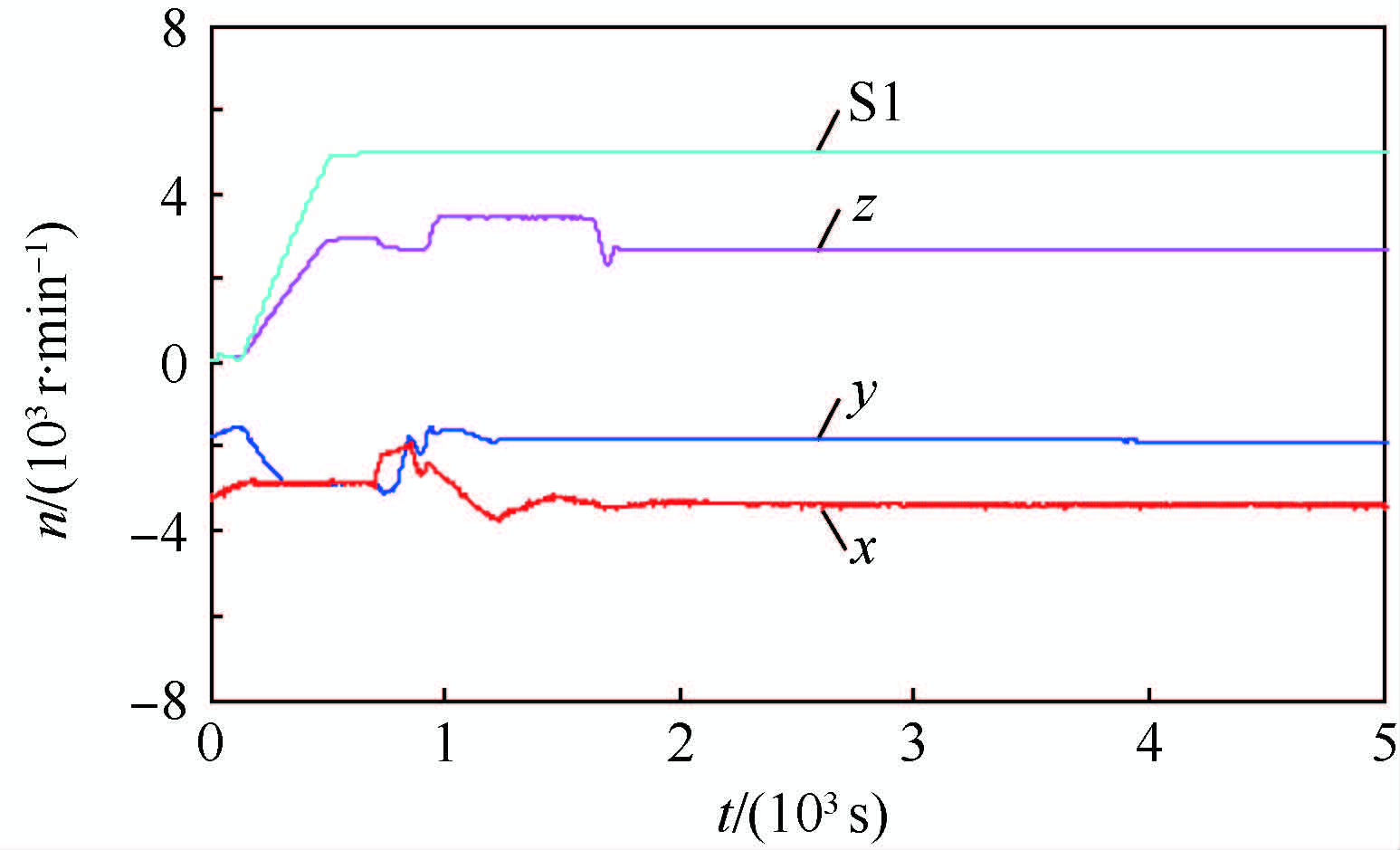
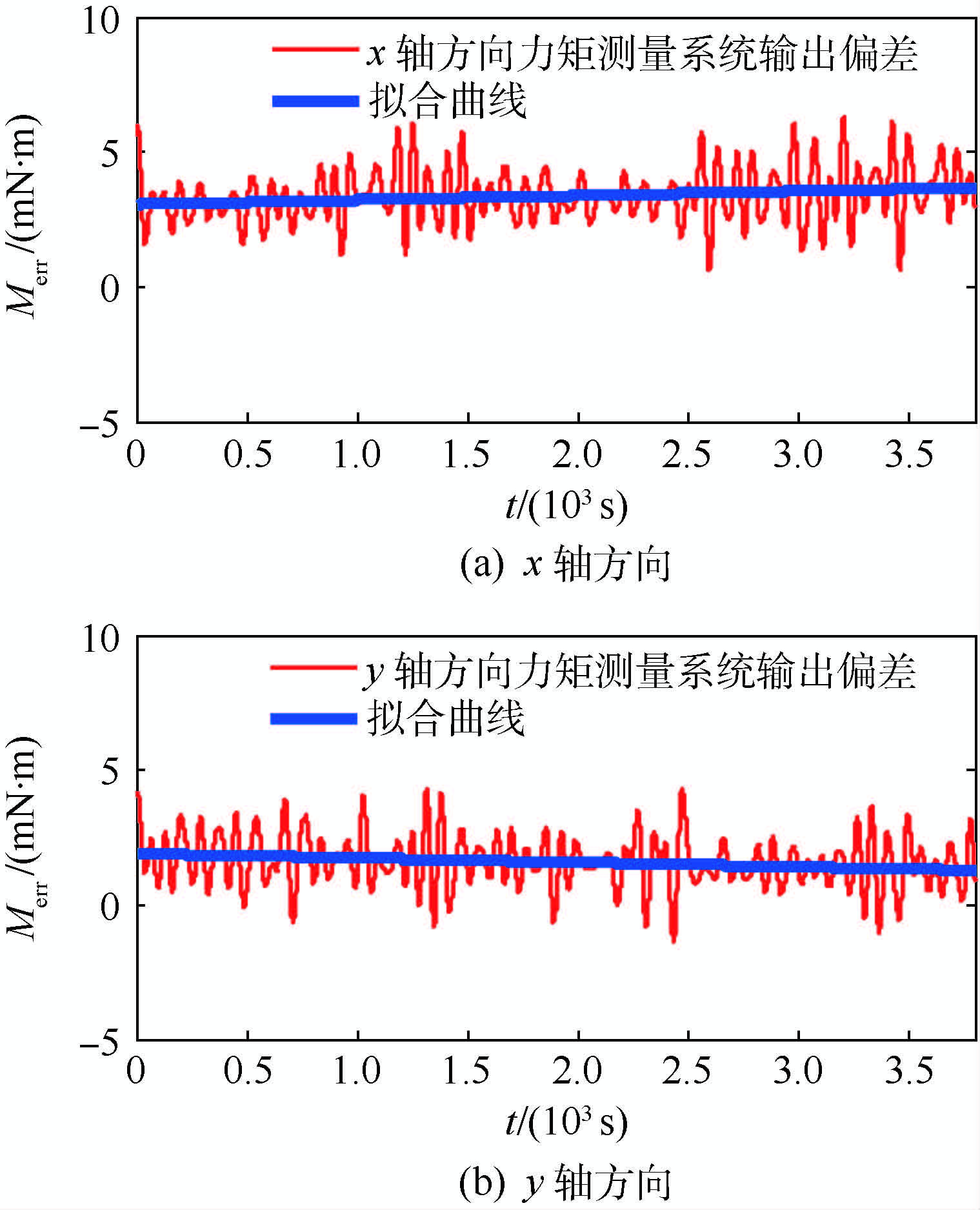
力矩测量系统输出偏差如图 3所示。

图  3  力矩测量系统输出偏差

Figure  3.  Output deviations in torque measuring system

下载: 全尺寸图片 幻灯片

图 1与图 3为同一时段卫星动力学模型外力矩引入及力矩测量系统输出误差数据。通过对图 1与图 3比较可知，2幅图直线拟合误差几乎相同。而所相差的噪声误差多为仿真过程模拟天上环境随机干扰叠加所致。因此，经分析可得，对力矩测量系统进行准确校准即可消除仿真过程中外力矩干扰。

1.3   力矩测量系统输出误差分析

试验所采用的反作用轮力矩测量系统主要由单轴高精度气浮轴承、高精度力传感器、信号前端处理器组成。系统利用高精度气浮轴承为反作用轮力矩测量提供一个微小力矩干扰环境，并利用高精度力传感器采集反作用轮输出力的大小乘以其到回转中心半径得到输出力矩测量信号。力矩测量信号通过信号前端处理器放大，被计算机采样，发送给姿态动力学模拟计算机，以实现控制闭环中反作用轮实时力矩引入。系统根据气浮台摩擦力矩，力传感器精度等因素，设定力矩测量精度为0.5 mN·m。

由图 3所示，力矩测量系统初始输出力矩误差(M_err)即已超出精度之外，且即使力矩误差在测量精度之内，由于半物理仿真对地稳定环节需持续较长时间，由式(6)将参与试验的反作用轮转动惯量代入，可知每小时反作用轮转速至多会产生440 r的转速漂移。显然，在对地稳定仿真环节长达1~2 d的长时间仿真下，会导致反作用轮转速漂移加剧。因此，在初始阶段与仿真过程中均需对测量系统进行实时校准。

式中：Δω 为一段时间内角速度变化量；t_p 为间隔时间。

2.   小波阈值滤波原理介绍

本文所采用的实时小波滤波方法以及小波滤波后的移动平均算法均使用了小波阈值滤波去噪的原理。小波降噪可以较好地保留原始信号，滤去试验中的噪声误差，从而较好地显示初始时刻及过程中测量系统产生偏差，以达到对系统准确校准的目的。小波滤波去噪过程可分为3步：

1) 离散小波变换。通过选择适当的小波基将信号f(t)分解为

式中：ψ_j,k为小波函数，参见式(8)，其构成一组正交基。

式中：a₀为尺度因子；b₀为平移因子，通常取a₀=2,b₀=1。

本文为满足实时性要求，基于Mallat算法^[11]对信号进行快速离散小波变换，并选取“DB6”小波，并进行5层分解。

2) 选择阈值，对小波系数进行阈值截断。

文献[12]提出了软阈值的消噪原理,参见式(9)，文献[13]提出了“rigrsure”为最佳软阈值选取方法。在此，小波去噪算法均选取软阈值及“rigrsure”选取方法。

式中：W为原小波系数；δ为阈值。

3) 对截断后的修正小波系数进行重构，得到去噪后信号。

3.   力矩测量系统校准

3.1   力矩测量系统初始阶段偏差补偿

图 4为力矩测量系统在30 min内的初始加电数据，由图可见初始输出偏差值(M_err)为伴有一定噪声的较大随机常值力矩偏差，且其初始时刻有较大输出振荡。通常使用的人为手动初始校准，由于力矩测量系统初始时刻较大的输出振荡及噪声影响，输出力矩值在人为校准后依然会与真实值存在偏差，使外力矩持续引入。并且人为初始校准方法也存在着需反复校准、无法判断力矩测量系统何时平稳输出等问题，给试验带来困扰。

图  4  力矩测量系统初始上电误差

Figure  4.  Initial power-up errors in torque measuring system

下载: 全尺寸图片 幻灯片

由实时小波滤波方法具有兼顾小波良好的去噪能力与实时性的优点，本文采用该方法对初始误差进行补偿，以使力矩测量系统初始状态准确校准。首先，借鉴文献[2, 14]中实时小波滤波参数选取，在试验中，采用滑动数据窗方法进行滑动滤波以保证实时性，选取数据窗大小为256。并且，为防止由小波滤波方法的边界干扰，采用对称数据窗的方法，将某一时刻采集数据对称添加于数据窗口中，使数据更新时，更新值在窗口中部。

同时，通过实时小波滤波方法，还可实现系统自动补偿校准，无需人为反复标定。而且，可根据补偿值在某一范围稳定时长，判断力矩测量系统是否稳定输出，以使仿真开始时，不会伴有较大的系统输出偏差。经多次采集力矩测量系统初始加电数据分析，本文采用时长为300 s，阈值为1 mN·m作为判断系统平稳输出标准。

图 5和图 6为典型的对力矩测量系统采用实时小波滤波方法进行初始校准后的试验结果。

图  5  小波初始校准外力矩引入

Figure  5.  External torque introduction based onwavelet initial calibration

下载: 全尺寸图片 幻灯片

图  6  小波初始校准反作用轮转速

Figure  6.  Reaction wheels’ speed based on wavelet initial calibration

下载: 全尺寸图片 幻灯片

由图 1、图 5及图 2、图 6比较可知，与经人为初始校准的半物理仿真过程相比，由实时小波滤波初始校准后的半物理仿真试验校准更为精确，仅存在仿真过程中测量精度范围内的些许外力矩偏差，因此外力矩引入较少，反作用轮转速上升较慢。

3.2   力矩测量系统仿真过程中偏差补偿

对仿真过程中系统输出偏差，本文基于反演法原理^[15]，并采用小波去噪后的均值滤波算法进行补偿。

反演法原理，即实时计算当前测量系统力矩输出偏差，并对偏差进行实时补偿。

而采用小波去噪后的均值滤波方法原因有二：第一，无法采用实时性较好的方法。首先，校准过程需实时采集的反作用轮转速叠加有较大的噪声干扰。这是因为闭环仿真中需人为叠加随机噪声以模拟天上环境，在反作用轮作用时，为保证卫星姿态稳定，这些噪声均会作用于反作用轮上，因此反作用轮转速存在较大振荡；再有，仿真试验环境实时性较差，试验采集到的实时轮速往往与力矩测量系统实时输出值具有1~2 s的误差。综上，若采用实时性较好的方法会使系统输出波动较大的力矩值，致使反作用轮转速剧烈振荡，甚至使卫星动力学模型失稳。第二，若直接使用移动平均算法进行输出误差补偿，需基于较大数据量进行平均，以滤去力矩系统引入的随机噪声，该方法不仅使校准的实时性减弱，也使实时系统校准的准确性大大降低。

因此，通过以上分析，在仿真过程中，本文实时采集力矩测量系统输出力矩值，及反作用轮实时转速，根据式(5)实时计算系统输出偏差值。而后取当前一段时间的偏差值经小波去噪后进行平均，将均值取反补偿于测量系统输出力矩值中，以实现对力矩测量系统仿真过程中的准确校准。为保证程序的通用性，在基于实时小波滤波方法的程序基础上，将均值数据长度选取为400，进行基于小波去噪的移动平均算法进行滤波。

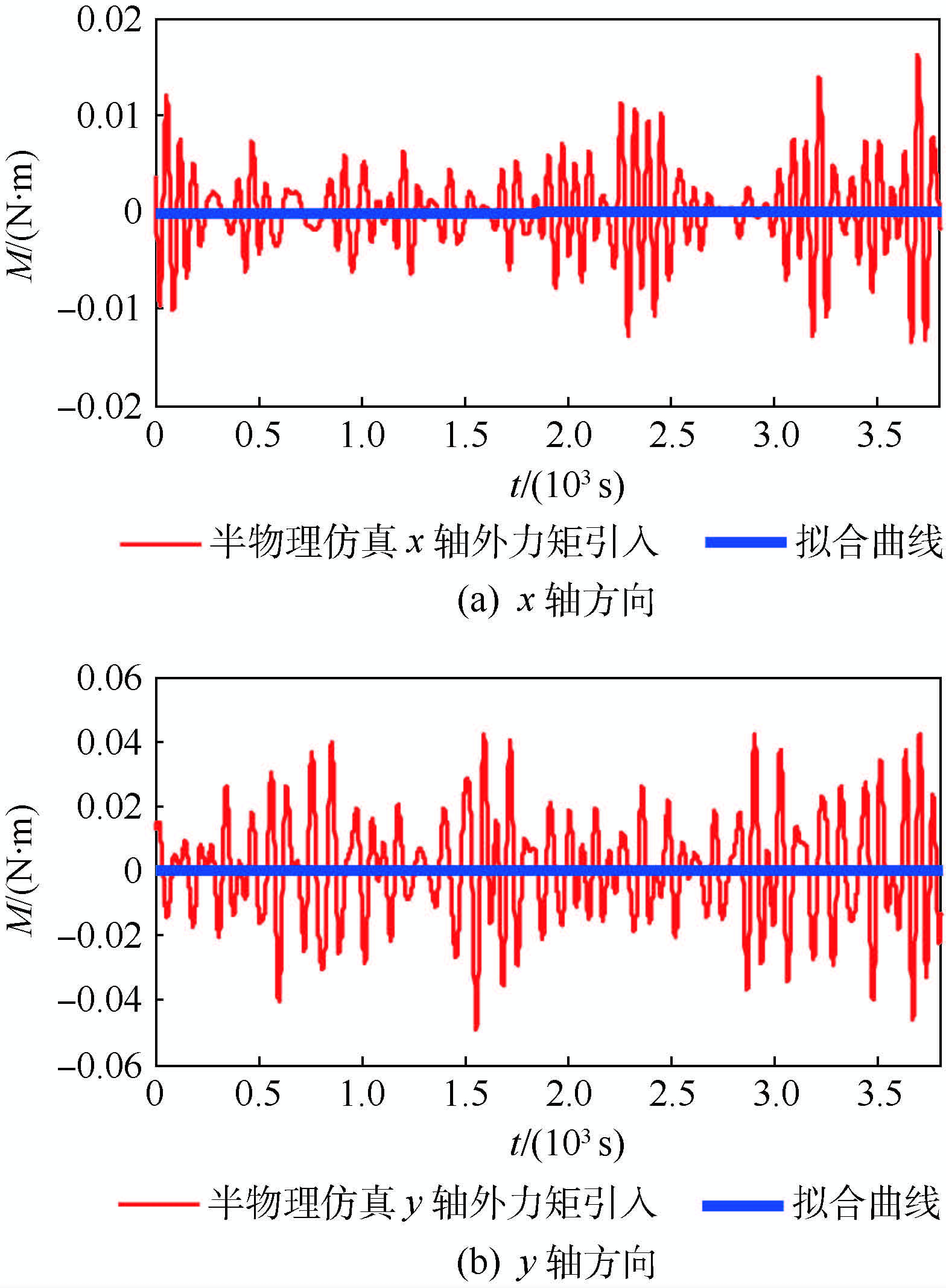
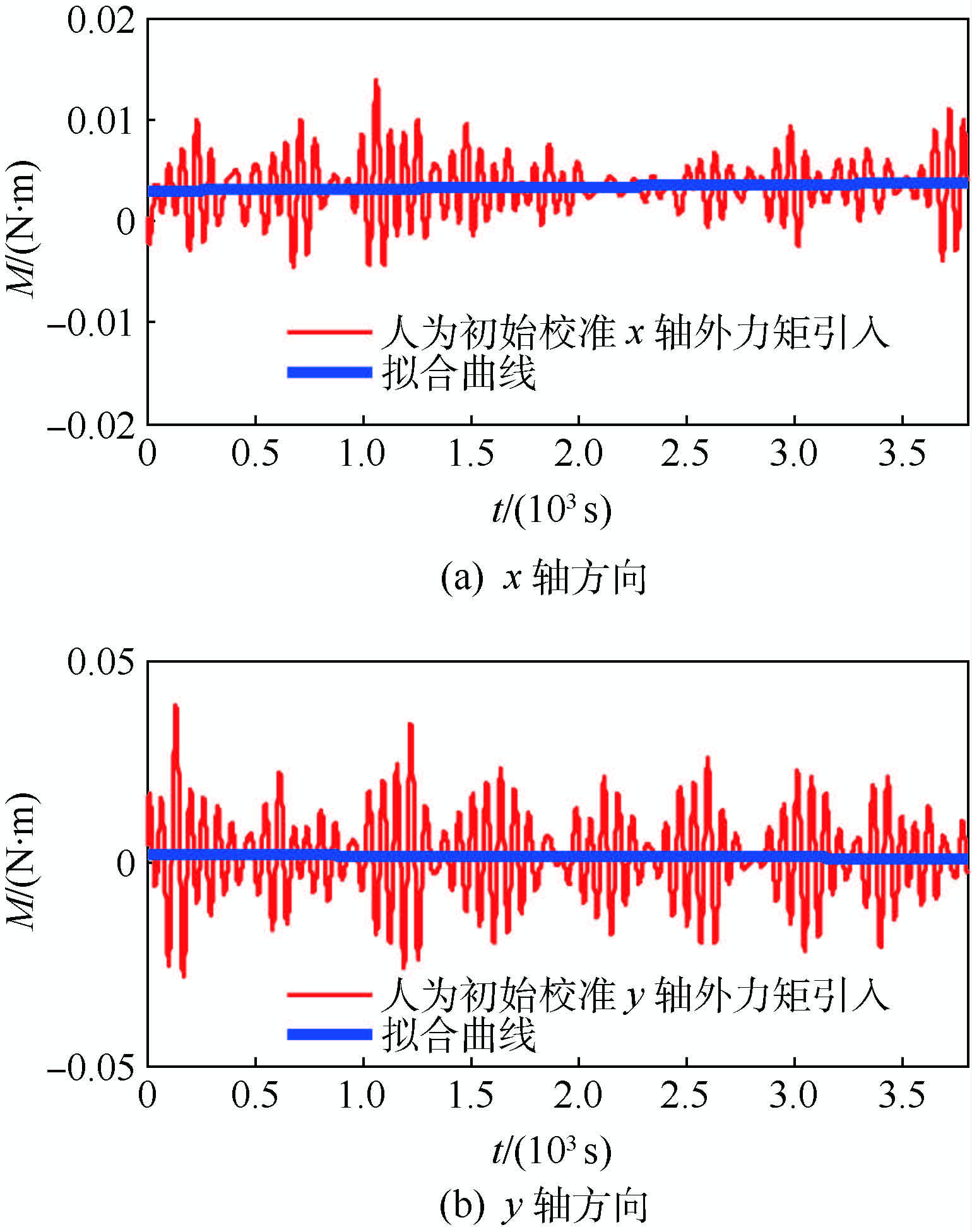
图 7和图 8为仿真过程中仅采用基于小波滤波的移动平均算法的仿真结果。如图所示，该方法抑制了仿真过程中伴随的外力矩引入，因而x、y轴反作用轮转速后期趋于平稳。虽然由于采集实时反作用轮转速导致仿真环境噪声量引入，使外力矩(M)振荡加剧叠加噪声有所增大。然而通过小波的良好去噪效果，噪声仍在工程可接受范围之内。但稍有不足的是，仅采用该方法时，由于力矩测量系统初始误差较大，使前期存在较大的外力矩引入，导致初始力矩补偿存在明显振荡，且反作用轮转速平稳后转速较标称转速有明显偏离。

图  7  基于小波去噪的移动平均滤波法外力矩引入

Figure  7.  External torque introduction based on moving averagefiltering method incorporated with wavelet de-noising

下载: 全尺寸图片 幻灯片

图  8  基于小波去噪的移动平均滤波法反作用轮转速

Figure  8.  Reaction wheels’ speed based on moving averagefiltering method incorporated with wavelet de-noising

下载: 全尺寸图片 幻灯片

3.3   半物理仿真试验结果分析

将3.1和3.2节提到的2种方法结合应用于半物理仿真试验中，补偿效果如图 9~图 11所示。经过较长时间试验运行，可以看出，在整个半物理仿真试验过程中，未有明显外力矩引入，实现了力矩测量系统的准确校准。因此，在卫星三轴对地稳定后，卫星姿态角和姿态角速度均几乎为0，反作用轮在标称转速值附近稳定运转，保证了半物理仿真试验的正常运行。

图  9  半物理仿真试验外力矩引入

Figure  9.  External torque introduction in semi-physical simulation experiment

下载: 全尺寸图片 幻灯片

图  10  半物理仿真试验反作用轮转速

Figure  10.  Reaction wheels’ speed in semi-physicalsimulation experiment

下载: 全尺寸图片 幻灯片

图  11  半物理仿真试验卫星姿态

Figure  11.  Satellite attitude in semi-physical simulation

下载: 全尺寸图片 幻灯片

4.   结 论

将反作用轮实时输出力矩引入半物理闭环仿真可使闭环仿真具有更好的实时性与真实性。但以往由于仿真闭环存在外力矩干扰，致使该闭环仿真方法无法有效应用。本文首先通过过往仿真试验数据分别计算试验中卫星动力学模型外力矩值与力矩测量系统输出偏差值，确定了力矩测量系统为仿真外力矩干扰源。而后针对力矩测量系统误差特性，使用实时小波滤波方法对力矩测量系统初始误差进行消除；基于反演法，并采用基于小波去噪的移动平均算法对仿真过程中误差引入进行补偿。试验结果表明，初始时刻，使用实时小波滤波方法进行校准相比于传统的人为手动校准其效果更为准确，方法易于操作，并且能够判断力矩测量系统输出是否平稳，以开始仿真试验；在仿真过程中，基于反演法原理，并采用基于小波去噪的移动平均算法可将试验过程中产生的外力矩干扰实时去除，并可抑制由于采集反作用轮转速而带来的仿真环境中的干扰引入力矩系统输出。经试验验证，结合2种方法应用于闭环仿真试验，可将力矩测量系统准确校准，将半物理仿真试验中外力矩干扰消除，并使反作用轮实时力矩值准确地引入仿真闭环，使这一更为优越的反作用轮闭环仿真新方法投入于半物理仿真试验中使用。