High-accuracy static aeroelastic analysis of fighter's transonic aileron efficiency and test flight verification
-
摘要:
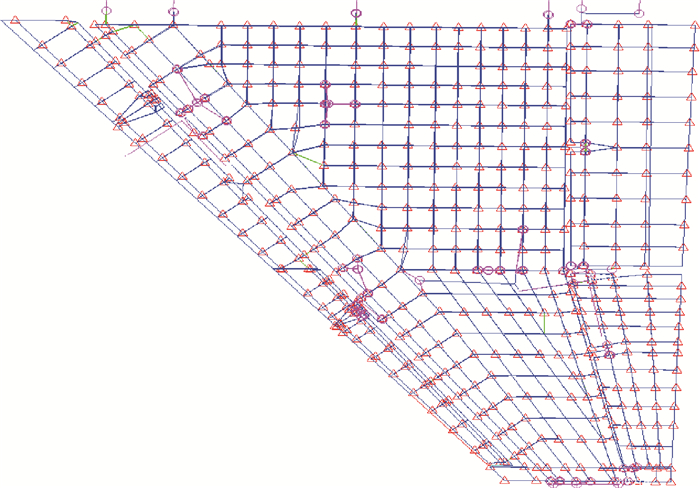
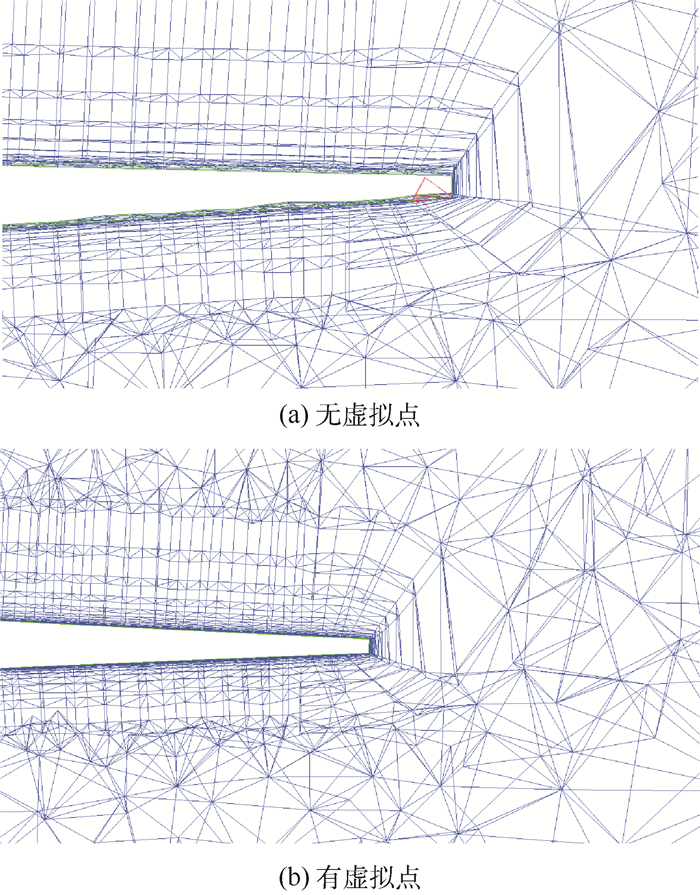
跨声速副翼效率一直是静弹分析领域的热点和难点问题之一。目前，基于计算流体力学（CFD）/计算结构动力学（CSD）耦合的高精度静弹分析方法用于此类问题时还存在网格变形鲁棒性以及分析结果缺乏有效验证等问题。针对上述问题，提出了基于虚拟网格及虚拟位移的网格变形方法，对于迭代中出现的非物理振荡、非一致收敛问题，采用了松弛迭代以及部件载荷综合残差收敛方法。基于上述方法，分析了某型战斗机的跨声速（
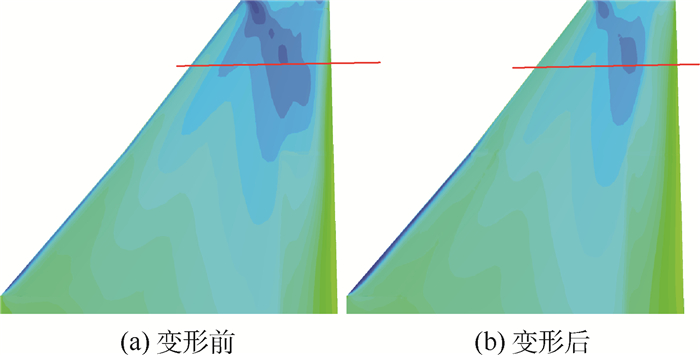
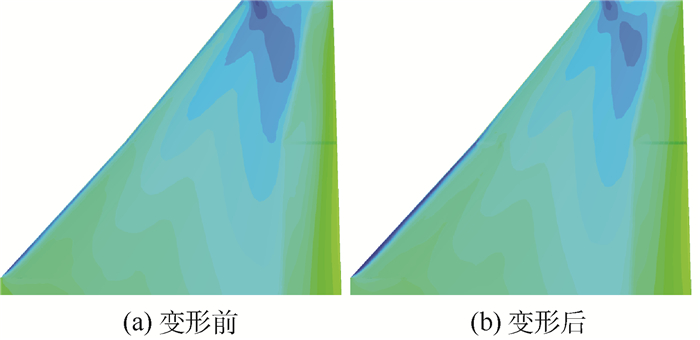
Ma =0.95）副翼效率，给出了静弹变形对翼面激波位置、激波强度、压力分布的影响以及副翼效率的弹性修正系数。为验证分析结果，开展了静弹试飞辨识，两者吻合良好，表明本文所提方法可以满足复杂构型跨声速副翼效率高精度静弹分析的需求，对于提高静弹工程设计能力具有重要意义。Abstract:The transonic aileron efficiency is a hotspot and difficulty in the field of static aeroelastic analysis. The computational fluid dynamics (CFD)/computational structural dynamics (CSD) interaction method can supply high-accuracy resolutions, but it still has problems of mesh deformation robustness and lack of verification. Aimed at the above issues, a new method of mesh deformation based on dummy grids and dummy deformation was developed, and for the problems of non-physical oscillation and non-uniformly convergence in the process of interaction, the lax iteration method and comprehensive residual criterions were used. Based on the methods, the transonic (
Ma =0.95) aileron efficiency of a fighter was analyzed, and the shock position/strength and the pressure distribution due to the static aeroelastic deformation were presented. The ration of elastic and rigid aileron efficiency was compared to the results of flight identification, which proves that the methods can meet the requirement of high-accuracy analysis for transonic static aeroelastic problems of control surfaces. The methods are of great significance for static aeroelastic engineering design capability enhancement. -
图 7 刚性气动力计算值与试验值的比较
Figure 7. Comparision of rigid aerodynamics between calculation and test values
图 9 机翼上表面变形前后压力分布比较 (δA=5°)
Figure 9. Comparison of pressure contour of wing's upper surface before and after deformation (δA=5°)
图 10 副翼剖面压力系数分布比较 (δA=5°)
Figure 10. Comparison of aileron's section pressure coefficient distribution (δA=5°)
图 11 机翼上表面变形前后压力分布比较 (δA=-5°)
Figure 11. Comparison of pressure contour of wing's upper surface before and after deformation (δA=-5°)
图 12 副翼剖面压力系数分布比较 (δA=-5°)
Figure 12. Comparison of aileron's section pressure coefficient distribution (δA=-5°)
-
[1] BOEHM B, FLICK P, SANDERS B, et al.Static aeroelastic response predictions of the active aeroelastic wing (AAW) flight research vehicle:AIAA-2001-1372[R].Reston:AIAA, 2001. [2] HEEG J, SPAIN C V, FLORANCE J R, et al.Experimental results from the active aeroelastic wing wind tunnel test program:AIAA-2005-2234[R].Reston:AIAA, 2005. [3] WISEMAN C D, SILVA W A, SPAIN C V, et al.Transonic-small-disturbance and linear analyses for the active aeroelastic wing program:AIAA-2005-1995[R].Reston:AIAA, 2005. [4] LEE D H, BALDELLI D H, LINDSLEY N J, et al.Static aeroelastic and open-loop aeroservoelastic analyses for the F/A-18 AAW aircraft:AIAA-2007-2135[R].Reston:AIAA, 2007. [5] 张伟伟, 高传强, 叶正寅.气动弹性计算中网格变形方法研究进展[J].航空学报, 2014, 35(2):303-319. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201402002.htmZHANG W W, GAO C Q, YE Z Y.Research progress on mesh deformation method in computational aeroelasticity[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(2):303-319(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201402002.htm [6] 张来平, 邓小刚, 张涵信.动网格生成技术及非定常计算方法进展综述[J].力学进展, 2010, 40(4):424-447. http://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201004006.htmZHANG L P, DENG X G, ZHANG H X.Reviews of moving grid generation techniques and numerical methods for unsteady flow[J].Advances in Mechanics, 2010, 40(4):424-447(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201004006.htm [7] PRANANTA B B, MEIJER J J.Transonic static aeroelastic simulations of fighter aircraft:NLR-TP-2003-187[R].Toronto:[s.n.], 2003. [8] FRANK R.Scattered data interpolation:Tests of some methods[J].Mathematics of Computation, 1982, 38(175):181-200. https://www.researchgate.net/publication/238834111_Scattered_Data_Interpolation_Tests_of_Some_Method [9] 林言中, 陈兵, 徐旭.径向基函数插值方法在动网格技术中的应用[J].计算物理, 2012, 29(2):191-197. http://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201202006.htmLIN Y Z, CHEN B, XU X.Radial basis function interpolation in moving mesh technique[J].Chinese Journal of Computational Physics, 2012, 29(2):191-197(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201202006.htm [10] 贾欢, 孙秦.基于径向基函数的动网格技术应用研究[J].机械科学与技术, 2013, 32(4):510-513. http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201304009.htmJIA H, SUN Q.Analyzing dynamic grid based on radial basis function[J].Mechanical Science and Technology for Aerospace Engineering, 2013, 32(4):510-513(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201304009.htm [11] ALLEN C B, RENDALL T C S.Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions:AIAA-2007-3804[R].Reston:AIAA, 2007. [12] SHENG C H, ALLEN C B.Efficient mesh deformation using radial basis functions on unstructured meshes[J].AIAA Journal, 2013, 51(3):707-720. doi: 10.2514/1.J052126 [13] RENDALL T C S, ALLEN C B.An efficient fluid-structure interpolation and mesh motion scheme for large aeroelastic simulations:AIAA-2008-6235[R].Reston:AIAA, 2008. [14] 王刚, 雷博琪, 叶正寅.一种基于径向基函数的非结构混合网格变形技术[J].西北工业大学学报, 2011, 29(5):784-788. http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201105031.htmWANG G, LEI B Q, YE Z Y.An efficient deformation technique for hybrid unstructured grid using radial basis functions[J].Journal of Northwestern Polytechnical University, 2011, 29(5):784-788(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201105031.htm [15] 谢亮, 徐敏, 张斌, 等.基于径向基函数的高效网格变形算法研究[J].振动与冲击, 2013, 32(10):141-145. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201310027.htmXIE L, XU M, ZHANG B, et al.Space points reduction in grid deforming method based on radial basis functions[J].Journal of Vibration and Shock, 2013, 32(10):141-145(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201310027.htm -
下载:
点击查看大图
计量
- 文章访问数: 1048
- HTML全文浏览量: 156
- PDF下载量: 642
- 被引次数: 0
