-
摘要:
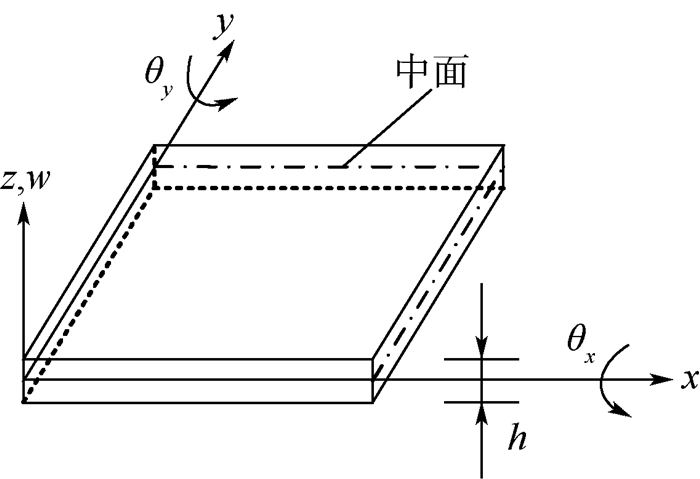
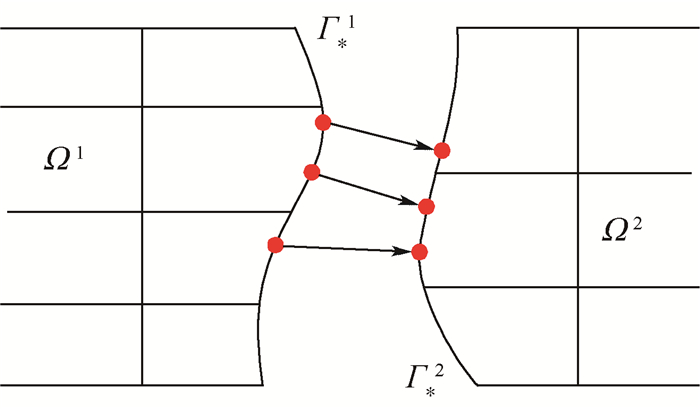
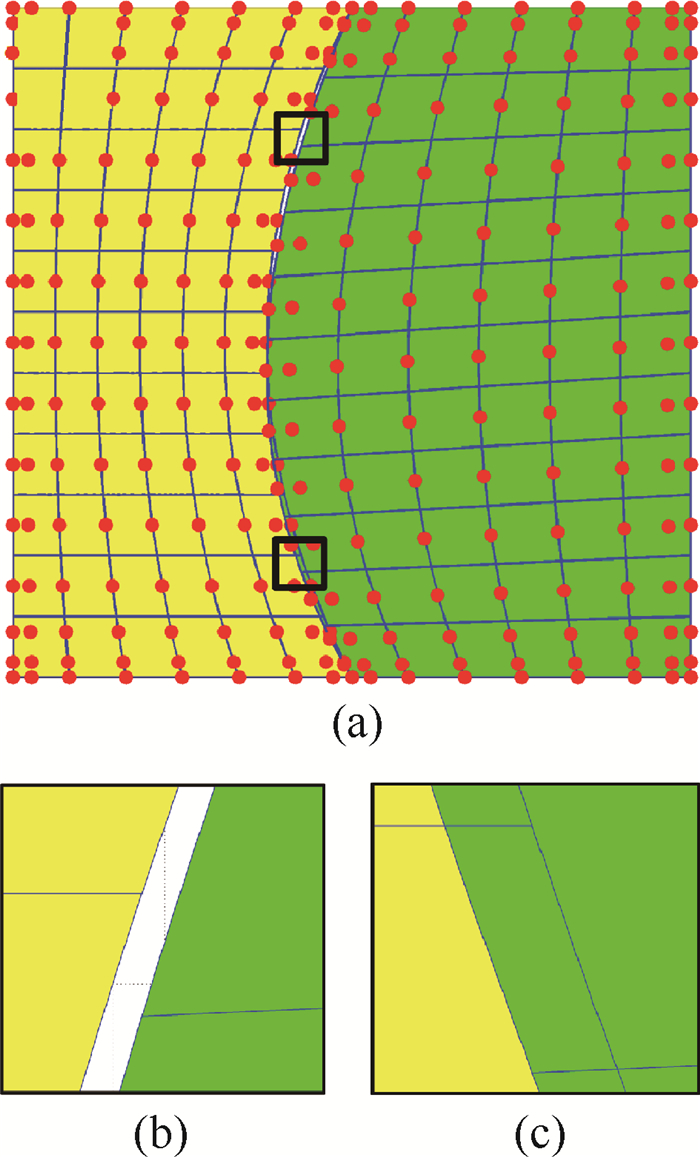
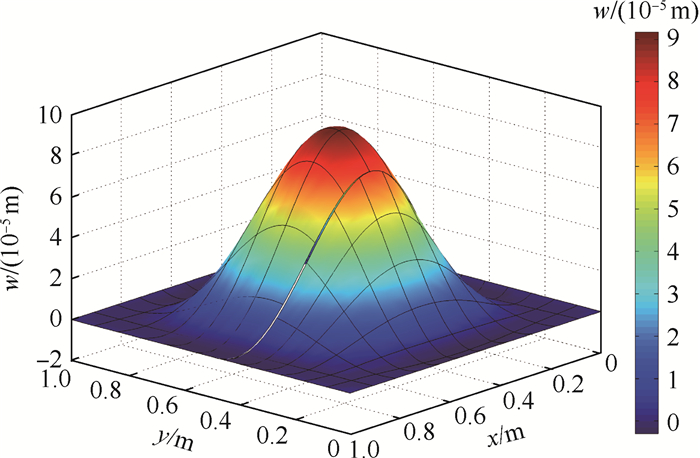
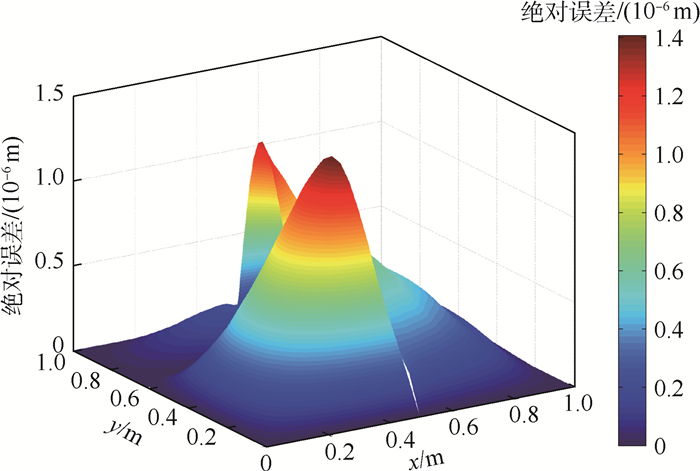
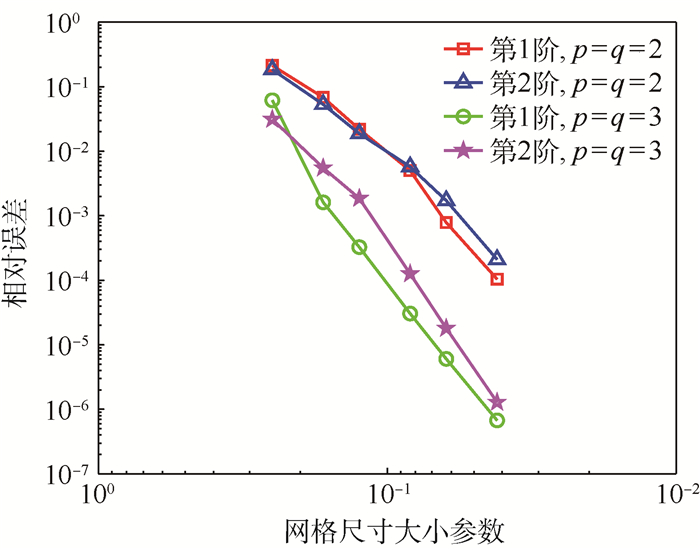
等几何分析（IGA）中非均匀有理B样条（NURBS）被同时用作计算机辅助设计（CAD）中的建模工具以及有限元分析（FEA）中的逼近函数。NURBS模型中常见的缝隙和重叠问题使得分析变得困难。基于Mindlin板理论，对含有缝隙与重叠部分的NURBS模型进行等几何分析，采用Nitsche方法处理模型交界面上的非协调问题，并通过标准数值仿真算例的计算结果与解析解对比验证方法的可行性。研究结果表明：基于Nitsche的等几何方法可以用来对含局部缝隙与重叠特征的非协调Mindlin板模型进行分析；NURBS次数越高，等几何分析计算结果越精确，并且收敛速度越快。
-
关键词:
- 等几何分析 (IGA) /
- Mindlin板 /
- 非协调 /
- Nitsche方法 /
- 缝隙与重叠
Abstract:In the frame of isogeometric analysis (IGA), non-uniform rational B-spline (NURBS) serves as both the description of geometries in computer aided design (CAD) and the shape function in finite element analysis (FEA). The common problems of gap and overlapping in NURBS models increase the difficulty of analysis. Based on Mindlin plate theory, the NURBS plate models with gap and overlapping were analyzed by IGA method. The Nitsche method was employed to solve non-conforming problem along models' interfaces. The simulation results of benchmark problem obtained by IGA method were compared with analytical solutions to verify the validity of the presented method. It is demonstrated that Nitsche based IGA method can be used to analyze non-conforming Mindlin plate models with local gap and overlapping feature. Higher NURBS polynomial degrees will produce more accurate IGA results and faster convergence.
-
Key words:
- isogeometric analysis (IGA) /
- Mindlin plate /
- non-conforming /
- Nitsche method /
- gap and overlapping
-
图 8 不同次数下的非协调方板前10阶频率相对误差
Figure 8. Relative errors of first ten mode frequencies of non-conforming square plate with different polynomial degrees
图 9 不同次数下的第1阶和第2阶非协调方板频率参数收敛
Figure 9. Convergence of first two mode frequency parameters of non-conforming square plate with different polynomial degrees
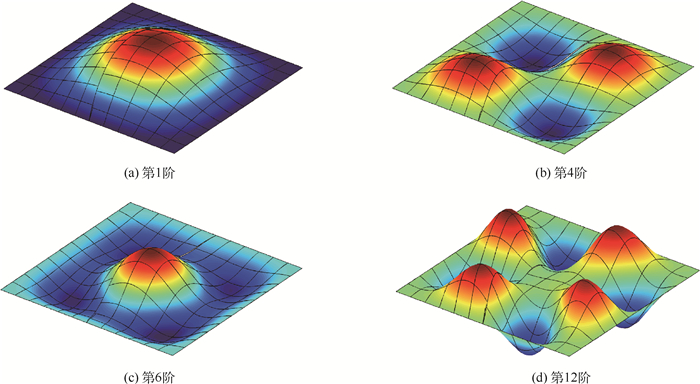
表 1 非协调固支方板频率参数
Table 1. Frequency parameters of non-conforming clamped square plate
模态阶数 h/l=0.1 h/l=0.2 等几何分析 Liew等[16] 等几何分析 Liew等[16] 1 3.297 0 3.295 4 2.688 4 2.687 5 2 6.270 5 6.285 8 4.680 9 4.690 7 3 6.304 7 6.285 8 4.702 1 4.690 7 4 8.810 6 8.809 8 6.298 6 6.298 5 5 10.377 1 10.378 8 7.174 3 7.176 7 6 10.484 3 10.477 8 7.278 3 7.275 9 7 12.539 4 12.552 9 8.507 0 8.515 5 8 12.570 0 12.552 9 8.522 7 8.515 5 9 15.296 0 15.291 8 10.008 9 10.012 6 10 15.305 7 15.291 8 10.017 7 10.012 6 
下载: 导出CSV
-
[1] HUGHES T J R, COTTRELL J A, BAZILEVS Y.Isogeometric analysis:CAD, finite elements, NURBS, exact geometry and mesh refinement[J].Computer Methods in Applied Mechanics & Engineering, 2005, 194(s39-41):4135-4195. https://www.researchgate.net/publication/51992200_Isogeometric_analysis_CAD_finite_elements_NURBS_exact_geometry_and_mesh_refinement [2] HESCH C, BETSCH P.Isogeometric analysis and domain decomposition methods[J].Computer Methods in Applied Mechanics & Engineering, 2012, 213(1):104-112. http://www.sciencedirect.com/science/article/pii/S0045782511003823 [3] 祝雪峰. 复杂曲面非协调等几何分析及相关造型方法[D]. 大连: 大连理工大学, 2012.ZHU X F.Nonconforming isogeometric analysis for geometrically complex CAD surfaces and geometric modeling[D].Dalian:Dalian University of Technology, 2012(in Chinese). [4] NGUYEN V P, KERFRIDEN P, BRINO M, et al.Nitsche's method for two and three dimensional NURBS patch coupling[J].Computational Mechanics, 2014, 53(6):1-20. doi: 10.1007/s00466-013-0955-3 [5] APOSTOLATOS A, SCHMIDT R, WVCHNER R, et al.A Nitsche-type formulation and comparison of the most common domain decomposition methods in isogeometric analysis[J].International Journal for Numerical Methods in Engineering, 2014, 97(7):473-504. doi: 10.1002/nme.v97.7 [6] RUESS M, SCHILLINGER D, ÖZCAN A I, et al.Weak coupling for isogeometric analysis of non-matching and trimmed multi-patch geometries[J].Computer Methods in Applied Mechanics & Engineering, 2014, 269(2):46-71. https://www.researchgate.net/publication/259095237_Weak_coupling_for_isogeometric_analysis_of_non-matching_and_trimmed_multi-patch_geometries [7] GUO Y, RUESS M.Nitsche's method for a coupling of isogeometric thin shells and blended shell structures[J].Computer Methods in Applied Mechanics & Engineering, 2015, 284:881-905. https://www.researchgate.net/publication/273179241_Nitsche%27s_method_for_a_coupling_of_isogeometric_thin_shells_and_blended_shell_structures [8] DU X X, ZHAO G, WANG W.Nitsche method for isogeometric analysis of Reissner-Mindlin plate with non-conforming multi-patches[J].Computer Aided Geometric Design, 2015(s35-36):121-136. http://www.sciencedirect.com/science/article/pii/S016783961500028X [9] NITSCHE J.Vber ein variationsprinzip zur l sung von dirichlet-problemen bei verwendung von teilräumen, die keinen randbedingungen unterworfen sind[J].Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 1971, 36:9-15. doi: 10.1007/BF02995904 [10] SANDERS J D, LAURSEN T A, PUSO M A.A Nitsche embedded mesh method[J].Computational Mechanics, 2012, 49(2):243-257. doi: 10.1007/s00466-011-0641-2 [11] PIEGL L, TILLER W.The NURBS book[M].2nd ed.New York:Springer, 1997. [12] XU G, MOURRAIN B, DUVIGNEAU R, et al.Parameterization of computational domain in isogeometric analysis:Methods and comparison[J].Computer Methods in Applied Mechanics & Engineering, 2011, 200(s23-24):2021-2031. https://www.researchgate.net/publication/251502906_Parameterization_of_computational_domain_in_isogeometric_analysis_Methods_and_comparison [13] ZIENKIEWICZ O C, TAYLOR R L.The finite element method for solid and structural mechanics[M].6th ed.Singapore:Butterworth-Heinemann, 2005:323-336. [14] CHINOSI C, LOVADINA C.Numerical analysis of some mixed finite element methods for Reissner-Mindlin plates[J].Computational Mechanics, 1995, 16(1):36-44. doi: 10.1007/BF00369883 [15] KIENDL J, AURICCHIO F, VEIGA L B D, et al.Isogeometric collocation methods for the Reissner-Mindlin plate problem[J].Computer Methods in Applied Mechanics & Engineering, 2015, 284:489-507. https://www.researchgate.net/publication/268037995_Isogeometric_collocation_methods_for_the_Reissner-Mindlin_plate_problem [16] LIEW K M, XIANG Y, KITIPORNCHAI S.Transverse vibration of thick rectangular plates-I.Comprehensive sets of boundary conditions[J].Computers & Structures, 1993, 49(1):1-29. http://www.sciencedirect.com/science/article/pii/004579499390122T -
下载:
点击查看大图
计量
- 文章访问数: 1133
- HTML全文浏览量: 124
- PDF下载量: 617
- 被引次数: 0
