-
摘要:
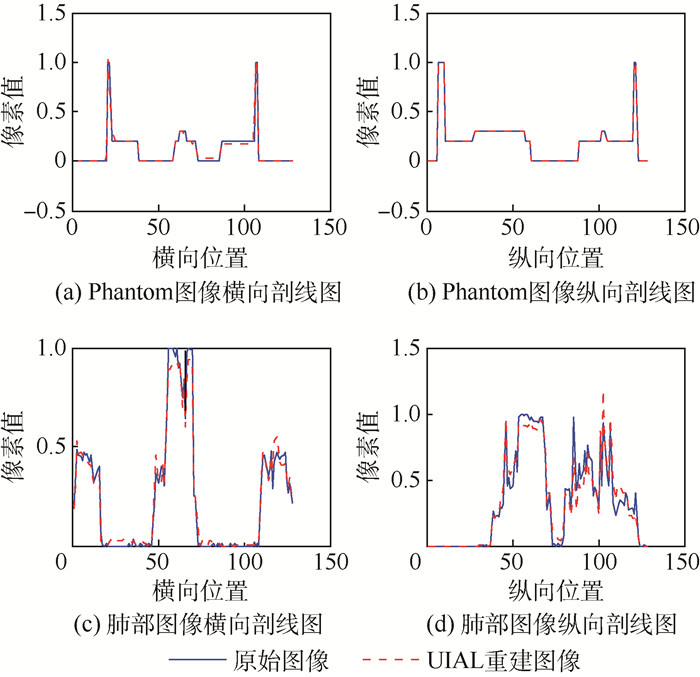
为了提升不完全角度计算机断层成像（CT）图像的重建精度和重建效率，研究了有限角度和稀疏角度下的CT图像重建问题，提出新的全变差最小化目标函数，通过将上一步迭代重建的图像作为反馈加入到新的迭代之中，不断更新目标函数的已知项。在算法求解时，采用增广Lagrangian罚函数方法，将约束问题非约束化，并将之转化为等价的3个子问题，通过在交替方向上求解子问题来获得优化问题的最优解。实验结果表明，该算法重建出的图像信息完整，细节清晰，重建精度高，与Split Bregman算法相比，本文算法结果的相对均方误差可下降42.1%~98.5%，条纹指标可下降42.8%~98.5%。
-
关键词:
- 计算机断层成像 (CT) /
- 图像重建 /
- 压缩感知 /
- 全变差正则化 /
- 增广Lagrangian方法
Abstract:To improve the accuracy and efficiency of few-view computed tomography (CT) image reconstruction, CT image reconstruction is studied from limited view and sparse view, and a novel objective function of total variation norm is proposed. According to the newly-developed objective function, the next iteration is based on the information acquired in the previous one, through which the updated sparse representation model is achieved at each iteration. Additionally, the constrained optimization problem is converted to unconstrained optimization one by adopting the augmented Lagrangian method. Then it can be equally expressed by three sub-problems which can be solved by the alternating minimization scheme. The experimental results using the proposed strategy show that it can attain higher quality CT images which possess integral information, clear detail and high precision. Furthermore, the relative root mean square error can be reduced by 42.1%-98.5% and the streak indicator 42.8%-98.5%, compared with those using Split Bregman-based algorithm.
-
图 2 有限角度下3种算法的重建图像
Figure 2. Reconstruction images of three algorithms in limited view
图 3 有限角度下重建图像与原始图像的像素比较
Figure 3. Pixel comparison of reconstruction images with original images in limited view
图 5 稀疏角度下重建图像与原始图像的像素比较
Figure 5. Pixel comparison of reconstruction images with original images in sparse view
表 1 有限角度下不同重建算法的重建结果
Table 1. Reconstruction results of different reconstruction algorithms in limited view
重建算法 Phantom 肺部 上腹部 肝部 RRSME SI 重建时间/s RRSME SI 重建时间/s RRSME SI 重建时间/s RRSME SI 重建时间/s FBP 0.77 14.41 1.18 0.74 10.76 1.89 0.77 12.99 5.24 0.76 13.55 1.49 SpBr 0.48 10.41 155.28 0.41 8.13 149.06 0.41 9.90 202.54 0.37 10.69 201.22 UIAL 0.06 1.54 29.22 0.17 3.81 29.69 0.13 3.78 48.62 0.14 4.80 44.27 
下载: 导出CSV
表 2 稀疏角度下不同重建算法重建结果
Table 2. Reconstruction results of different reconstruction algorithms in sparse view
重建算法 Phantom 肺部 上腹部 肝部 RRSME SI 重建时间/s RRSME SI 重建时间/s RRSME SI 重建时间/s RRSME SI 重建时间/s FBP 0.38 12.13 1.19 0.28 9.47 1.29 0.19 8.87 1.52 0.26 12.49 1.73 SpBr 0.20 6.15 148.19 0.19 6.43 129.84 0.10 5.08 178.15 0.20 9.66 183.95 UIAL 0.003 0.09 23.60 0.11 3.68 24.06 0.05 2.38 28.02 0.07 3.17 17.49
下载: 导出CSV
-
[1] 闫镔, 李磊.CT图像重建算法[M].北京:科学出版社, 2014:97-112.YAN B, LI L.CT image reconstruction algorithm[M].Beijing:Science Press, 2014:97-112(in Chinese). [2] CANDES E, ROMBERG J, TAO T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory, 2006, 52(2):489-509. doi: 10.1109/TIT.2005.862083 [3] HASHEMI S, BEHESHTI S, GILL P R, et al.Accelerated compressed sensing based CT image reconstruction[J].Computational & Mathematical Methods in Medicine, 2015:16797. http://europepmc.org/articles/PMC4489012 [4] TROPP J A, WRIGHT S J.Computational methods for sparse solution of linear inverse problems[J].Proceedings of the IEEE, 2010, 98(6):948-958. doi: 10.1109/JPROC.2010.2044010 [5] WANG Y, YANG J, YIN W, et al.A new alternating minimization algorithm for total variation image reconstruction[J].SIAM Journal on Imaging Sciences, 2008, 1(3):248-272. doi: 10.1137/080724265 [6] ZHU Z, WAHID K, BABYN P, et al.Improved compressed sensing-based algorithm for sparse-view CT image reconstruction[J].Computational & Mathematical Methods in Medicine, 2013(18):84-104. https://www.researchgate.net/profile/Paul_Babyn/publication/236255367_Improved_Compressed_Sensing-Based_Algorithm_for_Sparse-View_CT_Image_Reconstruction/links/00b7d53aadf055ea90000000.pdf?inViewer=true&pdfJsDownload=true&disableCoverPage=true&origin=publication_detail [7] 邓露珍, 冯鹏, 陈绵毅, 等.一种基于Contourlet变换与分裂Bregman方法的CT图像重建算法[J].CT理论与应用研究, 2014, 23(5):751-759. http://www.cnki.com.cn/Article/CJFDTOTAL-CTLL201405004.htmDENG L Z, FENG P, CHEN M Y, et al.An CT image reconstruction algorithm based on Contourlet transform and Split Bregman methods[J].CT Theory and Application Research, 2014, 23(5):751-759(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-CTLL201405004.htm [8] NIEN H, FESSLER J A.Fast X-ray CT image reconstruction using a linearized augmented Lagrangian method with ordered subsets[J].IEEE Transactions on Medical Imaging, 2014, 34(2):388-399. https://arxiv.org/abs/1402.4381 [9] NIEN H, FESSLER J.Relaxed linearized algorithms for faster X-Ray CT image reconstruction[J].IEEE Transactions on Medical Imaging, 2016, 35(4):1090-1098. doi: 10.1109/TMI.2015.2508780 [10] ZHANG H, HAN H, LIANG Z R, et al.Extracting information from previous full-dose CT scan for knowledge-based Bayesian reconstruction of current low-dose CT images[J].IEEE Transactions on Medical Imaging, 2016, 35(6):860-870. http://europepmc.org/abstract/MED/26561284 [11] CHEN G J, TANG J, LENG S.Prior image constrained compressed sensing (PICCS):A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets[J].Medical Physics, 2008, 35(2):660-663. doi: 10.1118/1.2836423 [12] 袁亚湘.非线性优化计算方法[M].北京:科学出版社, 2008:158-173.YUAN Y X.Nonlinear optimization calculating method[M].Beijing:Science Press, 2008:158-173(in Chinese). [13] LI C B.An efficient algorithm for total variation regularization with applications to the single pixel camera and compressed sensing[D].Houston, TX:Rice University, 2009:18-31. [14] XIE S L, GUAN C T, HUANG W M, et al.Fast TV MR image reconstruction using variable splitting and accelerated alternating direction method with adaptive restart[C]//2015 IEEE International Conference.Piscataway, NJ:IEEE Press, 2015:1085-1088. [15] PEACEMAN D W, RACHFORD H H.The numerical solution of parabolic and elliptic differential equations[J].Journal of the Society for Industrial & Applied Mathematics, 2006, 3(1):28-41. doi: 10.1137/0103003 [16] BARZILAI J, BORWEIN J M.Two-point step size gradient methods[J].IMA Journal of Numerical Analysis, 1988, 8(1):141-148. doi: 10.1093/imanum/8.1.141 [17] GOLDSTEIN T, OSHER S.The split Bregman method for L1-regularized problems[J].SIAM Journal on Imaging Sciences, 2009, 2(2):323-343. doi: 10.1137/080725891 [18] SIDDON R L.Fast calculation of the exact radiological path for a three-dimensional CT array[J].Medical Physics, 1985, 12(2):252-255. doi: 10.1118/1.595715 [19] HESTENES M R.Multiplier and gradient methods[J].Journal of Optimization Theory & Applications, 1969, 4(5):303-320. doi: 10.1007/BF00927673 -
下载:
点击查看大图
计量
- 文章访问数: 1238
- HTML全文浏览量: 193
- PDF下载量: 684
- 被引次数: 0
