-
摘要:
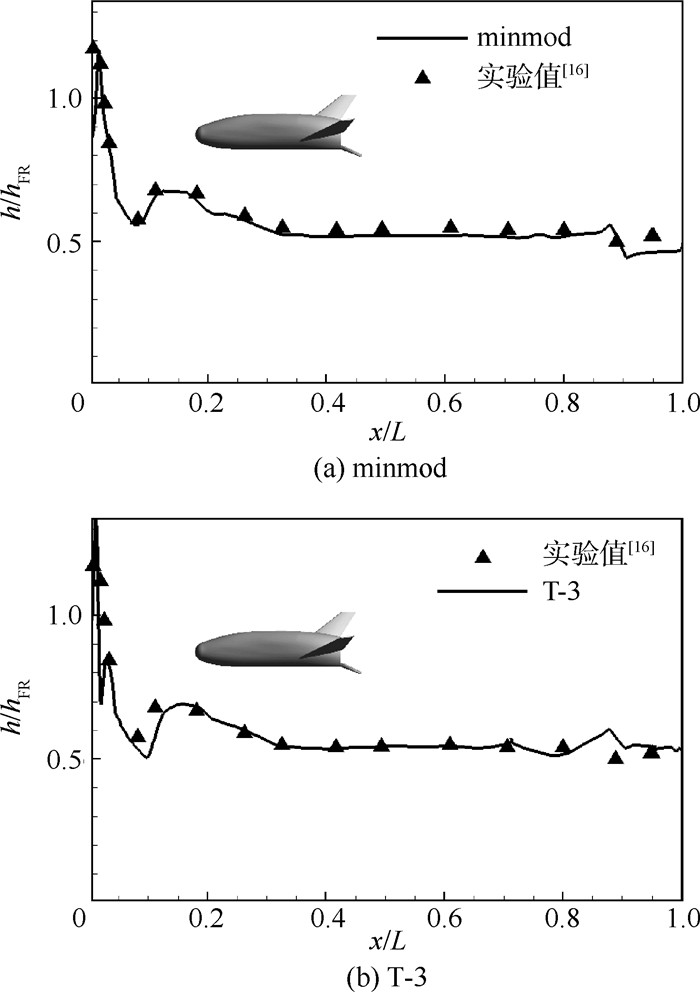
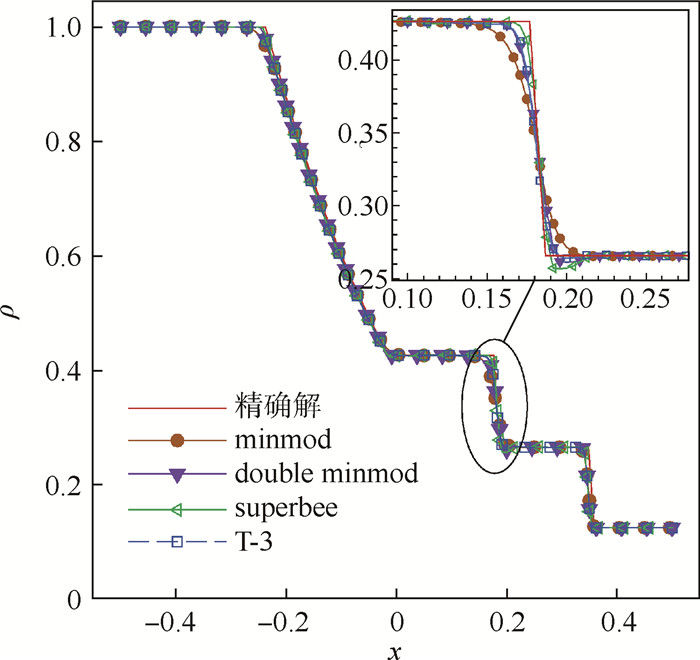
在计算流体力学（CFD）方法中，限制技术是影响计算精度和计算稳定性的重要因素，目前应用较广的经典二阶总变差衰减（TVD）限制器虽能较好地满足计算要求，但性能差异大且分辨率和耗散的性能间并未得到良好权衡。对一种新型的三阶TVD插值限制器（T-3限制器）进行了研究并将其与3种经典限制器进行对比。首先通过一维黎曼问题，得出T-3限制器兼顾较高间断分辨率和良好稳定性的特点；接着通过高超声速双锥绕流和X-33外形飞行器的数值实验，得到T-3限制器具有刻画复杂流动的能力以及较优的气动热计算性能。
-
关键词:
- 限制器 /
- 计算流体力学 (CFD) /
- 激波 /
- 双锥绕流 /
- 气动热
Abstract:For numerical scheme in computational fluid dynamics (CFD), limiter technology is an important factor affecting computational accuracy and stability. Although the present classical second-order total variation diminishing (TVD) limiters with a wide application can well satisfy the computing requirements, its performance not only largely differs but also cannot be properly weighted between resolution and dissipation. Therefore, a new third-order TVD interpolation limiter (T-3 limiter) has been studied and compared with three classical limiters. First, through one-dimensional Riemann problem, it has been found that T-3 limiter is simultaneously characterized by both high intermittent resolution and excellent stability; then, by numerical simulation of hypersonic flow over a double-cone body and X-33 configuration, it has been found that T-3 limiter boasts the capability of portraying complex flow and good aerothermodynamic calculation performance.
-
Key words:
- limiter /
- computational fluid dynamics (CFD) /
- shocks /
- double-cone disturbance flow /
- aerothermodynamic
-
图 4 壁面压强沿母线分布曲线
Figure 4. Distribution curves of wall surface pressure along generating line
图 5 40°迎角下对称面等马赫线图和壁面压强云图
Figure 5. Mach contours in symmetry plane and wall surface pressure contours at α=40°
图 7 迎风区子午线热流分布与实验值的对比
Figure 7. Comparison between windward centerline heat flow distribution and experimental data
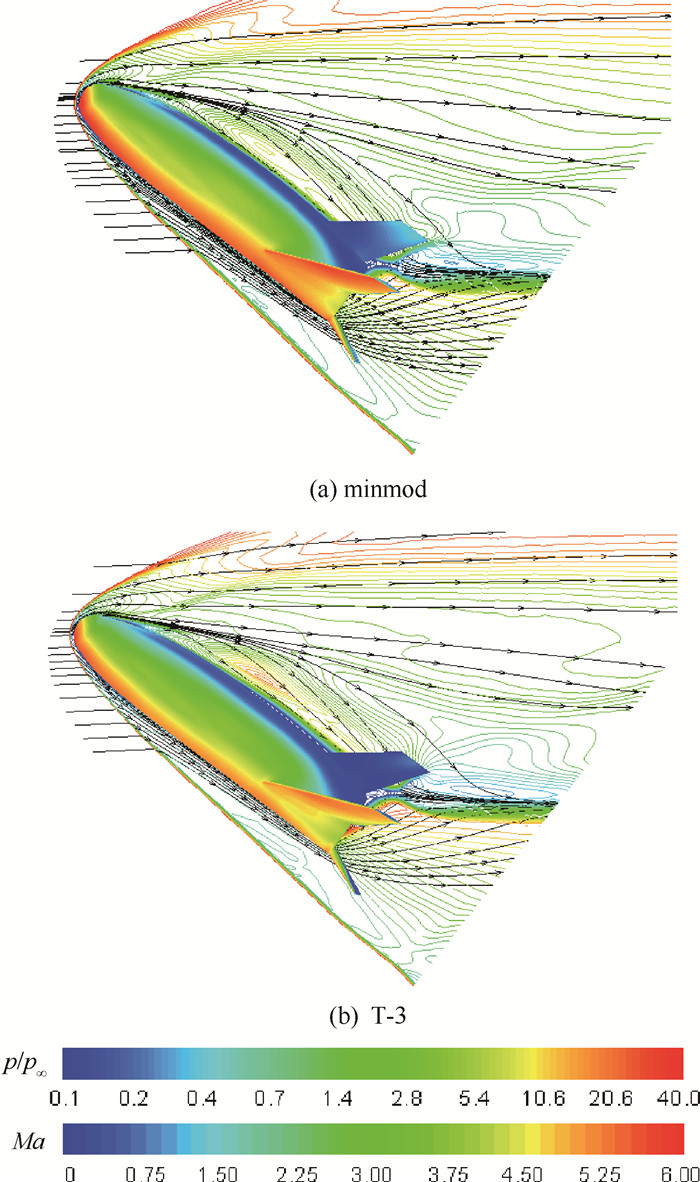
表 1 分离点、再附点、分离区长度的计算结果
Table 1. Calculated separation position, reattachment position and separation zone length
限制器 x/L 分离点 再附点 分离区长度 minmod 0.597 5 1.103 5 0.506 double minmod 0.565 8 1.164 1 0.598 superbee 0.505 0 1.151 1 0.646 T-3 0.449 1 1.095 0 0.646 
下载: 导出CSV
表 2 壁面压强峰值计算结果
Table 2. Calculated results of wall surface pressure peak
限制器 峰值位置 (x/L) 位置误差/% 压强峰值 (p/p∞) 峰值误差/% 实验 1.424 5 104.698 minmod 1.358 5 4.633 0 94.307 9.925 double minmod 1.429 6 0.358 0 94.689 9.560 superbee 1.437 5 0.913 0 107.886 3.045 T-3 1.498 5 1.825 0 102.831 1.783
下载: 导出CSV
-
[1] HARTEN A.High resolution schemes for hyperbolic conservation laws[J].Journal of Computational Physics, 1983, 49(3):357-393. doi: 10.1016/0021-9991(83)90136-5 [2] LEER B V.Towards the ultimate conservative difference scheme V:A second-order sequal to Godunov's method[J].Journal of Computational Physics, 1979, 32(1):101-136. doi: 10.1016/0021-9991(79)90145-1 [3] HARTEN A, ENGQUIST B, OSHER S, et al.Unifomrly high-order accurate essentially non-oscillatory schemes[J].Journal of Computational Physics, 1987, 71(2):231-303. doi: 10.1016/0021-9991(87)90031-3 [4] LIU X D, OSHER S, TONY C.Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics, 1994, 115(1):200-212. doi: 10.1006/jcph.1994.1187 [5] SWEBY P K.High resolution schemes using flux limiters for hyperbolic conservational laws[J].SIAM Journal of Numerical Analysis, 1984, 21(5):995-1011. doi: 10.1137/0721062 [6] VENKATAKRISHMAN V.Convergence to steady state solutions of the Euler equations on unstructured grids with limiters[J].Journal of Computational Physics, 1995, 118(1):120-130. doi: 10.1006/jcph.1995.1084 [7] 屈峰, 阎超, 于剑, 等.高精度激波捕捉格式的性能分析[J].北京航空航天大学学报, 2014, 40(8):1085-1089. http://bhxb.buaa.edu.cn/CN/abstract/abstract13000.shtmlQU F, YAN C, YU J, et al.Assessment of shock capturing methods for numerical simulations of compressible turbulence with shock waves[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(8):1085-1089(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13000.shtml [8] YEE H C, KLOPFER G H, MINTAGNE J L.High resolution shock capturing schemes for inviscid and viscous hypersonic flows[J].Journal Computational Physics, 1990, 83(1):31-61. https://www.researchgate.net/publication/222485266_High-resolution_shock-capturing_schemes_for_inviscid_and_viscous_hypersonic_flows [9] SPEKREIJSE S.Multigrid solution of monotone second order discretization of hypersonic conservation laws[J].Mathematics of Computational, 1987, 49(179):135-155. doi: 10.1090/S0025-5718-1987-0890258-9 [10] YOON S H, KIM K H, KIM C.Multi-dimensional limiting process for the three-dimensional flow physics analyses[J].Journal of Computational Physics, 2008, 227(12):6001-6043. doi: 10.1016/j.jcp.2008.02.012 [11] KIM K H, KIM C.Accurate, efficient and monotonic numetical methods for multi-dimensional compressible flows, Part Ⅱ:Multi-dimensional limiting process[J].Journal of Computational Physics, 2005, 208(2):570-615. doi: 10.1016/j.jcp.2005.02.022 [12] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社, 2006:123-127.YAN C.Computational fluid dynamic's methods and applications[M].Beijing:Beihang University Press, 2006:123-127(in Chinese). [13] 孙迪, 阎超, 于剑, 等.高精度多维限制器的性能分析[J].北京航空航天大学学报, 2015, 41(3):437-442. http://bhxb.buaa.edu.cn/CN/abstract/abstract13185.shtmlSUN D, YAN C, YU J, et al.Performance analysis of high accurate multi-dimensional limiting process[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3):437-442(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13185.shtml [14] WRIGHT M J, SINHA K, OLEJNICZAK J, et al.Numerical and experimental investigation of double-cone shock interactions[J].AIAA Journal, 2000, 38(12):2268-2276. doi: 10.2514/2.918 [15] BRIAN R H, THOMAS J H, SCOTT A B, et al.X-33 computational aeroheating predictions and comparisons with experimental data[J].Journal of Spacecraft and Rockets, 1999, 38(5):658-669. https://www.researchgate.net/publication/2291000_X-33_Computational_Aeroheating_Predictions_and_Comparisons_with_Experimental_Data [16] BERRY S A, HORVATH T J, HOLLIS B R, et al.X-33 hypersonic boundary-layer transition[J].Journal of Spacecraft and Rockets, 2001, 38(5):646-657. doi: 10.2514/2.3750 -
下载:
点击查看大图
计量
- 文章访问数: 1095
- HTML全文浏览量: 159
- PDF下载量: 644
- 被引次数: 0
