NFFD控制点分布对气动外形优化的影响

马明生; 唐静; 李彬; 周桂宇

doi:10.13700/j.bh.1001-5965.2016.0277

NFFD控制点分布对气动外形优化的影响

doi: 10.13700/j.bh.1001-5965.2016.0277

马明生^{1, 2, ,},
唐静¹,
李彬²,
周桂宇²

1.
西北工业大学航空学院, 西安 71007
2.
中国空气动力研究与发展中心计算空气动力研究所, 绵阳 621000

详细信息

作者简介:
马明生, 男, 博士, 研究员, 博士生导师。主要研究方向:飞行器气动总体设计

唐静, 男, 博士研究生。主要研究方向:飞行器气动外形优化设计、非结构网格技术

李彬, 男, 博士。主要研究方向:飞行器气动外形优化设计、外挂物分离投放数值模拟

通讯作者:
马明生, E-mail:ma_mingsheng@sina.cn

中图分类号: V221⁺.3;TB553
计量
- 文章访问数: 860
- HTML全文浏览量: 145
- PDF下载量: 665
- 被引次数: 0
出版历程
- 收稿日期: 2016-04-11
- 录用日期: 2016-05-20
- 网络出版日期: 2017-04-20

Effects of NFFD control points distribution on aerodynamic shape optimization

MA Mingsheng^{1, 2
, ,},
TANG Jing¹,
LI Bin²,
ZHOU Guiyu²

1.
School of Aeronautics, Northwestern Polytechnical University, Xi'an 71007
2.
Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China

More Information

Corresponding author: MA Mingsheng, E-mail:ma_mingsheng@sina.cn

摘要

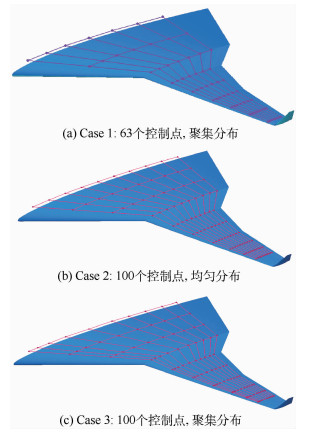
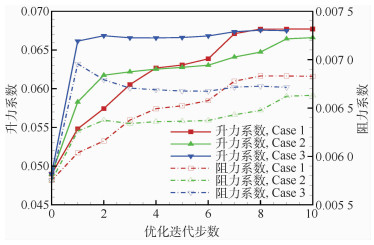
摘要:
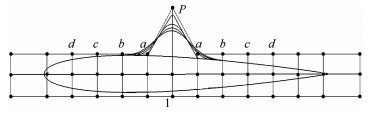
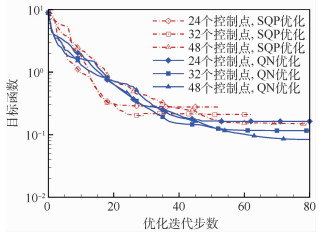
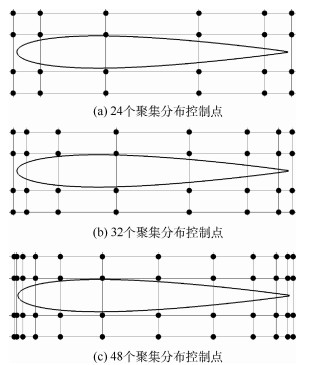
基于非均匀有理B样条的自由型面变形（NFFD）技术具有对变形对象普适性和控制点影响区域局部性的特点，广泛应用于气动外形优化。本文通过扩展控制体和合理布置外侧控制点，实现了NFFD技术在参数化曲面并改变曲面形状时，同步变形控制体内的表面网格和空间网格，并从理论上保证了控制体边界内外的网格协调。基于离散伴随方法求取梯度，分别采用拟牛顿（QN）法和序列二次规划（SQP）优化方法，通过从初始翼型NACA0012到标准翼型EH1590的反设计，研究了NFFD控制点数量和分布对设计结果的影响。在某飞翼标模单点全机升阻比优化应用中，改进控制点分布后获得了更高的升阻比，收敛速度显著提高。
- 气动优化 /
- 反设计 /
- 自由型面变形 /
- 网格变形 /
- 控制点分布 /
- 翼型 /
- 飞翼
Abstract:
The NURBS based free-form deformation (NFFD), which is universal for representation of object geometry, and whose control point influence zone is local for geometry deformation, is used widely for aerodynamic shape optimization. By extending the control volume and locating the outer control points appropriately, NFFD is used to parameterize the surface, deform the surface grid and volume grid in one single process. The grid cells both inside and outside control volume are preserved consistent theoretically after shape deformation. With the gradient of object function calculated by discrete adjoint method, both the quasi-Newton (QN) and sequential quadratic programming (SQP) optimization techniques are applied to inverse airfoil design from the initial airfoil, NACA0012, to the standard flying-wing airfoil, EH1590. The effects of the number and distribution of control points on optimization result are discussed. In the case of the lift-to-drag ratio optimization for a whole aircraft with flying-wing in a single design state, the convergence speed is improved obviously and higher lift-to-drag ratio is obtained by improving the distribution of control points.
- aerodynamic optimization /
- inverse design /
- free-form deformation /
- grid deformation /
- control points distribution /
- airfoil /
- flying-wing

HTML全文

图 1 变形前后控制体和翼型

Figure 1. Control volume and airfoil before and after deformation

下载: 全尺寸图片幻灯片

图 2 不同基函数次数时翼型变形

Figure 2. Airfoil deformation of different basis function degrees

下载: 全尺寸图片幻灯片

图 3 修改后的控制体和变形后的翼型

Figure 3. Modified control volume and deformed airfoil

下载: 全尺寸图片幻灯片

图 4 二维NFFD控制点和其定义的控制曲面

Figure 4. 2D control points and control surface of NFFD

下载: 全尺寸图片幻灯片

图 5 同时参数化物面和变形空间网格的控制体

Figure 5. Control volume for both shape parameterization and space grid deformation

下载: 全尺寸图片幻灯片

图 6 NFFD变形空间网格

Figure 6. Space grid deformation by NFFD

下载: 全尺寸图片幻灯片

图 7 IDWF变形空间网格

Figure 7. Space grid deformation by IDWF

下载: 全尺寸图片幻灯片

图 8 初始翼型和3种均匀分布控制点

Figure 8. Initial airfoil and three types of uniformly distributed control points

下载: 全尺寸图片幻灯片

图 9 控制点均匀分布时目标函数收敛历程

Figure 9. Convergence history of objective function with uniformly distributed control points

下载: 全尺寸图片幻灯片

图 10 控制点均匀分布时反设计翼型比较

Figure 10. Comparison of inversely designed airfoils with uniformly distributed control points

下载: 全尺寸图片幻灯片

图 11 第1步各控制点的目标函数梯度

Figure 11. Objective function gradient of control points at the first step

下载: 全尺寸图片幻灯片

图 12 初始翼型和3种聚集分布控制点

Figure 12. Initial airfoil and three types of aggregated distributed control points

下载: 全尺寸图片幻灯片

图 13 采用QN法和SQP方法的不同控制点目标函数收敛历程

Figure 13. Convergence history of objective function based on different control points by QN and SQP methods

下载: 全尺寸图片幻灯片

图 14 控制点均匀和聚集分布时反设计翼型比较

Figure 14. Comparison of inversely designed airfoils between uniformly and aggregated distributed control points

下载: 全尺寸图片幻灯片

图 15 飞翼优化改进前后的控制点及其分布

Figure 15. Control points and distribution before and after flying-wing optimization

下载: 全尺寸图片幻灯片

图 16 升阻比和相对容积比收敛历程

Figure 16. Convergence history of lift-to-drag ratio and volume ratio

下载: 全尺寸图片幻灯片

图 17 升力和阻力系数收敛历程

Figure 17. Convergence history of lift and drag coefficients

下载: 全尺寸图片幻灯片

图 18 优化后不同展向剖面几何形状和压力分布比较

Figure 18. Comparison of wing section shapes and pressure distribution at different span location after optimization

下载: 全尺寸图片幻灯片

参考文献(23)

[1]	BARRETT T R, BRESSLOFF N W, KEANE A J.Airfoil shape design and optimization using multifidelity analysis and embedded inverse design[J].AIAA Journal, 2006, 44(9):2051-2060. doi: 10.2514/1.18766
[2]	靳军, 刘波, 曹志鹏, 等.基于NURBS的三维轴流压气机叶片的几何型面优化研究[J].航空动力学报, 2005, 20(4):625-629. http://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200504017.htm JIN J, LIU B, CAO Z P, et al.Investigation of 3D axial flow compressor blade shape optimization based on NURBS[J].Journal of Aerospace Power, 2005, 20(4):625-629(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200504017.htm
[3]	马晓永, 范召林, 吴文华, 等.基于NURBS方法的机翼气动外形优化[J].航空学报, 2011, 32(9):1616-1621. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201109009.htm MA X Y, FAN Z L, WU W H, et al.Aerodynamic shape optimization for wing based on NURBS[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(9):1616-1621(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201109009.htm
[4]	卜月鹏, 宋文萍, 韩忠华, 等.基于CST参数化方法的翼型气动优化设计[J].西北工业大学学报, 2013, 31(5):829-836. http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201305032.htm BU Y P, SONG W P, HAN Z H, et al.Aerodynamic optimization design of airfoil based on CST parameterization method[J].Journal of Northwestern Polytechnical University, 2013, 31(5):829-836(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201305032.htm
[5]	李静, 高正红, 黄江涛, 等.基于CST参数化方法气动优化设计研究[J].空气动力学学报, 2012, 30(4):443-449. http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201305032.htm LI J, GAO Z H, HUANG J T, et al.Aerodynamic optimization system based on CST technique[J].Acta Aerodynamica Sinica, 2012, 30(4):443-449(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201305032.htm
[6]	王迅, 蔡晋生, 屈崑, 等.基于改进CST参数化方法和转捩模型的翼型优化设计[J].航空学报, 2015, 36(2):449-461. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201502005.htm WANG X, CAI J S, QU K, et al.Airfoil optimization based on improved CST parametric method and transition model[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(2):449-461(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201502005.htm
[7]	陈颂, 白俊强, 孙智伟, 等.基于DFFD技术的翼型气动优化设计[J].航空学报, 2014, 35(3):695-705. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201403010.htm CHEN S, BAI J Q, SUN Z W, et al.Aerodynamic optimization design of airfoil using DFFD technique[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3):695-705(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201403010.htm
[8]	AMOIRALIS E I, NIKOLOS I K.Freeform deformation versus B-spline representation in inverse airfoil design[J].Journal of Computing and Information Science in Engineering, 2008, 8(2):1-13.
[9]	李彬, 邓有奇, 唐静, 等.基于三维非结构网格的离散型伴随方法[J].航空学报, 2014, 35(3):674-686. http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201302019.htm LI B, DENG Y Q, TANG J, et al.Discrete adjoint method for 3D on unstructured grid[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3):674-686(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201302019.htm
[10]	王丹, 白俊强, 黄江涛.FFD方法在气动优化设计中的应用[J].中国科学:物理学力学天文学, 2014, 44(3):267-277. http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201403006.htm WANG D, BAI J Q, HUANG J T.The application of FFD method in aerodynamic optimization design[J].Scientia Sinica:Physica, Mechanica & Astronomica, 2014, 44(3):267-277(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201403006.htm
[11]	王元元, 张彬乾, 郭兆电, 等.基于FFD技术的大型运输机上翘后体气动优化设计[J].航空学报, 2013, 34(8):1806-1814. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201308007.htm WANG Y Y, ZHANG B Q, GUO Z D, et al.Aerodynamic optimization design for large upswept afterbody of transport aircraft based on FFD technology[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(8):1806-1814(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201308007.htm
[12]	黄江涛, 高正红, 白俊强, 等.基于任意空间属性FFD技术的融合式翼稍小翼稳健型气动优化设计[J].航空学报, 2013, 34(1):37-46. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201301004.htm HUANG J T, GAO Z H, BAI J Q, et al.Study of robust winglet design based on arbitrary space shape FFD technique[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(1):37-46(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201301004.htm
[13]	RONZHEIMER A, HEPPERLE M, BREZILLON J, et al.Aerodynamic optimal engine integration for a business jet configuration:AIAA-2012-1841[R].Reston:AIAA, 2012.
[14]	LI J, GAO Z H, HUANG J T, et al.Aerodynamic design optimization of nacelle/pylon position on an aircraft[J].Chinese Journal of Aeronautics, 2013, 26(4):850-857. doi: 10.1016/j.cja.2013.04.052
[15]	王婧超, 李立州, 岳珠峰.自由网格变形技术在涡轮叶片多学科设计优化过程中的应用[J].飞机设计, 2006, 27(3):40-43. http://www.cnki.com.cn/Article/CJFDTOTAL-FJSJ200603008.htm WANG J C, LI L Z, YUE Z F.Free-form deformation application in multidisciplinary design optimization procedure of turbine blades[J].Aircraft Design, 2006, 27(3):40-43(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-FJSJ200603008.htm
[16]	KENWAY G K W, KENNEDY G J.A CAD-free approach to high-fidelity aerostructural optimization:AIAA-2010-9231[R].Reston:AIAA, 2010.
[17]	唐静, 邓有奇, 马明生, 等.飞翼气动优化中参数化和网格变形技术[J].航空学报, 2015, 36(5):1480-1490. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201505011.htm TANG J, DENG Y Q, MA M S, et al.Parametrization and grid deformation techniques for flying-wing aerodynamic optimization[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(5):1480-1490(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201505011.htm
[18]	LYU Z, MARTINS J R R A.RANS-based aerodynamic shape optimization of a blended-wing-body aircraft:AIAA-2013-2586[R].Reston:AIAA, 2013.
[19]	SEDERBERG T W, PARRY S R.Free-form deformation of solid geometric models[J].ACM Siggraph Computer Graphics, 1986, 20(4):151-160. doi: 10.1145/15886
[20]	LAMOUSIN H J, WAGGENSPACK W N.NURBS-based free-form deformations[J].Computer Graphics and Applications, 1994, 14(6):59-65. doi: 10.1109/38.329096
[21]	YAMAZAKI W, MOUTON S, CARRIER G.Efficient design optimization by physics-based direct manipulation free-form deformation:AIAA-2008-5953[R].Reston:AIAA, 2008.
[22]	FARIN G.Curves and surfaces for computer aided geometry design-A practical guide[M].5th ed.New York:Academic Press, 2002.
[23]	PANIER E R, TITS A L.On combining feasibility, descent and superlinear convergence in inequality constrained optimization[J].Math Programming, 1993, 59(1):261-276.