-
摘要:
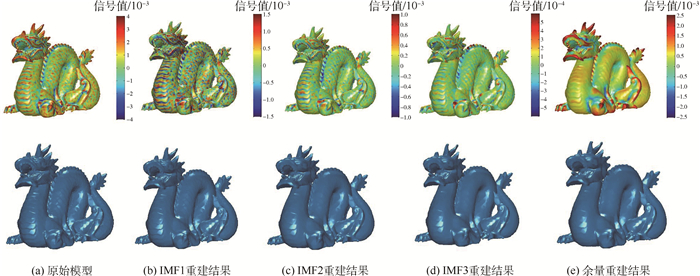
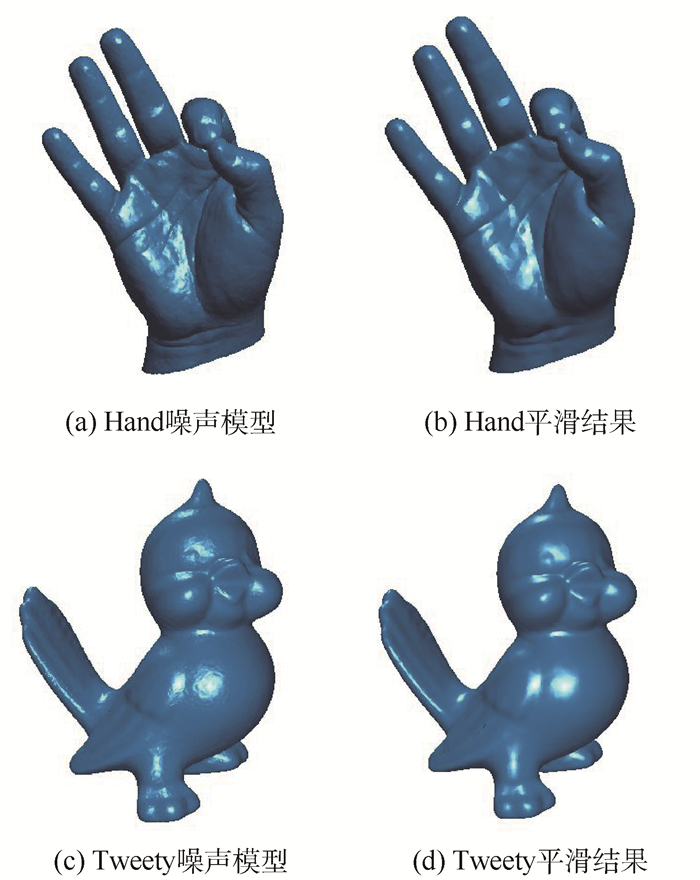
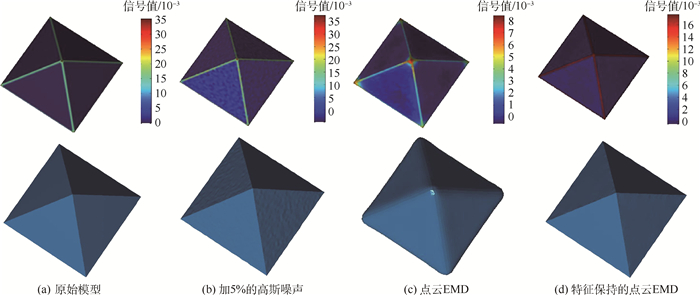
在计算机辅助设计与逆向工程应用中，针对缺乏拓扑连接关系的点云数据，提出了基于经验模态分解(EMD)的点云数据平滑与增强算法。首先，以点云模型的拉普拉斯矩阵坐标与法向的内积作为EMD输入信号，提取点云模型输入信号的极值点作为插值节点计算信号的上下包络；然后，为实现特征保持的EMD信号分解，通过检测点云数据上特征点，并在计算信号上下包络的过程中作为约束，克服传统EMD算法无法保持特征的局限；最后，迭代地从输入信号中减去上下包络的均值得到内蕴模态函数(IMF)和余量，并通过设计滤波器实现了点云数据平滑和增强。实验结果表明, 本文算法有效地将EMD推广到三维散乱点云数据中, 扩大EMD在三维几何中的应用范围，并在点云数据平滑和增强方面取得了很好的效果。
-
关键词:
- 经验模态分解(EMD) /
- 点云数据 /
- 数据平滑 /
- 数据增强 /
- 多尺度分解
Abstract:In applications of computer aided design and reverse engineering, for the data of point clouds without any topology information, we propose an effective smoothing and enhancing algorithm for point clouds based on empirical mode decomposition (EMD). First, the input signal of EMD is computed via the inner product of Laplacian vector and point's normal. For the input signal, the extreme points are extracted, and then the upper and lower envelopes are calculated by considering the extreme points as interpolating points. Second, in order to achieve feature preserving EMD signal decomposition, the sharp feature points are detected and considered as constrains in envelope computing. In this way, the over smoothing effect of traditional EMD algorithm can be effectively overcome. Finally, we can obtain the intrinsic mode function (IMF) and the residue by iteratively subtracting the mean of upper and lower envelops from the input signal in each iteration. Based on the multi-scale decomposition, different filter operators are designed to achieve point clouds smoothing and enhancing. Experimental results show that satisfactory smoothing and enhancing results of point clouds are obtained by the proposed novel EMD-based algorithm and EMD can be effectively extended to point clouds, which expands the application range of EMD in three-dimensional geometry processing.
-
图 3 Dragon点云模型的多尺度分解结果
Figure 3. Multi-scale decomposition results of Dragon point clouds model
图 4 Dodecahandle和Venubody模型的平滑结果
Figure 4. Smoothing results of Dodecahandle and Venubody models
图 8 Max Planck和Dog模型的平滑和增强结果
Figure 8. Smoothing and enhancing results of Max Planck and Dog models
表 1 各模型参数设置及运行时间统计
Table 1. Parameter setting and running time statistics for each model
模型 P NB nIMF 运行时间/s tL tEMD tTOTAL 八面体 4 098 15 3 3.835 5.425 9.670 Dragon 50 000 25 3 46.439 74.245 124.770 Dodecahandle 38 390 15 3 34.358 52.278 89.298 Venubody 11 362 15 3 10.502 15.229 26.529 Hand 20 002 15 3 18.076 27.015 46.500 Tweety 93 047 15 3 85.297 136.972 229.845 立方体 24 578 15 3 22.526 34.611 59.771 Fandisk 27 827 15 3 25.787 38.875 67.315 Max Planck 49 132 25 3 43.872 70.614 119.321 Dog 101 108 25 3 91.739 152.658 253.532 
下载: 导出CSV
-
[1] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society of London A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971):903-995. doi: 10.1098/rspa.1998.0193 [2] 郑有志, 覃征.基于二维经验模态分解的医学图像融合算法[J].软件学报, 2009, 20(5):1096-1105. http://www.cnki.com.cn/Article/CJFDTOTAL-RJXB200905005.htmZHENG Y Z, TAN Z.Medical images fusion algorithm based on dimensional empirical mode decomposition[J].Journal of Software, 2009, 20(5):1096-1105(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-RJXB200905005.htm [3] 徐琼, 李峰, 吕回.二维EMD分解的数字图像压缩[J].计算机工程与应用, 2009, 45(5):180-182. http://cdmd.cnki.com.cn/Article/CDMD-10536-2009168573.htmXU Q, LI F, LV H.Digital image compression of dimensional EMD decomposition [J].Computer Engineering and Applications, 2009, 45(5):180-182(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10536-2009168573.htm [4] 郭耸, 顾国昌, 李常有, 等.利用EMD的自适应图像去噪[J].计算机工程与应用, 2013, 49(8):12-16. http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201308006.htmGUO S, GU G C, LI C Y, et al.Adaptive image denoising based on EMD[J].Computer Engineering and Applications, 2013, 49(8):12-16(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201308006.htm [5] QIN X, CHEN X, ZHANG S, et al.EMD based fairing algorithm for mesh surface[C]//11th IEEE International Conference on Computer-Aided Design and Computer Graphics, 2009.Piscataway, NJ:IEEE Press, 2009:606-609. [6] WANG H, SU Z, CAO J, et al.Empirical mode decomposition on surfaces[J].Graphical Models, 2012, 74(4):173-183. doi: 10.1016/j.gmod.2012.04.005 [7] HU J P, WANG X C, QIN H.Improved, feature-centric EMD for 3D surface modeling and processing[J].Graphical Models, 2014, 76(5):340-354. doi: 10.1016/j.gmod.2014.03.006 [8] WANG X C, HU J P, ZHANG D B, et al.Efficient EMD and Hilbert spectra computation for 3D geometry processing and analysis via space-filling curve[J].The Visual Computer, 2015, 31(6):1135-1145. doi: 10.1007/s00371-015-1100-4 [9] SUBER K, SOLER C, DURAND F.Edge-preserving multiscale image decomposition based on local extrema[J].ACM Transactions on Graphics, 2009, 28(5):1-9. http://dl.acm.org/citation.cfm?id=1618493 [10] LUO C, ISSAM S, WANG Y.Approximating gradients for meshes and point clouds via diffusion metric[J].Computer Graphics Forum, 2009, 28(5):1497-1508. doi: 10.1111/cgf.2009.28.issue-5 [11] BELKIN M, SUN J, WANG Y.Constructing Laplace operator from point clouds in Rd[C]//ACM-SIAM Symposium on Discrete Algorithms.New York:SIAM, 2009:1031-1040. [12] LUO C, SUN J, WANG Y.Integral estimation from point cloud in d-dimensional space:A geometric view[C]//Proceedings of the 25th Annual Symposium on Computational Geometry.New York:ACM, 2009:116-124. [13] LIU J, CAO J, LIU X, et al.Mendable consistent orientation of point clouds [J].Computer-Aided Design, 2014, 55(3):26-36. http://www.sciencedirect.com/science/article/pii/S0010448514001006 [14] 王小超, 刘秀平, 李宝军, 等.基于局部重建的点云特征点提取[J].计算机辅助设计与图形学学报, 2013, 25(5):659-665. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198858.htmWANG X C, LIU X P, LI B J, et al.Feature point extraction from point clouds based local reconstruction [J].Journal of Computer-Aided Design & Computer Graphics, 2013, 25(5):659-665(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-1013198858.htm [15] FLEISHMAN S, DRORI I, COHEN-OR D.Bilateral mesh denoising [J].ACM Transactions on Graphics, 2003, 22(3):950-953. doi: 10.1145/882262 [16] LEVIN A, LISCHINSKI D, WEISS Y.Colorization using optimization [J].ACM Transactions on Graphics, 2004, 23(3):689-694. doi: 10.1145/1015706 [17] FLOATER M, HORMANN K.Parameterization of triangulations and unorganized points [M]//ISKE A, QUAK E, FLOATER M S.Tutorials on multiresolution in geometric modelling.Berlin:Springer, 2002:287-316. [18] HUANG H, LI D, ZHANG H, et al.Consolidation of unorganized point clouds for surface reconstruction [J].ACM Transactions on Graphics, 2009, 28(5):89-97. http://dl.acm.org/citation.cfm?doid=1661412.1618522 [19] HUANG H, WU S, GONG M, et al.Edge-aware point set resampling[J].ACM Transactions on Graphics, 2013, 32(1):60-61. http://web.siat.ac.cn/~vcc/publications/2012/edgeaware/ [20] GUENNEBAUD G, GROSS M.Algebraic point set surfaces[J].ACM Transactions on Graphics, 2007, 26(3):1-9. doi: 10.1145/1276377 -
下载:
点击查看大图
计量
- 文章访问数: 818
- HTML全文浏览量: 165
- PDF下载量: 475
- 被引次数: 0
