卫星天线复合材料框架的铺层优化设计

陶扬; 王春洁; 付志方

doi:10.13700/j.bh.1001-5965.2016.0392

卫星天线复合材料框架的铺层优化设计

doi: 10.13700/j.bh.1001-5965.2016.0392

陶扬¹,
王春洁^{1, 2, ,},
付志方¹

1.
北京航空航天大学机械工程及自动化学院, 北京 100083
2.
北京航空航天大学虚拟现实技术与系统国家重点实验室, 北京 100083

详细信息

作者简介:
陶扬，男，硕士研究生。主要研究方向：数字化设计及仿真

王春洁，女，博士，教授，博士生导师。主要研究方向：数字化设计及仿真

付志方，男，博士研究生。主要研究方向：机械设计、拓扑优化

通讯作者:
王春洁, E-mail: wangcj@buaa.edu.cn

中图分类号: V414.8
计量
- 文章访问数: 786
- HTML全文浏览量: 64
- PDF下载量: 433
- 被引次数: 0
出版历程
- 收稿日期: 2016-05-11
- 录用日期: 2016-08-10
- 网络出版日期: 2017-05-20

Layup design optimization of composite frame for satellite antenna

TAO Yang¹,
WANG Chunjie^{1, 2
, ,},
FU Zhifang¹

1.
School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
2.
State Key Laboratory of Virtual Reality Technology and System, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

More Information

Corresponding author: WANG Chunjie, E-mail:wangcj@buaa.edu.cn

摘要

摘要:
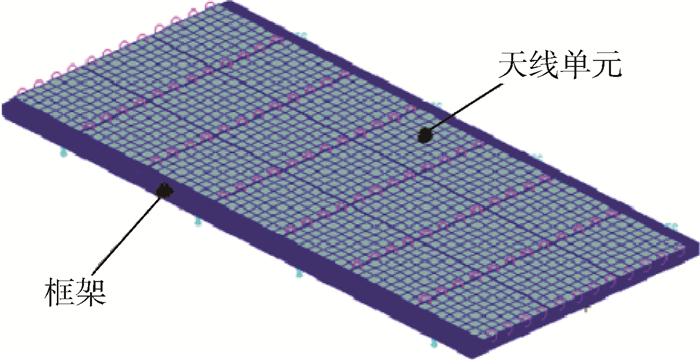
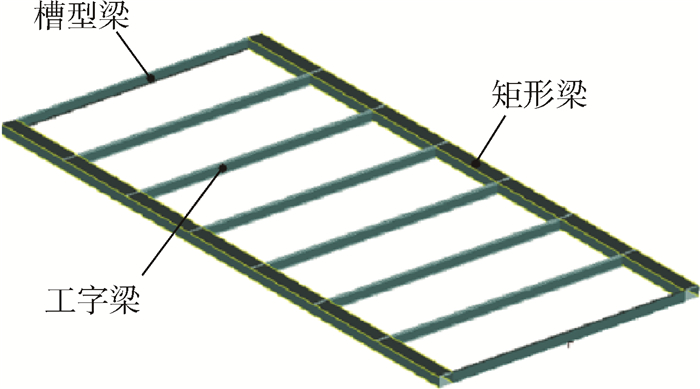
为了改善卫星天线复合材料框架的结构动力学性能，提出了一种针对卫星天线框架复合材料铺层的两阶段优化设计方法。阶段Ⅰ以各铺层的角度为设计变量进行铺层顺序优化，框架基频的最大化为优化目标，铺层数的最大值为约束条件。其中设计变量用一种多进制码来表示，并将多进制码映射为连续变量，应用粒子群优化(PSO)算法对阶段Ⅰ优化模型进行求解。在阶段Ⅰ优化结果的基础上，阶段Ⅱ主要是优化复合材料的层数，以基频最大化与质量最小化为优化目标建立多目标拓扑优化模型，应用第2代非劣排序遗传算法(NSGA-Ⅱ)进行求解。为了验证该方法的有效性，对某大型卫星天线复合材料框架进行优化设计，结果表明：该方法能有效地减小天线板复合材料框架的质量，并提高基频。
- 复合材料框架 /
- 卫星天线 /
- 两阶段优化 /
- 结构动力学性能 /
- 映射
Abstract:
A two-phase optimization method for layup design of composite frame for satellite antenna is introduced to improve the structural dynamics performance of the composite frame. Phase Ⅰ focused on generating a new ply layout by optimizing the ply orientation angle and stacking sequences, while the number of plies is the upper bound of the constraints. The objective of the first phase was to maximize the fundamental frequency of the frame. Design variables were n-nary codes which were mapped to continuous variables. The optimization model of phase Ⅰ was solved by the particle swarm optimization (PSO) algorithm. Phase Ⅱ aimed to reduce the number of plies for the ply layout optimized in phase Ⅰ. A multi-objective topology optimization model was built to minimize the mass of the frame and maximize the fundamental frequency. The optimization model was solved by the non-dominated sorting genetic algorithm Ⅱ (NSGA-Ⅱ). To verify the feasibility of optimization method, the example of a frame of large satellite antenna was conducted. The result shows that the two-phase optimization can effectively reduce the mass of the frame of large satellite antenna and also improve the fundamental frequency.
- composite frame /
- satellite antenna /
- two-phase optimization /
- structural dynamics performance /
- mapping

HTML全文

图 1 卫星天线复合材料框架铺层设计优化流程图

Figure 1. Flowchart of layup design optimization of composite frame for satellite antenna

下载: 全尺寸图片幻灯片

图 2 卫星天线装配图

Figure 2. Assembly drawing of satellite antenna

下载: 全尺寸图片幻灯片

图 3 卫星天线框架

Figure 3. Frame of satellite antenna

下载: 全尺寸图片幻灯片

图 4 框架的8个约束点位置

Figure 4. Position of eight constraint points of frame

下载: 全尺寸图片幻灯片

图 5 矩形梁、工字梁及槽型梁

Figure 5. Rectangular beam, I-shape beam and U-shape beam

下载: 全尺寸图片幻灯片

图 6 Pareto前沿对比

Figure 6. Comparison of Pareto frontiers

下载: 全尺寸图片幻灯片

图 7 不同初始层数下的Pareto前沿对比

Figure 7. Comparison of Pareto frontiers for different initial layups

下载: 全尺寸图片幻灯片

表 1 PSO参数设置

Table 1. Parameters setting of PSO

参数	最大迭代次数	粒子数	惯性权重	全局增量	粒子增量	最大搜索速度
数值	20	12	0.9	0.9	0.9	0.1

下载: 导出CSV

表 2 阶段Ⅰ求解结果

Table 2. Solving results of phase Ⅰ

变量类型	x₁(铺层序列)	x₂(铺层序列)	x₃(铺层序列)	基频/Hz	质量/kg	迭代次数
连续变量	[33122210101021033203]	[21111311111131111111]	[11112212012202301102]	53.93	45.71	20
离散变量	[21031003122122102102]	[13131113131112111110]	[13101011220213222221]	52.49	45.71	20

下载: 导出CSV

表 3 NSGA-Ⅱ参数设置

Table 3. Parameters setting of NSGA-Ⅱ

参数	种群大小	迭代次数	交叉概率	交叉分布指数	变异分布指数
数值	12	30	0.9	10	20

下载: 导出CSV

表 4 阶段Ⅱ的Pareto最优解集

Table 4. Pareto optimal solution set of phase Ⅱ

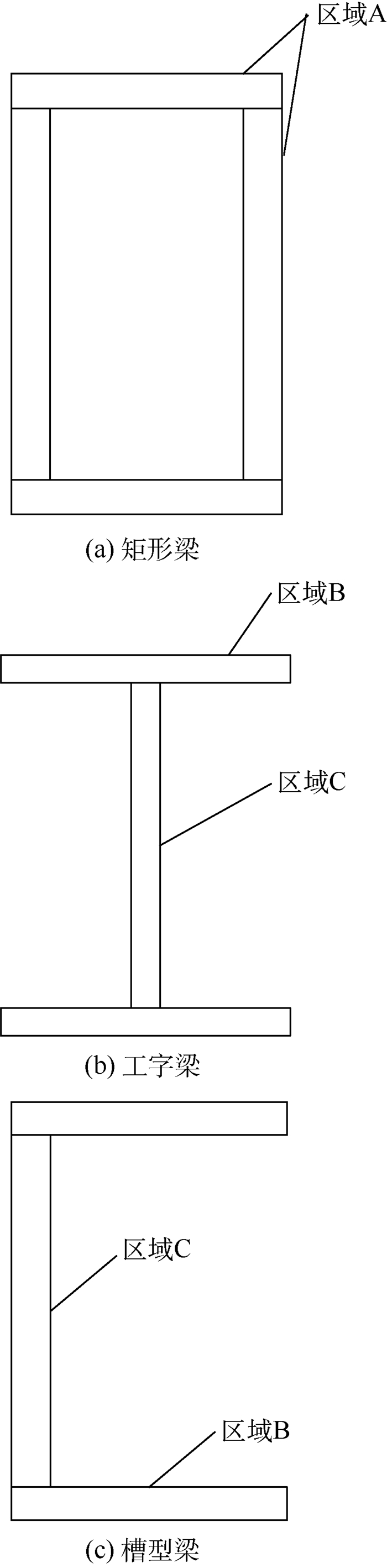
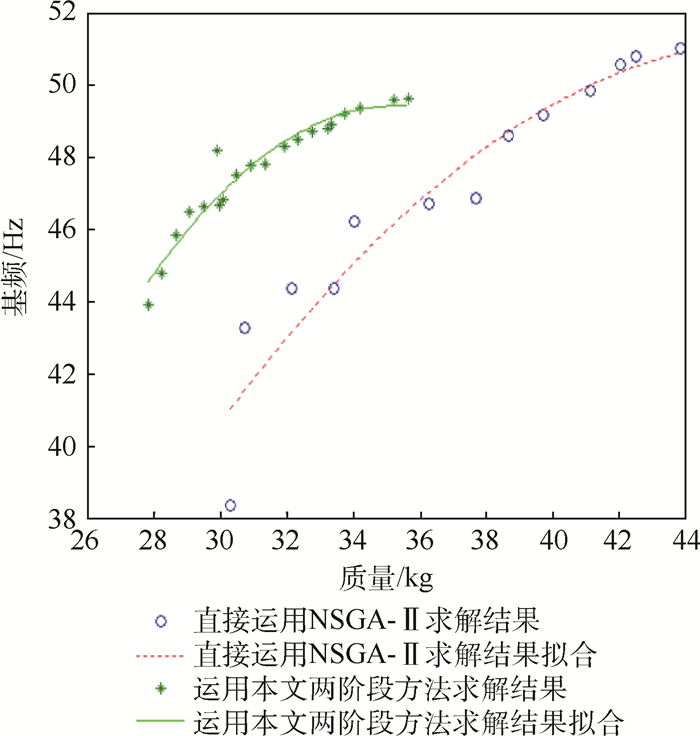
方案	区域A(铺层序列)	区域B(铺层序列)	区域C(铺层序列)	基频/Hz	质量/kg
原始方案	[1023102310231023]	[1023102310231023]	[1023102310231023]	41.421	38.37
1	[332210012032]	[1113111111111111]	[11221212030102]	46.657	29.97
2	[33221001020320]	[21113111111111111]	[112121203102]	48.460	32.32
3	[332201020323]	[11131111111111]	[112122031102]	44.791	28.24
4	[332210002032]	[1113111111111111]	[112121200102]	46.479	29.06
5	[332210002032]	[111311111111111]	[112121200102]	45.816	28.65
6	[3322100102032]	[111311111111111]	[112121200102]	46.807	30.08
7	[332210101020320]	[21113111111111111]	[112121203102]	49.171	33.75
8	[3322101010203203]	[1113111111111111]	[1121212031102]	49.549	35.21
9	[33221001020320]	[1113111111111111]	[112121200102]	48.277	31.91
10	[33220101021020]	[111131111111111111]	[112212010011]	48.169	29.89
11	[3322100102032]	[1113111111111111]	[112121200102]	47.481	30.49
12	[33221001020320]	[21113111111111111]	[11212120301102]	48.761	33.22
13	[3322100102032]	[21113111111111111]	[112121200102]	47.748	30.90
14	[332210002032]	[21113111111111111]	[112212120102]	46.630	29.48
15	[332210101020320]	[1113111111111111]	[121220301102]	48.887	33.33
16	[3322100102032]	[21113111111111111]	[1121212030102]	47.799	31.35
17	[33221001020320]	[21113111111111111]	[1121212001102]	48.712	32.77
18	[332210101020320]	[21113111111111111]	[1121212030102]	49.326	34.20
19	[3322101010203203]	[1113111111111111]	[11212120231102]	49.613	35.66
20	[332201020323]	[1113111111111]	[112220231102]	43.912	27.83

下载: 导出CSV

参考文献(16)

[1]	孙士平, 张卫红.基于改进模拟退火算法的复合材料层合板频率优化[J].复合材料学报, 2015, 32(3):902-910. http://www.cnki.com.cn/Article/CJFDTOTAL-FUHE201503037.htm SUN S P, ZHANG W H.Frequency optimization of composite laminates using an improved simulated annealing algorithm[J].Acta Materiae Compositae Sinica, 2015, 32(3):902-910(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-FUHE201503037.htm
[2]	晏飞, 李为吉.基于改进遗传算法的复合材料层合板自振频率优化设计[J].机械科学与技术, 2000, 19(增刊):91-96. http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX2000S1038.htm YAN F, LI W J.Optimal design of composite laminates subject to natural frequency constraint using an improved genetic algorithm[J].Mechanical Science and Technology, 2000, 19(Suppl.):91-96(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JXKX2000S1038.htm
[3]	柯俊, 史文库, 钱琛, 等.采用遗传算法的复合材料板簧多目标优化方法[J].西安交通大学学报, 2015, 49(8):102-108. doi: 10.7652/xjtuxb201508017 KE J, SHI W K, QIAN C, et al.A multiobjective optimization for composite leaf springs using genetic algorithm[J].Journal of Xi'an Jiaotong University, 2015, 49(8):102-108(in Chinese). doi: 10.7652/xjtuxb201508017
[4]	HONDA S, NARITA Y, SASAKI K.Discrete optimization for vibration design of composite plates by using lamination parameters[J].Advanced Composite Materials, 2009, 18(4):297-314. doi: 10.1163/156855109X434739
[5]	NARITA Y.Layerwise optimization for the maxi-mum fundamental frequency of laminated composite plates[J].Journal of Sound and Vibration, 2003, 263(5):1005-1016. doi: 10.1016/S0022-460X(03)00270-0
[6]	GHIASI H, FAYAZBAKHSH K, PASINI D, et al.Optimum stacking sequence design of composite materials Part Ⅱ:Variable stiffness design[J].Composite Structures, 2010, 93(1):1-13. doi: 10.1016/j.compstruct.2010.06.001
[7]	ABDALLA M M, SETOODEH S, GURDAL Z.Design of variable stiffness composite panels for maxi-mum fundamental frequency using lamination parameters[J].Composite Structures, 2007, 81(2):283-291. doi: 10.1016/j.compstruct.2006.08.018
[8]	STEGMAN J, LUND E.Discrete material optimization of general composite shell structures[J].International Journal for Numerical Methods in Engineering, 2005, 62(14):2009-2027. doi: 10.1002/(ISSN)1097-0207
[9]	冯消冰, 黄海, 王伟.基于遗传算法的大型风机复合材料叶片根部强度优化设计[J].复合材料学报, 2012, 29(5):196-202. http://www.cnki.com.cn/Article/CJFDTOTAL-FUHE201205033.htm FENG X B, HUANG H, WANG W.Strength optimization of large wind turbine blade root on the genetic algorithm[J].Acta Materiae Compositae Sinica, 2012, 29(5):196-202(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-FUHE201205033.htm
[10]	穆朋刚, 赵美英, 陈鹏飞, 等.基于蚁群算法的复合材料层合板的铺层顺序优化[J].玻璃钢/复合材料, 2007, 11(6):14-17. http://www.cnki.com.cn/Article/CJFDTOTAL-BLGF200706003.htm MU P G, ZHAO M Y, CHEN P F, et al.Ply stacking-sequence optimization of composite laminate plates by ant colony system[J].Fiber Reinforced Plastics/Composites, 2007, 11(6):14-17(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-BLGF200706003.htm
[11]	顾元宪, 亢战, 赵国忠, 等.卫星承力筒复合材料结构的优化设计[J].宇航学报, 2003, 24(1):88-91. http://www.cnki.com.cn/Article/CJFDTOTAL-YHXB200301016.htm GU Y X, KANG Z, ZHAO G Z, et al.Optimal design of composite structure of satellite bearing cylinder[J].Journal of Astronautics, 2003, 24(1):88-91(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-YHXB200301016.htm
[12]	陈烈民, 杨宝宁.复合材料的力学分析[M].北京:中国科学技术出版社, 2006:98-101. CHEN L M, YANG B N.Mechanical analysis for composite materials[M].Beijing:Science and Technology of China Press, 2006:98-101(in Chinese).
[13]	陈烈民.航天器结构与机构[M].北京:中国科学技术出版社, 2005:102-103. CHEN L M.Spacecraft structures and mechanisms[M].Beijing:Science and Technology of China Press, 2005:102-103(in Chinese).
[14]	唐俊.PSO算法原理及应用[J].计算机技术与发展, 2010, 20(2):213-216. http://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ201002057.htm TANG J.Principle and application of PSO algorithm[J].Computer Technology and Development, 2010, 20(2):213-216(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-WJFZ201002057.htm
[15]	MARLE R T, ARORA J S.Survey of multi-objective optimization methods for engineering[J].Structural and Multidisciplinary Optimization, 2004, 26(6):369-395. doi: 10.1007/s00158-003-0368-6
[16]	DEB K, PRATAP A, AGARWAL S, et al.A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2):182-197. doi: 10.1109/4235.996017