-
摘要:
针对现有交替数字二叉树(ADT)方法的不足,引入辅助笛卡儿网格提出了一种基于散列数据结构的改进搜索方法以缓解可能出现堆栈溢出的问题和提高重叠网格装配的效率。该方法以散列数据结构的方式对网格单元进行存储和搜索,首先以辅助笛卡儿网格对网格单元的存储空间进行初步映像,然后基于ADT搜索树作进一步检索。在ADT搜索方法的基础上,笛卡儿网格的引入进一步缩小了网格单元的搜索范围使得改进方法具有更好的效率。基于单个网格节点,查询深度和搜索耗时的测试显示改进方法相比现有ADT搜索方法能使挖洞的平均效率提高25%以上。此外,挖洞结果和基于网格装配的数值计算验证了改进搜索方法在重叠网格装配中的可靠性。
-
关键词:
- 重叠网格 /
- 网格装配 /
- 交替数字二叉树(ADT) /
- 贡献单元 /
- 搜索方法
Abstract:An improved searching method of alternating digital tree (ADT) is proposed for making up the deficiency of the existing ADT method and improving the efficiency of the overlapping grid assembly. The new method stores and retrieves donor cells based on a hash data structure, in which an auxiliary Cartesian mesh is first applied to map the storage address similar to the table of contents in hash table, and then a node-oriented ADT is used for further retrieval in accordance with the aforementioned storage space. Based on ADT search, the introduction of the Cartesian mesh can further narrow the search scope of donor cell, which makes the present one have better efficiency. Tests of searching depth and time consumption based on several discrete grid nodes indicate that the present method can enhance the average hole-cutting efficiency by more than 25% compared with the existing ADT method. Moreover, the hole-cutting results and numerical computations of typical configurations confirm the reliability of the improved ADT searching method in overlapping grid assembly.
-
Key words:
- overlapping grid /
- grid assembly /
- alternating digital tree (ADT) /
- donor cell /
- searching method
-
重叠网格是模拟刚体运动绕流的一种重要网格方法[1]。重叠网格的前处理过程称为网格装配,这个过程决定怎样挖洞以及插值区域如何选择。因此,网格装配过程可以分为挖洞和建立插值边界2个主要步骤[2-3]。然而,挖洞过程和建立插值边界都需要频繁地进行贡献单元检索,使得寻找网格节点的贡献单元成为网格装配过程的主要负担。于是,选择快速、高效的贡献单元搜索方法对提高网格装配效率至关重要。目前,比较常用的贡献单元搜索方法有反变换法[4-5]、相邻格点搜索法[6-7]以及基于高效查询数据结构的空间搜索算法[8-9]。
反变换法[4-5]通常采用三线性插值方法[10]获得曲线坐标系网格与均匀笛卡儿网格的变换关系,并通过相应的变换关系能迅速计算物理空间点在均匀笛卡儿空间中的位置。由于曲线坐标系网格与均匀笛卡儿网格的一一对应关系,从而也就确定了贡献单元在物理网格中的相对位置。反变换法不适用于非结构网格或混合网格, 主要用于结构网格。该方法定位迅速,搜索效率较高。它的主要问题在于变换过程需要求解一组线性方程,迭代过程影响了计算效率。
相邻格点搜索法[6-7]是一种模版跳跃法[11],它以物理空间点到候选包围单元中心的距离为判断依据,通过比较寻找最近单元,并在最近单元的附近区域查询真实贡献单元。相邻格点搜索法是一种仅次于反变换法的快速搜索方法,在非结构网格中应用较广,虽然对结构网格也适用,但由于搜索过程会在对接边界处中断,有时会影响单元搜索的准确性。因此,在结构网格中应用该方法须要解决跨区域搜索带来的问题。此外,该方法对起始单元依赖较大,起始单元选取的好坏严重影响它的可靠性和高效性,如何确定合适的起始单元是使用此类方法的最大困难。
基于高效查询数据结构的空间搜索算法是依靠高效的数据存储方式来加快搜索的一类方法。这种方法也对应着一种空间分解算法,例如交替数字二叉树(Alternating Digital Tree, ADT)[8, 12]、K-D树(K-Dimensional tree)[9, 13]等。其中,基于ADT的搜索方法[12]最有代表性[14]。在该方法中,每个ADT节点对应着一个笛卡儿空间,当其作为子树根节点时,它的笛卡儿空间包含所有子节点的笛卡儿空间;而作为子节点时,它的笛卡儿空间被其父节点对应的笛卡儿空间所包含。ADT搜索方法利用以上层次包含关系,结合笛卡儿包围盒相交判断关系的简单原理,忽略对不与目标空间相交的所有子空间的查询。于是,只要子树根节点所对应的子空间不与目标空间相交,则子树中所有子节点均将在查询中被忽略,从而大大减少了查询次数,提高了搜索效率。同时,该算法特别适合于存储几何不规则的空间单元。然而,该方法需要占用额外存储空间,在进行大规模数值模拟时,大网格量所带来的搜索深度增加也会影响搜索的效率,甚至可能出现“堆栈溢出”问题,导致搜索失败。
在上述搜索方法中,ADT作为一种特殊的二叉搜索树具有很高的搜索效率,且非常适合存储离散和不规则的几何元素。因此,本文在结构重叠网格的装配过程中使用ADT存储和搜索贡献单元,并引入辅助笛卡儿网格提出了一种基于散列数据结构的改进方法以改善ADT数据结构的缺点和提高挖洞过程的整体效率。在算例验证中,首先从30P30N翼型和直机翼-带舵导弹模型的网格中分别选取3组典型的离散网格点开展贡献单元查询深度测试以考查改进搜索方法的效率。同时,通过挖洞过程的计算耗时对比进一步验证改进搜索方法相比于现有ADT搜索的效率提高能力。其次,通过网格装配结果考核改进搜索方法和挖洞方法的有效性。最后,应用自主开发的可压缩气动力/热/燃烧数值模拟程序(Aerodynamics Combustion Aerothermo-dynamics Numerical Simulation, ACANS)[15-16]对基于重叠网格装配结果的算例[17-18]进行数值模拟和可靠性验证。
1. 重叠网格装配方法
本文结合洞映射法[19]和割补法[20-21]实现挖洞过程。首先,以壁面边界作为初始挖洞阵面,使用基于洞映射与查询包围单元的组合方式判断网格节点在洞内外的情形,实现初步挖洞。之后,在初步挖洞形成边缘节点的基础上,通过割补法实现阵面推进和缩小重叠区域。借鉴隐式挖洞[22]的处理方法,本文在现有割补法的基础上引用网格单元体积作为判据控制阵面的推进距离,以满足插值区网格单元大小不会相差过于悬殊的要求。
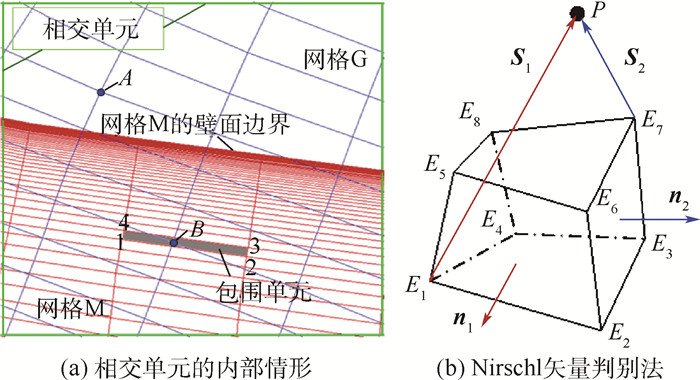
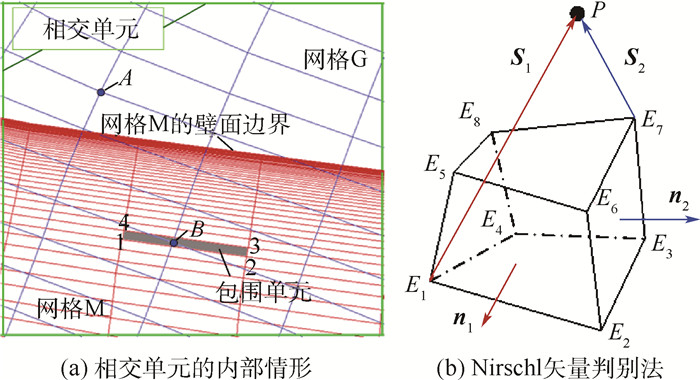
包围单元法主要应用于洞映射过程以判别落入相交单元的网格节点在洞内外的情况。其基本原理如图 1(a)所示,如果网格G与网格M有重叠,若G中的网格节点P位于M的计算域内,则在网格M中一定能找到一个网格单元包含节点P。相反,若找不到这样的包围单元,则P一定在M所表示的计算域之外。查询包围单元的具体过程如下:首先,对网格节点进行区分,即标记网格节点所属的块编号以及网格块所属的超块[23]编号。其次,在相交单元中寻找距离待查网格节点最近的壁面网格单元。如果最近壁面网格单元与当前待查网格节点属于同一超块,则网格节点必为计算点。否则,在壁面网格单元所属的超块中,寻找待查网格节点的贡献单元。若找到贡献单元,则待查网格节点为计算点,否则为无效点。
查询包围单元也是一个搜索贡献单元的过程(搜索方法详见第2节)。在搜索贡献单元的过程中,须要逐一判断网格点与某些网格单元的空间关系。为此,本文采用Nirschl矢量判别法[24]判断空间点在几何单元体的内外情形,如图 1(b)所示,图中:n1和n2分别对应面的外法向量;S1和S2则是由顶点到指定节点的方向向量。
2. 贡献单元搜索方法
贡献单元搜索过程是从大量甚至海量的网格单元中定位可能的某个或几个网格单元,并从中找到正确的网格单元作为贡献单元的过程。本文基于散列数据结构建立了一种改进ADT搜索方法用于网格装配过程的贡献单元搜索。以下分别从散列表搜索方法、基于网格节点的ADT法以及改进ADT搜索方法等方面做详细介绍。
2.1 散列表搜索方法
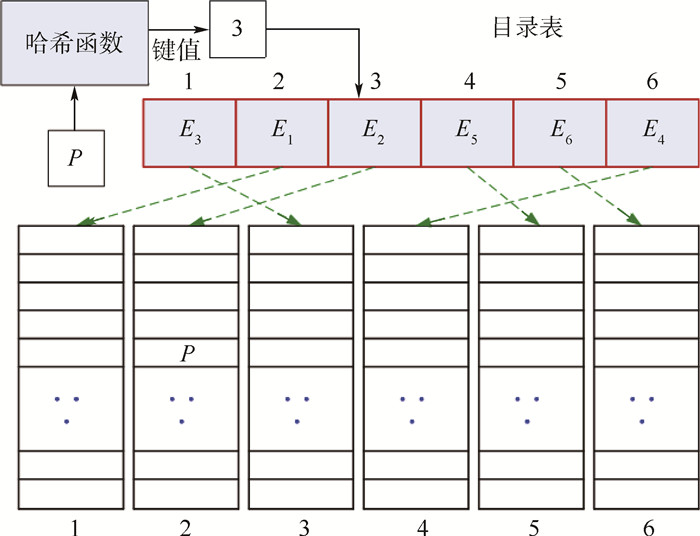
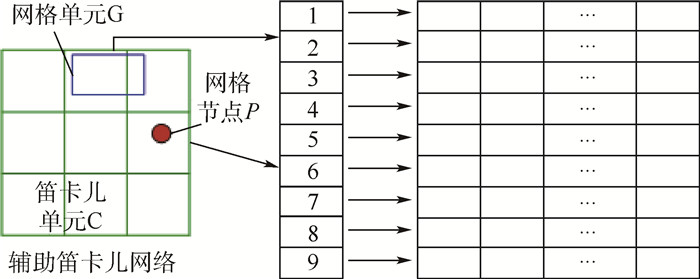
散列表是一种分布式存储数据结构。如图 2所示,散列结构利用一张目录表对元素存储地址进行映射和分配。当存取元素P时,首先通过特定的哈希函数进行散列,获得元素P在目录表中的地址(或键值),然后通过该地址从目录表中获得元素P所在存储空间的起始位置,最后通过遍历数组空间获得元素P的具体存储位置。
本文提出的散列表法实际上是一种基于辅助笛卡儿网格的贡献单元搜索方法。该方法利用笛卡儿网格作为目录表对几何元素进行存储映像和分配。如图 3所示,如果给定的几何元素与某笛卡儿单元相交,就将该几何元素存入笛卡儿单元对应的存储数组中。同理,查询几何元素时,首先判断该几何元素所在的笛卡儿单元,然后转到该笛卡儿单元所关联的数组空间中寻找该几何元素。
在上述存储或查询的过程中,计算几何元素所在笛卡儿单元的方法类似为一个哈希函数,即

(1) 式中:(ξ, η, ζ)为笛卡儿单元在辅助笛卡儿网格中的位置坐标; ni和nj分别为笛卡儿网格在i和j方向的单元个数。笛卡儿网格的单元个数由外部设置的无量纲参数l(0 < l < 1) 来控制。设笛卡儿空间的左下角点和右上角点分别为P1(xmin, ymin, zmin)和P2(xmax, ymax, zmax),则各方向的单元个数分别为

(2) 式中:L=l·Lmax为笛卡儿单元的实际边长,Lmax=max{xmax-xmin, ymax-ymin, zmax-zmin}。
若几何元素是一个空间节点P(x, y, z),则它所在的笛卡儿单元为

(3) 而对于网格单元,则以它的一个节点代表整个单元。例如在二维结构网格中,以N(i, j, k)代表由N(i, j, k)、N(i+1, j, k)、N(i+1, j+1, k)和N(i, j+1, k)4个顶点构成的网格单元,三维同理。其中(i, j, k)表示网格点在结构网格中的位置坐标。
由上述原理可知,散列表搜索方法是通过均匀分割笛卡儿空间来减小查询范围和减少搜索网格单元个数的搜索方法。由空间几何学可知,与笛卡儿单元相交的网格单元都有可能是落入相同单元中某个空间点的贡献单元。在网格处理时,如果笛卡儿网格单元越小,那么与之相交的网格单元个数也就可能越少。如果笛卡儿网格单元个数足够多,将会很大地减少搜索网格单元的次数,从而提高搜索效率。此外,如果笛卡儿网格单元所对应的存储空间采用数组结构,则低效的遍历检索将影响散列表搜索方法效率的进一步提高。因此,改变笛卡儿网格单元所对应的存储结构,使用比数组更加高效的数据结构可以帮助提高这种搜索方法的效率。
2.2 基于网格节点的ADT搜索方法
ADT[8]是一种二叉树搜索数据结构,特别适合无序离散空间点的存储和检索。针对网格单元的存储和搜索,本文设计了一种存储网格节点的ADT,其主要实现过程描述如下:
1) 建立覆盖重叠区域的辅助笛卡儿网格,并计算原始网格的最大单元边长e。
2) 以网格节点在结构网格中的位置坐标表示网格单元(类似2.1节所述方法)。ADT的每个节点除存储笛卡儿单元的空间信息、父节点和2个子节点的指针外,还将存储网格的序号m和单元在结构网格中的位置坐标(i, j, k)。
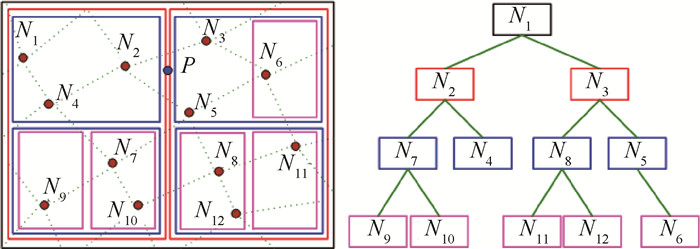
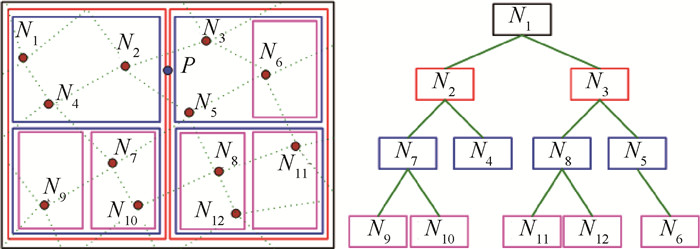
3) 遍历网格,根据网格存储顺序依次加入网格节点建立ADT。其具体建立方法参考文献[8],图 4给出了基于网格节点建立ADT的一个简单例子。
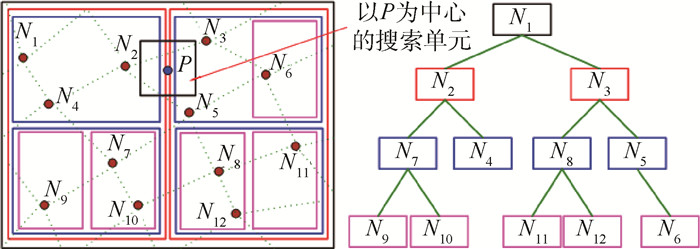
4) 以空间节点P(x, y, z)为例搜索贡献单元,首先以点P为中心、r=e/2+0.1为半边长构造包含点P的搜索单元(见图 5)。之后从根节点开始,依据搜索单元与ADT节点对应的笛卡儿空间是否相交为线索,查询ADT子树,获取贡献单元。
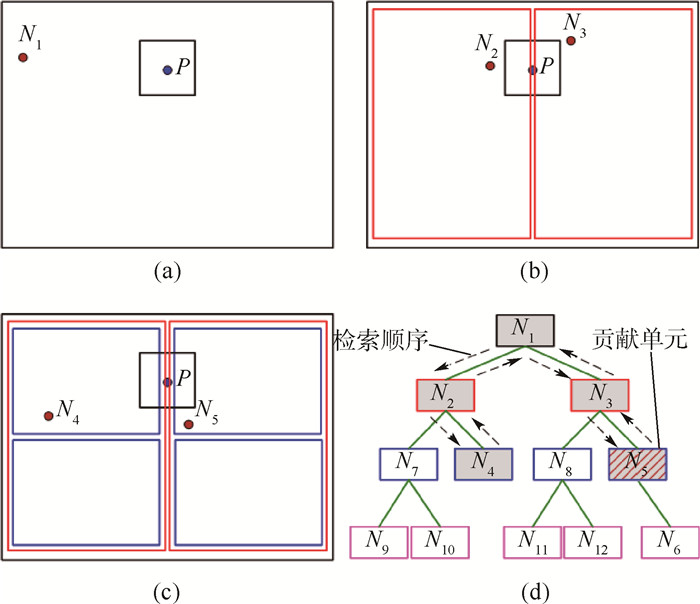
ADT子树查询是一个递归过程,取子树根节点,递归运算的具体处理方法为:① 如果当前ADT节点所存储的网格单元是所寻的贡献单元,或者当前ADT节点的左子节点和右子节点都不存在,则结束检索。② 取出一个子节点,判断子节点所表示的笛卡儿空间是否与搜索单元相交,如果相交,则以该子节点作为根节点查询它的子树空间;否则,忽略该子树的所有网格单元。
再以图 4为例,点P的贡献单元位于存储网格节点N5的ADT节点中。从根节点开始,由于点P的搜索单元分别与存储网格节点N1、N2、N3、N4和N5的ADT节点所对应的笛卡儿空间相交,于是通过查询顺序N1→N2→N4→N3→N5最终找到贡献单元,即以网格节点N5所表示的网格单元。这个查询过程如图 6所示。
当代表网格单元的网格节点被定位于ADT节点所对应的笛卡儿空间,则上述网格单元与笛卡儿空间一定相交。若搜索单元也与ADT节点对应的笛卡儿空间相交,基于网格节点的ADT搜索方法认为点P应位于ADT节点所存储的网格单元内。否则点P不可能在ADT节点所存放的网格单元内,更不可能在其子树节点所存储的网格单元内,因此无须在其子树中进行查寻。可见,基于网格节点的ADT搜索方法可以减少查询网格单元的次数,提高贡献单元的搜索效率。
在大规模网格处理过程中,单独的ADT搜索方法随着网格量增加,ADT节点增多,搜索深度增加,可能产生“堆栈溢出”等问题,导致程序崩溃和搜索失败。因此,减少ADT的节点个数,降低ADT的搜索深度是非常必要的。那么,引入多ADT数据结构是一种可行的解决办法。
2.3 基于散列数据结构的改进ADT搜索方法
由于散列搜索可起到初步缩小检索范围的作用,且映射过程简单高效。因此,本文在ADT搜索的基础上引入辅助笛卡儿网格,建立了基于散列数据结构的改进ADT搜索方法。首先建立辅助笛卡儿网格对网格区域进行分割,并以笛卡儿网格的有序存储空间作为散列目录表,然后以2.2节所述方法在每个笛卡儿单元中建立ADT以存储那些与该笛卡儿单元相交的网格单元。贡献单元检索时,首先通过辅助笛卡儿网格确定待查网格点的大体分布区域,然后在笛卡儿单元对应的ADT子树中进一步查询贡献单元。在这种混合搜索中,笛卡儿网格单元所对应的存储结构不再是数组形式,而是效率更高的ADT数据结构。因此,改进方法是基于散列表的多ADT数据结构(如图 7所示)。
对于改进搜索方法的效率预估,假设重叠网格的单元个数为n,则数组存储方式的网格单元平均搜索次数为(1+n)/2次,平均搜索耗时为O(n)。若采用二叉树存储,则网格单元的平均搜索次数约为(lb n)/2次,平均搜索耗时为O(lb n)。混合搜索首先利用辅助笛卡儿网格确定搜索区间,使得目标搜索区域内的网格单元个数可以减少为n/m(m为笛卡儿网格单元个数)。其次通过ADT存储和检索网格单元,由于每个ADT的最佳高度为lb(n/m),使得平均搜索次数变为(lb(n/m))/2次。可见,相比于单一ADT,混合搜索的平均搜索次数可以减少(lb m)/2次,平均搜索耗时可以减少O(lb m)。对于大规模数值计算,混合搜索数据结构有助于明显减少网格单元的搜索次数,提高ADT搜索的效率,同时对缓解“堆栈溢出”问题也有较大帮助。
上述搜索方法首先通过散列表减小搜索范围,然后利用ADT搜索进一步减少搜索次数。因此,这种组合方式是对单一ADT搜索方法的一种改进思想,可帮助提高贡献单元的搜索效率。
3. 效率测试和数值验证
3.1 贡献单元搜索效率
3.1.1 查询深度测试
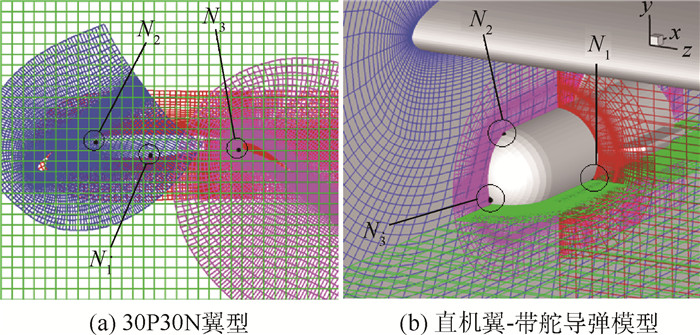
基于30P30N翼型和直机翼-带舵导弹(Wing/Finned-Store, WFS)模型的重叠网格,以下分别选取3组典型的离散网格点,应用所提出的改进ADT搜索方法以及现有ADT搜索方法进行贡献单元查询,通过查询深度和平均搜索耗时的对比考查改进方法的效率。
在30P30N翼型算例中,3组网格节点分别为:N1(0.430, -0.023)、N2(0.180, 0.038) 和N3(0.834, 0.003),而直机翼-带舵导弹模型的3组网格节点分别选取N1(2.952, -2.266, 0.401)、N2(1.842, -1.553, 0) 和N3(1.549, -2.202, 0),测试点的位置如图 8所示。
ADT搜索使用Fortran90语言和基于指针与结构体的递归函数实现,搜索深度测试在台式计算机(Intel Pentium CPU G645) 上采用串行计算方式实现,控制笛卡儿单元个数的无量纲参数l=0.04,应用改进方法与现有ADT搜索方法的测试结果分别由表 1和表 2所示。
表 1 30P30N翼型的搜索深度测试结果Table 1. Test results of searching depth for 30P30N airfoil节点编号 搜索深度/次 搜索耗时/ms 搜索耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 N1 2 884 1 120 0.312 5 0.125 0 60.00 N2 8 492 4 630 0.937 5 0.625 0 33.33 N3 14 588 9 499 1.250 0 0.937 5 25.00 表 2 直机翼-带舵导弹模型的搜索深度测试结果Table 2. Test results of searching depth for WFS model节点编号 搜索深度/次 搜索耗时/ms 搜索耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 N1 23 818 19 516 8.125 6.562 5 19.23 N2 46 971 22 440 15.938 7.187 5 54.90 N3 89 508 67 443 30.313 22.813 0 24.74 以上针对单个网格点的测试结果显示,基于散列数据结构的改进ADT搜索方法在查询深度和平均耗时上均明显优于现有的ADT搜索方法。可见,改进方法可明显提高ADT搜索的查询效率。
3.1.2 搜索耗时统计
为了进一步验证改进ADT搜索方法在网格装配中的整体效率,再次应用上述模型对该方法在挖洞过程中的平均搜索耗时进行统计。在洞映射挖洞过程中,主要采用查询贡献单元的方式判断相交单元内网格节点在洞内外的情形。而在优化挖洞过程中,主要测试采用割补法进行挖洞的效率。
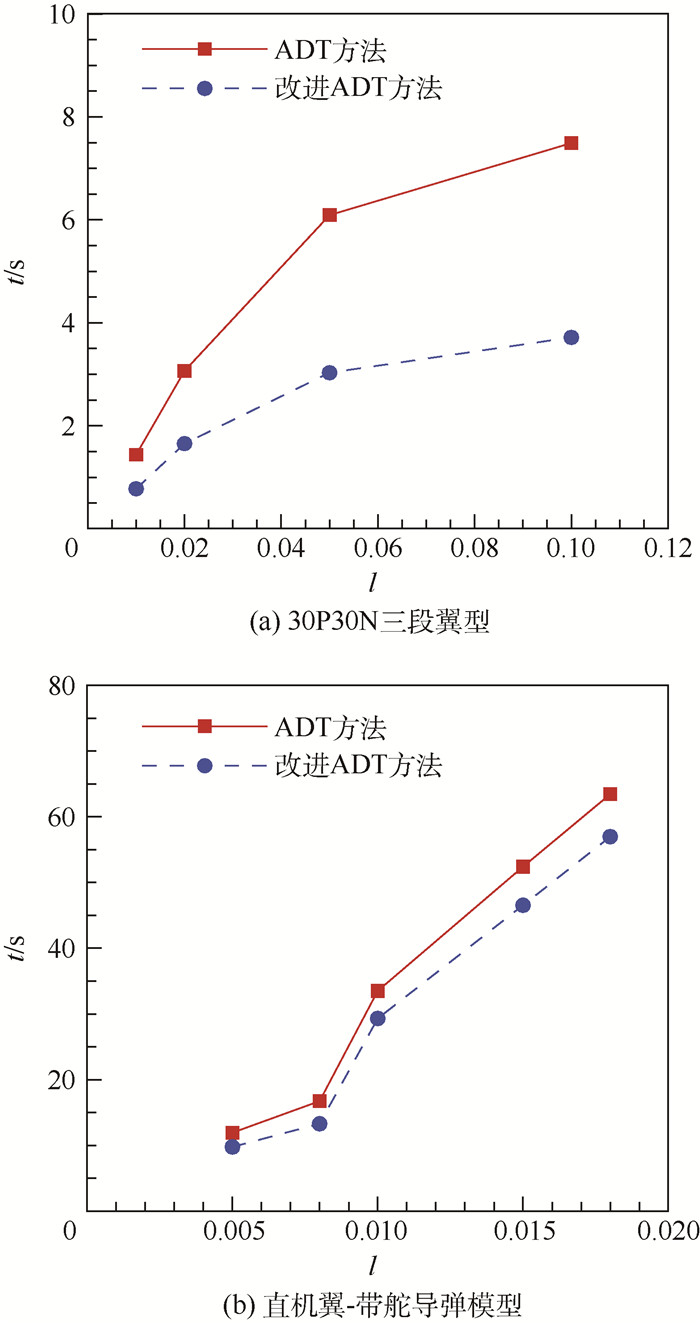
洞映射过程的统计耗时如图 9所示。其中无量纲参数l是确定笛卡儿网格单元个数的关键参数。优化挖洞过程和整个挖洞过程的统计耗时如表 3和表 4所示。由图 9、表 3和表 4的挖洞耗时统计显示,相比现有的ADT搜索方法,改进ADT方法在洞映射挖洞和割补法挖洞中均具有更小的计算耗时。对于整个挖洞过程,改进ADT方法在30P30N算例中的平均搜索耗时提高了40%以上,而在直机翼-带舵导弹模型中提高了25%以上。可见,改进ADT搜索方法在重叠网格装配中具有明显的效率改进。
表 3 30P30N三段翼型的挖洞耗时Table 3. Hole-cutting time consumption of three-element 30P30N airfoill 优化挖洞耗时/s 全部挖洞耗时/s 全部挖洞耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 0.01 30.640 6 18.066 4 32.156 3 18.851 6 41.38 0.02 30.625 0 18.105 5 33.871 1 19.785 2 41.59 0.05 30.714 8 18.179 7 37.152 3 21.238 3 42.83 0.10 30.898 4 18.128 9 38.796 9 21.914 1 43.52 表 4 直机翼-带舵导弹模型的挖洞耗时Table 4. Hole-cutting time consumption of WFS modell 优化挖洞耗时/s 全部挖洞耗时/s 全部挖洞耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 0.005 220.454 154.092 232.382 2 163.859 4 29.49 0.010 216.739 153.463 250.248 8 182.775 3 26.96 0.015 221.128 152.766 273.539 3 199.316 0 27.13 0.018 219.326 154.508 282.780 9 211.487 7 25.21 3.2 重叠网格挖洞效果
再次选取上述二维30P30N三段翼型与三维直机翼-带舵导弹模型的网格装配作为典型算例对基于改进ADT搜索方法的挖洞过程的有效性进行验证。
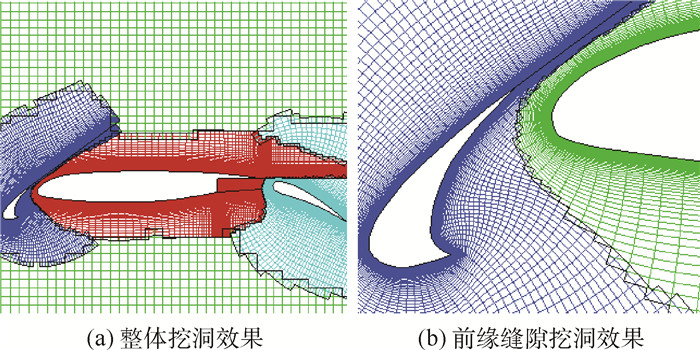
1) 二维30P30N三段翼型。首先以30P30N三段翼型作为二维算例考核结构重叠网格的挖洞效果。30P30N翼型的原始网格为5块结构网格,总网格数6.986万。挖洞结果如图 10所示。
2) 三维直机翼-带舵导弹模型。本算例考查挖洞方法对三维复杂几何外形的有效性。三维直机翼-带舵弹体模型的原始网格有23块结构网格,总网格数111.72万。挖洞结果如图 11所示。
本节所选外形具有以下几何特征:30P30N翼型带有尖后缘和细缝,而直机翼-带舵导弹模型除机翼具有尖后缘外,导弹包含薄尾舵。以上挖洞结果表明,本文基于改进ADT搜索方法的挖洞处理对包含细长尾翼、细缝和细薄部件并由多块重叠结构网格组成的几何外形是有效的。
3.3 数值计算和应用验证
以下通过基于重叠网格的数值模拟再次检验网格装配方法和改进ADT搜索方法的可靠性。其中,Navier-Stoker方程的求解基于本文作者所发展的ACANS有限差分CFD程序, 该程序的可靠性已经过大量算例验证[15-16]。在本文的数值模拟中,无黏通量采用AUSMDV格式[25],同时使用MUSCL方法[26]提高空间离散的精度;黏性通量采用中心差分格式;时间推进采用隐式LU-SGS方法[27];湍流计算主要选取k-ω SST模型[28]。另外,为满足重叠网格数值计算的需要,插值区域采用双/三线性插值方法[10]传递流场信息。为加快计算速度和适应大规模计算的需要,ACANS采用了基于MPI(Message Passing Interface)技术的空间分解并行算法。
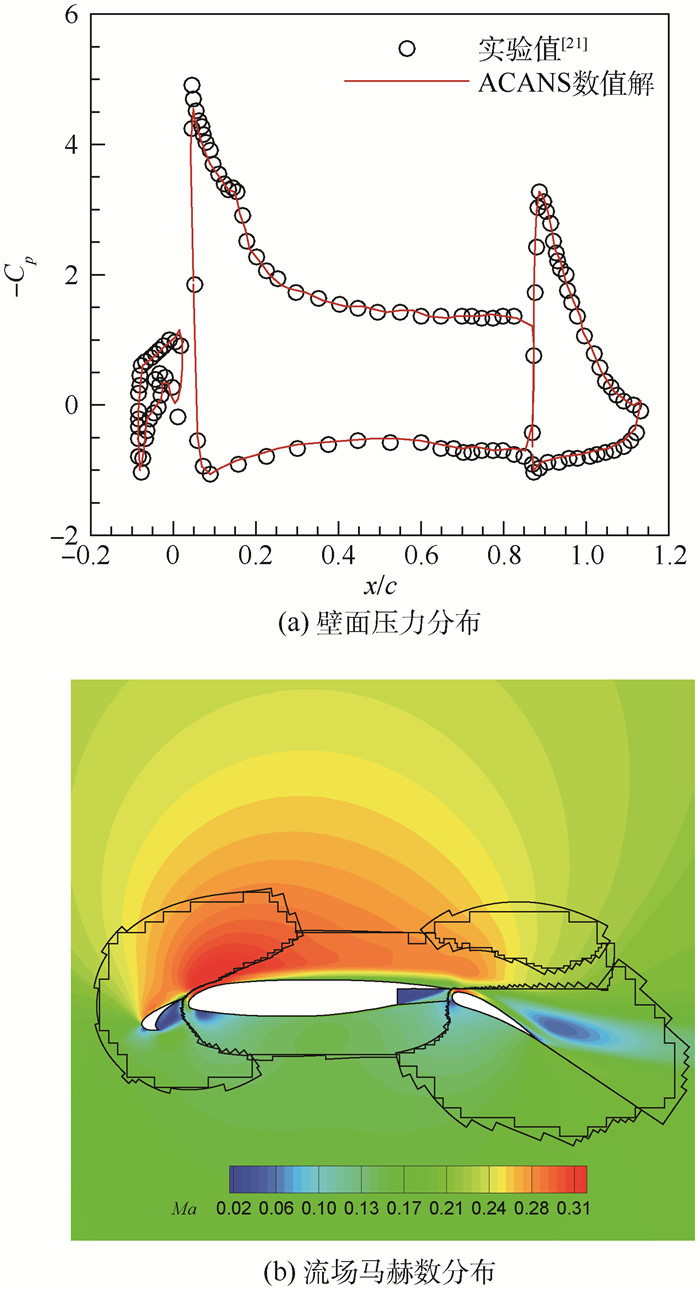
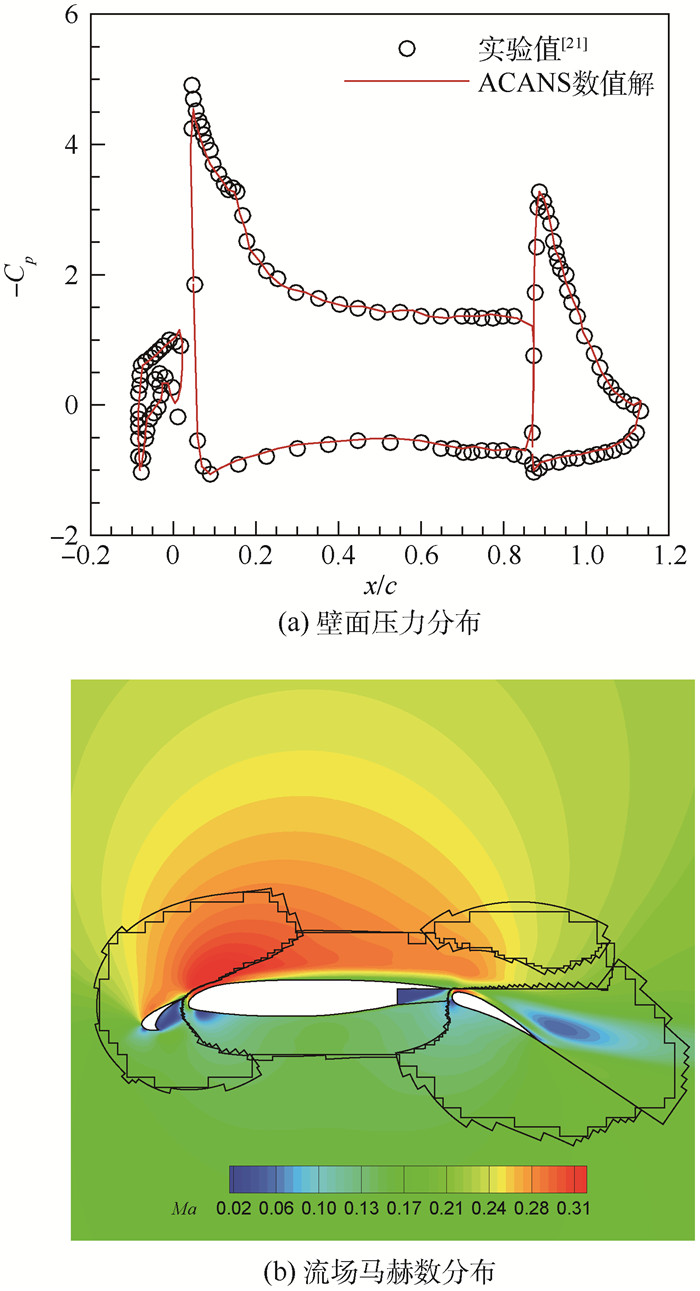
算例1 30P30N翼型低速绕流。计算网格如图 10所示,低速绕流的计算条件为:马赫数Ma∞=0.2,迎角α=4.0°,雷诺数Re∞=9.0×106 m-1。如图 12(a)所示,数值计算得到的壁面压力分布与实验值[21]具有良好的吻合,流场马赫数分布如图 12(b)所示,其中Cp为压力系数,c为弦长。
算例2 半圆球超声速绕流。超声速流动条件为:Ma∞=2.0,压强p∞=2 325.0 Pa,Re∞=1.069×106 m-1。对比修正牛顿法的工程估算结果和基于Dragon方法的数值计算结果[22],图 13显示本文基于三维重叠网格的数值计算结果是可靠的。
算例3 直机翼-带舵导弹模型的超声速干扰流动。基于半圆球的数值验证,本算例用相同方法对直机翼-带舵导弹模型的超声速干扰流动进行数值模拟以进一步测试三维重叠网格装配结果对数值程序的适应能力。与算例2计算条件相同,采用并行方式计算,壁面和z=0截面的压强分布如图 14所示。
上述算例表明本文基于重叠网格的数值计算程序是可靠的,同时基于改进ADT搜索方法的网格装配结果满足数值程序的需要。此外,网格挖洞结果的展示和数值计算的应用从侧面证明本文发展的改进ADT搜索方法是可靠的。
4. 结论
本文引入辅助笛卡儿网格提出了一种新的基于散列数据结构的改进ADT搜索方法以弥补ADT数据结构的缺点和提高挖洞的整体效率。
本文所设计的改进ADT搜索方法为改善网格装配的整体效率提供了一种新思路,在大规模数值计算中可缓解堆栈溢出的问题。由查询深度和搜索耗时的测试结果可见,该方法减少了查询次数,提高了搜索速度,相比于现有的ADT搜索方法具有更高的搜索效率。在30P30N翼型和直机翼-带舵导弹模型的挖洞中,改进方法可使挖洞的平均效率提高25%以上。
此外,网格挖洞结果显示本文提出的改进ADT搜索方法对包含细长尾翼、细缝和细薄部件的复杂几何外形的挖洞处理是有效的。同时,数值计算和应用也证明了改进ADT搜索方法在网格装配中的可靠性。
-
表 1 30P30N翼型的搜索深度测试结果
Table 1. Test results of searching depth for 30P30N airfoil
节点编号 搜索深度/次 搜索耗时/ms 搜索耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 N1 2 884 1 120 0.312 5 0.125 0 60.00 N2 8 492 4 630 0.937 5 0.625 0 33.33 N3 14 588 9 499 1.250 0 0.937 5 25.00 表 2 直机翼-带舵导弹模型的搜索深度测试结果
Table 2. Test results of searching depth for WFS model
节点编号 搜索深度/次 搜索耗时/ms 搜索耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 N1 23 818 19 516 8.125 6.562 5 19.23 N2 46 971 22 440 15.938 7.187 5 54.90 N3 89 508 67 443 30.313 22.813 0 24.74 表 3 30P30N三段翼型的挖洞耗时
Table 3. Hole-cutting time consumption of three-element 30P30N airfoil
l 优化挖洞耗时/s 全部挖洞耗时/s 全部挖洞耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 0.01 30.640 6 18.066 4 32.156 3 18.851 6 41.38 0.02 30.625 0 18.105 5 33.871 1 19.785 2 41.59 0.05 30.714 8 18.179 7 37.152 3 21.238 3 42.83 0.10 30.898 4 18.128 9 38.796 9 21.914 1 43.52 表 4 直机翼-带舵导弹模型的挖洞耗时
Table 4. Hole-cutting time consumption of WFS model
l 优化挖洞耗时/s 全部挖洞耗时/s 全部挖洞耗时减少比例/% ADT方法 改进ADT方法 ADT方法 改进ADT方法 0.005 220.454 154.092 232.382 2 163.859 4 29.49 0.010 216.739 153.463 250.248 8 182.775 3 26.96 0.015 221.128 152.766 273.539 3 199.316 0 27.13 0.018 219.326 154.508 282.780 9 211.487 7 25.21 -
[1] 李鹏, 高振勋, 蒋崇文.重叠网格方法的研究进展[J].力学与实践, 2014, 36(5):551-565. doi: 10.6052/1000-0879-14-011LI P, GAO Z X, JIANG C W.Progress of the overlapping grid techniques[J].Mechanics in Engineering, 2014, 36(5):551-565(in Chinese). doi: 10.6052/1000-0879-14-011 [2] PREWITT N, BELK D, SHYY W.Parallel computing of overset grids for aerodynamic problems with moving objects[J].Progress of Aerospace Science, 2000, 36(2):117-172. doi: 10.1016/S0376-0421(99)00013-5 [3] BLANC F.Patch assembly:An automated overlapping grid assembly strategy[J].Journal of Aircraft, 2010, 47(1):110-119. doi: 10.2514/1.44116 [4] MEAKING R L.A new method for establishing intergrid communication among systems of overset grids:AIAA-1991-1586[R].Reston:AIAA, 1991. [5] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社, 2006:200-208.YAN C.Computational fluid dynamics methods and applications[M].Beijing:Beihang University Press, 2006:200-208(in Chinese). [6] 张来平, 邓小刚, 张涵信.动网格生成技术及非定常计算方法进展综述[J].力学进展, 2010, 40(4):424-447. doi: 10.6052/1000-0992-2010-4-J2009-123ZHANG L P, DENG X G, ZHANG H X.Reviews of moving grid generation techniques and numerical methods for unsteady flows[J].Advances in Mechanics, 2010, 40(4):424-447(in Chinese). doi: 10.6052/1000-0992-2010-4-J2009-123 [7] 田书玲. 基于非结构网格方法的重叠网格算法研究[D]. 南京: 南京航空航天大学, 2008: 43-74.TIAN S L.Study of overset grids methods based on unstructured grids[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2008:43-74(in Chinese). [8] BONET J, PERAIRE J.An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems[J].International Journal for Numerical Methods in Engineering, 1991, 31(1):1-17. doi: 10.1002/(ISSN)1097-0207 [9] BROWN R A.Building a balanced k-d tree in O(kn log n) time[J].Journal of Computer Graphics Techniques, 2015, 4(1):50-68. [10] MARSTIN C W, MCCONNAUGHEY H V.Computational problems on composite grids:AIAA-1984-1611[R].Reston:AIAA, 1984. [11] BELK D M, MAPLE R C.Automated assembly of structured grids for moving body problems:AIAA-1995-1680[R].Reston:AIAA, 1995. [12] 袁武, 阎超, 于剑, 等.基于虚网格的格心ADT搜索法[J].北京航空航天大学学报, 2012, 38(10):1375-1379.YUAN W, YAN C, YU J, et al.Cell-center ADT algorithm based on ghost cell[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10):1375-1379(in Chinese). [13] 刘鑫, 陆林生.重叠区域找重策略和插值方法的研究[J].计算机应用研究, 2006, 23(7):26-28. http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ200607006.htmLIU X, LU L S.Research on intersection strategies and interpoiation methods of overset zone[J].Application Research of Computers, 2006, 23(7):26-28(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ200607006.htm [14] 袁武. 新型重叠网格方法研究及其在复杂多体气动问题中的应用[D]. 北京: 北京航空航天大学, 2013: 36-49.YUAN W.Investigations on novel Chimera grid methods and its applications to complex multibody aerodynamic problems[D].Beijing:Beihang University, 2013:36-49(in Chinese). [15] GAO Z X, JIANG C W, LEE C H.Improvement and application of a wall function boundary condition for high-speed compressible flows[J].Science China Technological Science, 2013, 56 (10):2501-2515. doi: 10.1007/s11431-013-5349-4 [16] GAO Z X, LEE C H.Numerical research on mixing characteristics of different injection schemes for supersonic transverse jet[J].Science China Technological Science, 2011, 54(4):883-893. doi: 10.1007/s11431-010-4277-9 [17] XU J, CAI J S, LIU Q H, et al.Flow simulations by enhanced implicit-hole-cutting method on overset grids[J].Journal of Aircraft, 2014, 51(5):1401-1409. doi: 10.2514/1.C032283 [18] WANG Z J.A Conservative overlapped (Chimera) grid algorithm for multiple moving body flows[C]//AIAA 34th Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 1996. [19] CHIU I T, MEAKIN R L.On automating domain connectivity for overset grids:AIAA-1995-0854[R].Reston:AIAA, 1995. [20] WEY T C.Development of a mesh interface generator for overlapped structured grids:AIAA-1994-1924[R].Reston:AIAA, 1994. [21] CHO K W, KWON J H.Development of a fully systemized Chimera methodology for steady/unsteady problems[J].Journal of Aircraft, 1999, 36(6):973-980. doi: 10.2514/2.2538 [22] LEE Y L, BAEDER J D.Implicit hole cutting-A new approach to overset grid connectivity:AIAA-2003-4128[R].Reston:AIAA, 2003. [23] MAPLE R C, BELK D M.A new approach to domain decomposition——The beggar code:in numerical grid generation in computational fluid dynamics and related fields[M].Landshut:Pine Ridge Press, 1994:305-314. [24] NIRSCHL H, DWYER H A, DENK V.A Chimera grid scheme for the calculation of particle flows:AIAA-1994-0519[R].Reston:AIAA, 1994. [25] WADA Y, LIOU M S.An accurate and robust flux splitting scheme for shock and contact discontinuities[J].SIAM Journal of Science Computer, 1997, 18(3):633-657. doi: 10.1137/S1064827595287626 [26] VAN LEER B.Towards the ultimate conservative difference scheme Ⅴ:A second order sequel to Godunov's method[J].Journal of Computer Physics, 1979, 32(1):101-136. doi: 10.1016/0021-9991(79)90145-1 [27] YOON S, JAMESON A.Lower-upper symmetric Gauss-Sediel method for the Euler and Navier-Stoker equations[J].AIAA Journal, 1988, 26(9):1025-1026. doi: 10.2514/3.10007 [28] MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal, 1994, 32(8):1598-1605. doi: 10.2514/3.12149 -








 下载:
下载:













 下载:
下载: