长时间流固耦合传热过程的快速算法

孟繁超; 董素君; 江泓升; 王浚

doi:10.13700/j.bh.1001-5965.2016.0447

长时间流固耦合传热过程的快速算法

doi: 10.13700/j.bh.1001-5965.2016.0447

北京航空航天大学航空科学与工程学院, 北京 100083

详细信息

作者简介:
孟繁超,男, 硕士研究生。主要研究方向:流场温度场数值仿真技术

董素君,女, 教授, 硕士生导师。主要研究方向:飞行器环境控制系统仿真及CFD数值计算技术、飞行器综合环境控制及热管理技术、高超声速飞行器气动热环境模拟技术

通讯作者:
董素君, E-mail: dsj@buaa.edu.cn

中图分类号: TK124
计量
- 文章访问数: 1065
- HTML全文浏览量: 238
- PDF下载量: 535
- 被引次数: 0
出版历程
- 收稿日期: 2016-05-24
- 录用日期: 2016-10-14
- 网络出版日期: 2017-06-20

A fast algorithm for long-term fluid-solid conjugate heat transfer process

School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

More Information

Corresponding author: DONG Sujun, E-mail:dsj@buaa.edu.cn

摘要

摘要:
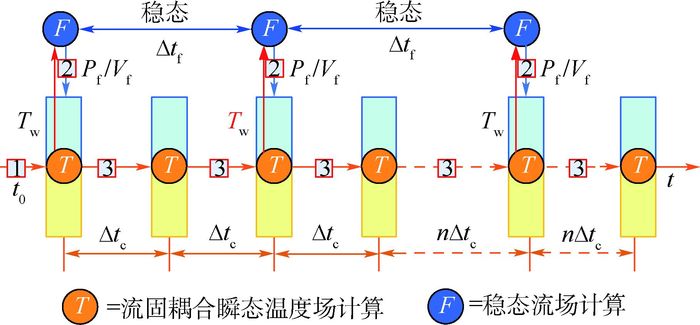
针对千秒级长时间流固耦合传热（CHT）过程求解问题，进一步提出一种基于准稳态流场的全局瞬态紧耦合传热的新型松耦合算法。交替使用单独对流体区域进行稳态流场求解的算法更新流场，以及同时对流固区域进行瞬态传热求解的算法计算瞬态温度场。该算法相对于传统流固松耦合算法，可以大大减小流场更新频率，进一步显著提高计算效率。以管内定来流速度空气连续300 s的强制对流瞬态加热过程为例，利用Fluent软件证明了该算法相对于瞬态紧耦合算法获得的管体结构温升最大偏差为5%，而计算耗时减小到14.8%。
- 流固耦合传热 /
- 松耦合 /
- 准稳态 /
- 计算流体力学(CFD) /
- 强制对流
Abstract:
Concerning the specific demands for solving problems of the long-term conjugate heat transfer (CHT) problem at the kilosecond level, a new loosely coupled algorithm of the global tightly transient coupled heat transfer based on the quasi-steady flow field is put forward. The flow field is updated alone by steady algorithm and the transient temperature field of the fluid and solid regions are solved by transient heat transfer algorithm alternately. Compared to the traditional loosely coupled algorithm, the computational efficiency is further improved with the greatly reduced update frequency of the flow field. Taking a tube heated by inner forced air flow heating process for 300 s as an example, the results by Fluent software show that, compared to the tightly transient coupled calculation, the maximum wall temperature rise deviation is 5% while the computing time is reduced to 14.8%.
- fluid-solid conjugate heat transfe /
- loosely coupled /
- quasi-steady /
- computational fluid dynamics (CFD) /
- forced convection

HTML全文

图 1 新型松耦合算法流程示意图

T—温度; P_f—流体压力; V_f—流体速度; Δt_f—稳态流场更新步长; Δt_c—瞬态时间步长; n—瞬态迭代步数; T_w—壁面温度

Figure 1. Flow diagram of new loosely coupled algorithm

下载: 全尺寸图片幻灯片

图 2 空气内加热管几何模型

Figure 2. Geometric model of inner-air-heated tube

下载: 全尺寸图片幻灯片

图 3 管内不同位置处空气静压变化曲线

Figure 3. Changing curves of inner air staticpressure at different locations

下载: 全尺寸图片幻灯片

图 4 2种算法所得不同位置管体温升、温升绝对偏差及温升相对偏差变化曲线

Figure 4. Changing curves of wall temperature rise, absolutedeviation of wall temperature rise and relative deviation ofwall temperature rise at different locations by two algorithms

下载: 全尺寸图片幻灯片

图 5 2种算法所得不同时刻管体温升分布对比曲线

Figure 5. Contrast curves of wall temperature rise distribution at different moments by two algorithms

下载: 全尺寸图片幻灯片

图 6 定来流工况下，管内壁热流随时间变化曲线

Figure 6. Curve of inner wall heat flux variation with time under constant flow rate condition

下载: 全尺寸图片幻灯片

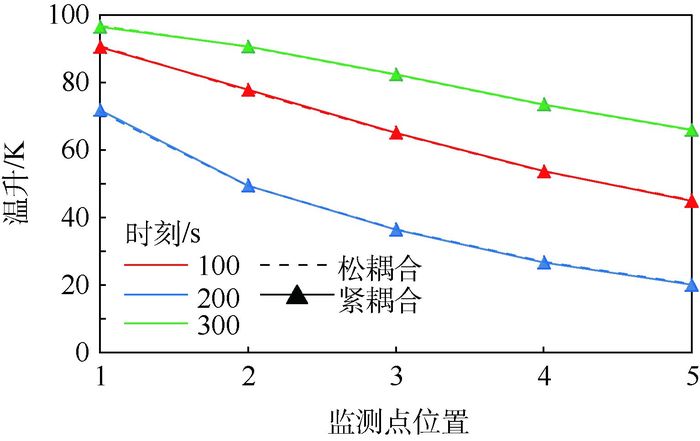
表 1 2种算法所得不同时刻管体温升分布情况

Table 1. Wall temperature rise distribution at different moments by two algorithms

K
时刻/s	位置1			位置2			位置3			位置4			位置5
时刻/s	紧耦合	松耦合	偏差	紧耦合	松耦合	偏差	紧耦合	松耦合	偏差	紧耦合	松耦合	偏差	紧耦合	松耦合	偏差
100	71.79	71.24	-0.55	49.43	49.38	-0.05	36.43	36.53	0.10	26.72	26.84	0.12	20.09	20.37	0.28
200	90.41	90.78	0.37	77.80	77.46	-0.34	65.10	64.89	-0.21	53.68	53.61	-0.07	44.95	45.08	0.13
300	96.45	96.79	0.34	90.62	90.57	-0.05	82.36	82.20	-0.16	73.44	73.28	-0.16	65.93	65.80	-0.13

下载: 导出CSV

参考文献(15)

[1]	STOKOS K, VRAHLIOTIS S, PAPPOU T, et al.Development and validation of an incompressible Navier-Stokes solver including convective heat transfer[J].International Journal of Numerical Methods for Heat & Fluid Flow, 2015, 25(4):861-886. https://www.researchgate.net/publication/276532443_Development_and_validation_of_an_incompressible_Navier-Stokes_solver_including_convective_heat_transfer
[2]	HOOPER R W, SMITH T M, OBER C C.Enabling fluid-structural strong thermal coupling within a multi-physics environment[C]//44th AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2006:1-10.
[3]	KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H.Analysis and application of high order implicit Runge-Kutta schemes for unsteady conjugate heat transfer:A strongly-coupled approach[J].Journal of Computational Physics, 2014, 272:471-486. doi: 10.1016/j.jcp.2014.04.016
[4]	曾大文, 黄开金.非交错网格下三维准稳态激光重熔熔池数值模拟[J].计算物理, 1999, 16(6):616-623. http://www.cnki.com.cn/Article/CJFDTOTAL-JSWL199906010.htm ZENG D W, HUANG K J.Numerical simulation of three dimensional quasi-steady state laser melted pools on the non-staggered grids[J].Chinese Journal of Computational Physics, 1999, 16(6):616-623(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSWL199906010.htm
[5]	殷鹏飞, 张蓉, 熊江涛, 等.搅拌摩擦焊准稳态温度场数值模拟[J].西北工业大学学报, 2012, 30(4):622-627. http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201204031.htm YIN P F, ZHANG R, XIONG J T, et al.An effective numerical simulation of temperature distribution of friction stir welding in quasi-steady-state[J].Journal of Northwestern Polytechnical University, 2012, 30(4):622-627(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-XBGD201204031.htm
[6]	BAUMAN P T, STOGNER R, CAREY G F, et al.Loose-coupling algorithm for simulating hypersonic flows with radiation and ablation[J].Journal of Spacecraft and Rockets, 2011, 48(1):72-80. doi: 10.2514/1.50588
[7]	KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H.A high order time-accurate loosely-coupled solution algorithm for unsteady conjugate heat transfer problems[J].Computer Methods in Applied Mechanics and Engineering, 2013, 264:205-217. doi: 10.1016/j.cma.2013.05.021
[8]	KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H.Accuracy and stability analysis of a second-order time-accurate loosely coupled partitioned algorithm for transient conjugate heat transfer problems[J].International Journal for Numerical Methods in Fluids, 2014, 74(2):113-133. doi: 10.1002/fld.v74.2
[9]	LOHNER R, YANG C, CEBRAL J, et al.Fluid-structure-thermal interaction using a loose coupling algorithm and adaptive unstructured grids[C]//Proceedings of 29th AIAA Fluid Dynamics Conference.Reston:AIAA, 1998:1-16.
[10]	LI Q, LIU P, HE G.Fluid-solid coupled simulation of the ignition transient of solid rocket motor[J].Acta Astronautica, 2015, 110:180-190. doi: 10.1016/j.actaastro.2015.01.017
[11]	MILLER B A, CROWELL A R, MCNAMARA J J.Loosely coupled time-marching of fluid-thermal-structural interactions:AIAA-2013-1666[R].Reston:AIAA, 2013.
[12]	KONTINOS D.Coupled thermal analysis method with application to metallic thermal protection panels[J].Journal of Thermophysics and Heat Transfer, 1997, 11(2):173-181. doi: 10.2514/2.6249
[13]	CHEN Y K, MILOS F S, GOKCEN T.Loosely coupled simulation for two-dimensional ablation and shape change[J].Journal of Spacecraft & Rockets, 2010, 47(5):775-785. https://www.researchgate.net/publication/241306596_Loosely_Coupled_Simulation_for_Two-Dimensional_Ablation_and_Shape_Change
[14]	ZHANG S, CHEN F, LIU H.Time-adaptive, loosely coupled strategy for conjugate heat transfer problems in hypersonic flows[J].Journal of Thermophysics and Heat Transfer, 2014, 28(4):1-12. https://www.researchgate.net/publication/269786163_Time-Adaptive_Loosely_Coupled_Strategy_for_Conjugate_Heat_Transfer_Problems_in_Hypersonic_Flows
[15]	AMES W F.Numerical methods for partial differential equations[M].2nd ed. New York:Academic Press, 1977:114, 116-117, 145-151.