超高速流动模拟及热化学反应模型对比研究

周凯; 李旭东; 胡宗民; 姜宗林

doi:10.13700/j.bh.1001-5965.2016.0474

超高速流动模拟及热化学反应模型对比研究

doi: 10.13700/j.bh.1001-5965.2016.0474

1.
中国科学院力学研究所高温气体动力学国家重点实验室, 北京 100190
2.
北京航天长征飞行器研究所, 北京 100076

基金项目:

国家自然科学基金 11532014

详细信息

作者简介:
周凯, 男, 博士研究生。主要研究方向:超高速流动显示及辐射光谱测量技术

胡宗民, 男, 博士, 副研究员。主要研究方向:高超声速化学反应流动模拟

通讯作者:
胡宗民, E-mail:huzm@imech.ac.cn

中图分类号: V221⁺.3;TB553
计量
- 文章访问数: 796
- HTML全文浏览量: 95
- PDF下载量: 579
- 被引次数: 0
出版历程
- 收稿日期: 2016-06-02
- 录用日期: 2016-07-07
- 网络出版日期: 2017-06-20

Comparative study of thermal-chemical reaction models on simulation of hypervelocity flow

1.
State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
2.
Beijing Institute of Aerospace Long March Vehicle, Beijing 100076, China

Funds:

National Natural Science Foundation of China 11532014

More Information

Corresponding author: HU Zongmin, E-mail:huzm@imech.ac.cn

摘要

摘要:
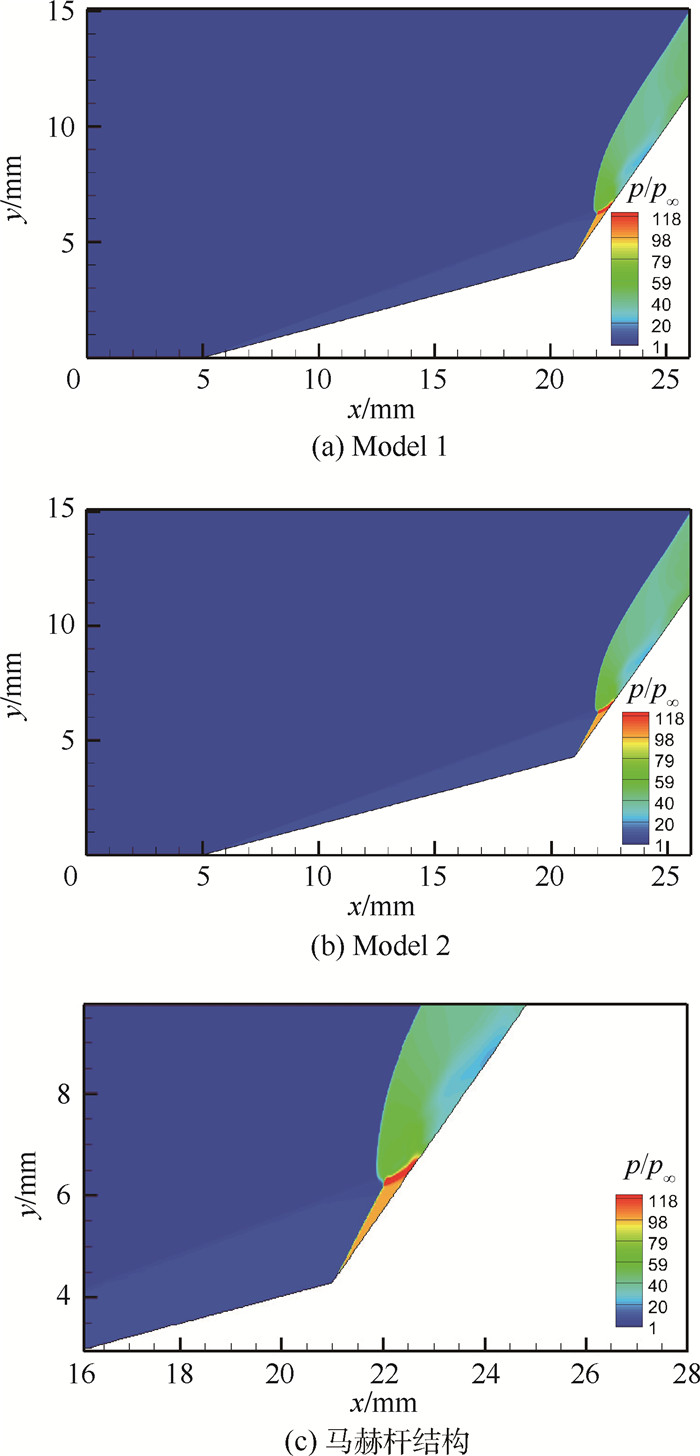
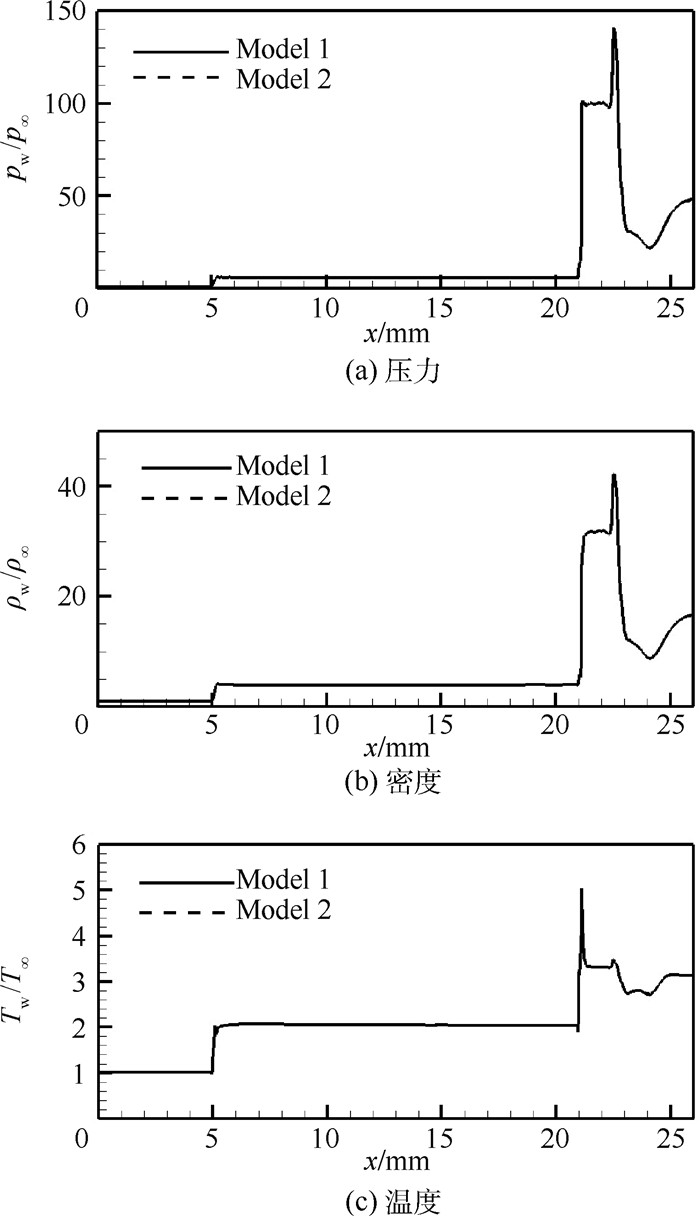
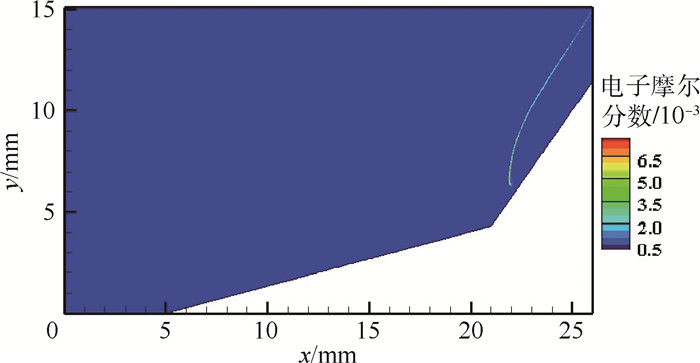
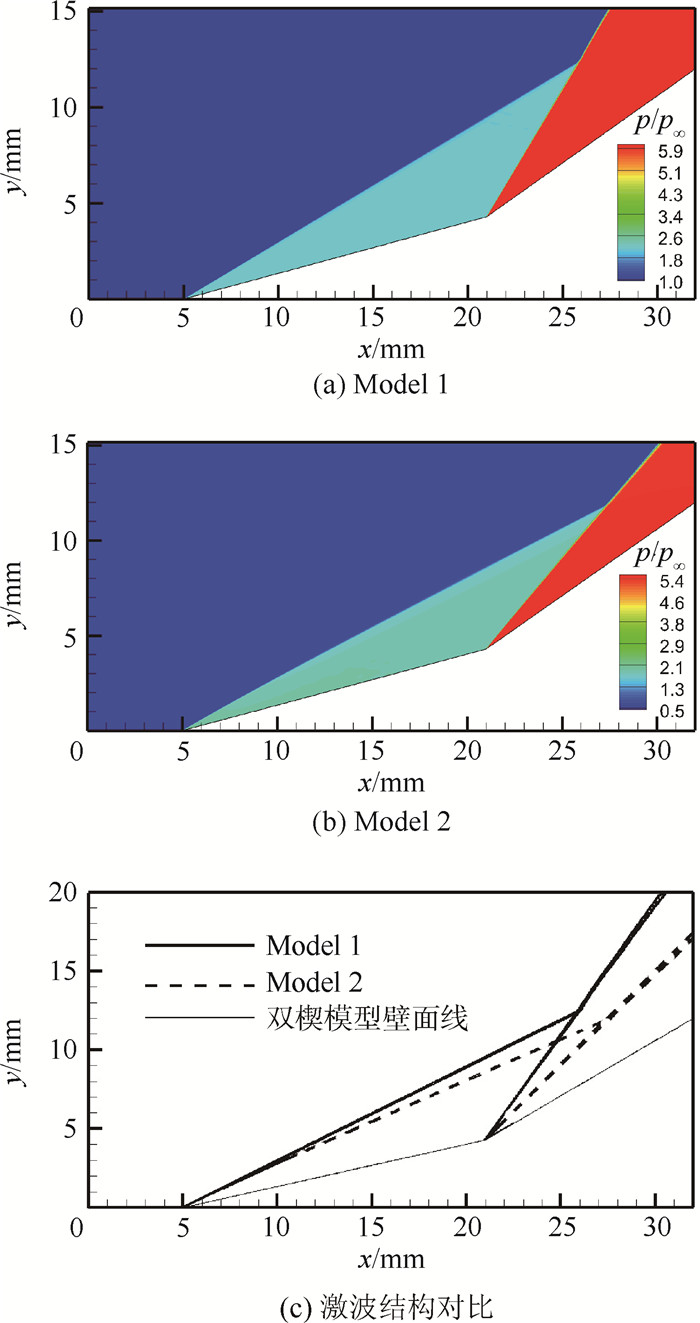
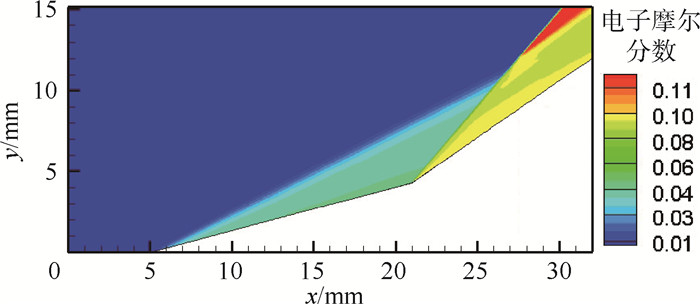
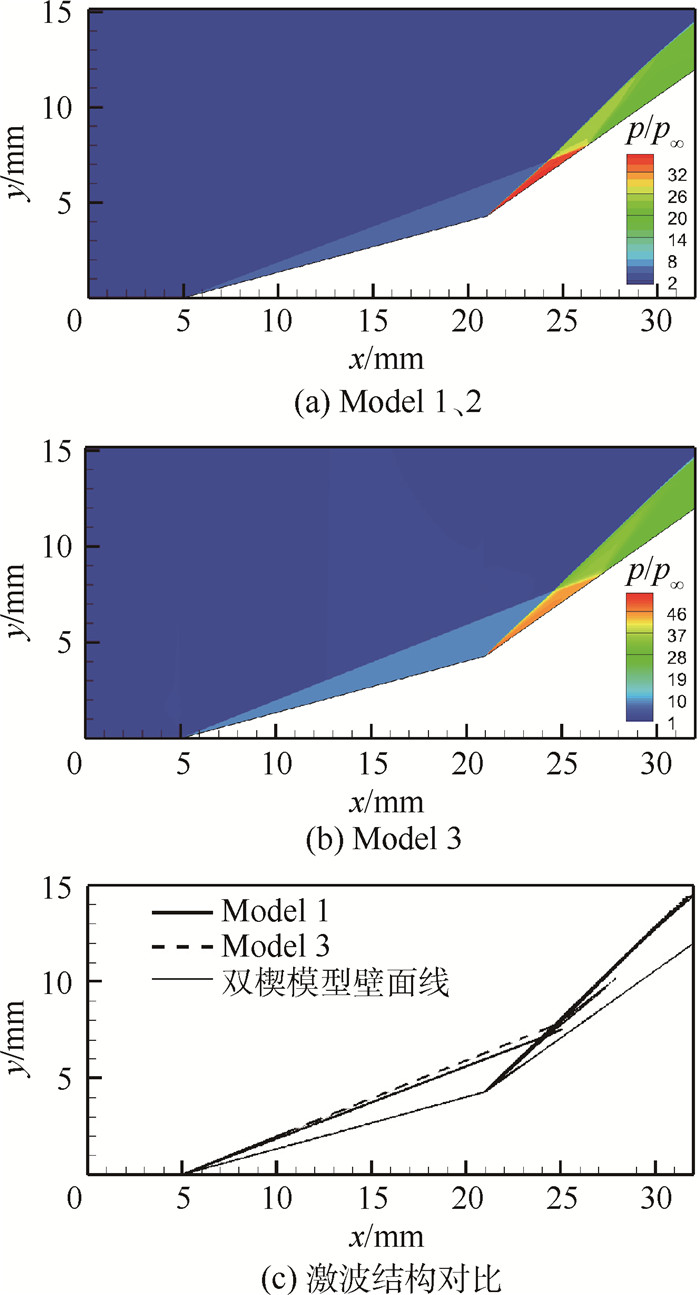
超高速流动是飞行器再入大气层时所面临的高速高温流动环境，膨胀管是少数几种能模拟超高速流动的地面设备之一。采用数值模拟方法对超高速试验进行辅助分析诊断，流动模拟时热化学反应模型的选择对流场特性影响较大，分别选择5组分、11组分热平衡及5组分热非平衡模型，对比研究3种不同热化学反应模型对双楔试验模型数值模拟结果的影响，以进一步评估超高速流动模拟时热化学反应模型的适用范围。结果表明，试验气流条件下5组分化学模型即可满足要求，加速气流条件则必须采取11组分化学模型，而对于流动中热非平衡效应显著时，热化学非平衡模型更为适用。
- 超高速 /
- 膨胀管 /
- 数值模拟 /
- 热化学反应模型 /
- 适用范围
Abstract:
Hypervelocity flow is the high-speed high-temperature flow environment that space vehicles or capsules face when they reenter the atmospheric layer. An expansion tube is one of the few qualified test facilities on the ground to simulate it. Numerical simulation is presented as a powerful assistant tool for hypervelocity flow diagnosis and analysis. Thermal-chemical reaction model plays an important role in simulation of hypervelocity flow. Thermal-chemical reaction models of 5 and 11 species based on thermal equilibrium condition, and 5 species based on thermal nonequilibrium condition are applied on the numerical technique. A comparative study of the influence on the computation for double-wedge test model employed with the above three models has been conducted to evaluate their applicability. The results indicate that 5 species chemical model can meet the test gas simulation requirement, but 11 species chemical model must be taken into account for the acceleration gas. However, if the thermal nonequilibrium phenomenon is strong in the flow, we must employ the thermal-chemical nonequilibrium model to guarantee the reliability of the numerical simulation.
- hypervelocity /
- expansion tube /
- numerical simulation /
- thermal-chemical reaction models /
- applicability

HTML全文

图 1 JF-16波动过程图

Figure 1. Sketch of wave process for JF-16

下载: 全尺寸图片幻灯片

图 2 15°~35°双楔压力分布

Figure 2. Pressure distribution of 15°~35° double-wedge

下载: 全尺寸图片幻灯片

图 3 15°~35°双楔流动参数沿壁面分布

p_w—壁面压力；ρ_w—壁面密度；ρ_∞—来流密度；T_w—壁面温度；T_∞—来流温度。

Figure 3. Flow parameter distribution along wall of 15°~35° double-wedge

下载: 全尺寸图片幻灯片

图 4 15°~35°双楔电子摩尔分数分布

Figure 4. Electronic mole fraction distribution of 15°~35° double-wedge

下载: 全尺寸图片幻灯片

图 5 15°~55°双楔压力分布

Figure 5. Pressure distribution of 15°~55° double-wedge

下载: 全尺寸图片幻灯片

图 6 15°~55°双楔流动参数沿壁面分布情况

Figure 6. Flow parameter distribution along wall of 15°~55° double-wedge

下载: 全尺寸图片幻灯片

图 7 15°~55°双楔电子摩尔分数分布

Figure 7. Electronic mole fraction distribution of 15°~55° double-wedge

下载: 全尺寸图片幻灯片

图 8 15°~35°双楔压力分布(加速气流条件)

Figure 8. Pressure distribution of 15°~35° double-wedge (acceleration gas condition)

下载: 全尺寸图片幻灯片

图 9 15°~35°双楔流动参数沿壁面分布(加速气流条件)

Figure 9. Flow parameter distribution along wall of 15°~35° double-wedge (acceleration gas condition)

下载: 全尺寸图片幻灯片

图 10 15°~35°双楔电子摩尔分数分布(加速气流条件)

Figure 10. Electronic mole fraction distribution of 15°~35° double-wedge (acceleration gas condition)

下载: 全尺寸图片幻灯片

图 11 15°~35°双楔压力分布(Model 1、2、3)

Figure 11. Pressure distribution of 15°~35° double-wedge (Model 1、2、3)

下载: 全尺寸图片幻灯片

图 12 15°~35°双楔流动参数沿壁面分布(Model 1、2、3)

Figure 12. Flow parameter distribution along wall of 15°~35° double-wedge (Model 1、2、3)

下载: 全尺寸图片幻灯片

表 1 试验气流和加速气流参数

Table 1. Flow parameters of test and acceleration gas

气流参数	u/(km·s^-1)	T/K	Ma	p/Pa	ρ/(kg·m^-3)
试验气流	8.0	2 390	7.6	9 524.550	0.011 6
加速气流	8.8	9 335	3.2	9 220.575	0.001 7
注：u—x方向速度；T—温度；Ma—马赫数；p—压力；ρ—密度。

下载: 导出CSV

表 2 Dunn & Kang高温空气化学反应模型^[20]

Table 2. Dunn & Kang chemical reaction model for air at high temperature^[20]

基元数	反应式
1	O₂+N=2O+N
2	O₂+NO=2O+NO
3	N₂+O=2N+O
4	N₂+NO=2N+NO
5	N₂+O₂=2N+O₂
6	NO⁺O₂=N⁺+O+O₂
7	NO⁺N₂=N⁺+O+N₂
8	O+NO=N⁺+O₂
9	O+N₂=N⁺+NO
10	N+N₂=2N+N
11	O₂+O=2O+O
12	O₂+O₂=2O+O₂
13	O₂+N₂=2O+N₂
14	N₂+N₂=2N+N₂
15	NO⁺O=N⁺+2O
16	NO⁺N=O₂⁺N
17	NO⁺NO=N⁺+O+NO
18	O+N=NO⁺+e^-
19	O+e^-=O⁺+2e^-
20	N+e^-=N⁺+2e^-
21	O+O=O₂⁺+e^-
22	O+O₂⁺=O₂+O⁺
23	N₂+N⁺=N⁺+N₂⁺
24	N+N=N⁺+2+e^-
25	O+NO⁺=NO⁺O⁺
26	N₂+O⁺=O+N₂⁺
27	N+NO⁺=NO⁺N⁺
28	O₂+NO⁺=NO⁺O₂⁺
29	O+NO⁺=O₂+N⁺
30	O₂+N₂=NO⁺NO⁺+e^-
31	NO⁺N₂=NO⁺+N₂+e^-

下载: 导出CSV

表 3 15°~35°双楔粒子摩尔分数峰值

Table 3. Max mole fraction of species for 15°~35° double-wedge

粒子	摩尔分数峰值
N	0.34
O	0.33
NO	0.04
N⁺	6.31×10^-5
O⁺	5.08×10^-4
NO⁺	4.74×10^-4
e^-	1.06×10^-3

下载: 导出CSV

表 4 15°~55°双楔粒子摩尔分数峰值

Table 4. Max mole fraction of species for 15°~55° double-wedg

粒子	摩尔分数峰值
N	0.69
O	0.31
NO	0.03
N⁺	1.73×10^-2
O⁺	6.37×10^-2
NO⁺	6.29×10^-3
e^-	7.66×10^-2

下载: 导出CSV

表 5 15°~35°双楔粒子摩尔分数峰值(加速气流条件)

Table 5. Max mole fraction of species for 15°~35° double-wedge (acceleration gas condition)

粒子	摩尔分数峰值
N	0.77
O	0.21
NO	6.88×10^-5
N⁺	0.11
O⁺	0.05
NO⁺	3.55×10^-4
e^-	0.13

下载: 导出CSV

参考文献(21)

[1]	ANDERSON J D.Hypersonic and high temperature gas dynamics[M].New York:McGraw-Hill Book Company, 2006:449-461.
[2]	NEELY A J, MORGAN R G.The superorbital expansion tube concept, experiment and analysis[J].Aeronautical Journal, 1994, 98(973):97-105. doi: 10.1017/S0001924000050107
[3]	HORNUNG H G.Experimental hypervelocity flow simulation, needs, achievements, and limitations[C]//Proceedings of 1st Pacific International Conference on Aero-space Science and Technology.Tainan:National Cheng-Kung University, 1994:1-10.
[4]	RESLER E L, BLOXSOM D E.Very high Mach number flows by unsteady flow principles[M].New York:Cornell University Graduate School of Aeronautical Engineering, 1952:2-7.
[5]	TRIMPI R L.A preliminary theoretical study of the expansion tube:A new device for producing high-enthalpy short-duration hypersonic gas flows:NASA-TR-R133[R].Washington, D.C.:NASA, 1962. doi: 10.1007/978-3-319-23745-9_9/fulltext.html
[6]	PAULL A, STALKER R J, STRINGER I.Experiments on an expansion tube with a free piston driver[C]//Proceedings of 15th Aerodynamic Testing Conference.Reston:AIAA, 1988:173-178.
[7]	GILDFIND D E, MORGAN R G, MCGILVRAY M, et al. Simulation of high Mach number scramjet flow conditions using the X2 expansion tube:AIAA-2012-5954[R]. Reston:AIAA, 2012.
[8]	DUFRENE A, MACLEAN M, PARKER R, et al.Experimental characterization of the LENS expansion tunnel facility including blunt body surface heating:AIAA-2011-262[R]. Reston:AIAA, 2011.
[9]	周凯, 汪球, 胡宗民, 等.爆轰驱动膨胀管性能研究[J].航空学报, 2016, 37(3):810-816. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201603007.htm ZHOU K, WANG Q, HU Z M, et al.Performance study of a detonation-driven expansion tube[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(3):810-816(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201603007.htm
[10]	HOLLIS B R, PRABHU D K.Assessment of laminar, convective aeroheating prediction uncertainties for Mars entry vehicles[J].Journal of Spacecraft and Rockets, 2013, 50(1):56-68. doi: 10.2514/1.A32257
[11]	HOLDEN M S.Development of experimental facilities coupled with CFD to research key aerothermal phenomena in hypervelocity flight[C]//Proceedings of AIAA Aerospace Planes Meeting.Reston:AIAA, 2011:243-253.
[12]	SARMA G S R.Physico-chemical modelling in hypersonic flow simulation[J].Progress in Aerospace Sciences, 2000, 36(3):281-349. https://www.researchgate.net/publication/224784512_Physico_Chemical_Modelling_in_Hypersonic_Flow_Simulation
[13]	GNOFFO P A, GUPTA R N, SHINN J L.Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium:NASA-TP-2867[R].Washington, D.C.:NASA, 1989.
[14]	LOSEV S A, MAKAROV V N, NIKOLSKY V S.Thermochemical nonequilibrium kinetic models in strong shock waves on air:AIAA-1994-1990[R].Reston:AIAA, 1994.
[15]	BUCK M L, BENSON B R, SIERON T R, et al.Aerodynamic and performance analyses of a superorbital re-entry vehicle[J].Dynamics of Manned Lifting Planetary Entry, 1963, 15(2):376-407.
[16]	PARK C.Assessment of a two-temperature kinetic model for dissociating and weakly ionizing nitrogen[J].Journal of Thermophysics and Heat Transfer, 1988, 2(1):8-16. doi: 10.2514/3.55
[17]	PARK C.The limits of two-temperature model:AIAA-2010-911[R].Reston:AIAA, 2010.
[18]	GUPTA R N, YOS J M, THOMPSON R A.A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 K:NASA-TR-1232[R].Washington, D.C.:NASA, 1989.
[19]	柳军. 热化学非平衡流及其辐射现象的实验和数值计算研究[D]. 北京: 国防科学技术大学, 2004. LIU J.Experimental and numerical research on thermo-chemical nonequilibrium flow with radiation phenomenon[D].Beijing:National University of Defense Technology, 2004(in Chinese).
[20]	DUNN M G, KANG S.Theoretical and experimental studies of reentry plasmas:NASA-CR-2232[R].Washington, D.C.:NASA, 1973.
[21]	HU Z M, WANG C, JIANG Z L, et al.On the numerical technique for the simulation of hypervelocity test flows[J].Computer and Fluids, 2015, 106:12-18. doi: 10.1016/j.compfluid.2014.09.039