基于核主成分分析的多输出模型确认方法

胡嘉蕊; 吕震宙

doi:10.13700/j.bh.1001-5965.2016.0519

基于核主成分分析的多输出模型确认方法

doi: 10.13700/j.bh.1001-5965.2016.0519

胡嘉蕊,
吕震宙^,

西北工业大学航空学院, 西安 710072

基金项目:

国家自然科学基金 51475370

中央高校基本科研业务费专项资金 3102015BJ(Ⅱ)CG009

详细信息

作者简介:
胡嘉蕊女, 硕士研究生。主要研究方向:可靠性工程、模型确认

吕震宙女, 教授, 博士生导师。主要研究方向:飞行器设计及可靠性工程

通讯作者:
吕震宙, E-mail:zhenzhoulu@nwpu.edu.cn

中图分类号: O212.4;TP391.9
计量
- 文章访问数: 887
- HTML全文浏览量: 167
- PDF下载量: 503
- 被引次数: 0
出版历程
- 收稿日期: 2016-06-15
- 录用日期: 2016-09-30
- 网络出版日期: 2017-07-20

Model validation method with multivariate output based on kernel principal component analysis

HU Jiarui,
LYU Zhenzhou^,

School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China

Funds:

National Natural Science Foundation of China 51475370

the Fundamental Research Funds for the Central Universities 3102015BJ(Ⅱ)CG009

More Information

Corresponding author: LYU Zhenzhou, E-mail: zhenzhoulu@nwpu.edu.cn

摘要

摘要:
目前对于不确定性环境下多个相关的复杂计算模型进行确认的方法存在计算困难及稳定性较差的问题。针对这类复杂计算模型，提出了一种新的基于核主成分分析（KPCA）的多输出模型确认方法。该方法将核主成分分析与面积法的思想相结合，构造了一个新的易于计算且稳定性高的模型确认指标。所提方法通过核主成分分析将相关的输出变量转化为不相关的核主成分，再对每一核主成分进行模型与实验的对比，从而避免了传统多输出模型确认方法中需要求解多个输出的联合累积分布函数的困难。由于核主成分分析（PCA）方法能够有效提取分析对象的非线性成分，因此基于核主成分分析的多输出模型确认方法较基于主成分分析的模型确认方法更为稳定，这表现在相同的实验样本数据下核主成分分析的方法具有更低的出错率。另外核主成分分析通过核主成分提取，可以实现多输出模型的降维，从而降低多输出模型确认的复杂度。所提方法既可以用于一般的多输出模型的确认，也可以用于多确认点的输出模型的确认。最后通过数值算例和工程算例证明了该方法的正确性与有效性。
- 模型确认 /
- 多输出 /
- 相关性 /
- 核主成分分析（KPCA） /
- 面积指标
Abstract:
At present, for the multiple correlated complex computational models with uncertainty, the traditional validation methods still have some problems, such as difficult calculation and poor stability.Aimed at such complex computational models, a new multivariate model validation method is proposed based on kernel principal component analysis (KPCA). By combining the KPCA with the idea of area metric, the proposed method constructs a new model validation metric which is easy to be calculated and has high stability. In proposed method, the correlated multivariate output variables are transformed into uncorrelated kernel principal component by the KPCA, and then for each kernel principal component, the computational model is compared with the experiment. Thus this method avoids the difficulties of solving the joint cumulative distribution function of multivariate output in the traditional methods. Because the KPCA can effectively extract the nonlinear characteristic of the analyzed model, the multivariate output model validation method based on the KPCA is more robust than that based on the principal component analysis (PCA). Under the same experiment sample data, the method based on the KPCA has a lower error rate than that based on PCA. Furthermore, by extracting the kernel principal component, dimensionality reduction of the multivariate output can be implemented; thereby the complexity of the multivariate output validation can also be reduced. The proposed method can be applied not only to the general multivariate output model validation, but also to the model validation with multiple validation sites. Finally, the correctness and effectiveness of the proposed method are demonstrated by the numerical and engineering examples.
- model validation /
- multivariate output /
- correlation /
- kernel principal component analysis (KPCA) /
- area metric

HTML全文

图 1 单个确认点处的面积指标

Figure 1. Area metric at single validation site

下载: 全尺寸图片幻灯片

图 2 多个确认点处的u-pooling模型确认过程

Figure 2. Validation process of u-pooling model at multiple validation sites

下载: 全尺寸图片幻灯片

图 3 基于核主成分分析的多输出模型确认指标求解流程

Figure 3. Validation metric solving flow of multivariate output model based on KPCA

下载: 全尺寸图片幻灯片

图 4 数值算例实验与模型每一核主成分的对比

Figure 4. Comparison of each kernel principal component between experiments and models of the numerical example

下载: 全尺寸图片幻灯片

图 5 汽车前轴示意图

Figure 5. Schematic of automobile front axle

下载: 全尺寸图片幻灯片

图 6 工字梁截面

Figure 6. Joist steel section

下载: 全尺寸图片幻灯片

图 7 工程算例的实验与模型每一核主成分的对比

Figure 7. Comparison of each kernel principal component between experiments and models of the engineering example

下载: 全尺寸图片幻灯片

表 1 数值算例的3个备选的计算模型

Table 1. Three alternative computational models of the numerical example

模型	公式
模型1	y₁^m1=θ₁cos(2πx₁z)+zsin x₂	θ₁=1.5
模型1	y₂^m1=sin(0.5πx₁+z)+zθ₂cosx₂	θ₂=1.5
模型2	y₁^m2=θ₁cos(2πx₁z)+zsinx₂	θ₁=1.7
模型2	y₂^m2=sin(0.5πx₁+z)+zθ₂cosx₂	θ₂=1.5
模型3	y₁^m3=θ₁cos(2πx₁z)+zsinx₂	θ₁=1.7
模型3	y₂^m3=sin(0.5πx₁+z)+zθ₂cos x₂	θ₂=1.7

下载: 导出CSV

表 2 数值算例的模型确认结果

Table 2. Model validation results of the numerical example

模型	模型1	模型2	模型3
指标值	0.012 0	0.063 6	0.101 2

下载: 导出CSV

表 3 数值算例的实验数据分别为10、100和1 000组时与10 000组模型数据确认结果对比

Table 3. Validation results of the numerical example of comparing 10, 100, 1 000 experimental observations and 10 000 model responses

指标类型	10组实验数据				100组实验数据				1 000组实验数据
	标准差			错误率/%	标准差			错误率/%	标准差			错误率/%
	模型1	模型2	模型3	错误率/%	模型1	模型2	模型3	错误率/%	模型1	模型2	模型3	错误率/%
基于PCA	0.027 9	0.025 1	0.023 4	35	0.012 7	0.014 7	0.013 5	18	0.004 4	0.006 8	0.006 6	2
基于KPCA	0.012 4	0.012 0	0.011 9	17	0.004 3	0.006 0	0.006 0	3	0.001 9	0.003 0	0.003 3	0

下载: 导出CSV

表 4 工程算例的3个备选的计算模型

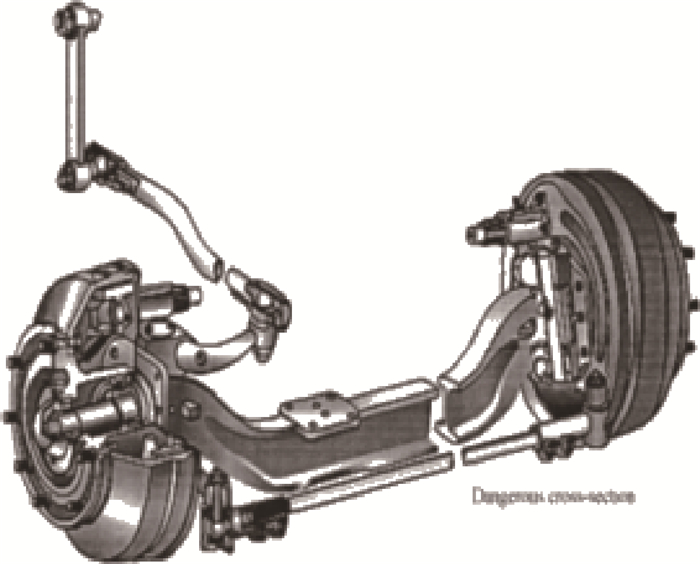
Table 4. Three alternative computational models of the engineering example

模型	公式
模型1	a=12 mm b=65 mm
模型2	a=10 mm b=65 mm
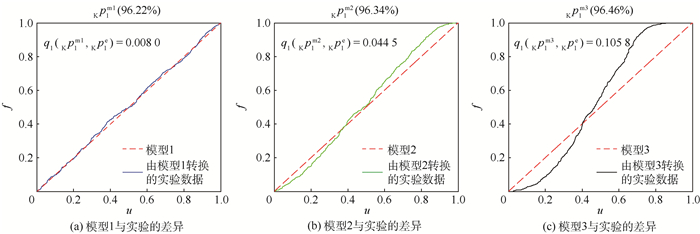
模型3	a=10 mm b=63 mm

下载: 导出CSV

表 5 工程算例的模型确认结果

Table 5. Model validation results of the engineering example

模型	模型1	模型2	模型3
指标值	0.008 0	0.044 5	0.105 8

下载: 导出CSV

参考文献(24)

[1]	OBERKANPF W L, ROY C J.Verification and validation in scientific computing[M].New York:Cambridge University Press, 2010:371-372.
[2]	郭勤涛, 张令弥, 费庆国.结构动力学有限元模型修正的发展——模型确认[J].力学进展, 2006, 36(1):36-42. doi: 10.6052/1000-0992-2006-1-J2004-142 GUO Q T, ZHANG L M, FEI Q G.From FE model updating to model validation:Advances in modeling of dynamics tructures[J].Advances in Mechanics, 2006, 36(1):36-42(in Chinese). doi: 10.6052/1000-0992-2006-1-J2004-142
[3]	刘翠翠. 建模与仿真的VV & A方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 1-2. http: //cdmd. cnki. com. cn/Article/CDMD-10217-1012518311. htm LIU C C.Research on VV & A methods of the modeling and simulation[D].Harbin:Harbin Engineering University, 2012:1-2(in Chinese). http: //cdmd. cnki. com. cn/Article/CDMD-10217-1012518311. htm
[4]	OBERKAMPF W L, SINDIR M N, CONLISK A T.Guide for the verification and validation of computational fluid dynamics simulations[M].Reston:AIAA, 1998:88-89.
[5]	OBERKAMPF W L, TRUCANO T G, HIRSCH C.Verification, validation, and predictive capability in computational engineering and physics[J].Applied Mechanics Reviews, 2004, 57(1-6):345-384. http://www.osti.gov/scitech/biblio/809603-5drfgj/native/
[6]	SCHWER L E.An overview of the PTC 60/V & V 10:Guide for verification and validation in computational solid mechanics[J].Engineering with Computers, 2007, 23(4):245-252. doi: 10.1007/s00366-007-0072-z
[7]	SORNETTE D, DAVIS A, IDE K, et al.Algorithm for model validation:Theory and applications[J].Proceedings of the National Academy of Sciences, 2007;104(16):6562-6567. doi: 10.1073/pnas.0611677104
[8]	LIU Y, CHEN W, ARENDT P, et al.Toward a better understanding of model validation metrics[J].Journal of Heat Transfer-Transactions of the ASME, 2011, 133(7):071005. doi: 10.2514/6.2010-9240
[9]	BURANATHITI T, CAO J, CHEN W, et al.Approaches for model validation:Methodology and illustration on a sheet metal flanging process[J].Journal of Manufacturing Science and Engineering-Transactions of the ASME, 2006, 128(2):588-597. doi: 10.1115/1.1807852
[10]	REBBA R, MAHADEVAN S.Validation of models with multivariate output[J].Reliability Engineering and System Safety, 2006, 91(8):861-871. doi: 10.1016/j.ress.2005.09.004
[11]	张保强, 陈国平, 郭勤涛.模型确认热传导挑战问题求解的贝叶斯方法[J].航空学报, 2011, 32(7):1202-1209. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201107006.htm ZHANG B Q, CHEN G P, GUO Q T.Solution of model validation thermal challenge problem using a Bayesian method[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(7):1202-1209(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201107006.htm
[12]	REBBA R, MAHADEVAN S.Model predictive capability assessment under uncertainty[J].AIAA Journal, 2006, 44(10):2376-2384. doi: 10.2514/1.19103
[13]	MAHADEVAN S, REBBA R.Validation of reliability computational models using Bayes networks[J].Reliability Engineering & System Safety, 2005, 87(1):223-232. https://www.researchgate.net/publication/222606257_Validation_of_reliability_computational_models_using_Bayes_networks
[14]	OBERKAMPF W L, BARONE M F.Measures of agreement between computation andexperiment:Validation metrics[J].Journal of Computational Physics, 2006, 217(1):5-36. doi: 10.1016/j.jcp.2006.03.037
[15]	OBERKAMPF W L, TRUCANO T G.Verification and validation in computational fluid dynamics[J].Progress in Aerospace Sciences, 2002, 38(2):209-272. doi: 10.1201/b19031-50
[16]	FERSON S, OBERKAMPF W, GINZBURG L.Model validation and predictive capability for the thermal challenge problem[J].Computer Methods in Applied Mechanics & Engineering, 2008, 197(29):2408-2430. https://www.researchgate.net/publication/222669317_Model_validation_and_predictive_capability_for_the_thermal_challenge_problem
[17]	LI W, CHEN W, JIANG Z, et al.New validation metrics for models with multiple correlated responses[J].Reliability Engineering & Systems Safety, 2014, 127(6):1-11. https://www.researchgate.net/publication/260156317_New_Validation_Metrics_for_Models_with_Multiple_Correlated_Responses
[18]	JOLLIFFE I T.Principal component analysis[M].Berlin:Springer-Verlag, 2002:20-24.
[19]	ANDERSON T W.An introduction to multivariate statistical analysis[M].3rd ed.New York:Wiley & Sons, 2003:47-50.
[20]	BESSE P.PCA stability and choice of dimensionality[J].Statistics & Probability Letters, 1992, 13(5):405-410. https://www.researchgate.net/profile/Philippe_Besse/publication/23631977_PCA_stability_and_choice_of_dimensionality/links/5653459b08ae4988a7af7ebf.pdf
[21]	SCHÖLKOPF B, SMOLA A, MVLLER K R.Kernel principal component analysis[J].Advances in Kernel Methods-Support Vector Learning, 2009, 27(4):555-559.
[22]	韦振中.基于核主成分分析的特征提取方法[J].广西工学院学报, 2006, 17(4):27-31. http://www.cnki.com.cn/Article/CJFDTOTAL-GXGX200604006.htm WEI Z Z.Feature extraction based on kernel principal component analysis[J].Journal of Guangxi University of Technology, 2006, 17(4):27-31(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-GXGX200604006.htm
[23]	杨胜凯. 基于核主成分分析的特征变换研究[D]. 杭州: 浙江大学, 2014: 13-24. http: //cdmd. cnki. com. cn/Article/CDMD-10335-1015578193. htm YANG S K.Research on feature transformation based on kernel principal component analysis[D].Hangzhou:Zhejiang University, 2014:13-24(in Chinese). http: //cdmd. cnki. com. cn/Article/CDMD-10335-1015578193. htm
[24]	SCHÖLKOPF B, SMOLA A, MüLLER K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation, 1998, 10(5):1299-1319. doi: 10.1162/089976698300017467