近年来，随着人们需求的增加，室内定位技术越来越受到研究人员的关注^[1-2]。超宽带(UWB)室内定位技术由于其穿透能力强、功耗低、抗多径能力强和传输速率高等特点，成为当今社会的研究热点^[3]。在室内无线定位过程中，到达时间差(TDOA)^[4]定位算法是理想的定位方法，其主要的误差来源主要是测量误差和非视距(NLOS)误差^[5]。NLOS误差^[6]是由于室内障碍物的阻隔，发生反射和折射等现象引起的，由NLOS误差引起的附加时延是定位误差的主要来源^[7]。因此NLOS误差的抑制是研究UWB室内定位首要任务。

为了抑制NLOS误差的影响，国内外已提出多种解决方案，Wylie和Holtzman^[8]提出了一种重构法，对NLOS误差进行校正，减小NLOS误差的影响，该方法需要利用视距(LOS)情况下的先验信息，在较差的环境中难以实现。Chen^[9]提出了一种残差加权法，通过对定位结果进行加权平均以减小NLOS误差影响，该方法需要较多的基站参与定位。文献[10]通过引入校正因子代入最小二乘算法，逐步迭代降低NLOS的影响，主要应用于室外环境，在室内环境中健壮性差、精度低。

本文通过对UWB信道模型IEEE 802.15.4a^[11]的仿真，分析了非视距误差对UWB室内定位的影响，利用NLOS环境下信号的传播时延特性，由概率论知识估计附加时延的均值与方差^[12]，修正测量值，根据修正后的数据，利用Chan算法与粒子群算法相结合的协同定位算法进行定位，该算法在抑制NLOS误差的同时，提高了室内定位精度，满足定位的要求，而且Chan算法与粒子群算法在无线传感器网络定位中都有着广泛的应用，因此协同定位算法适用于实际应用中。

1.   定位算法

TDOA定位算法是通过测量2个基站到达目标位置的传播时间差来确定目标位置，由时间差可以得到1条以2个基站为焦点的双曲线，因此只需2组时间差值，得到2条双曲线，其交点就是待测目标位置^[13]。

1.1   Chan算法

Chan算法^[14]是一种具有解析表达式的典型TDOA算法，在测量误差较小的情况下可达到克拉美罗下界(CRLB)。设定位目标位置坐标为(x，y)，第i个基站坐标为(x_i，y_i)，基站到目标位置的距离为d_i，第1个基站与第i个基站到目标位置的距离差为d_{i, 1}，由此可以得到

式中：K_i=x_i²+y_i²。由于

式中：x_{i, 1}=x_i－x₁; y_{i, 1}=y_i－y₁。非线性方程组就变成了线性方程组，求出方程组中的x、y值就求得目标位置坐标。令z_a=[z_p^T, R₁]，z_p=[x, y]^T，假设z_a的元素间相互独立，则z_a的最大似然估计为

式中:Ψ=E(ψψ^T)=c²BQB, B=diag{d₁⁰, d₂⁰, …, d_M⁰}，d_i⁰为d_i (i=1, 2, …，M)无噪声时的表达式，Q为TDOA的协方差矩阵，c为电磁波在空气中的传播速度。当目标位置距离较远时，d_i⁰与d⁰很接近，故B≈d⁰I，式(5) 近似为

式中：

当目标位置距离较近时，可以利用式(6) 得到一个初始值来计算矩阵B，代入式(5) 即可获得第1次加权最小二乘估计值。

利用上面得到的第1次的估计值，再重新构造误差方程组进行第2次估计得

式中:

式中：z_{a, 1}和z_{a, 2}分别为目标位置x坐标和y坐标；z_{a, 3}为第1个基站到目标位置的距离。通过2次最小二乘法得到目标位置的最终坐标为

可以看出，以上2次最小二乘估计都是基于系统测量误差服从均值为0的前提下，系统测量误差包含在该算法的加权矩阵内，因此在一定程度上消除了系统误差的影响。

1.2   粒子群算法

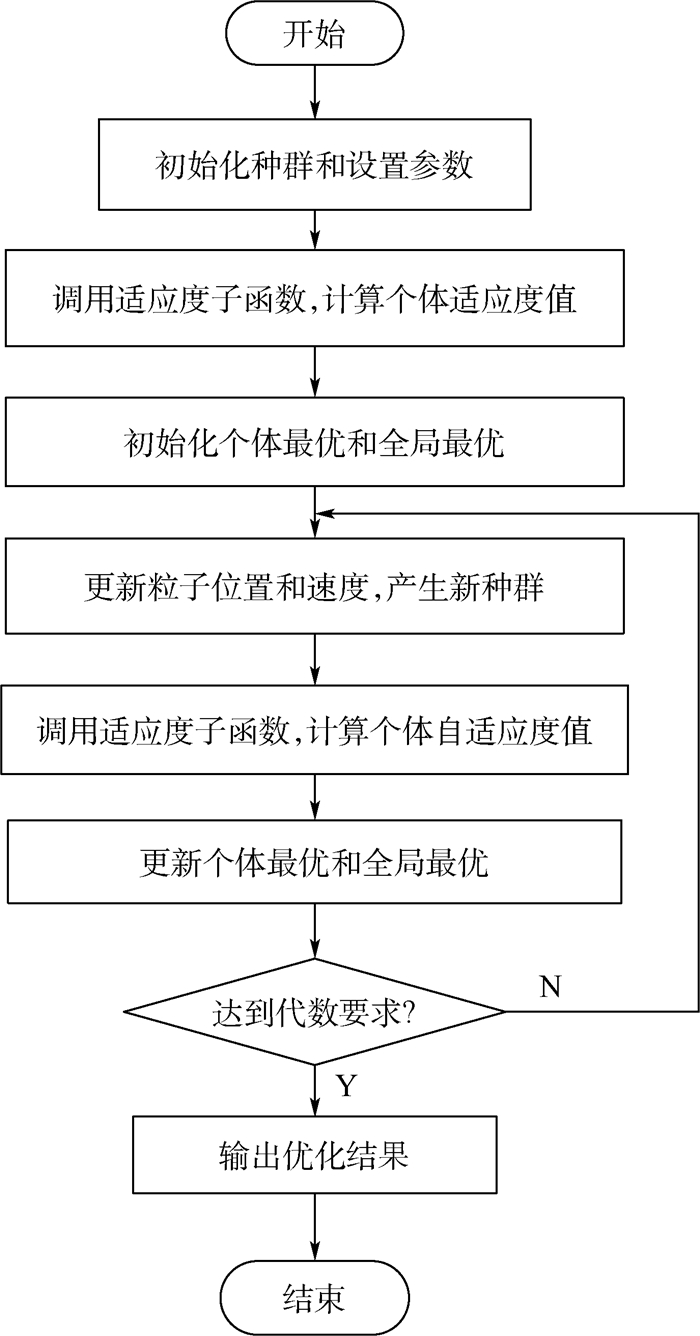
粒子群算法^[15]模仿鸟类的觅食行为，通过迭代寻优计算，能快速地找到近似解。该算法具有实现简单、精度高、收敛快等优点，在处理非线性优化问题和组合优化问题时有很好的效果^[16]，因此适用于求解TDOA非线性方程组，将双曲线方程组作为粒子群算法待优化函数，求得的最优解即为目标位置坐标。算法流程如下：

1) 初始化种群和设置参数。设定参数的运动范围，学习因子c₁、c₂，当前的进化代数k。其中第i个粒子(i=1, 2, …, S)的位置表示为X_i、速度表示为V_i，取粒子群当前最优解为B。

2) 个体适应度评价。

3) 由式(9) 和式(10) 更新粒子的速度和位置。

式中:w为惯性权重; r₁和r₂为0到1的随机数; k=1, 2, …，G；i=1, 2, …, S。

4) 计算更新后的粒子的适应度值，比较当前适应值f(X_i)与自身历史最优值p_i，如果f(X_i)较好，则置p_i为当前值f(X_i)，并更新粒子位置。

5) 比较粒子当前适应值f(X_i)与种群最优值B，如果f(X_i)优于B，则更新B的值。

6) 检查终止条件，若满足预设条件，则结束寻优；否则k=k+1，转至3)。

粒子群算法流程图如图 1所示。

图  1  粒子群算法流程图

Figure  1.  Flowchart of particle swarm algorithm

下载: 全尺寸图片 幻灯片

2.   超宽带传播信道模型

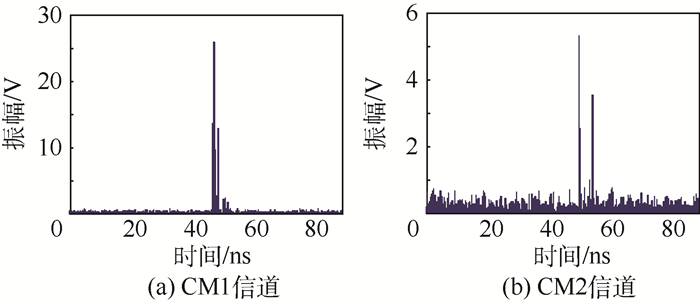
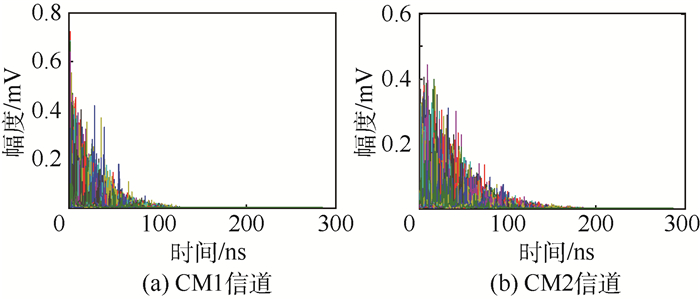
UWB通信是一种使用非常宽的频带来收发数据的技术，因此其信道特征与传统的窄带通信系统有所不同^[17]。IEEE 802.15.4 a^[11]工作小组基于诸多信道模型的建议和基于实测数据的归纳，提出了能普遍接受的信道模型，其中包括2~10 GHz的UWB信道模型，共分为4种环境：居住环境、室内办公环境、户外环境和工业环境，每种环境均分为LOS情况和NLOS情况^[18]。本文主要研究室内居住环境LOS与NLOS情况下UWB信号的传输。图 2(a)和图 2(b)分别为室内LOS(CM1) 和NLOS情况下(CM2) 信道的冲激响应。

图  2  CM1信道和CM2信道冲激响应

Figure  2.  Impulse response of CM1 channel and CM2 channel

下载: 全尺寸图片 幻灯片

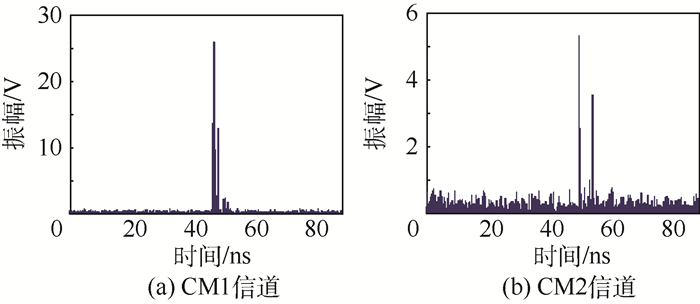
从图 2可以看出LOS情况下，首径的幅度最大，传递的能量最高，而NLOS情况下，多径幅度衰减较慢，时间弥散性强，幅度最大的径也不是第一个到达，这是由于信号在传播过程遇到障碍物发生反射和折射现象引起的。在CM1和CM2信道下，采用基于脉冲序列最大能量的到达时间测距算法，发送信号为二阶微分高斯脉冲，直接序列编码调制，发射机与接收机的实际距离为14.142 m，基于脉冲序列最大能量的到达时间测距算法能量块仿真结果如图 3所示，通过MATLAB软件仿真，测得LOS和NLOS情况下，脉冲序列最大能量值对应的时延为t₁=47.35 ns，t₂=50.15 ns，测距误差为e₁=0.062 9 m，e₂=0.902 9 m，可见，NLOS误差对于UWB信号室内传播产生了很大的影响。

图  3  CM1信道和CM2信道基于脉冲序列最大能量到达时间测距算法的能量块图

Figure  3.  Energy block diagram of maximum energy arrival time ranging algorithm based on pulse sequence of CM1 channel and CM2 channel

下载: 全尺寸图片 幻灯片

3.   非视距误差补偿

NLOS误差在不同信道下服从指数分布、均匀分布与Delta分布^[19]。本文认为其近似服从指数分布进行分析，概率密度函数为

式中:τ_{i, rms}为信道决定的均方根时延扩展，表示为τ_{i, rms}=T₁d_i^εξ，T₁为τ_{i, rms}在d_i=1 km时的中值，由IEEE 802.15.4 a^[11]信道模型仿真可得，室内NLOS环境下均方根时延扩展T₁≈19 ns，ε为0.5~1之间的一个常数, ξ表示服从均值为0、方差σ_ξ=4~6 dB的对数正态分布的随机变量。可知，ln τ_{i, rms}~N(ln(T₁d_i^ε), σ_ξ²)，可以得到τ_NLOSi的概率密度函数为

由此可计算NLOS误差的均值和方差^[20]：

在TDOA算法中，R_{i, 1}表示第1个和第i个基站到目标位置的距离差，则有

式中：, i=1, 2, …, M；τ_{i, 1}为基站1和基站i到目标位置的到达时间差^[21]。在NLOS情况下

式中：τ_{i, 1}⁰为LOS环境下的TDOA值；n_{i, 1}为系统的测量误差，服从N(0, σ_{ni, 1}²)的高斯分布；τ_{NLOSi, 1}为NLOS引起的附加时延误差，均值为μ_{NLOSi, 1}，方差为σ_{NLOSi, 1}²。

由式(13) 和式(14) 可得

可以看出τ_{NLOSi, 1}服从正均值的高斯分布，使得整体误差均值不为0，这使得定位精度受到很大影响，因此，需要对TDOA测量值进行修正：

其中n′_{i, 1}服从N(0, σ_{ni, 1}²+σ_{NLOSi, 1}²)正态分布，这样就符合Chan算法极大似然估计条件，然后将优化后的TDOA测量值代入Chan算法和粒子群算法中进行定位估计。

4.   协同定位算法

在LOS环境下，Chan算法的加权矩阵只考虑了均值为0的测量误差，2次最小二乘估计在一定程度上抵消了系统测量误差带来的影响，而NLOS误差的存在会使总体误差为正均值，也就是说位置的估计是有偏的，会使得Chan算法的定位精度有所下降。而粒子群算法求解非线性方程经过多次迭代受到NLOS误差的影响较小，计算快速准确且鲁棒性好。因此，本文提出一种在NLOS环境下改进的定位算法，即利用Chan算法与粒子群算法相结合的协同定位算法进行定位。

由于在NLOS环境下，粒子群算法优于Chan算法，因此，首先利用粒子群算法获得一个初始位置，用此初始位置修正TDOA测量值τ′_{i, 1}和系统测量的协方差Q′，Chan算法利用修正后的数据进行计算得到N组解，然后将这N组解作为粒子群算法的种群初始位置更新迭代，粒子群在更新速度和位置时，采用线性递减的时变权重^[22]，这样粒子群算法在开始时具有良好的全局搜索能力，能快速定位到近似全局最优解的区域，随着权重递减，后期具有良好的局部搜索能力，能快速找到最优解，会得到更好的算法性能。算法具体步骤如下：

1) 假设在NLOS环境下，共测得M组TDOA数据，根据基站坐标，利用粒子群算法获得一个初始估计位置。

2) 由以上初始位置计算目标位置与各基站之间的距离d_i，根据式(17) 计算μ_{NLOSi, 1}，由式(19) 计算TDOA修正值τ′_{i, 1}。

3) 根据式(18) 计算σ_{NLOSi, 1}²，重构系统测量误差的协方差Q′。

4) 根据重构后的τ′_{i, 1}和Q′，用Chan算法计算N组目标位置坐标(N≥100)。

5) 根据修正后的τ′_{i, 1}作为TDOA测量值，用粒子群算法估计目标位置，将Chan算法得到的N组数据作为粒子群算法的初始种群位置。

6) 更新粒子的位置和速度，惯性权重采用从0.90线性递减到0.10的时变权重，计算更新后的粒子适应度值，寻找最优解。

7) 检查终止条件，若满足，则停止迭代，否则重复第6) 步。

协同定位算法有两大优势：① Chan算法结果作为粒子群算法的初值，缩小了粒子群的搜索范围，加快了收敛速度；② 粒子群在更新速度和位置时，采用线性递减的时变权重，具有较好的全局搜索能力和局部搜索能力，能更快地找到最优解。因此，相比于单一算法，协同定位算法收敛速度快，定位精度高，具有更好的定位能力。

5.   仿真实验与分析

5.1   仿真条件设置

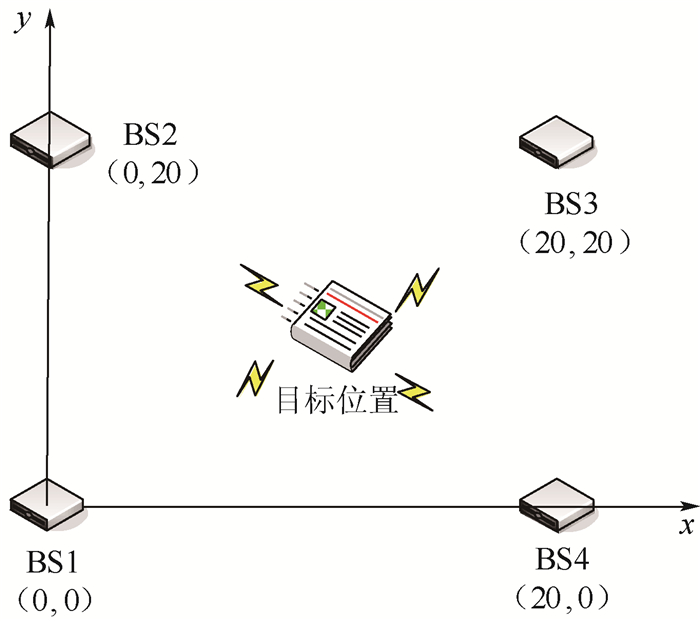
本文用MATLAB仿真工具进行算法验证，仿真采用IEEE802.15.4 a^[11]信道模型CM1和CM2，设定在一个20 m×20 m的二维空间中，存在4个基站(BS1~BS4) 和1个目标位置，目标位置真实坐标取(14.142，14.142)，其位置信息如图 4所示。

图  4  基站位置信息

Figure  4.  Location information of base station

下载: 全尺寸图片 幻灯片

误差累积分布函数(CDF)表示随机变量小于等于某个数值的概率，在此用均方根误差(RMSE)来计算误差累积分布函数，来对定位的结果进行衡量。仿真结果由100次独立估计过程得到, 均方根误差定义如下：

5.2   仿真结果与分析

5.2.1   定位精度

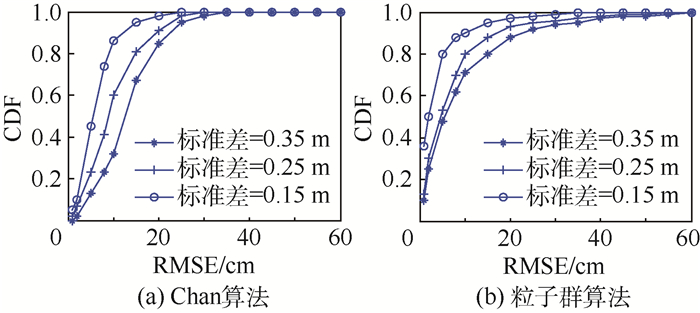
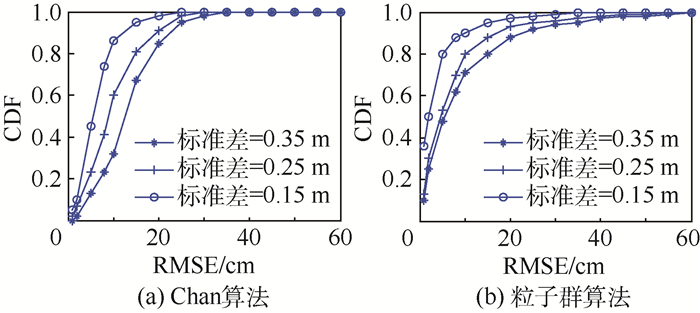
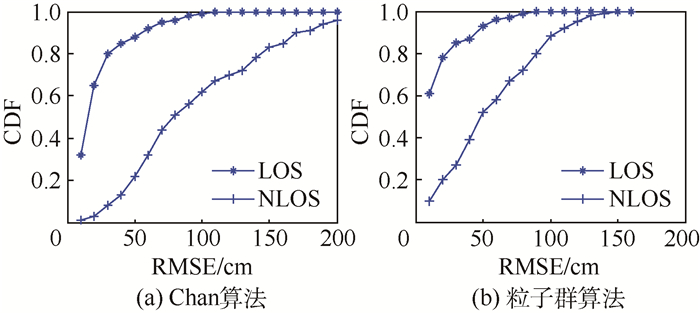
1) LOS环境下：图 5(a)和图 5(b)分别表示Chan算法和粒子群算法在LOS情况下的定位性能对比。TDOA测量值系统测量误差服从均值为0的高斯分布，在此标准差分别取0.15、0.25和0.35 m进行定位估计。从图 5中可以看出，Chan算法和粒子群算法定位精度均受到系统测量误差的影响，而且随着测量误差的增大定位误差也增大。通过图 5(a)和图 5(b)对比，可以得出，在LOS环境下，Chan算法和粒子群算法的定位结果曲线趋势大致相同，定位性能并没有很大差距。

图  5  Chan算法和粒子群算法在系统测量误差不同时的定位性能对比

Figure  5.  Comparison of positioning performance between Chan algorithm and particle swarm algorithm with different system measurement errors

下载: 全尺寸图片 幻灯片

2) NLOS环境下：图 6(a)和图 6(b)分别表示Chan算法和粒子群算法在相同的系统测量误差标准差(0.35 m)下，LOS环境与NLOS环境定位性能的对比，可以看出，NLOS误差均造成2种算法定位性能下降，且对Chan算法的影响大于粒子群算法，因此，在NLOS环境下，粒子群算法表现出更高的定位优势。

图  6  Chan算法和粒子群算法在LOS环境与NLOS环境定位性能的对比

Figure  6.  Comparison of positioning performance in LOS and NLOS environment between Chan algorithm and particle swarm algorithm

下载: 全尺寸图片 幻灯片

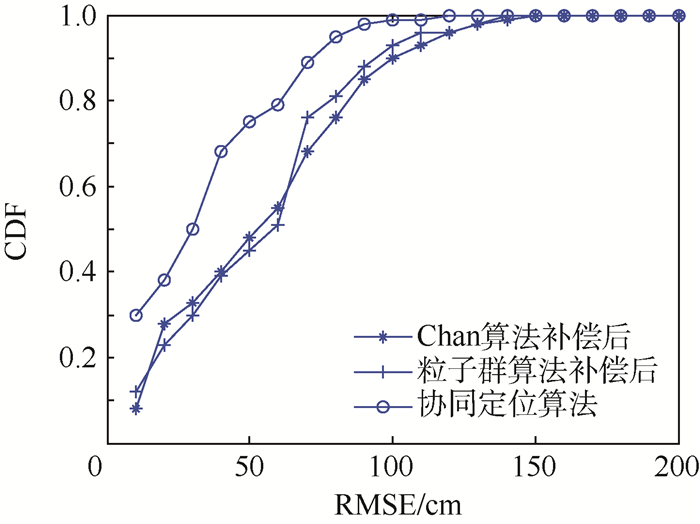
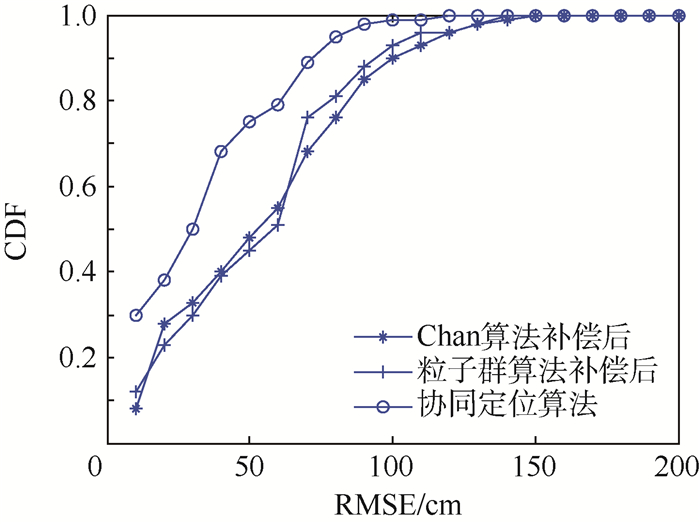
3) NLOS误差补偿后：NLOS误差的存在使得系统误差为正均值，位置的估计有偏，Chan算法的定位精度有所下降，因此协同定位算法适用于NLOS环境下。图 7表示Chan算法和粒子群算法NLOS误差补偿后和协同定位算法之间的定位性能对比。可以看出，NLOS误差补偿后Chan算法定位性能有了很大提高，这是因为TDOA的修正值是无偏的，消除了NLOS附加时延带来的误差，而粒子群算法的定位精度没有得到明显的改善。协同定位算法的定位性能明显优于2种算法补偿后的定位性能，通过计算均方根误差平均值，定位精度提高30%左右，满足室内定位的要求。

图  7  Chan算法和粒子群算法NLOS误差补偿后和协同定位算法之间的定位性能对比

Figure  7.  Comparison of positioning performance among Chan algorithm after NLOS error compensation, particle swarm algorithm after NLOS error compensation, and collaborative localization algorithm

下载: 全尺寸图片 幻灯片

5.2.2   收敛速度

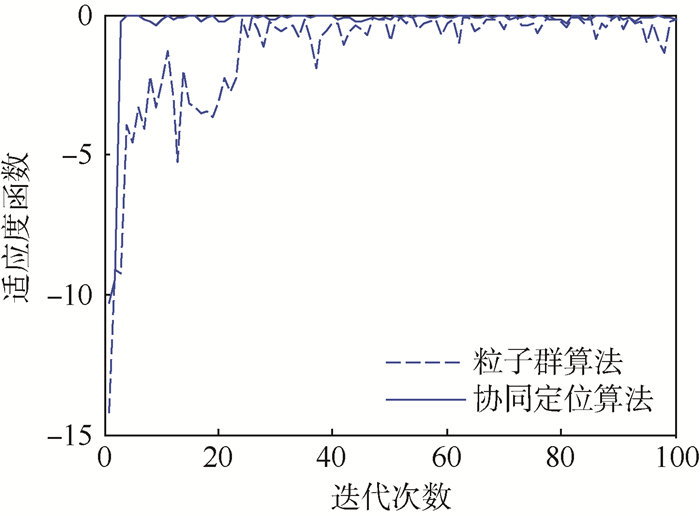
图 8表示在NLOS环境下，单一粒子群算法和协同定位算法的收敛曲线对比，可见，协同定位算法的收敛速度相比于单一粒子群算法较快，这是因为协同定位算法将NLOS误差补偿后的Chan算法结果作为粒子群算法的迭代初值，从而缩小了粒子群的搜索范围，加快了收敛速度，而且协同定位算法在更新速度和位置时，采用线性递减的时变权重，具有较好的全局搜索能力和局部搜索能力，能更快地找到最优解。

图  8  粒子群算法和协同定位算法的收敛曲线对比

Figure  8.  Comparison of convergence curves between particle swarm algorithm and collaborative localization algorithm

下载: 全尺寸图片 幻灯片

6.   结论

1) 根据NLOS环境下附加时延和由信道决定的均方根时延扩展的联合统计特性，估计NLOS误差的均值和方差，并对TDOA测量值进行修正。在此基础上，提出了一种在室内NLOS环境下，采用时变权重的粒子群算法与Chan算法相结合的协同定位算法进行UWB室内定位。

2) 在理论分析和仿真的基础上进行了实验验证。实验结果表明：在NLOS环境下，TDOA测量值修正后，协同定位算法相比于单一算法有更好的定位性能，定位精度提高30%左右，满足室内定位要求。