三波长数字相位解调法解调误差及影响因素

赵文涛; 宋凝芳; 宋镜明; 吴蓉

doi:10.13700/j.bh.1001-5965.2016.0568

三波长数字相位解调法解调误差及影响因素

doi: 10.13700/j.bh.1001-5965.2016.0568

北京航空航天大学仪器科学与光电工程学院, 北京 100083

基金项目:

国家自然科学基金 61575013

详细信息

作者简介:
赵文涛男, 硕士研究生。主要研究方向:先进光纤传感

宋凝芳女, 博士, 教授, 博士生导师。主要研究方向:先进光纤传感和空间光电技术

通讯作者:
宋镜明, E-mail: Songnf@buaa.edu.cn

中图分类号: V241.9;TN253
计量
- 文章访问数: 848
- HTML全文浏览量: 128
- PDF下载量: 629
- 被引次数: 0
出版历程
- 收稿日期: 2016-07-04
- 录用日期: 2016-08-10
- 网络出版日期: 2017-08-20

Demodulation error and influencing factor of three-wavelength digital phase demodulation method

School of Instrumentation Science and Opto-electronics Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

Funds:

National Natural Science Foundation of China 61575013

More Information

Corresponding author: SONG Jingming, E-mail: Songnf@buaa.edu.cn

摘要

摘要:
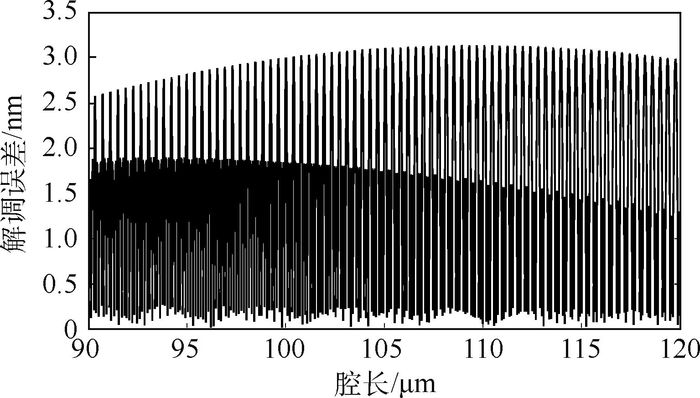
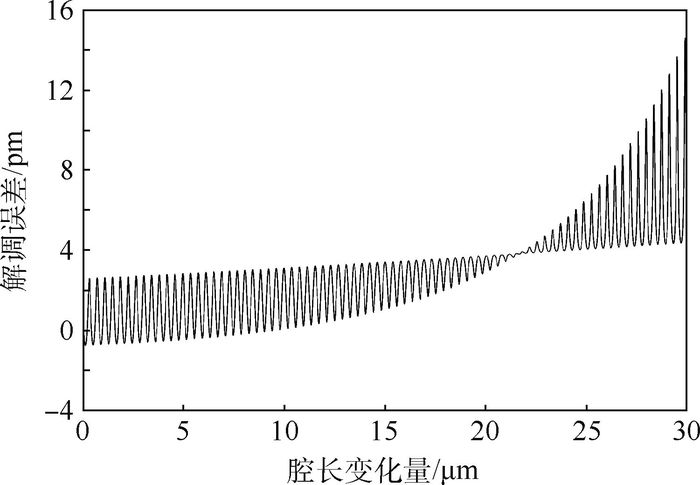
介绍了光纤法布里-珀罗（F-P）传感器的传统解调方法，系统地推导了针对非本征法布里-珀罗干涉型（EFPI）传感器解调的三波长数字相位解调法的解调原理，仿真和实验分析了三波长数字相位解调法的解调误差。仿真分析结果表明，相位偏离正交关系是限制解调的最主要因素，要保证解调误差在15 nm以内，腔长变化应小于在正交腔长处2 μm的范围。采用3个独立的激光光源进行实验，实验结果表明，在正交腔长附近1 μm范围内变化，解调腔长误差小于12 nm，重复性误差小于10 nm，解调具有良好的稳定性。
- 非本征法布里-珀罗干涉型(EFPI) /
- 三波长数字相位解调 /
- 解调误差 /
- 影响因素 /
- 稳定性
Abstract:
This paper introduces the traditional demodulation method of Fabry-Perot (F-P) sensors, and systematically derives the demodulation principle of three-wavelength digital phase demodulation method using extrinsic Fabry-Perot interferometer (EFPI) sensors. Meanwhile, simulation method has been used to analyze the demodulation error of three-wavelength phase demodulation method. The results indicate that the phase deviation from an orthogonal relationship is the most important influencing factor limiting the demodulation. In order to ensure that demodulation error is less than 15 nm, the cavity length change should be within the range of 2 μm at the orthogonal cavity length. Three independent laser light sources have been used to do the experiment. The results show that when the cavity length changes within 1 μm from orthogonal cavity length, the error of the demodulation cavity length is less than 12 nm, and at the same time the repeatability error of the demodulation is less than 10 nm, which means that demodulation has good stability.
- extrinsic Fabry-Perot interferometer (EFPI) /
- three-wavelength digital phase demodulation /
- demodulation error /
- influencing factor /
- stability

HTML全文

图 1 双波长正交法原理图^[17]

Figure 1. Schematic of two-wavelength orthogonal method^[17]

下载: 全尺寸图片幻灯片

图 2 三波长数字相位解调系统结构简图

Figure 2. Simplified structure of three-wavelength digital phase demodulation system

下载: 全尺寸图片幻灯片

图 3 相位变化与腔长关系

Figure 3. Relationship between phase variation and cavity length

下载: 全尺寸图片幻灯片

图 4 F-P干涉仪的原理

Figure 4. Principle of F-P interferometer

下载: 全尺寸图片幻灯片

图 5 实际与理论反射光强对比

Figure 5. Comparison between actual reflected light intensity and theoretical reflected light intensity

下载: 全尺寸图片幻灯片

图 6 实际与理论解调相位的对比

Figure 6. Comparison between actual demodulated phase and theoretical demodulated phase

下载: 全尺寸图片幻灯片

图 7 双光束近似引起的解调误差

Figure 7. Demodulation error caused by approximation of two beam interference

下载: 全尺寸图片幻灯片

图 8 对比度随腔长变化量的关系

Figure 8. Variation of fringe visibility factors with cavity length

下载: 全尺寸图片幻灯片

图 9 忽略对比度差异引起的解调误差

Figure 9. Demodulation error caused by ignoring differences of fringe visibility factors

下载: 全尺寸图片幻灯片

图 10 相位的正交关系

Figure 10. Orthogonal relationship of phase

下载: 全尺寸图片幻灯片

图 11 偏离相位正交关系

Figure 11. Deviation from orthogonal relationship of phase

下载: 全尺寸图片幻灯片

图 12 偏离相位正交关系引起的解调误差

Figure 12. Demodulation error caused by deviation from orthogonal relationship of phase

下载: 全尺寸图片幻灯片

图 13 标定、解调与仿真对比关系图

Figure 13. Comparison of calibration, demodulation and simulation

下载: 全尺寸图片幻灯片

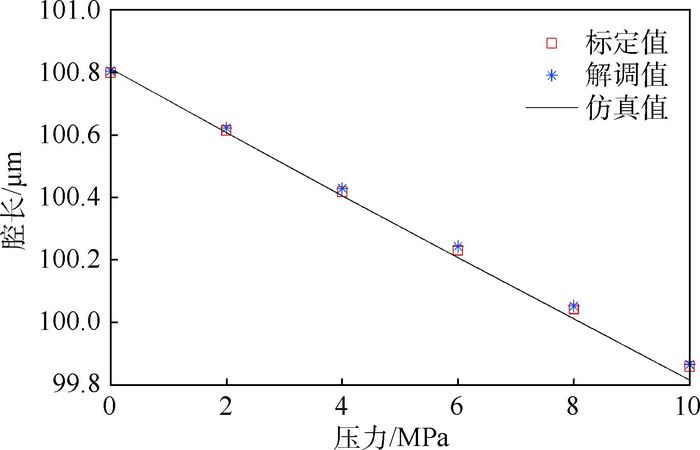
表 1 标定腔长与解调腔长对比

Table 1. Comparison between calibration cavity length and demodulation cavity length

压力/MPa 标定腔长/μm 解调腔长/μm 误差/nm

2 100.614 100.622 8

4 100.418 100.429 11

6 100.231 100.243 12

8 100.043 100.052 9

10 99.859 99.865 6

下载: 导出CSV

表 2 解调的重复性误差

Table 2. Repeatability error of demodulation value

初始压力/MPa 解调均值/μm 误差/nm

2 100.800 0

4 100.794 6

6 100.809 9

8 100.791 9

10 100.799 1

下载: 导出CSV

参考文献(18)

[1]	SEN M B, BHATIA V, MURPHY K A.Recent advances in the fiber extrinsic Fabry-Perot interferometric strain sensor development[C]//Lasers and Electro-Optics Society Meeting, 1994.Piscataway, NJ:IEEE Press, 1994, 2:253-254.
[2]	张磊, 于清旭.光纤F-P腔与FBG复用传感器精确解调方法研究[J].光电子·激光, 2009, 20(8):1008-1011. http://www.cnki.com.cn/Article/CJFDTOTAL-GDZJ200908007.htm ZHANG L, YU Q X.An improved demodulation method for F-P and FBG multiplexing system[J].Journal of Optoelectronics Laser, 2009, 20(8):1008-1011(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-GDZJ200908007.htm
[3]	李春成, 王鸣, 夏巍, 等.基于F-P腔强度解调的微位移传感器[J].光学学报, 2014, 34(6):0628001_1-0628001_6. http://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201406043.htm LI C C, WANG M, XIA W, et al.A novel Fabry-Perot micro-displacement sensor based on intensity demodulation method[J].Acta Optica Sinica, 2014, 34(6):0628001_1-0628001_6(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201406043.htm
[4]	GANDER M J, MACPHERSON W N, BARTON J S, et al.Embedded micromachined fiber-optic Fabry-Perot pressure sensors in aerodynamics applications[J].IEEE Sensors Journal, 2003, 3(1):102-107. doi: 10.1109/JSEN.2003.810099
[5]	李坤, 文泓桥, 李慧.光纤法布里-珀罗结构的微型应变传感器的研制[J].光学学报, 2009, 9(12):3282-3285. http://www.cnki.com.cn/Article/CJFDTOTAL-GXXB200912008.htm LI K, WEN H Q, LI H.A study on miniature interferometer strain sensor based on EFPI[J].Acta Optica Sinica, 2009, 9(12):3282-3285(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-GXXB200912008.htm
[6]	SHAN N, SHI Y K, LIU X.Detecting crack of aircraft engine blade based on optical fiber F-P sensor[J].Nodestructive Testing, 2009, 31(3):206-207. http://en.cnki.com.cn/Article_en/CJFDTOTAL-WSJC200903013.htm
[7]	BHATIA V, MURPHY A, CLAUS R O, et al.Recent developments in optical-fiber-based extrinsic Fabry-Perot interferometric strain sensing technology[J].Smart Materials and Structures, 1995, 24(4):246-251.
[8]	YU Q X, ZHOU X L.Pressure sensor based on the fiber-optic extrinsic Fabry-Perot interferometer[J].Photonic Sensors, 2011, 1(1):72-83. doi: 10.1007/s13320-010-0017-9
[9]	MA C, DONG B, GONG J, et al.Decoding the spectra of low-finesse extrinsic optical fiber Fabry-Perot interferometers[J].Optics Express, 2011, 19(24):23723-23742. https://www.osapublishing.org/oe/abstract.cfm?uri=oe-19-24-23727#Abstract
[10]	MACPHERSON W N, KIDD S R, BARTON J S, et al.Phase demodulation in optical fiber Fabry-Perot sensors with inexact phase steps[J].IEEE Proc-Optoelectron, 1997, 144(3):130-133. doi: 10.1049/ip-opt:19971092
[11]	JIANG Y.Fourier transform white-light interferometry for the measurement of fiber-optic extrinsic Fabry-Perot interferometric sensors[J].IEEE Photonics Technology Letters, 2008, 20(2):75-77. doi: 10.1109/LPT.2007.912567
[12]	ZHANG X M, LIU Y, BAE H, et al.Phase demodulation with micromachined resonant mirrors for low-coherence fiber-tip pressure sensors[J].Optics Express, 2009, 17(26):23965-23974. doi: 10.1364/OE.17.023965
[13]	SCHMIDT M, FURSTENAU N.Fiber-optic extrinsic Fabry-Perot interferometer sensors with three-wavelength digital phase demodulation[J].Optics Letters, 1999, 24(9):599-601. doi: 10.1364/OL.24.000599
[14]	SCHMIDT M, WERTHER B, FURSTENAU N.Fiber-optic extrinsic Fabry-Perot interferometer strain sensors with < 50pm displacement resolution using three-wavelength digital phase demodulation[J].Optics Express, 2001, 8(8):475-480. doi: 10.1364/OE.8.000475
[15]	张佩. 基于光纤F-P传感器的动态解调算法的研究[D]. 武汉: 武汉理工大学, 2013. http://d.wanfangdata.com.cn/Thesis/Y2504382 ZHANG P.Study on methods of the dynamic demodulation for optical fiber Fabry-Perort sensors[D].Wuhan:Wuhan University of Technology, 2013(in Chinese). http://d.wanfangdata.com.cn/Thesis/Y2504382
[16]	SONG N F, CUI R Q, YANG Y J, et al.Fiber-optic extrinsic Fabry-Perot interferometer sensors with multi-wavelength intensity demodulation[C]//Mechanical Engineering, Materials Science and Civil Engineering Ⅱ.Zurich-Durnten:Trans Tech Publications Ltd., 2013:630-635.
[17]	MURPHY K, GUNTHER M, VENGSARKER A, et al.Quadrature phase-shifted extrinsic Fabry-Perot optical fiber sensors[J].Optics Letters, 1991, 16(4):273-275. doi: 10.1364/OL.16.000273
[18]	郁道银, 谈恒英.工程光学[M].2版.北京:机械工业出版社, 2011:310-313. YU D Y, TAN H Y.Engineering optics[M].2nd ed.Beijing:China Machine Press, 2011:310-313(in Chinese).