超临界层流翼型优化设计策略

邢宇; 罗东明; 余雄庆

doi:10.13700/j.bh.1001-5965.2016.0656

超临界层流翼型优化设计策略

doi: 10.13700/j.bh.1001-5965.2016.0656

南京航空航天大学飞行器先进设计技术国防重点学科实验室, 南京 210016

基金项目:

国家自然科学基金 11432007

详细信息

作者简介:
邢宇   男, 博士研究生。主要研究方向:飞行器多学科设计优化

罗东明   男, 博士, 讲师, 硕士生导师。主要研究方向:飞机总体设计、计算空气动力学

余雄庆   男, 博士, 教授, 博士生导师。主要研究方向:飞行器总体设计、飞行器多学科设计优化

通讯作者:
余雄庆, E-mail:yxq@nuaa.edu.cn

中图分类号: V221⁺.3
计量
- 文章访问数: 1014
- HTML全文浏览量: 217
- PDF下载量: 563
- 被引次数: 0
出版历程
- 收稿日期: 2016-08-09
- 录用日期: 2016-10-14
- 网络出版日期: 2017-08-20

Optimization strategy of supercritical laminar flow airfoil design

Key Laboratory of Fundamental Science for National Defense Advanced Design Technology of Flight Vehicle, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Funds:

National Natural Science Foundation of China 11432007

More Information

Corresponding author: YU Xiongqing, E-mail:yxq@nuaa.edu.cn

摘要

摘要:
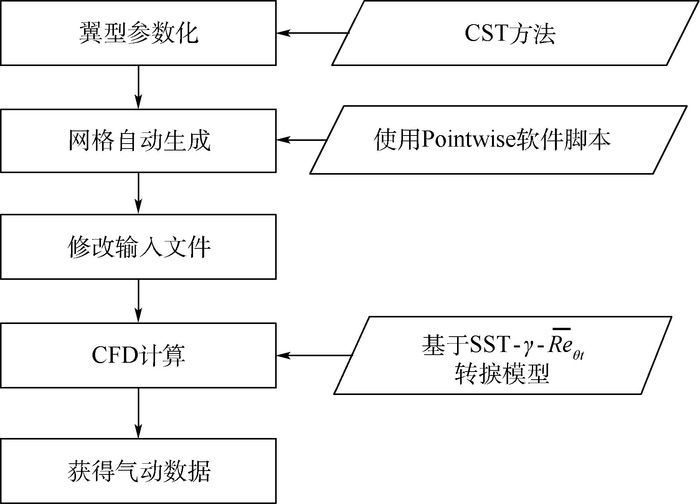
针对超临界层流翼型设计问题，提出一种两轮优化策略。采用γ-Re_θt转捩模型耦合剪切应力输运（SST）模式的湍流模型对翼型边界层转捩进行预测。翼型几何参数化建模采用形状分类函数转换（CST）方法，设计变量为描述翼型几何特征的参数。第1轮优化的目的是尽量提高层流区域的比例，气动分析模型为基于Kriging模型的代理模型，优化算法为遗传算法，通过优化获得满足约束要求的层流翼型。第2轮优化目的是对第1轮优化获得的翼型进行微调，进一步提高翼型的升阻比，气动分析直接采用CFD程序，优化算法采用基于梯度的优化算法。算例表明，应用本文提出的两轮优化策略，可将超临界翼型NASA SC（2）0412优化设计成超临界层流翼型，翼型的上下表面层流区比例分别达到了55.5%和47.0%，升阻比提高了38.1%。
- 层流 /
- 翼型 /
- 优化 /
- 空气动力学 /
- 代理模型
Abstract:
A two-step optimization strategy for the supercritical laminar flow airfoil design is proposed in the paper. The γ-Re_θt transition model coupled with the shear stress transportation (SST) turbulence model is used for prediction of airfoil boundary layer transition. The Class/Shape Transformation (CST) method is used to parameterize airfoil geometry. The parameters in the airfoil geometry model are used as the design variables. The first step of optimization is to increase the ratio of the laminar flow region. A genetic algorithm based on the Kriging surrogate model is employed to obtain the laminar flow airfoil with all constraints satisfied. The second step of optimization is to improve the optimization result of the first step, and to further increase the lift-to-drag ratio of the airfoil. A gradient based optimization is used to search optimal solution. The aerodynamic analysis during the second step optimization is implemented through the CFD code rather than the surrogate model. The example demonstrates that the supercritical airfoil NASA SC(2) 0412 can be optimized into a supercritical laminar flow airfoil by the two-step optimization method, the laminar region ratios on the airfoil upper and lower surface increase by 55.5% and 47.0% respectively, and the lift-to-drag ratio increases by 38.1%.
- laminar flow /
- airfoil /
- optimization /
- aerodynamics /
- surrogate model

HTML全文

图 1 转捩点位置计算与实验^[20]对比

Figure 1. Comparison of transition position between computation and experiment^[20]

下载: 全尺寸图片幻灯片

图 2 阻力系数计算与实验^[20]对比

Figure 2. Comparison of drag coefficient between computation and experiment^[20]

下载: 全尺寸图片幻灯片

图 3 超临界层流翼型优化设计流程

Figure 3. Optimization process of supercritical laminar flow airfoil design

下载: 全尺寸图片幻灯片

图 4 翼型NASA SC(2) 0412拟合的相对误差

Figure 4. Relative error for airfoil NASA SC(2) 0412 fitting

下载: 全尺寸图片幻灯片

图 5 气动分析流程

Figure 5. Process of aerodynamic analysis

下载: 全尺寸图片幻灯片

图 6 第1轮优化计算历程

Figure 6. Computational history of the first step of optimization

下载: 全尺寸图片幻灯片

图 7 初始翼型和第1轮优化后外形对比

Figure 7. Comparison of geometry between initial airfoil and the first step of optimization

下载: 全尺寸图片幻灯片

图 8 初始翼型和第1轮优化后压力系数分布对比

Figure 8. Comparison of pressure coefficient distribution between initial airfoil and the first step of optimization

下载: 全尺寸图片幻灯片

图 9 初始翼型和第1轮优化后摩擦阻力系数分布对比

Figure 9. Comparison of friction drag coefficient distribution between initial airfoil and the first step of optimization

下载: 全尺寸图片幻灯片

图 10 第2轮优化收敛历程

Figure 10. Convergence history of the second step of optimization

下载: 全尺寸图片幻灯片

图 11 第1轮和第2轮优化后翼型外形对比

Figure 11. Comparison of airfoil geometry between the first and second step of optimization

下载: 全尺寸图片幻灯片

图 12 第1轮和第2轮优化后压力系数分布对比

Figure 12. Comparison of pressure coefficient distribution between the first and second step of optimization

下载: 全尺寸图片幻灯片

图 13 第1轮和第2轮优化后摩擦阻力系数分布对比

Figure 13. Comparison of friction drag coefficient distribution between the first and second step of optimization

下载: 全尺寸图片幻灯片

表 1 设计变量

Table 1. Design variables

变量名	下限	初始值	上限
b₁	0.091 7	0.183 4	0.275 1
b₂	0.054 35	0.108 7	0.163 05
b₃	0.098 1	0.196 2	0.294 3
b₄	0.041 85	0.083 7	0.125 55
b₅	0.135 1	0.270 2	0.405 3
b₆	0.050 8	0.101 6	0.152 4
b₇	0.116 25	0.232 5	0.348 75
ζ_T1	0.001 65	0.003 3	0.004 95
b₈	-0.259 65	-0.173 1	-0.086 55
b₉	-0.214 8	-0.143 2	-0.071 6
b₁₀	-0.197 1	-0.131 4	-0.065 7
b₁₁	-0.279 45	-0.186 3	-0.093 15
b₁₂	-0.282 3	-0.188 2	-0.094 1
b₁₃	-0.117 6	-0.078 4	-0.039 2
b₁₄	0.105	0.21	0.315
ζ_T2	-0.003 3	-0.002 2	-0.001 1
α/(°)	0	0.3	0.6

下载: 导出CSV

参考文献(23)

[1]	SCHRAUF G.Status and perspectives of laminar flow[J].Aeronautical Journal, 2005, 109(1102):639-644. doi: 10.1017/S000192400000097X
[2]	THIBERT J J, RENEAUX J, SCHMITT V.Onera activities on drag reduction[C]//Proceedings of the 14th Congress of ICAS.Bonn:ICAS, 1990:1053-1064.
[3]	FUJINO M, YOSHIZAKI Y, KAWAMURA Y.Natural-laminar-flow airfoil development for a lightweight business jet[J].Journal of Aircraft, 2003, 40(4):609-615. doi: 10.2514/2.3145
[4]	FUJINO M.Design and development of the HondaJet[J].Journal of Aircraft, 2005, 42(3):755-764. doi: 10.2514/1.12268
[5]	BRADLEY M K, DRONEY C K.Subsonic ultra green aircraft research:Phase Ⅰ:Final report:NASA/CR-2011-216847[R].Washington, D.C.:NASA, 2011.
[6]	BRADLEY M K, DRONEY C K.Subsonic ultra green aircraft research phase Ⅱ:N+4 advanced concept development:NASA/CR-2012-217556[R].Washington, D.C.:NASA, 2012.
[7]	乔志德.自然层流超临界翼型的设计研究[J].实验流体力学, 1998(4):23-30. http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC804.003.htm QIAO Z D.Design of supercritical airfoils with natural laminar flow[J].Journal of Experiments in Fluid Mechanics, 1998(4):23-30(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC804.003.htm
[8]	杨青真, 张仲寅.超临界层流机翼边界层及气动特性分析[J].航空学报, 2004, 25(5):438-442. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB200405002.htm YANG Q Z, ZHANG Z Y.Analysis of the boundary layer and aerodynamic characteristics of a supercritical laminar wing[J].Acta Aeronautica et Astronautica Sinica, 2004, 25(5):438-442(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB200405002.htm
[9]	孙朋朋, 黄章峰.后掠角对后掠机翼边界层稳定性及转捩的影响[J].北京航空航天大学学报, 2015, 41(7):1313-1321. http://bhxb.buaa.edu.cn/CN/abstract/abstract13327.shtml SUN P P, HUANG Z F. Effect of sweep angle on stability and transition in swept-wing boundary layer[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7):1313-1321(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13327.shtml
[10]	靖振荣, 孙朋朋, 黄章峰.小攻角对后掠机翼边界层稳定性及转捩的影响[J].北京航空航天大学学报, 2015, 41(11):2177-2183. http://bhxb.buaa.edu.cn/CN/abstract/abstract13580.shtml JING Z R, SUN P P, HUANG Z F.Effect of attack angle on stability and transition in swept-wing boundary layer[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11):2177-2183(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13580.shtml
[11]	MENTER F R, LANGTRY R B, LIKKI S R, et al.A correlation-based transition model using local variables-Part Ⅰ:Model formulation[J].Journal of Turbomachinery, 2006, 128(3):413-422. doi: 10.1115/1.2184352
[12]	MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal, 1994, 32(8):1598-1605. doi: 10.2514/3.12149
[13]	LANGTRY R B.A correlation based transition model using local variables for unstructured parallelized CFD codes[R].Stuttgart:Stuttgart of University, 2006.
[14]	邓磊, 乔志德, 杨旭东, 等.高升阻比自然层流翼型多点/多目标优化设计[J].空气动力学学报, 2011, 29(3):330-335. http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201103010.htm DENG L, QIAO Z D, YANG X D, et al.Multi-point/objective optimization design of high lift-to-drag ratio for NLF airfoils[J].Acta Aerodynamica Sinica, 2011, 29(3):330-335(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201103010.htm
[15]	HAN Z H, CHEN J, ZHU Z, et al.Aerodynamic design of transonic natural-laminar-flow (NLF) wing via surrogate-based optimization:AIAA-2016-2041[R]. Reston:AIAA, 2016.
[16]	HAN Z H, DENG J, LIU J, et al.Design of laminar supercritical airfoils based on navier-stokes equations[C]//Proceedings of 28th International Congress of the Aeronautical Sciences. Bonn:ICAS, 2012:1-9.
[17]	ZHAO K, GAO Z H, HUANG J T.Robust design of natural laminar flow supercritical airfoil by multi-objective evolution method[J].Applied Mathematics and Mechanics, 2014, 35(2):191-202. doi: 10.1007/s10483-014-1783-6
[18]	ZHANG Y F, FANG X M, CHEN H X, et al.Supercritical natural laminar flow airfoil optimization for regional aircraft wing design[J].Aerospace Science and Technology, 2015, 43:152-164. doi: 10.1016/j.ast.2015.02.024
[19]	马晓永, 张彦军, 段卓毅, 等.自然层流机翼气动外形优化研究[J].空气动力学学报, 2015, 33(6):812-817. http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201506016.htm MA X Y, ZHANG Y J, DUAN Z Y, et al.Study of aerodynamic shape optimization for natural laminar wing[J].Acta Aerodynamica Sinica, 2015, 33(6):812-817(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201506016.htm
[20]	BARCHE J, BINJON T W, WINTER K G, et al. Experimental data base for computer program assessment:AGARDAR-138[R].London:Technical Editing and Reproduction Ltd., 1979:1-22.
[21]	郑宇宁, 邱志平, 黄仁, 等.二元可变后缘翼型的鲁棒优化设计[J].北京航空航天大学学报, 2015, 41(5):897-903. http://bhxb.buaa.edu.cn/CN/abstract/abstract13252.shtml ZHENG Y N, QIU Z P, HUANG R, et al.Robust design optimization of a two-dimensional airfoil with deformable trailing edge[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5):897-903(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13252.shtml
[22]	BOGUE D, CRIST N.CST transonic optimization using tran-air++:AIAA-2008-321[R].Reston:AIAA, 2008.
[23]	赵童, 张宇飞, 陈海昕, 等.面向三维机翼性能的超临界翼型优化设计方法[J].中国科学:物理学力学天文学, 2015, 45(10):104708. http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201510009.htm ZHAO T, ZHANG Y F, CHEN H X, et al.Aerodynamic optimization method of supercritical airfoil geared to the performance of swept and tapered wing[J].Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(10):104708(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201510009.htm