基于多模型的不等长序列数据关联算法

孙贵东; 关欣; 衣晓; 赵骏

doi:10.13700/j.bh.1001-5965.2016.0658

基于多模型的不等长序列数据关联算法

doi: 10.13700/j.bh.1001-5965.2016.0658

孙贵东¹,
关欣^1, ,,
衣晓¹,
赵骏²

1.
海军航空工程学院电子信息工程系, 烟台 264001
2.
91934 部队, 义乌 322000

基金项目:

国家自然科学基金 61032001

新世纪优秀人才支持计划 NCET-11-0872

详细信息

作者简介:
孙贵东   男, 博士研究生。主要研究方向:智能数据挖掘、多属性决策

关欣   女, 博士, 教授, 博士生导师。主要研究方向:多源信息融合、智能信息处理

衣晓   男, 博士, 教授, 博士生导师。主要研究方向:无线传感器网络、多源信息融合

通讯作者:
关欣, E-mail:gxtongwin@163.com

中图分类号: TN95
计量
- 文章访问数: 917
- HTML全文浏览量: 149
- PDF下载量: 403
- 被引次数: 0
出版历程
- 收稿日期: 2016-08-10
- 录用日期: 2016-10-28
- 网络出版日期: 2017-08-20

Data association algorithm for unequal length sequence based on multiple model

SUN Guidong¹,
GUAN Xin^{1
, ,},
YI Xiao¹,
ZHAO Jun²

1.
Department of Electronics and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China
2.
91934 Army, Yiwu 322000, China

Funds:

National Natural Science Foundation of China 61032001

Program for New Century Excellent Talents in University NCET-11-0872

More Information

Corresponding author: GUAN Xin, E-mail:gxtongwin@163.com

摘要

摘要:
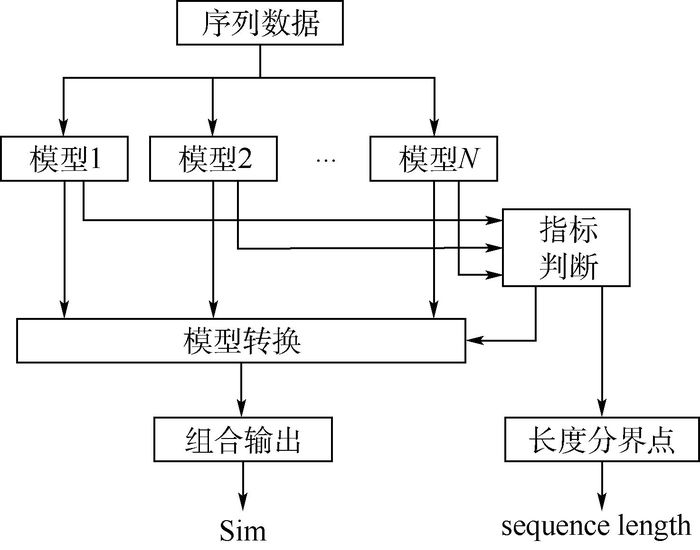
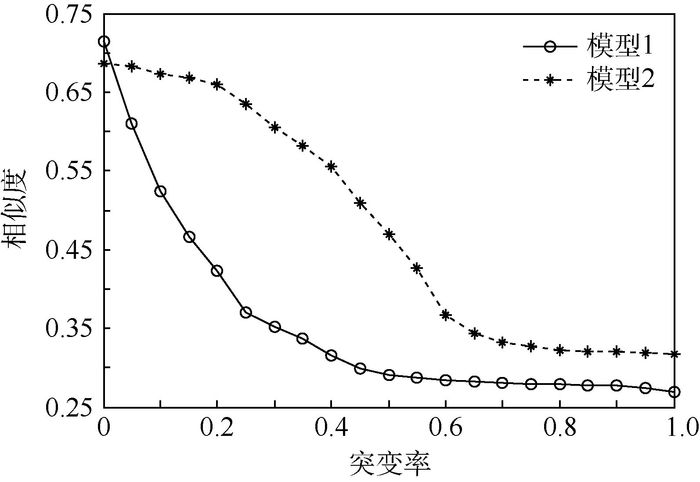
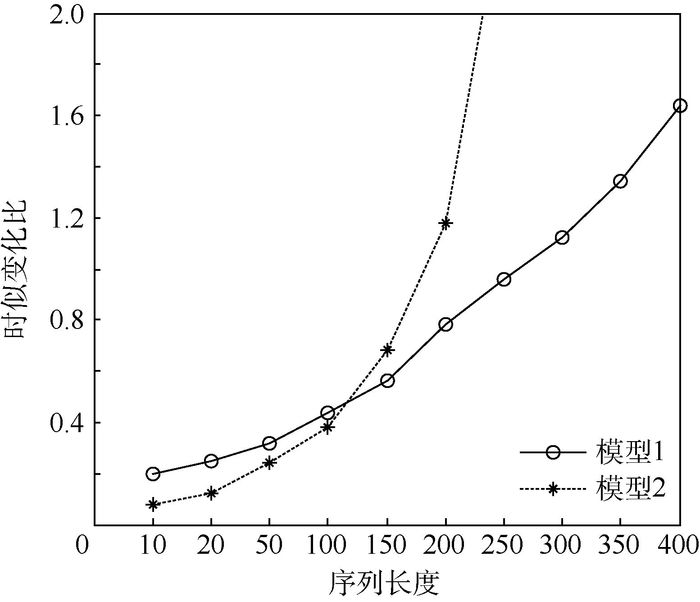
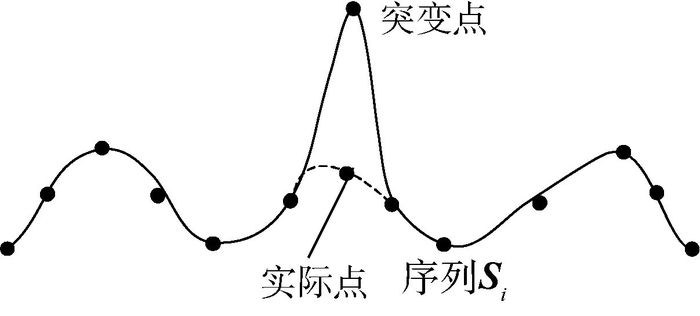
单模型在处理不等长序列数据关联时不能兼顾计算精度、复杂度和抗扰性，为此提出了基于多模型（MM）的不等长序列数据关联算法。将基于滑动窗口和动态时间弯曲（DTW）的不等长序列相似度度量模型作为MM的输入模型，以2种模型计算得到的时似变化比作为模型判断指标进行模型转换，实现了2种模型的优势互补，并得到模型的应用条件，最后输出MM作用后的不等长序列相似度，以此作为关联指标进行关联判定。仿真实验验证了MM关联算法在处理不等长序列数据关联的有效性，并对序列长度和突变率变化对关联效果的影响进行了分析。
- 数据关联 /
- 不等长度 /
- 序列相似度 /
- 多模型(MM) /
- 时似变化比
Abstract:
When dealing with data association for unequal length sequence, single model cannot balance computational accuracy, complexity and disturbance rejection. So a data association algorithm for unequal length sequence based on multiple model (MM) was proposed. The two unequal length sequence similarity measurement model based on sliding window and dynamic time warping (DTW) were selected as the input model of MM, which uses the rate of change between time and similarity of two model as the index to realize the transformation of the two models. It combines both advantages of two models and gets the models' application condition.The unequal length sequence similarity is output after MM as the index to judge the association of the sequence data. Simulation results show the effectiveness of the proposed algorithm for unequal length sequence and analyze the effect of sequence length and fluctuant rate on association result.
- data association /
- unequal length /
- sequence similarity /
- multiple model (MM) /
- rate of change between time and similarity

HTML全文

图 1 突变点示意图

Figure 1. Schematic diagram of fluctuant point

下载: 全尺寸图片幻灯片

图 2 模型转换流程图

Figure 2. Model transformation flowchart

下载: 全尺寸图片幻灯片

图 3 2种模型计算时间对比

Figure 3. Comparison of calculation time between two models

下载: 全尺寸图片幻灯片

图 4 模型相似度随序列长度变化

Figure 4. Variation of model similarity with sequence length

下载: 全尺寸图片幻灯片

图 5 模型相似度随突变率变化

Figure 5. Variation of model similarity with fluctuant rate

下载: 全尺寸图片幻灯片

图 6 时似变化比随序列长度的变化

Figure 6. Variation of rate of change between time and similarity with sequence length

下载: 全尺寸图片幻灯片

图 7 不同突变点条件下的模型转换临界点变换

Figure 7. Change of model transformation critical point under different fluctuant points

下载: 全尺寸图片幻灯片

表 1 不等长序列组的相似度

Table 1. Similarity of unequal length sequence group

序列相似度

Q¹ Q² Q³ Q⁴

S¹ 0.212 5 0.696 6 0.105 6 0.010 2
S² 0.126 4 0.075 9 0.730 6 0.078 7

下载: 导出CSV

参考文献(16)

[1]	AGRAWAL R, FALOUTSOS C, SWAMI A.Efficient similarity search in sequence databases[C]//Proceedings of 4th International Conference on Foundations of Data Organization and Algorithms.Berlin:Springer, 1993:69-84.
[2]	RAFIEI D, MENDELZON A O.Querying time series data based on similarity[J].IEEE Transactions on Knowledge and Data Engineering, 2000, 12(5):675-693. doi: 10.1109/69.877502
[3]	WANG C Z, WANG X Y.Multilevel filtering for high dimensional nearest neighbor search[C]//Proceedings of ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery.New York:ACM Press, 2000:37-43.
[4]	KORN F, JAGADISH H V, FALOUTSOS C.Efficiently supporting ad hoc queries in large datasets of time sequences[C]//Proceedings of ACM SIGMOD International Conference on Management of Data.New York:ACM Press, 1997:289-300.
[5]	HUHTALLA Y, KRKKINEN J, TOIVENEN H.Mining for similarities in aligned time series using wavelets[C]//Proceedings of Data Mining and Knowledge Discovery:Theory, Tools, and Technology.Orlando:[s.n.], 1999:150-160.
[6]	张海勤, 蔡庆生.基于小波变换的时间序列相似模式匹配[J].计算机学报, 2003, 26(3):373-377. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200303015.htm ZHANG H Q, CAI Q S.Time series similarity querying based on wavelets[J].Computer Journal, 2003, 26(3):373-377(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200303015.htm
[7]	KEOGH E.Data mining and machine learning in time series database[C]//Proceedings of the 5th Industrial Conference on Data Mining (ICDM).Leipzig:[s.n.], 2005.
[8]	KEOGH E, CHAKRABARTI K, PAZZANI M, et al.Dimensionality reduction for fast similarity search in large time series databases[J].Journal of Knowledge and Information Systems, 2001, 3(3):263-286. doi: 10.1007/PL00011669
[9]	SANG W K, SANGH Y P, WEALEY W C.An Index-based approach for similarity search supporting time warping in large sequence databases[C]//Proceedings 17th International Conference on Data Engineering.Washington, D.C.:IEEE Computer Society, 2001:607-614.
[10]	THANNWIN R, BILSON C, KEOGH E.Searching and mining trillions of time series subsequences under dynamic time warping[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM Press, 2012:262-270.
[11]	KEOGH E.Exact indexing of dynamic time warping[C]//Proceedings of the 28th International Conference on Very Large Databases.San Francisco:Morgan Kaufmann, 2002:406-417.
[12]	RATHT M, MANMATHA R.Lower bounding of dynamic time warping distances for multivariate time series:Technical ReportMM-40[R].Amherst:Center for Intelligent Information Retrieval Technical Report, University of Massachusetts, 2003.
[13]	KEOGT E, PAZZANI M.Derivative dynamic time warping[C]//Proceedings of the 1st SIAM International Conference on Data Mining.Chicago:SIAM Press, 2001:209-211.
[14]	KEOGH E, CHAKRABARTI K, PAZZANI M.Locally adaptive dimensionality reduction for indexing large time series databases[J].ACM Transactions on Database Systems, 2002, 27(2):188-228. doi: 10.1145/568518.568520
[15]	BERNDT D, CLIFFORD J.Using dynamic time warping to find patterns in time series[C]//AIAA 94 Workshop on Knowledge Discovery in Databases.Reston:AIAA, 1994:359-370.
[16]	BAR-SHALOM Y, FORTMANN T E.Tracking and data association[M].San Diego:Academic Press, 1988:125-127.