蜻蜓爬升过程间歇性拍动飞行现象的数值研究

刘佳佳; 郑孟宗; 潘天宇; 李秋实

doi:10.13700/j.bh.1001-5965.2016.0766

蜻蜓爬升过程间歇性拍动飞行现象的数值研究

doi: 10.13700/j.bh.1001-5965.2016.0766

北京航空航天大学能源与动力工程学院, 北京 100083

基金项目:

北京航空航天大学研究生创新实践基金 YCSJ-01-2016-06

详细信息

作者简介:
刘佳佳女, 硕士研究生。主要研究方向:非定常气体动力学

潘天宇男, 博士。主要研究方向:流动稳定性

通讯作者:
潘天宇, E-mail: pantianyu@buaa.edu.cn

中图分类号: V211.7
计量
- 文章访问数: 818
- HTML全文浏览量: 111
- PDF下载量: 299
- 被引次数: 0
出版历程
- 收稿日期: 2016-09-29
- 录用日期: 2016-12-16
- 网络出版日期: 2017-10-20

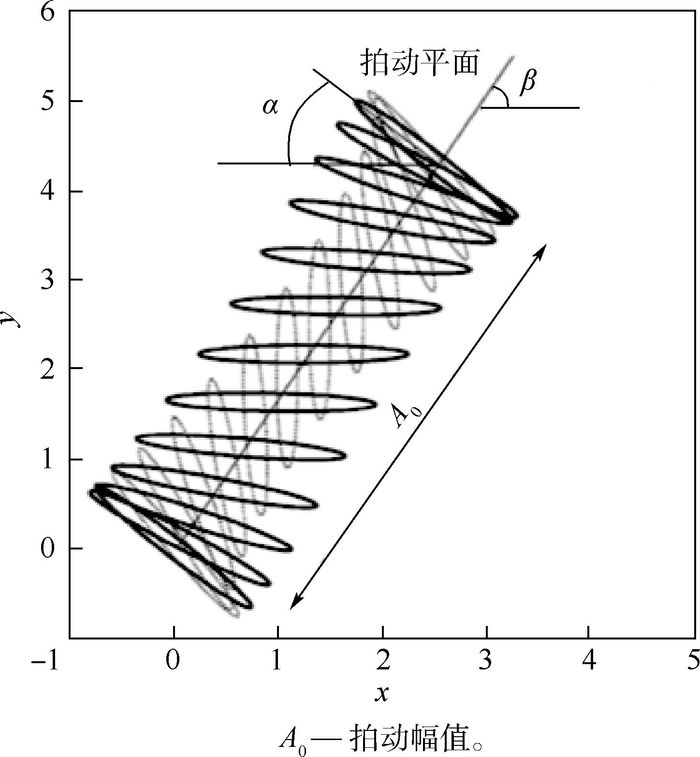
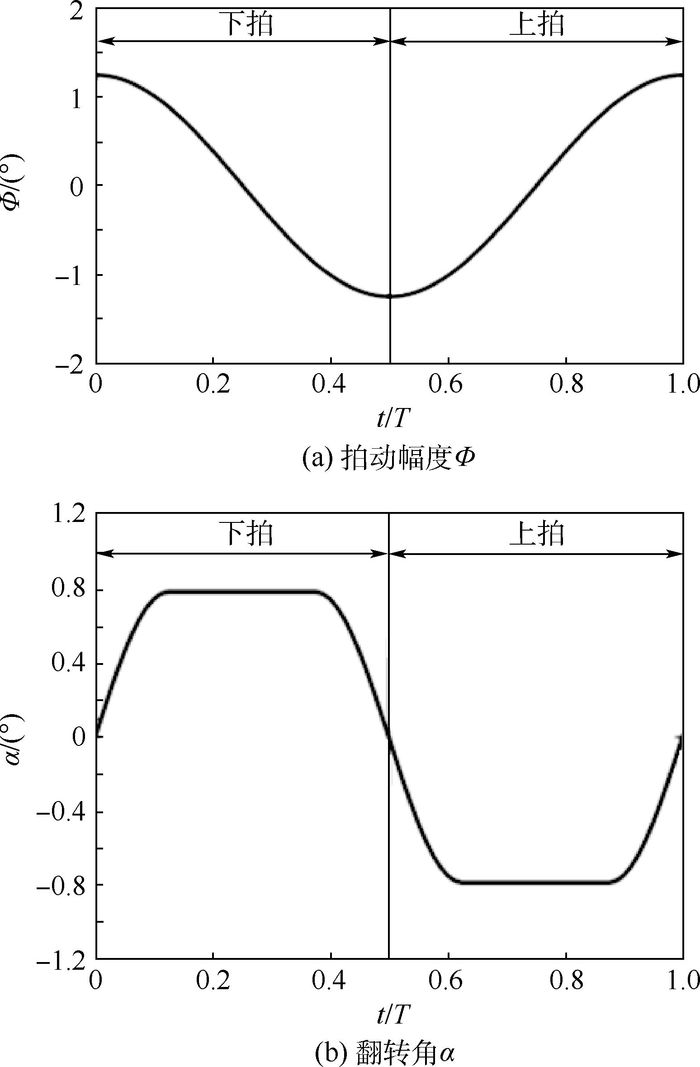
Numerical study on intermittent flapping flight performance of dragonfly during climbing

School of Energy and Power Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

Funds:

Innovation and Practice Fund for Graduate Student of Beihang YCSJ-01-2016-06

More Information

Corresponding author: PAN Tianyu, E-mail: pantianyu@buaa.edu.cn

摘要

摘要:
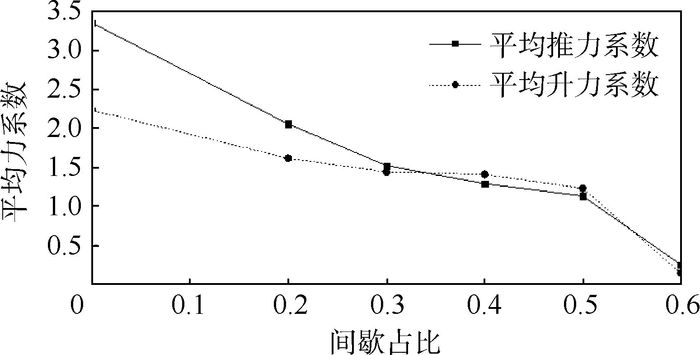
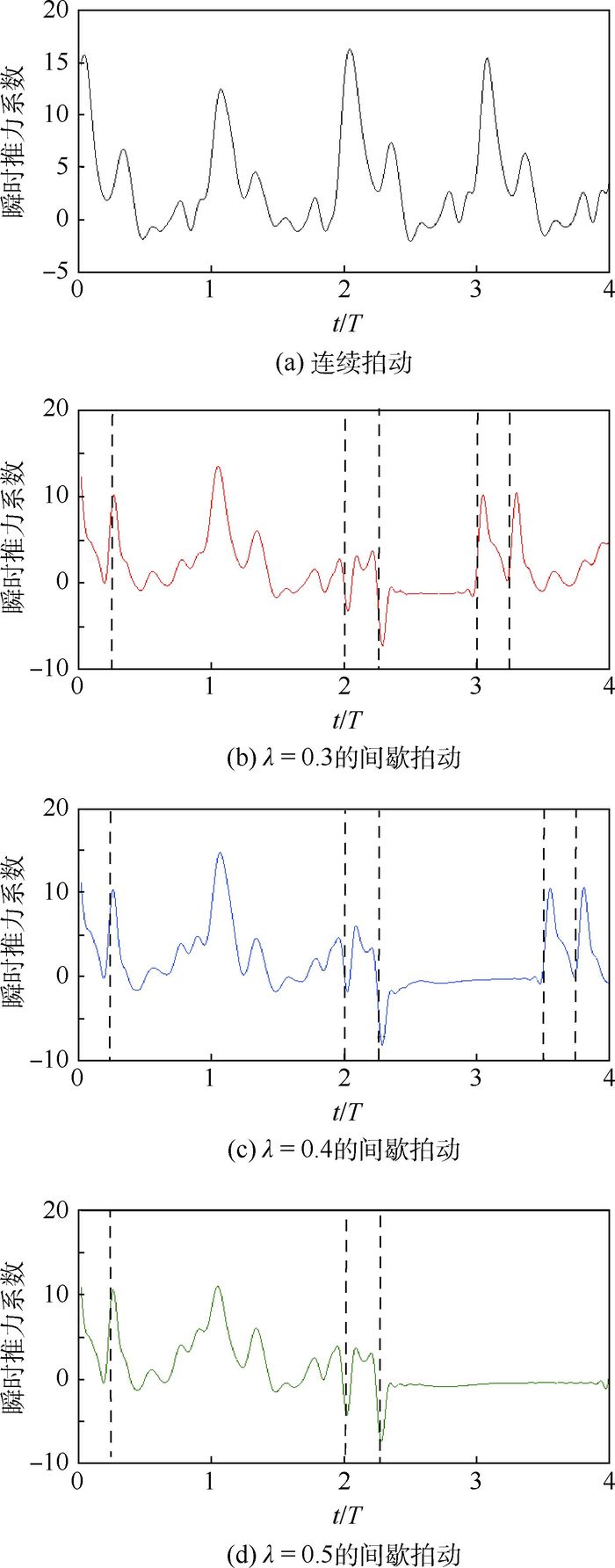
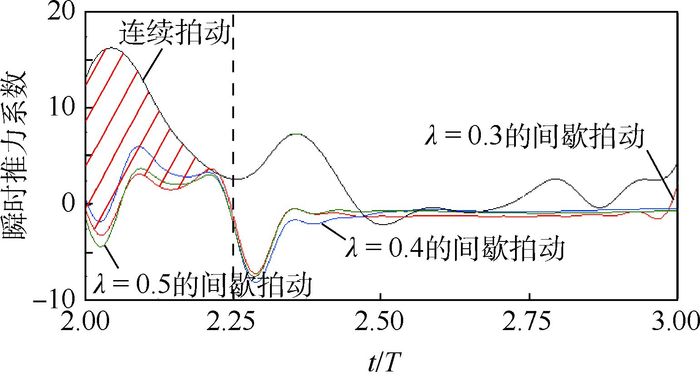
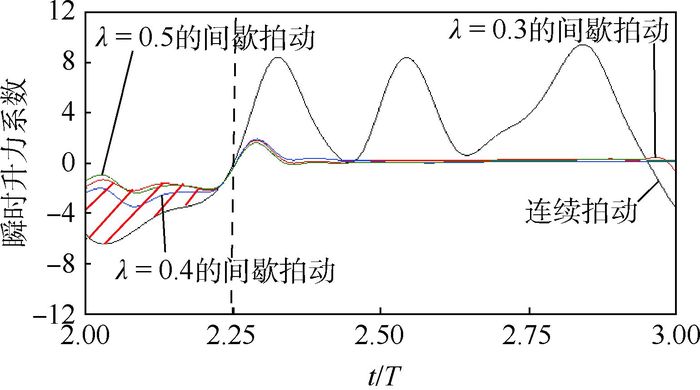
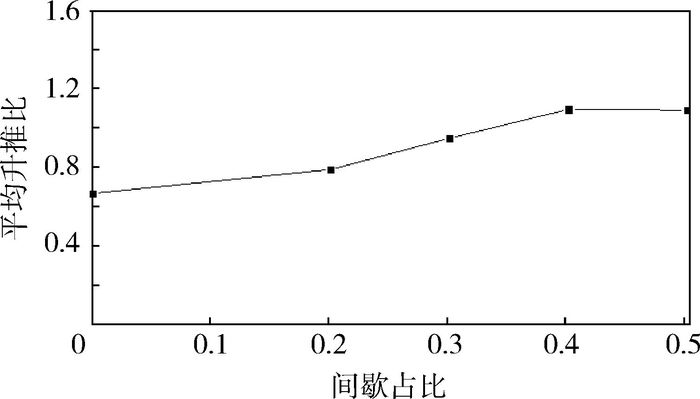
采用数值模拟方法研究了蜻蜓双翼做间歇性拍动运动时的气动特征。计算结果表明，在所研究的雷诺数工况下（Re=157），模型翼的平均升力系数和平均推力系数随着间歇占比的增大而减小，前段下降较快，中段下降平缓，后段下降至零。其中平均推力系数受到的影响相对平均升力系数更大，当连续飞行转变为间歇性飞行时，短暂滑翔初期和短暂滑翔稳定阶段均大幅削弱推力系数，共占42.7%；而对于升力系数，短暂滑翔稳定期对升力系数的削弱作用很大，占41.4%，但短暂滑翔初期却对平均升力系数的提高贡献8%。间歇拍动飞行能够提高蜻蜓飞行的升推比，当滑翔时长占间歇飞行周期之比为0.3时，平均升推比接近为1。
- 蜻蜓 /
- 间歇性拍动 /
- 异步拍动 /
- 推力系数 /
- 升力系数
Abstract:
Aerodynamic force generation in a dragonfly intermittent flapping flight with modeled wings was studied using the method of numerical simulation. The computational results show that the average lift coefficient and average thrust coefficient of the modeled wing decrease with the increase of the intermittent proportion at the Reynolds number of 157. They descend faster in the frontal part, while gently in the middle part, and decrease to zero in the latter part. The average thrust coefficient is affected greater than the average lift coefficient. When the continuous flight turns into intermittent flight, the thrust coefficient during the early phase and stable phase of short gliding is significantly weakened with totally 42.7%; For the lift coefficient, it is mainly weakened during the stable phase of short gliding, accounting for 41.4%, but the early phase of short gliding has a contribution of 8% to the increase of average lift coefficient. Intermittent flapping flight is possible to improve the lift-thrust ratio in dragonfly flight. When the the proportion of gliding time to intermittent flight cycle is 0.3, the average lift-thrust ratio is close to 1.
- dragonfly /
- intermittent flapping /
- asynchronous flapping /
- thrust coefficient /
- lift coefficient

HTML全文

图 1 圆柱在计算域中的相对位置

Figure 1. Relative position of circular cylinder in computational domain

下载: 全尺寸图片幻灯片

图 2 圆柱绕流阻力系数对比

Figure 2. Comparison of drag coefficient of flow around a circular cylinder

下载: 全尺寸图片幻灯片

图 3 单翼在一个周期内的扑翼规律

Figure 3. Wing flapping law of single wing in a stroke

下载: 全尺寸图片幻灯片

图 4 φ为0°时拍动幅度Φ和翻转角α在一个周期内随时间变化运动函数

Figure 4. Time-dependent motion function of flapping amplitude Φ and pitching angle α in a stroke (φ=0°)

下载: 全尺寸图片幻灯片

图 5 蜻蜓爬升过程中翼面拍动幅度随时间变化曲线

Figure 5. Time-dependent flapping amplitude of dragonfly wings during climbing

下载: 全尺寸图片幻灯片

图 6 平均力系数随间歇占比的变化

Figure 6. Variation of average force coefficient with different gliding time proportions

下载: 全尺寸图片幻灯片

图 7 不同间歇占比的间歇拍动飞行的瞬时推力系数

Figure 7. Time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight

下载: 全尺寸图片幻灯片

图 8 不同间歇占比的间歇拍动飞行的瞬时推力系数在t/T∈(0, 1) 期间的变化规律对比

Figure 8. Comparison of change laws of time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(0, 1)

下载: 全尺寸图片幻灯片

图 9 不同间歇占比的间歇拍动飞行的瞬时推力系数在t/T∈(2, 3) 期间的变化规律对比

Figure 9. Comparison of change laws of time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(2, 3)

下载: 全尺寸图片幻灯片

图 10 不同间歇占比的间歇拍动飞行的瞬时升力系数

Figure 10. Time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight

下载: 全尺寸图片幻灯片

图 11 不同间歇占比的间歇拍动飞行的瞬时升力系数在t/T∈(0, 1) 期间的变化规律对比

Figure 11. Comparison of change laws of time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(0, 1)

下载: 全尺寸图片幻灯片

图 12 不同间歇占比的间歇拍动飞行的瞬时升力系数在t/T∈(2, 3) 期间的变化规律对比

Figure 12. Comparison of change laws of time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(2, 3)

下载: 全尺寸图片幻灯片

图 13 平均升推比随间歇占比的变化

Figure 13. Variation of average lift-thrust ratio with different gliding time proportions

下载: 全尺寸图片幻灯片

表 1 Re=25圆柱绕流流场细节对比

Table 1. Comparison of flow field details around a circular cylinder at Re=25

结果来源	尾迹长度	尾迹最宽处 x轴坐标	尾涡中心 x轴坐标	两尾涡中心点的 y方向距离
本文	1.20	0.89	1.04	0.42
Gresho^[15]	1.15	0.81	0.88	0.47
Saiki^[16]	1.41		1.03	0.50
Coutanceau^[17]	1.22	0.85	0.94	0.51

下载: 导出CSV

参考文献(22)

[1]	SUN M.Insect flight dynamics:Stability and control[J].Reviews of Modern Physics, 2014, 86(2):615-646. doi: 10.1103/RevModPhys.86.615
[2]	WEIS-FOGH T.Quick estimates of flight fitness in hovering an-imals, including novelmechanism for lift production[J].Journal of Experimental Biology, 1973, 59(1):169-230.
[3]	ELLINGTON C P, VAN DEN BERG C, WILLMOTT A P.Leading edge vortices in insect flight[J].Nature, 1996, 384(6610):626-630. doi: 10.1038/384626a0
[4]	DICKINSON M H, LEHMANN F O, SANE S P.Wing rotation and the aerodynamic basis of insect flight[J].Science, 1999, 284(5422):1954-1960. doi: 10.1126/science.284.5422.1954
[5]	SUN M, TANG J.Unsteady aerodynamic force generation by a model fruit flywing in flappingmotion[J].Journal of Experimental Biology, 2002, 205(1):55-70. http://www.ncbi.nlm.nih.gov/pubmed/11818412
[6]	AZUMA A, WATANABE T.Flight performance of a dragonfly[J].Journal of Experimental Biology, 1988, 137(1):221-252.
[7]	WAKELING J M, ELLINGTON C P.Dragonfly flight.Ⅱ.Velocities, accelerations and kinematics of flapping flight[J].Journal of Experimental Biology, 1997, 200(3):557-582. https://www.ncbi.nlm.nih.gov/pubmed/9318255
[8]	WAKELING J M, ELLINGTON C P.Dragonfly flight.I.Gliding flight and steady-state aerodynamic forces[J].Journal of Experimental Biology, 1997, 200(3):543-556. http://www.ncbi.nlm.nih.gov/pubmed/9318238
[9]	WAKELING J, ELLINGTON C.Dragonfly flight.Ⅲ.Lift and power requirements[J].Journal of Experimental Biology, 1997, 200(3):583-600. https://www.mendeley.com/research-papers/dragonfly-3-lift-power-requirements/
[10]	WANG Z J, RUSSELL D.Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight[J].Physical Review Letters, 2007, 99(14):12243-12254. https://www.ncbi.nlm.nih.gov/pubmed/17930724
[11]	DONG H, KOEHLER C, LIANG Z, et al.An integrated analysis of a dragonfly in free flight:AIAA-2010-4390[R].Reston:AIAA, 2010.
[12]	高倩, 郑孟宗, 李志平, 等.蜻蜓爬升过程飞行特征实验研究[J].北京航空航天大学学报, 2016, 42(6):1271-1278. http://bhxb.buaa.edu.cn/CN/abstract/abstract13982.shtml GAO Q, ZHENG M Z, LI Z P, et al.Experimental study on flight performance of dragonfly during climbing[J].Journal of Beijing University of Aeronautics and Astronsutics, 2016, 42(6):1271-1278(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13982.shtml
[13]	FADLUN E A, VERZICCO R, ORLANDI P, et al.Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations[J].Journal of Computational Physics, 2000, 161(1):35-60. doi: 10.1006/jcph.2000.6484
[14]	MOHD-YUSOF J.Combined immersed-boundary/B-spline methods for simulations of flow in complex geometries[C]//Annual Research Briefs, 1997:317-327.
[15]	GRESHO P M, CHAN S T, LEE R L, et al.A modified finite element method for solving the time-dependent, incompressible Navier-Stokes equations.Part 2:Applications[J].International Journal for Numerical Methods in Fluids, 1984, 4(7):619-640. doi: 10.1002/(ISSN)1097-0363
[16]	SAIKI E M, BIRINGEN S.Numerical simulation of a cylinder in uniform flow:Application of a virtual boundary method[J].Journal of Computational Physics, 1996, 123(2):450-465. doi: 10.1006/jcph.1996.0036
[17]	COUTANCEAU M, BOUARD R.Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation.Part 2.Unsteady flow[J].Journal of Fluid Mechanics, 1977, 79(2):257-272. doi: 10.1017/S0022112077000147
[18]	SILVA L E, SILVEIRA-NETO A, DAMASCENO J J R.Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method[J].Journal of Computational Physics, 2003, 189(2):351-370. doi: 10.1016/S0021-9991(03)00214-6
[19]	PARK J, KWON K, CHOI H.Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J].KSME International Journal, 1998, 12(6):1200-1205. doi: 10.1007/BF02942594
[20]	WIESELSBERGER C.New data on the laws of fluid resistance[J].Physikalische Zeitschrift, 1921, 22:321-328.
[21]	RELF E F.An electrical method for tracing stream lines in the two-dimensional motion of a perfect fluid[J].Philosophical Magazine, 1924, 29(285):535-539.
[22]	JANE W Z.Two dimensional mechanism for insect hovering[J].Physical Review Letters, 2000, 85(10):2216-2219. doi: 10.1103/PhysRevLett.85.2216