-
摘要:
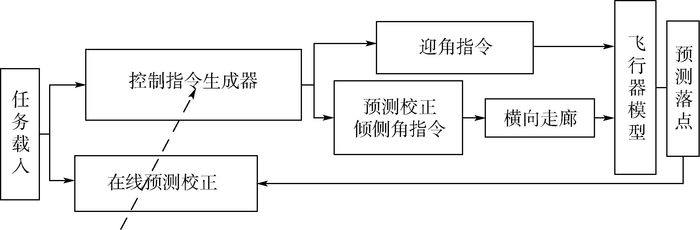
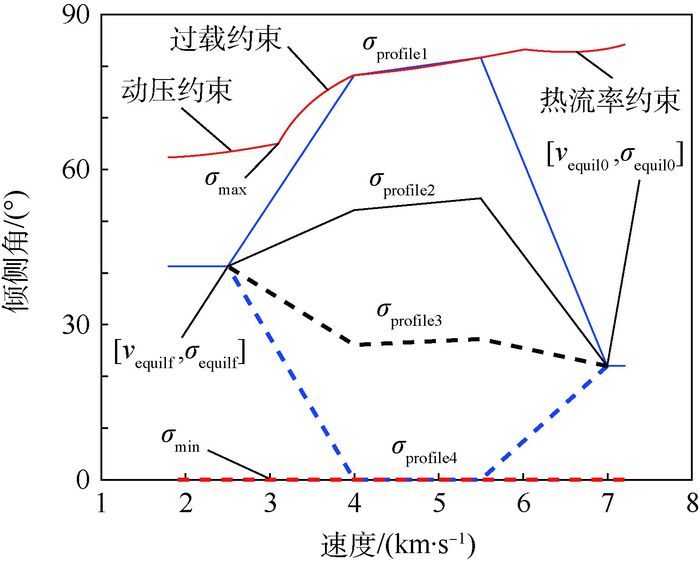
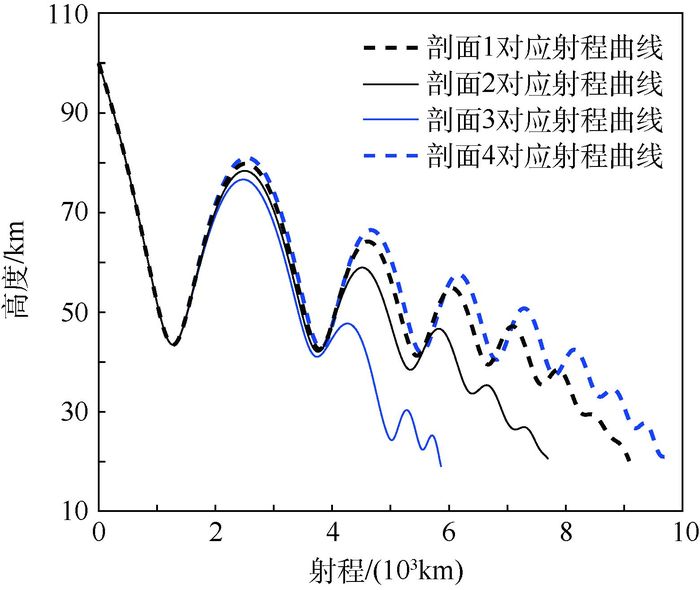
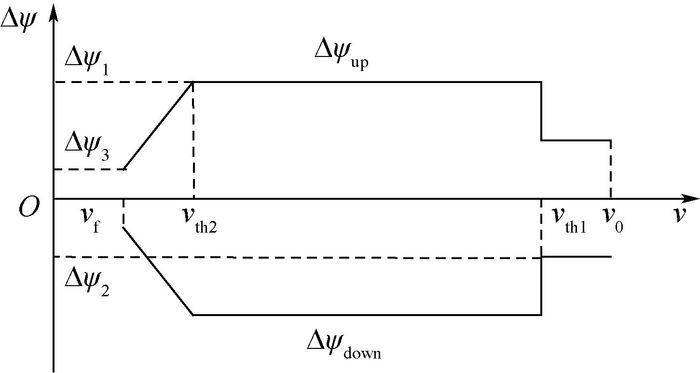
针对传统预测校正算法在再入过程中弹道性能与约束无法保障等问题，提出了一种基于倾侧角参数化的离线弹道优化与在线预测校正相结合的再入制导方法。基于平衡滑翔条件对过程约束进行分析，并证明了倾侧角剖面对射程的单调性。离线部分通过控制量参数化（CVP）方法构建控制模型，并使用序列二次规划（SQP）方法对弹道进行优化，从而大幅度提高弹道性能。在线部分利用Gauss-Newton法实时对弹道进行迭代求解，得出满足终端约束的倾侧角剖面，引导飞行器平稳、精确地飞向末端能量段并满足射程约束，Gauss-Newton法求解弹道具有收敛速度快、精度高的特点。针对高升阻比飞行器导致平衡滑翔条件难以成立以及飞行过程中的强干扰使约束超出的问题，提出了一种约束限制方法，对再入时的过程约束进行了有效的保障。仿真结果表明，本文方法对投放偏差、飞行器参数与大气模型等不确定因素具有良好的鲁棒性，对弹道性能的保障具有工程应用价值。
Abstract:In view of current research situation that the ballistic performance and constraints are unable to be guaranteed by traditional prediction correction algorithm in the reentry process, a new reentry guidance method was proposed, which combines the offline trajectory optimization based on simple parameterization of bank angle profile and the online prediction and correction. Process constraints were analyzed through equilibrium glide condition and the monotonic property of range to bank angle profile was proved. For offline section, control model was built through control variable parameterization (CVP) and the trajectory was optimized through sequence quadratic program (SQP) to improve the ballistic performance greatly. For online section, the solution of bank angle profile was obtained in real time, which satisfied terminal constraints through trajectory iteration based on Gauss-Newton method. Gauss-Newton method has fast convergence speed and high precision for solving trajectory. Finally, a constraint limit method was proposed to cope with the problems that high L/D aircraft would make equilibrium glide condition hard to be established and that strong interference would make constraints be violated, which provided powerful protection to process constraints in reentry. The simulation results show that this method is adaptable to uncertain factors such as throwing deviation, aircraft parameters and atmospheric model, and is of engineering application value for trajectory performance guarantee.
-
表 1 仿真条件
Table 1. Simulation conditions
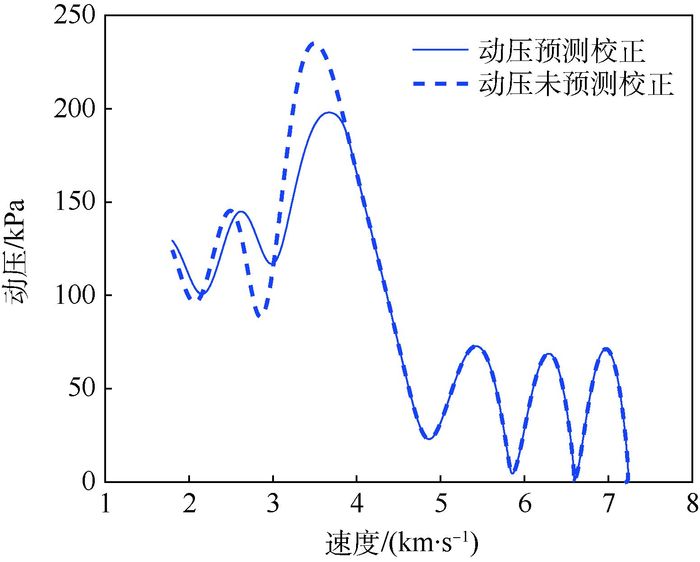
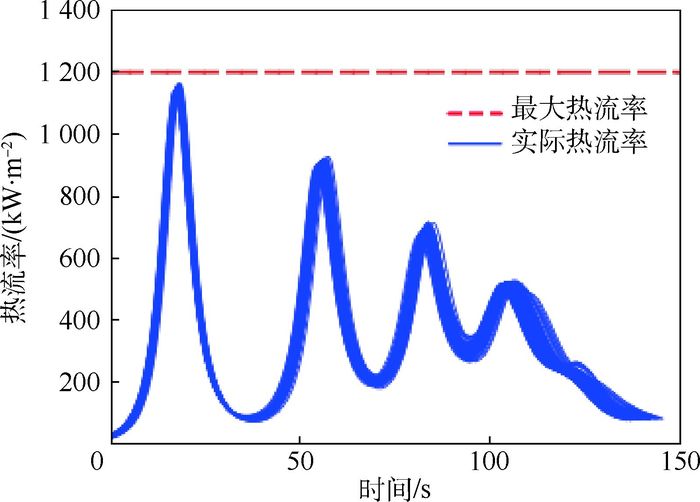
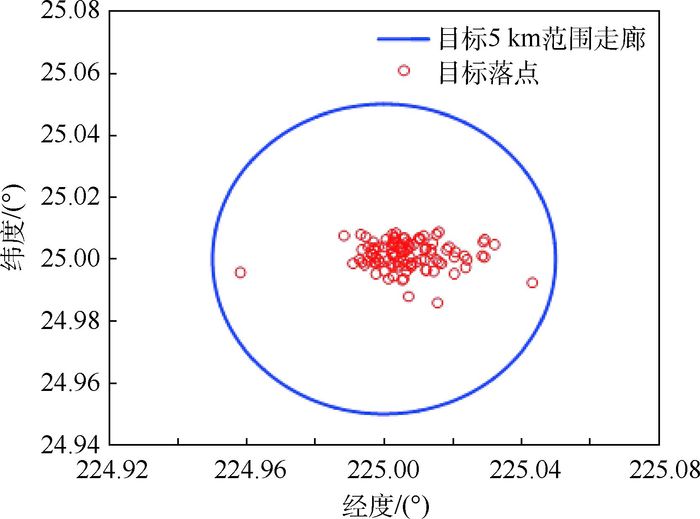
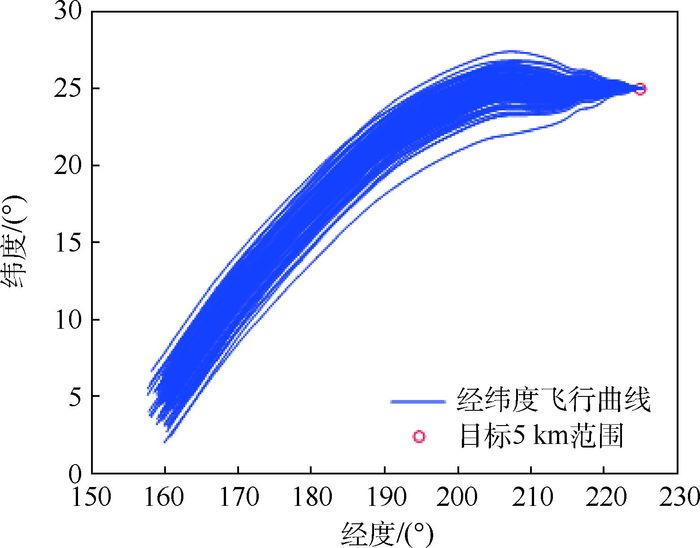
参数 数值 初始点 高度/km 100 经度/(°) 160 纬度/(°) 5 速度/(m·s-1) 7 200 速度倾斜角/(°) -2 速度航向角/(°) 55 终端约束 高度/km 20 速度/(m·s-1) 1 800 目标经度/(°) 225 目标纬度/(°) 25 过程约束 热流率/(kW·m-2) ≤1 200 动压/kPa ≤200 过载/g0 ≤4 
下载: 导出CSV
表 2 弹道求解精度
Table 2. Accuracy of trajectory solvingkm
km 剩余射程Sgo 求解弹道射程Spre 射程偏差Sgo-Spre 6 210.562 72 6 210.564 78 -0.002 1 6 500.000 00 6 499.967 92 0.032 1 7 000.000 00 6 999.997 80 0.002 2 7 500.000 00 7 499.971 33 0.028 7 8 000.000 00 7 999.998 06 0.001 9 8 462.523 64 8 462.519 51 0.004 1
下载: 导出CSV
表 3 弹道求解时间
Table 3. Time of trajectory solving
参数 次数 最大
时间/s最小
时间/s平均
时间/s时间
标准差/s数值 27 0.796 4 0.096 1 0.477 1 0.227 1
下载: 导出CSV
表 4 总气动热对比
Table 4. Comparison of total aerodynamic heat
射程/km 离线气动热/kJ 在线气动热/kJ 偏差/% 5 775.8 419 771 422 666 0.69 6 267.9 439 710 442 212 0.57 6 764.7 459 646 462 756 0.68 7 264.8 476 898 480 360 0.73 7 767.2 493 759 496 492 0.55 8 270.9 505 929 509 214 0.65 8 775.2 524 966 528 531 0.68 9 279.5 545 929 550 088 0.76 9 782.9 560 820 566 370 0.99
下载: 导出CSV
表 5 参数拉偏表
Table 5. Parameter deviation table
参数 拉偏值 高度/km 5 速度/(m·s-1) 30 速度航向角/(°) 1 质量/% 10 大气密度/% 10 经度/(°) 5 纬度/(°) 5 速度倾斜角/(°) 0.1 升力系数/% 10 阻力系数/% 10
下载: 导出CSV
-
[1] LU P.Entry guidance:A unified method[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3):713-728. doi: 10.2514/1.62605 [2] 李惠峰, 张冉.再入飞行器标称迎角优化设计[J].北京航空航天大学学报, 2012, 38(8):996-1000. http://bhxb.buaa.edu.cn/CN/abstract/abstract12353.shtmlLI H F, ZHANG R.Optimal design of nominal attack of angle for re-entry vehicle[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(8):996-1000(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract12353.shtml [3] 李惠峰.高超声速飞行器制导与控制技术[M].北京:中国宇航出版社, 2012:320-325.LI H F.Guidance and control technology for hypersonic vehicle[M].Beijing:China Aerospace Publishing House, 2012:320-325(in Chinese). [4] HANSON J.Advanced guidance and control project for reusable launch vehicles:AIAA-2000-3957[R].Reston:AIAA, 2000. [5] POWELL R W.Six-degree-of-freedom guidance and control entry analysis of the HL-20[J].Journal of Spacecraft and Rockets, 1993, 30(5):537-542. doi: 10.2514/3.25563 [6] FUHRY D P.Adaptive atmospheric reentry guidance for the Kistler K-1 orbital vehicle:AIAA-1999-4211[R].Reston:AIAA, 1999. [7] LU P.Regulation about time-varying trajectories:Precision entry guidance illustrated:AIAA-1999-4070[R].Reston:AIAA, 1999. [8] LU P.An integrated approach for entry mission design and flight simulations:AIAA-2004-702[R].Reston:AIAA, 2004. [9] LU P.Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance, Control, and Dynamics, 2008, 31(4):1067-1075. doi: 10.2514/1.32055 [10] 水尊师, 周军.基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J].宇航学报, 2011, 32(6):1249-1255. http://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201106008.htmSHUI Z S, ZHOU J.On-line predictor-corrector reentry guidance law based on gauss pseudospectral method[J].Journal of Astronautics, 2011, 32(6):1249-1255(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-YHXB201106008.htm [11] 朱国栋, 沈作军.基于轨迹线性化控制的再入轨迹跟踪制导[J].北京航空航天大学学报, 2015, 41(11):1975-1982. http://bhxb.buaa.edu.cn/CN/abstract/abstract13555.shtmlZHU G D, SHEN Z J.Trajectory linearization control based tracking guidance design for entry flight[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11):1975-1982(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13555.shtml [12] 赵頔, 沈作军.基于在线轨迹迭代的自适应再入制导[J].北京航空航天大学学报, 2016, 42(7):1526-1535. http://bhxb.buaa.edu.cn/CN/abstract/abstract14012.shtmlZHAO D, SHEN Z J.Adaptive reentry guidance based on onboard trajectory iterations[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7):1526-1535(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract14012.shtml [13] 王青, 冉茂鹏.基于预测校正法的高超声速飞行器再入制导[J].北京航空航天大学学报, 2013, 39(12):1563-1567. http://bhxb.buaa.edu.cn/CN/abstract/abstract12790.shtmlWANG Q, RAN M P.Reentry guidance for hypersonic vehicle based on predictor-corrector method[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12):1563-1567(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract12790.shtml [14] 赵江, 周锐, 张超.考虑禁飞区规避的预测校正再入制导[J].北京航空航天大学学报, 2015, 41(5):864-870. http://bhxb.buaa.edu.cn/CN/abstract/abstract13247.shtmlZHAO J, ZHOU R, ZHANG C.Predictor-corrector reentry guidance satisfying no-fly zone constraints[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5):864-870(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13247.shtml [15] LU P.Entry guidance and trajectory control for reusable launch vehicle[J].Journal of Guidance, Control, and Dynamics, 1997, 20(1):143-149. doi: 10.2514/2.4008 [16] 雍恩米, 唐国金. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙: 国防科学技术大学, 2008.YONG E M, TANG G J.Trajectory optimization and guidance method for hypersonic glide reentry vehicle[D].Changsha:National University of Defense Technology, 2008(in Chinese). [17] PHILLIPS T H.A common aero vehicle (CAV) model, description, and employment guide[R].Schafer Corporation for AFRL and AFSPC, 2003. [18] XUE S, LU P.Constrained predictor-corrector entry guidance[J].Journal of Guidance, Control, and Dynamics, 2010, 33(4):1273-1280. doi: 10.2514/1.49557 [19] SHEN Z J, LU P.Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance, Control, and Dynamics, 2003, 26(1):111-121. doi: 10.2514/2.5021 [20] LZMAILOV A F, SOLODOV M V.Stabilized SQP revisited[J].Mathematical Programming, 2012, 133(1-2):93-120. doi: 10.1007/s10107-010-0413-3 [21] LU P, FORBES S, BALDWIN M.Gliding guidance of high L/D hypersonic vehicles[C]//AIAA Guidance, Navigation, and Control Conference.Reston:AIAA, 2013:1-22. [22] LU P.Entry guidance using time-scale separation in gliding dynamics[J].Journal of Spacecraft and Rockets, 2015, 52(4):1253-1258. doi: 10.2514/1.A33295 -
下载:
点击查看大图
计量
- 文章访问数: 1241
- HTML全文浏览量: 292
- PDF下载量: 586
- 被引次数: 0
