随机优化的改进交叉熵方法

任超; 张航; 李洪双

doi:10.13700/j.bh.1001-5965.2017.0017

随机优化的改进交叉熵方法

doi: 10.13700/j.bh.1001-5965.2017.0017

南京航空航天大学航空宇航学院, 南京 210016

基金项目:

南京航空航天大学研究生创新基地（实验室）开放基金 kfjj20160113

国家自然科学基金 U1533109

详细信息

作者简介:
任超, 男, 硕士研究生。主要研究方向:结构可靠性设计、灵敏度分析、随机优化方法

张航, 男, 硕士研究生。主要研究方向:结构可靠性设计、灵敏度分析、随机优化方法

李洪双, 男, 博士, 副教授, 硕士生导师。主要研究方向:飞行器可靠性设计、飞行器结构优化设计

通讯作者:
李洪双, E-mail: hongshuangli@nuaa.edu.cn

中图分类号: O224
计量
- 文章访问数: 837
- HTML全文浏览量: 106
- PDF下载量: 385
- 被引次数: 0
出版历程
- 收稿日期: 2017-01-12
- 录用日期: 2017-05-05
- 网络出版日期: 2018-01-20

Stochastic optimization method based on improved cross entropy

College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Funds:

Foundation of Graduate Innovation Center in NUAA kfjj20160113

National Natural Science Foundation of China U1533109

More Information

Corresponding author: LI Hongshuang, E-mail: hongshuangli@nuaa.edu.cn

摘要

摘要:
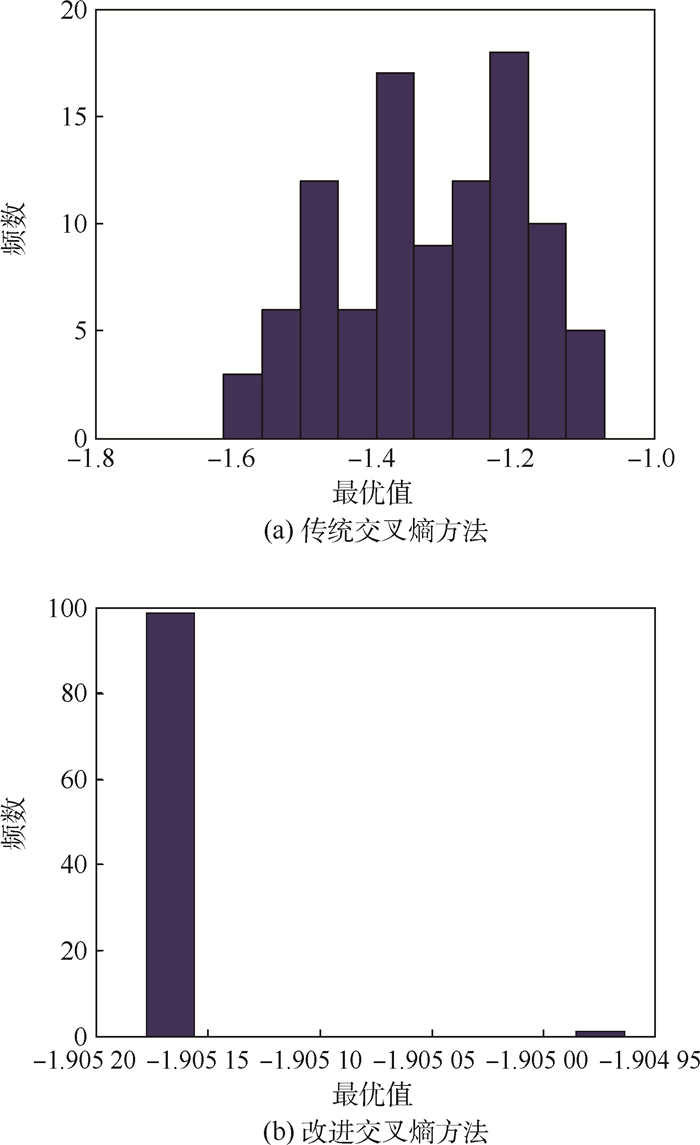
随机优化的交叉熵方法具有高效性和自适应性的特点，在高维和非线性等复杂优化问题中具有巨大的开发潜力。针对传统交叉熵优化方法精度不足的缺点，提出使用“当前精英样本”和“全局精英样本”构建新的参数更新策略，以充分提取迭代历史中的有用信息。采用自适应的平滑策略和变异操作进一步提升计算性能。通过3个计算实例证明，改进后的方法比传统交叉熵方法具有更高的计算精度和更强的全局搜索能力。
- 随机优化 /
- 交叉熵 /
- 精英样本 /
- 参数更新策略 /
- 自适应平滑策略 /
- 变异操作
Abstract:
Cross entropy method is an efficient and adaptive stochastic optimization method and has immense potential in complex optimization problems with high dimension and nonlinear constraints. However, the traditional cross entropy method is lack of accuracy. In this study, both the concepts of current elite samples and global elite samples are introduced to extract more useful information from the whole iterative history. Then, a new parameter updating strategy is established based on these two concepts. New adaptive smoothing strategy and mutation operation are also applied to improve its computing performance. The proposed algorithm is illustrated by three numerical examples. The computational results indicate that the improved cross entropy method has higher calculation accuracy and better global search capability.
- stochastic optimization /
- cross entropy /
- elite samples /
- parameter updating strategy /
- adaptive smoothing strategy /
- mutation operation

HTML全文

图 1 算例1目标函数值和最优解迭代曲线(传统交叉熵方法)

Figure 1. Iterative curves of objective function value and optimal solution for Example 1(traditional CE method)

下载: 全尺寸图片幻灯片

图 2 算例1统计结果(传统交叉熵方法)

Figure 2. Statistical results of Example 1 (traditional CE method)

下载: 全尺寸图片幻灯片

图 3 算例1目标函数值和最优解迭代曲线(变异操作)

Figure 3. Iterative curves of objective function value and optimum solution for Example 1 (with mutation operation)

下载: 全尺寸图片幻灯片

图 4 算例1统计结果(变异操作)

Figure 4. Statistical results of Example 1 (with mutation operation)

下载: 全尺寸图片幻灯片

图 5 算例1目标函数值和最优解迭代曲线(改进交叉熵方法)

Figure 5. Iterative curves of objective function value and optimal solution for Example 1(ICE method)

下载: 全尺寸图片幻灯片

图 6 算例1统计结果(改进交叉熵方法)

Figure 6. Statistical results of Example 1 (ICE method)

下载: 全尺寸图片幻灯片

图 7 算例2目标函数值和最优解迭代曲线(传统交叉熵方法)

Figure 7. Iterative curves of objective function value and optimal solution for Example 2(traditional CE method)

下载: 全尺寸图片幻灯片

图 8 算例2目标函数值和最优解迭代曲线(改进交叉熵方法)

Figure 8. Iterative curves of objective function value and optimal solution for Example 2 (ICE method)

下载: 全尺寸图片幻灯片

图 9 算例2统计结果

Figure 9. Statistical results of Example 2

下载: 全尺寸图片幻灯片

图 10 算例3统计结果

Figure 10. Statistical results of Example 3

下载: 全尺寸图片幻灯片

表 1 不同初值改进前后方法优化结果

Table 1. Optimal solutions of method before and after improvement with different initial values

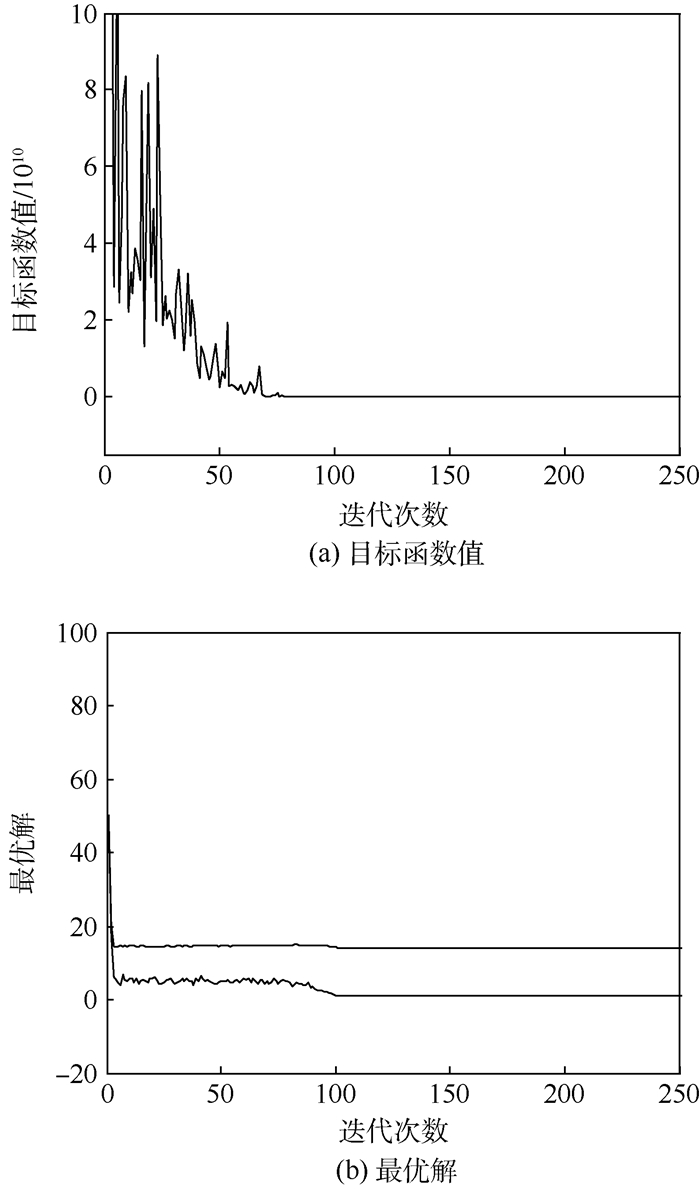
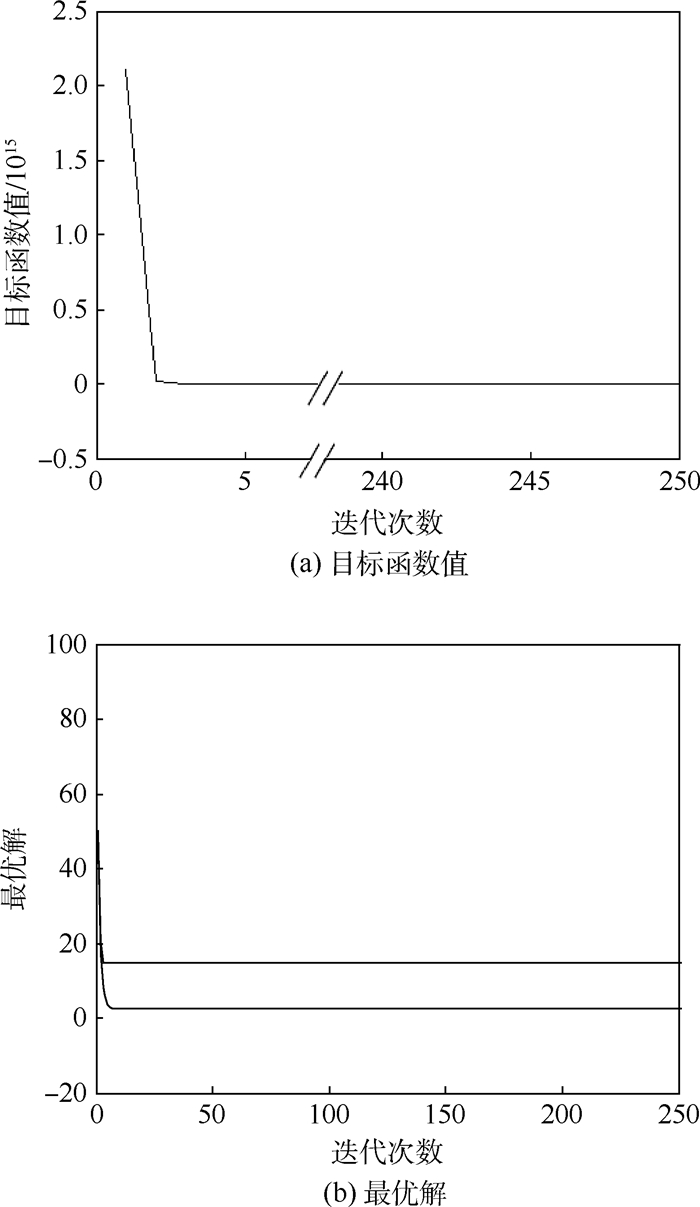
μ₀	S_CE(x^*)	S_ICE(x^*)
[56.5, 50]^T	-5 582.658 4	-6968.5867
[100, 100]^T	1.9466×10¹⁴	-6968.5868
[0, 0]^T	-6289.1210	-6968.5866
[150, 150]^T	1.1289×10¹⁶	-6968.5867
[-150, 150]^T	1.1618×10¹⁴	-6968.5868

下载: 导出CSV

表 2 传统交叉熵和改进交叉熵方法目标函数值变化过程

Table 2. Comparison of objective function value in iteration history between traditional CE and ICE methods

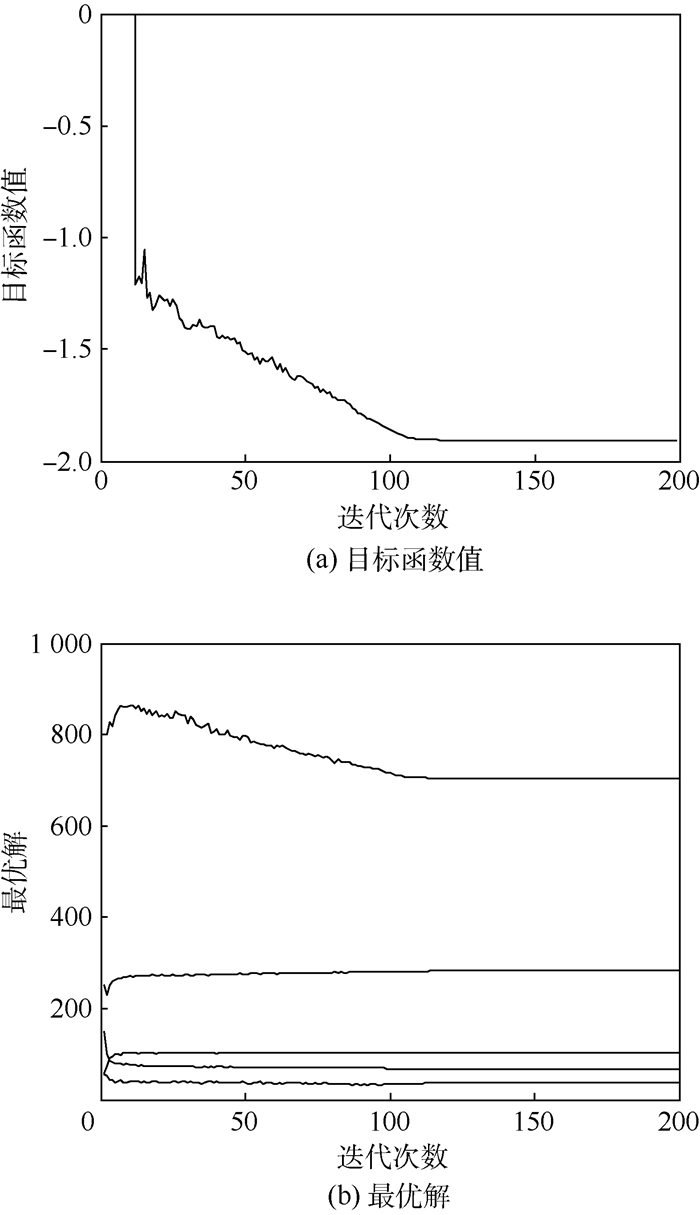
迭代次数	S_CE(x^*)	S_ICE(x^*)
1	3.046 0×10¹⁷	1.870 5×10¹⁷
2	1.885 2×10¹⁶	2.409 6×10¹⁶
3	4.116 8×10¹⁵	5.599 3×10¹⁵
4	8.374 1×10¹⁴	3.043 2×10¹⁵
5	1.273 0×10¹⁴	9.092 1×10¹⁴
6	-1.002 9	3.657 2×10¹⁴
9	-1.141 5	1.002 9×10¹³
10	-1.312 0	-0.893 3
50	-1.387 7	-1.508 1
100	-1.387 7	-1.854 4
150	-1.387 7	-1.905 2
200	-1.387 7	-1.905 2

下载: 导出CSV

参考文献(16)

[1]	HAFTKA R T, GVRDAL Z.Elements of structural optimization[M].Dordrecht:Kluwer Academic Publishers, 1990.
[2]	RUBINSTEIN R Y.Optimization of computer simulation models with rare events[J].European Journal of Operational Research, 1997, 99(1):89-112. doi: 10.1016/S0377-2217(96)00385-2
[3]	RUBINSTEIN R Y.The cross-entropy method for combinatorial and continuous optimization[J].Methodology & Computing in Applied Probability, 1999, 1(2):127-190. doi: 10.1023/A:1010091220143.pdf
[4]	HELVIK B E, WITTNER O.Using the cross-entropy method to guide/govern mobile agent's path finding in networks[M].Berlin:Springer, 2001.
[5]	ALON G, KROESE D P, RAVIV T, et al.Application of the cross-entropy method to the buffer allocation problem in a simulation-based environment[J].Annals of Operations Research, 2005, 134(1):137-151. doi: 10.1007/s10479-005-5728-8
[6]	KUO C, YEARGAIN J R, DOWNEY W J, et al.Solving the vehicle routing problem with stochastic demands using the cross-entropy method[J].Annals of Operations Research, 2005, 134(1):153-181. doi: 10.1007/s10479-005-5729-7
[7]	KROESE D P, POROTSKY S, RUBINSTEIN R Y.The cross-entropy method for continuous multi-extremal optimization[J].Methodology & Computing in Applied Probability, 2006, 8(3):383-407. doi: 10.1007/s11009-006-9753-0
[8]	HO S L, YANG S.The cross-entropy method and its application to inverse problems[J].IEEE Transactions on Magnetics, 2010, 46(8):3401-3404. doi: 10.1109/TMAG.2010.2044380
[9]	丁卫平, 王建东, 陈森博, 等.基于改进混合蛙跳算法的粗糙属性交叉熵优化约简[J].南京大学学报(自然科学), 2014, 50(2):159-166. http://doi.cnki.net/Resolution/Handler?doi=10.13232/j.cnki.jnju.2014.02.007 DING W P, WANG J D, CHEN S B, et al.Rough attribute reduction with cross-entropy based on improved shuffled frog-leaping algorithm[J].Journal of Nanjing University(Natural Sciences), 2014, 50(2):159-166(in Chinese). http://doi.cnki.net/Resolution/Handler?doi=10.13232/j.cnki.jnju.2014.02.007
[10]	李国成, 肖庆宪.求解高维函数优化问题的交叉熵蝙蝠算法[J].计算机工程, 2014, 40(10):168-174. doi: 10.3969/j.issn.1000-3428.2014.10.032 LI G C, XIAO Q X.Cross-entropy bat algorithm for solving high-dimensional function optimization problem[J].Computer Engineering, 2014, 40(10):168-174(in Chinese). doi: 10.3969/j.issn.1000-3428.2014.10.032
[11]	GHIDEY H.Reliability-based design optimization with cross-entropy method[D].Trondheim:Norwegian University of Science and Technology, 2015.
[12]	李洪双, 马远卓.结构可靠性分析与随机优化设计的统一方法[M].北京:国防工业出版社, 2015:146-147. LI H S, MA Y Z.Unified methods for structural reliability analysis and stochastic optimization design[M].Beijing:National Defense Industry Press, 2015:146-147(in Chinese).
[13]	HUI K P, BEAN N, KRAETZL M, et al.The tree cut and merge algorithm for estimation of network reliability[J].Probability in the Engineering & Informational Sciences, 2002, 17(1):23-45. https://core.ac.uk/display/12727453
[14]	吴烈. 电磁场逆问题鲁棒优化设计理论和算法研究[D]. 杭州: 浙江大学, 2012. WU L.Numerical methodologies for robust optimizations of inverse problems[D].Hangzhou:Zhejiang University, 2012(in Chinese).
[15]	LIANG J J, RUNARSSON T P, MEZURA-MONTES E, et al.Problem definitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization[R].Singapore:Nanyang Technological University, 2006.
[16]	彭宏, 杨立洪, 郑咸义, 等.计算工程优化问题的进化策略[J].华南理工大学学报(自然科学版), 1997, 25(12)17-21. doi: 10.3321/j.issn:1000-565X.1997.12.004 PENG H, YANG L H, ZHENG X Y, et al.A new evolutionary strategy for solving engineering optimization problems[J].Journal of South China University of Technology(Natural Science Edition), 1997, 25(12):17-21(in Chinese). doi: 10.3321/j.issn:1000-565X.1997.12.004