带碰撞角约束的三维有限时间滑模制导律

赵曜; 李璞; 刘娟; 陈喆; 刘向东

doi:10.13700/j.bh.1001-5965.2017.0087

带碰撞角约束的三维有限时间滑模制导律

doi: 10.13700/j.bh.1001-5965.2017.0087

赵曜^1, ,,
李璞^{1, 2},
刘娟¹,
陈喆¹,
刘向东³

1.
中国运载火箭技术研究院, 北京 100076
2.
国防科学技术大学, 长沙 410073
3.
北京理工大学自动化学院, 北京 100081

详细信息

作者简介:
赵曜男, 博士, 工程师。主要研究方向:制导及精度总体设计

通讯作者:
赵曜, E-mail:shine3y9r@126.com

中图分类号: V448
计量
- 文章访问数: 997
- HTML全文浏览量: 168
- PDF下载量: 232
- 被引次数: 31
出版历程
- 收稿日期: 2017-02-21
- 录用日期: 2017-05-05
- 网络出版日期: 2018-02-20

Finite-time sliding mode control based 3D guidance law with impact angle constraints

ZHAO Yao^{1
, ,},
LI Pu^{1, 2},
LIU Juan¹,
CHEN Zhe¹,
LIU Xiangdong³

1.
China Academy of Launch Vehicle Technology, Beijing 100076, China
2.
National University of Defense Technology, Changsha 410073
3.
School of Automation, Beijing Institute of Technology, Beijing 100081, China

More Information

Corresponding author: ZHAO Yao, E-mail:shine3y9r@126.com

摘要

摘要:
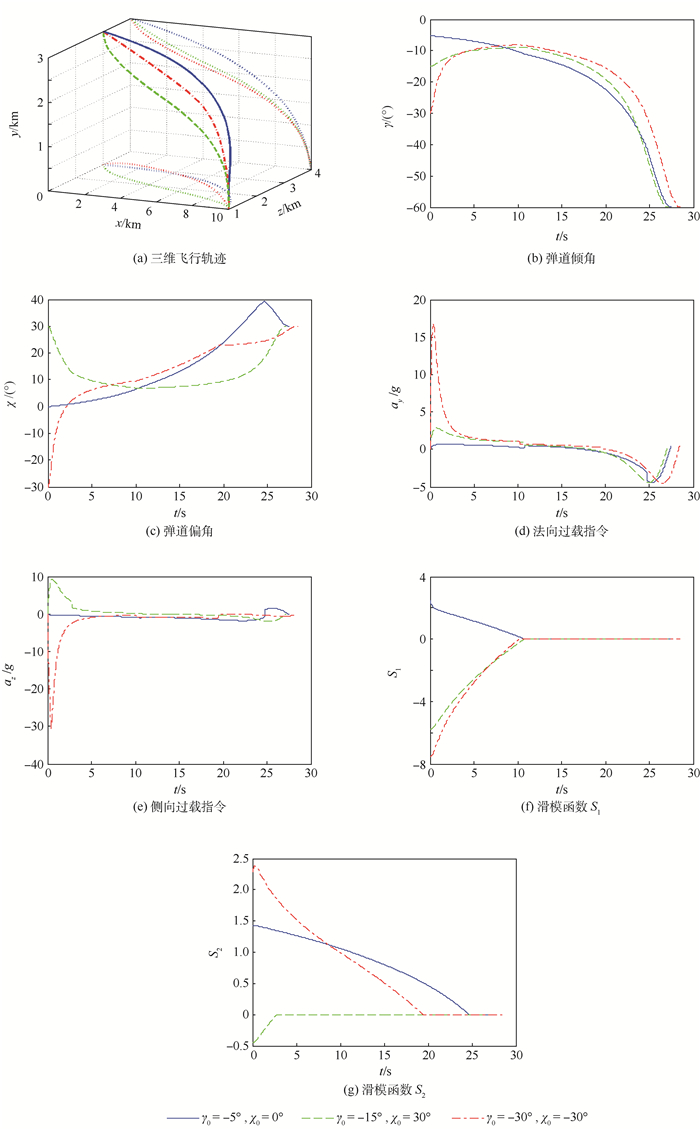
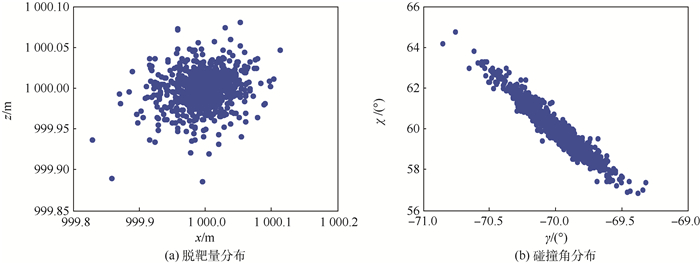
针对导弹对地面静止目标的打击问题，提出了一种三维有限时间滑模制导律。利用Lyapunov方法证明了该制导律能够控制导弹以期望的纵向和侧向碰撞角对目标进行精确打击。该方法具有以下4点优势：无需对系统模型作解耦或线性化处理，可以同时对纵向和侧向碰撞角进行约束，可以得到解析的制导指令，闭环系统对外部扰动和参数不确定性具有不敏感特性。仿真结果验证了该制导方法能够保证较高的终端精度和较强的鲁棒性。
- 制导 /
- 碰撞角约束 /
- 滑模控制 /
- 非线性 /
- 鲁棒性
Abstract:
To deal with the guidance problem of missile for intercepting ground fixed targets, a three-dimensional finite-time sliding mode control based guidance law is proposed in this paper. It is proved by the Lyapunov theory that the guidance law can steer the missile to intercept target with the desired impact angles in both azimuth and elevation. The guidance law has four advantages. First, model decoupling or model linearization is not needed in this work; second, the impact angles in both longitudinal and horizontal can be controled; third, the guidance command can be analytically derived; fourth, the closed-loop system is insensitive to external disturbance as well as parameter uncertainty. The simulation results show that high terminal accuracy and good robustness can be achieved by the proposed guidance law.
- guidance /
- impact angle constraints /
- sliding mode control /
- nonlinear /
- robustness

HTML全文

图 1 不同发射角条件下仿真结果

Figure 1. Simulation results with different launch angles

下载: 全尺寸图片幻灯片

图 2 本文制导律蒙特卡罗仿真结果

Figure 2. Results of Monte Carlo simulation with proposed guidance law

下载: 全尺寸图片幻灯片

图 3 文献[17]制导律蒙特卡罗仿真结果

Figure 3. Results of Monte Carlo simulation with guidance law in Ref. 17]

下载: 全尺寸图片幻灯片

参考文献(18)

[1]	KIM M, GRIDER K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(6):852-859.
[2]	SIOURIS G M.Missile guidance and control systems[M].Berlin:Springer, 2003.
[3]	ZARCHAN P.Tactical and strategic missile guidance[M].4th ed.Reston:AIAA, 2002.
[4]	GHAW S N, GHOSE D.Pure proportional navigation against time-varying target maneuvers[J].IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(3):1336-1346.
[5]	KIM B S, LEE J G, HAN H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1):277-288. doi: 10.1109/7.640285
[6]	JEONG S K, CHO S J, KIM E G. Angle constraint biased PNG[C]//Proceedings of 5th Asian Control Conference. Piscataway, NJ: IEEE Press, 2004: 1849-1854.
[7]	LU P, DOMAN D B, SCHIERMAN J D.Adaptive terminal guidance for hypervelocity impact in specified direction[J].Journal of Guidance, Control, and Dynamics, 2006, 29(2):269-278. doi: 10.2514/1.14367
[8]	RATNOO A, GHOSE D.Impact angle constrained interception of stationary targets[J].Journal of Guidance, Control, and Dynamics, 2008, 31(6):1816-1821.
[9]	RATNOO A, GHOSE D.Impact angle constrained guidance against nonstationary nonmaneuvering targets[J].Journal of Guidance, Control, and Dynamics, 2010, 33(1):269-275. doi: 10.2514/1.45026
[10]	ZHOU D, MU C D, XU W L.Adaptive sliding-mode guidance of a homing missile[J].Journal of Guidance, Control, and Dynamics, 1999, 22(4):589-594. doi: 10.2514/2.4421
[11]	SHIMA T.Intercept-angle guidance[J].Journal of Guidance, Control, and Dynamics, 2011, 34(2):484-492. doi: 10.2514/1.51026
[12]	TAUB I, SHIMA T.Intercept angle missile guidance under time varying acceleration bounds[J].Journal of Guidance, Control, and Dynamics, 2013, 36(3):686-699. doi: 10.2514/1.59139
[13]	HOU M Z, DUAN G R.Integrated guidance and control of homing missiles against ground fixed targets[J].Chinese Journal of Aeronautics, 2008, 21(2):162-168. doi: 10.1016/S1000-9361(08)60021-7
[14]	彭双春, 潘亮, 韩大鹏, 等.一种新型三维制导律设计的非线性方法[J].航空学报, 2010, 31(10):2018-2025. PENG S C, PAN L, HAN D P, et al.A new 3D guidance law based on nonlinear method[J].Acta Aeronautica et Astronautica Sinca, 2010, 31(10):2018-2025(in Chinese).
[15]	佘文学, 周凤岐.三维非线性变结构寻的制导律[J].宇航学报, 2004, 25(6):681-685. SHE W X, ZHOU F Q.High precision 3-D nonlinear variable structure guidance law for homing missile[J].Journal of Astronautics, 2004, 25(6):681-685(in Chinese).
[16]	OZA H B, PADHI R.Impact-angle-constrained suboptimal model predictive static programming guidance of air-to-ground missiles[J].Journal of Guidance, Control, and Dynamics, 2012, 35(1):153-164. doi: 10.2514/1.53647
[17]	RATNOO A, GHOSE D.State-dependent Riccati-equation-based guidance law for impact-angle-constrained trajectories[J].Journal of Guidance, Control, and Dynamics, 2009, 32(1):320-325. doi: 10.2514/1.37876
[18]	IMADO F, KURODA T, TAHK M J. A new missile guidance algorithm against a maneuvering target[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 1998: 145-153.

施引文献

期刊类型引用(17)

1.	王金硕，何冉，刘海平. 高超滑翔飞行器对地侦察轨迹的分段优化策略. 战术导弹技术. 2025(01): 113-125+135 . 百度学术
2.	汪馨茹，苏子康，荆献勇，曾靖轩，黄宇. 基于未知坡度倾斜跑道地形融合的无人机定点着陆轨迹优化. 战术导弹技术. 2024(06): 94-106 . 百度学术
3.	熊文祥，陈倩，汪守利，杨贵玉，杨钊. 基于二阶锥规划的飞行器滑翔段轨迹优化. 导航与控制. 2024(Z1): 129-136 . 百度学术
4.	徐慧，蔡光斌，崔亚龙，侯明哲，姚二亮. 高超声速滑翔飞行器再入轨迹优化. 哈尔滨工业大学学报. 2023(04): 44-55 . 百度学术
5.	邵雷，李明杰，赵锦. 基于局部模型的再入滑翔类飞行器轨迹在线调整算法设计. 空军工程大学学报. 2023(03): 64-72 . 百度学术
6.	王帅，杨冬，陈贵亮，唐润智. 基于自适应radau伪谱法的机械手轨迹规划方法研究. 制造业自动化. 2022(03): 103-108+117 . 百度学术
7.	周池军，邵雷，骆长鑫，李明杰，雷虎民. 高动态目标拦截弹制导与控制前沿技术展望. 空天技术. 2022(02): 61-74 . 百度学术
8.	吕名添，周祥，张洪波. 基于解析初值的滑翔飞行器轨迹快速规划方法. 宇航总体技术. 2022(04): 35-40 . 百度学术
9.	张伟，陈国明，黄威，薛辉辉. 空投变掠翼滑翔炸弹轨迹优化. 飞行力学. 2022(06): 39-43 . 百度学术
10.	宋少倩，陈永信，任鹏飞，周文勇，李伟喆. 面向航程能力的固体火箭发动机方案设计优化. 哈尔滨工业大学学报. 2022(12): 27-37 . 百度学术
11.	王培臣，张睿轩，闫循良. 不确定条件下高超声速俯冲弹道鲁棒优化. 飞控与探测. 2022(06): 61-68 . 百度学术
12.	刘平，刘航，仇国庆，刘兴高. 热率约束下高超声速飞行器Gauss时间网格参数化轨迹规划. 控制理论与应用. 2022(12): 2283-2292 . 百度学术
13.	贾高伟，王建峰. 无人机集群任务规划方法研究综述. 系统工程与电子技术. 2021(01): 99-111 . 百度学术
14.	颜楚雄，王蕴宝，秦绪国，童轶男，宋加洪. 最小动压约束下的全程轨迹优化设计方法. 导弹与航天运载技术. 2021(01): 86-90 . 百度学术
15.	任鹏飞，王洪波，周国峰，王亮，蔡强，韩英宏，余家泉，袁亚. 临近空间固体动力飞行器发动机与轨迹一体化设计优化. 推进技术. 2021(09): 1936-1947 . 百度学术
16.	陈永信. 滑翔飞行器气动外形与轨迹一体化设计优化. 空天防御. 2021(03): 76-84 . 百度学术
17.	崔乃刚，郭冬子，李坤原，韦常柱. 飞行器轨迹优化数值解法综述. 战术导弹技术. 2020(05): 37-51+75+5 . 百度学术