-
摘要:
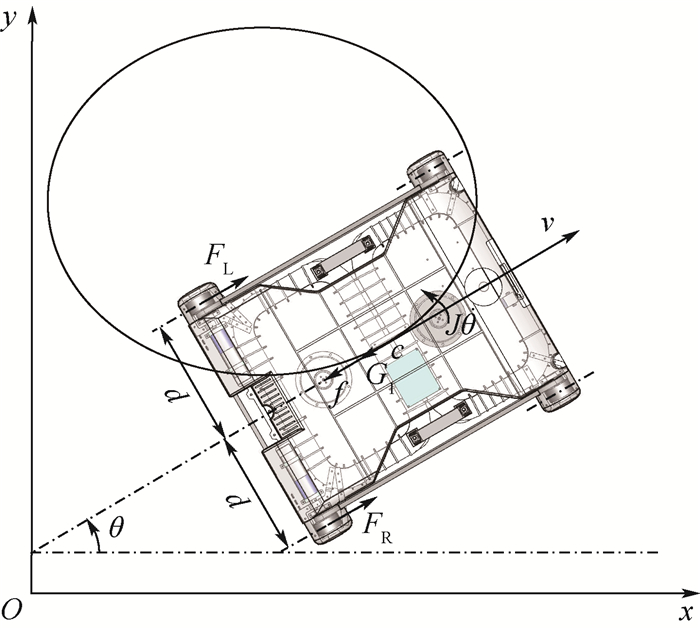
基于Udwadia-Kalaba方程建立了双腔体吸附、轮式移动爬壁机器人的解析动力学模型。将系统的预定轨迹视为系统的约束关系，巧妙地将其融合到爬壁机器人动力学建模过程中；在不出现拉格朗日乘子的条件下，获得了满足约束所需附加力矩的解析表达式及系统的解析动力学方程；采用Baumgarte约束违约稳定法抑制了由于初始条件与约束方程不相容而导致的约束违约现象。爬壁机器人的广义坐标变量变化规律和运行轨迹的数值仿真结果证明了本文建模方法的可行性和有效性。
-
关键词:
- 爬壁机器人 /
- 约束 /
- 动力学建模 /
- Udwadia-Kalaba方程 /
- Baumgarte约束违约稳定法
Abstract:With the aim of dynamic modeling of the climbing robot with dual-cavity structure and wheeled locomotion mechanism, an analytical dynamic model based on the Udwadia-Kalaba equation is established. The desired trajectory, which is regarded as constraints imposed on the system, is integrated into the dynamic modeling process of climbing robot dexterously. The explicit expression of additional torques required to satisfy constraints and explicit dynamic equation of the system without Lagrange multiplier are obtained. However, constraint violation arises when the initial conditions are incompatible with the constraint equations. Baumgarte's constraint violation stabilization method is considered for constraint violation suppression. The simulations of the varying law of the generalized coordinate variables and the trajectories are performed to demonstrate that this modeling method is feasible and effective.
-
图 2 位移的数值解与理论解对比
Figure 2. Comparison of displacements between numerical values and theoretical values
图 3 位移的数值解与理论解的误差
Figure 3. Displacement errors between numerical values and theoretical values
图 4 运行轨迹的数值解与理论解对比
Figure 4. Comparison of trajectories between numerical values and theoretical values
图 5 位移的修正数值解和理论解对比
Figure 5. Comparison of displacements between modified numerical values and theoretical values
图 6 位移误差的数值解与修正数值解对比
Figure 6. Comparison of displacement errors between numerical values and modified numerical values
图 7 运行轨迹的修正数值解与理论解对比
Figure 7. Comparison of trajectories between modified numerical values and theoretical values
-
[1] XU F, SHEN J, JIANG G P.Kinematic and dynamic analysis of a cable-climbing robot[J].International Journal of Advanced Robotic Systems, 2015, 12(7):1-17. doi: 10.5772/60865 [2] PROVANCHER W R, JENSEN-SEGAL S I, FEHLBERG M A.ROCR:An energy-efficient dynamic wall-climbing robot[J].IEEE/ASME Transactions on Mechatronics, 2011, 16(5):897-906. doi: 10.1109/TMECH.2010.2053379 [3] NAM S, OH J, LEE G, et al.Dynamic analysis during internal transition of a compliant multi-body climbing robot with magnetic adhesion[J].Journal of Mechanical Science and Technology, 2014, 28(12):5175-5187. doi: 10.1007/s12206-014-1141-z [4] BRAUN D J, GOLDFARB M.Eliminating constraint drift in the numerical simulation of constrained dynamical systems[J].Computer Methods in Applied Mechanics and Engineering, 2009, 198(37):3151-3160. http://www.sciencedirect.com/science/article/pii/S0045782509002011 [5] PAN D, GAO F, MIAO Y.Dynamic research and analyses of a novel exoskeleton walking with humanoid gaits[J].Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014, 228(9):1501-1511. doi: 10.1177/0954406213509611 [6] KORAYEM M H, SHAFEI A M.A new approach for dynamic modeling of n-viscoelastic-link robotic manipulators mounted on a mobile base[J].Nonlinear Dynamics, 2015, 79(4):2767-2786. doi: 10.1007/s11071-014-1845-8 [7] UDWADIA F E, KALABA R E.A new perspective on constrained motion[J].Proceedings:Mathematical and Physical Sciences, 1992, 439(1906):407-410. doi: 10.1098/rspa.1992.0158 [8] CHO H, YU A.New approach to satellite formation-keeping:Exact solution to the full nonlinear problem[J].Journal of Aerospace Engineering, 2009, 22(4):445-455. doi: 10.1061/(ASCE)AS.1943-5525.0000013 [9] LIU J, LIU R.Dynamic modeling of dual-arm cooperating manipulators based on Udwadia-Kalaba equation[J].Advances in Mechanical Engineering, 2016, 8(7):1-10. http://mechanicaldesign.asmedigitalcollection.asme.org/article.aspx?articleid=1732160&resultClick=1 [10] HUANG J, CHEN Y H, ZHONG Z.Udwadia-Kalaba approach for parallel manipulator dynamics[J].Journal of Dynamic Systems, Measurement, and Control, 2013, 135(6):1012-1030. http://dynamicsystems.asmedigitalcollection.asme.org/article.aspx?articleid=1732160 [11] PENNESTRI E, VALENTINI P P, DE FALCO D.An application of the Udwadia-Kalaba dynamic formulation to flexible multibody systems[J].Journal of the Franklin Institute, 2010, 347(1):173-194. doi: 10.1016/j.jfranklin.2009.10.014 [12] ZHAO H, ZHEN S, CHEN Y H.Dynamic modeling and simulation of multi-body systems using the Udwadia-Kalaba theory[J].Chinese Journal of Mechanical Engineering, 2013, 26(5):839-850. doi: 10.3901/CJME.2013.05.839 [13] BAUMGARTE J.Stabilization of constraints and integrals of motion in dynamical systems[J].Computer Methods in Applied Mechanics and Engineering, 1972, 1(1):1-16. doi: 10.1016/0045-7825(72)90018-7 [14] SCHUTTE A, UDWADIA F.New approach to the modeling of complex multibody dynamical systems[J].Journal of Applied Mechanics, 2011, 78(2):856-875. http://cat.inist.fr/?aModele=afficheN&cpsidt=23937551 [15] UDWADIA F E, KALABA R E.What is the general form of the explicit equations of motion for constrained mechanical systems[J].Journal of Applied Mechanics, 2002, 69(3):335-339. doi: 10.1115/1.1459071 [16] CHO H, UDWADIA F E.Explicit solution to the full nonlinear problem for satellite formation-keeping[J].Acta Astronautica, 2010, 67(3):369-387. http://www.sciencedirect.com/science/article/pii/S0094576510000615 -
下载:
点击查看大图
计量
- 文章访问数: 929
- HTML全文浏览量: 125
- PDF下载量: 380
- 被引次数: 0
