Feedforward decoupling and internal model control for rotor of magnetically suspended control and sensing gyroscope
-
摘要:
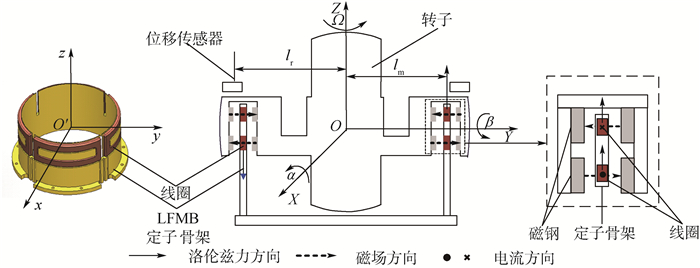
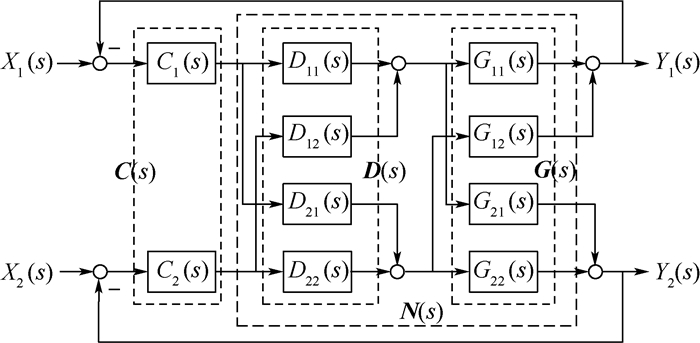
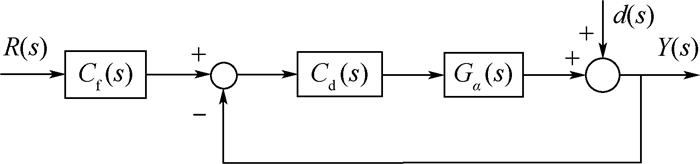
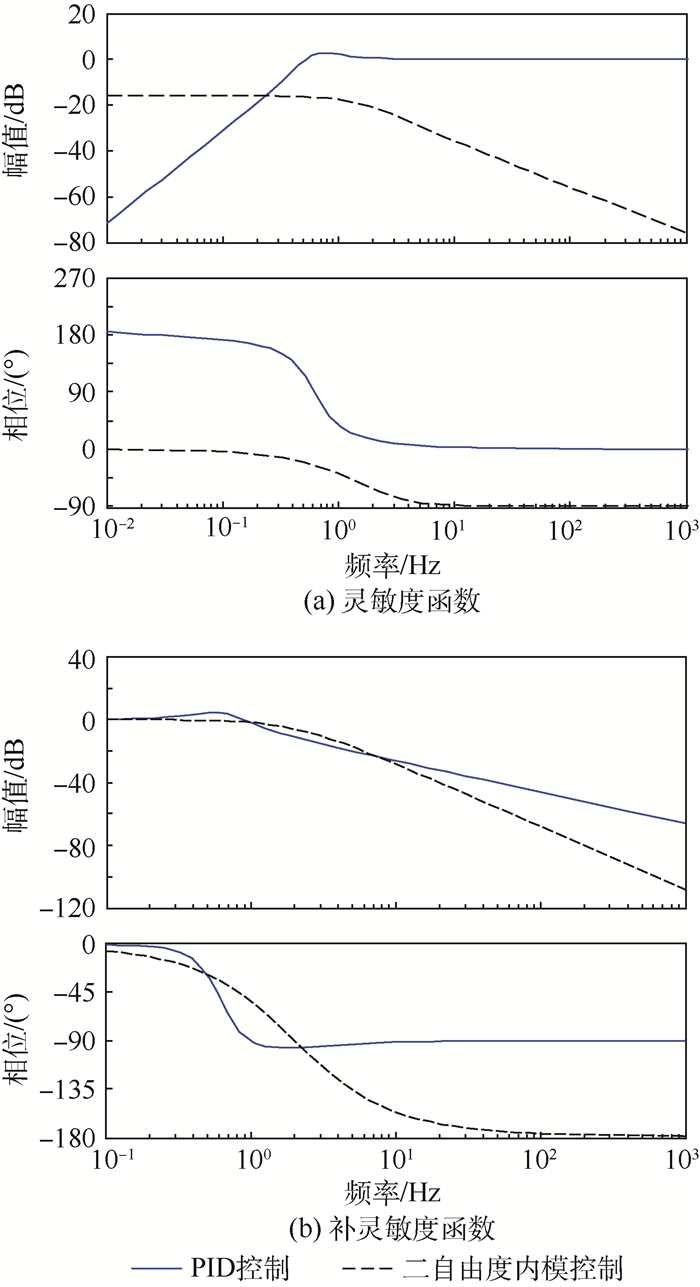
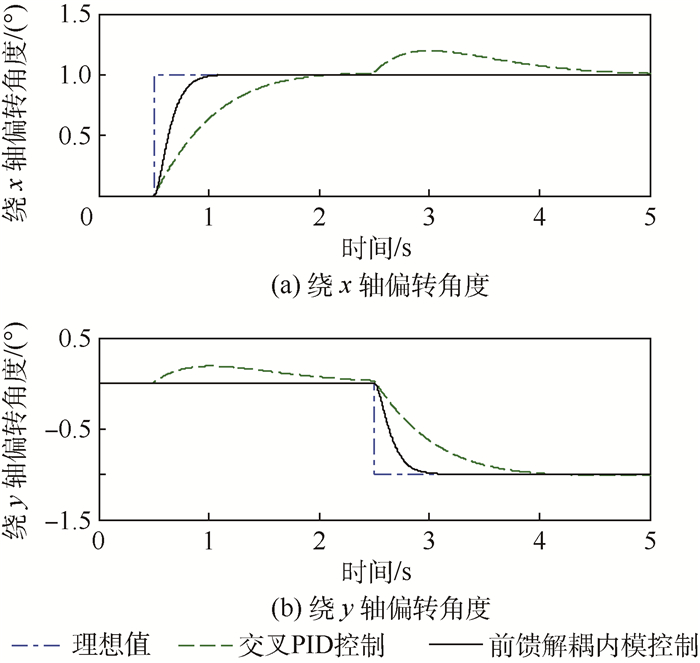
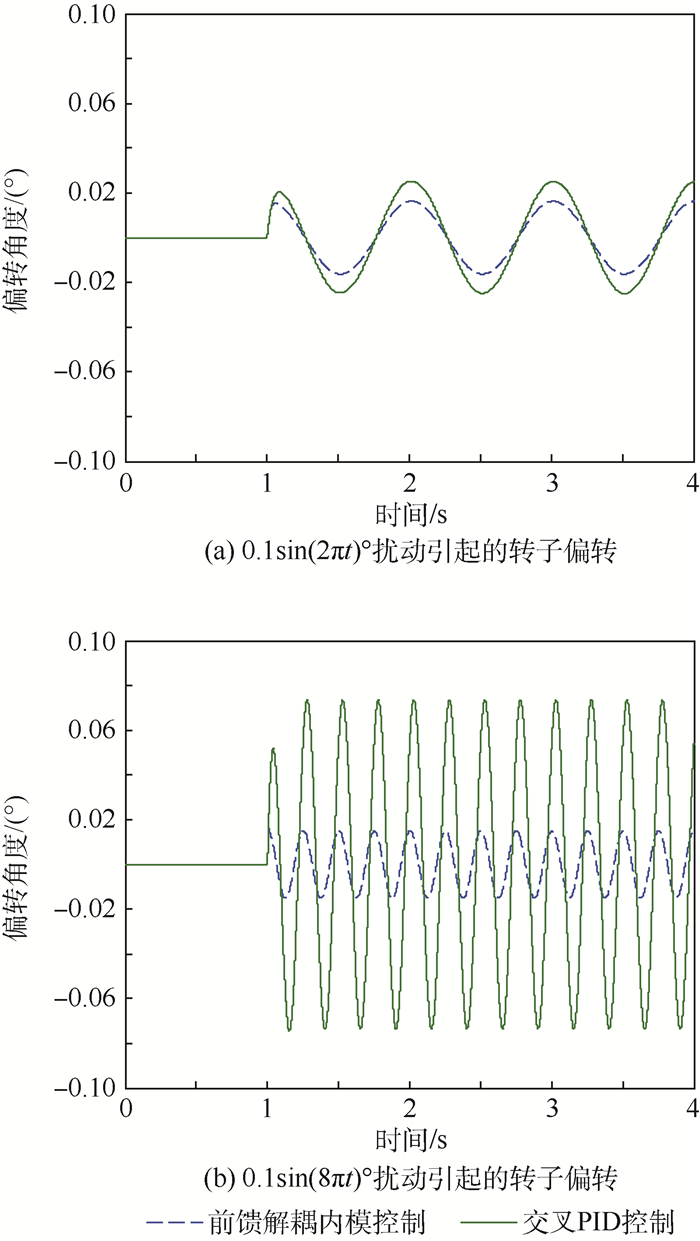
磁悬浮控制敏感陀螺以洛伦兹力磁轴承（LFMB）为力矩器驱动转子偏转。针对磁悬浮控制敏感陀螺转子径向转动自由度间存在耦合的问题以及转子偏转高精度快响应要求，提出一种前馈解耦内模控制方法。根据洛伦兹力磁轴承的工作原理建立了转子偏转动力学模型，并设计了前馈解耦矩阵实现转子径向偏转解耦，在此基础上，采用二自由度内模控制器（2-DOF IMC）对转子进行高精度快响应偏转控制。MATLAB仿真结果表明所提出的控制方法可有效实现对陀螺转子偏转的完全解耦，且转子偏转响应时间较交叉PID算法减少57.1%，受0.1sin（2π
t ）°正弦信号扰动影响产生的偏转波动幅值较交叉PID算法减少76%。-
关键词:
- 磁悬浮控制敏感陀螺 /
- 洛伦兹力磁轴承(LFMB) /
- 径向偏转 /
- 前馈解耦 /
- 二自由度内模控制
Abstract:Magnetically suspended control and sensing gyroscope takes Lorentz force magnetic bearing (LFMB) as torquer to drive the rotor to tilt. As there is coupling between the two radial rotation degrees of freedom and it requires that rotor tilts with high precision and fast response, feedforward decoupling and internal model controller is proposed. Dynamic model for rotor tilting is established based on basic structure of LFMB. Feedforward decoupling matrix is designed to perform tilting decoupling in radial direction, and then on this basis, two-degree-of-freedom internal model controller (2-DOF IMC) is adopted to perform rotor tilting control with high precision and fast response. Simulation results by MATLAB indicate that the proposed method can realize full decoupling for rotor tilting, response time is reduced by 57.1% than that of cross PID controller, and tilting fluctuation amplitude produced by 0.1sin(2π
t )° disturbance signal is reduced by 76% than that of cross PID controller. -
图 6 灵敏度函数与补灵敏度函数Bode图
Figure 6. Bode diagrams of sensitivity function and penalty sensitivity function
表 1 转子偏转系统参数
Table 1. Parameters of rotor tilting system
参数 数值 Jz/ (kg·m2) 0.016 6 Ω/Hz 100 λ2 0.003 Kp 15 Kd 3 n 200 L/m 0.115 8 kL 0.5 kH 0.2 lr/m 0.078 Jr/ (kg·m2) 0.009 7 λ1 0.08 τ/s 0.002 Ki 0.001 B/T 0.4 lm/m 0.059 ωL/Hz 80 ωH/Hz 400 kr 0.05 
下载: 导出CSV
-
[1] YU Y, FANG J, YANG Z.Torque distribution of the integrated magnetically suspended inertia actuator for attitude maneuvers[J]. Acta Astronautica, 2015, 119:71-78. https://www.sciencedirect.com/science/article/pii/S0094576515004038 [2] ABBAS H S, ALI A, HASHEMI S M, et al.LPV state-feedback control of a control moment gyroscope[J]. Control Engineering Practice, 2014, 24:129-137 doi: 10.1016/j.conengprac.2013.05.008 [3] TANG J Q, XIANG B, ZHANG Y B.Dynamic characteristics of the rotor in a magnetically suspended control moment gyroscope with active magnetic bearing and passive magnetic bearing[J]. ISA Transactions, 2014, 53(4):1357-1365. doi: 10.1016/j.isatra.2014.03.009 [4] 崔培玲, 盖玉欢, 房建成, 等.主被动磁悬浮转子的不平衡振动自适应控制[J].光学精密工程, 2015, 23(1):122-131. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gxjmgc201501017CUI P L, GAI Y H, FANG J C, et al.Adaptive control for unbalance vibration of active-passive hybrid magnetically suspended rotor[J]. Optics & Precision Engineering, 2015, 23(1):122-131(in Chinese). http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gxjmgc201501017 [5] CUI P L, LI S, ZHAO G Z, et al.Suppression of harmonic current in active-passive magnetically suspended CMG using improved repetitive controller[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(4):2132-2141. doi: 10.1109/TMECH.2016.2555858 [6] 任元, 王卫杰, 刘强, 等. 一种磁悬浮控制敏感陀螺: ZL201510006597. 5[P]. 2017-04-28.REN Y, WANG W J, LIU Q, et al. A kind of magnetically suspended control and sensing gyroscopic: ZL201510006597. 5[P]. 2017-04-28(in Chinese). [7] GERLACH B, EHINGER M, KNUT RAUE H, et al. Gimballing magnetic bearing reaction wheel with digital controller[C]//Proceedings of the 11th European Space Mechanisms and Tribology Symposium. Loutraki: European Space Agency, 2005: 35-40. http://adsabs.harvard.edu/abs/2005ESASP.591...35G [8] WANG C E, TANG J Q.Design and mathematical analysis of a novel reluctance force-type hybrid magnetic bearing for flywheel with gimballing capability[J]. Mathematical Problems in Engineering, 2013, 2013(8):147-160. https://www.researchgate.net/publication/258399423_Design_and_Mathematical_Analysis_of_a_Novel_Reluctance_Force-Type_Hybrid_Magnetic_Bearing_for_Flywheel_with_Gimballing_Capability [9] XIANG B, TANG J Q.Suspension and titling of vernier-gimballing magnetically suspended flywheel with conical magnetic bearing and Lorentz magnetic bearing[J]. Mechatronics, 2015, 28:46-54. doi: 10.1016/j.mechatronics.2015.04.008 [10] TANG J Q, XIANG B, WANG C E.Rotor's suspension for vernier-gimballing magnetically suspended flywheel with conical magnetic bearing[J]. ISA Transactions, 2015, 58:509-519. doi: 10.1016/j.isatra.2015.05.011 [11] CHEN J, LIU K, CHEN X. Modeling and low power control of active magnetic bearings system[C]//International Conference on Modelling, Identification and Control. Piscataway, NJ: IEEE Press, 2011: 319-324. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5973724 [12] BENOMAIR A M, BASHIR F A, TOKHI M O. Optimal control based LQR-feedback linearisation for magnetic levitation using improved spiral dynamic algorithm[C]//International Conference on Methods and Models in Automation and Robotics. Piscataway, NJ: IEEE Press, 2015: 558-562. http://ieeexplore.ieee.org/document/7283936/ [13] ZHANG Y C, SUN G J, ZHANG Y J. Experimental verification for zero power control of 0. 5kWh class flywheel system using magnetic bearing with gyroscopic effect[C]//Proceedings of the First International Conference on Machine Learning and Cybernetics. Piscataway, NJ: IEEE Press, 2002: 2059-2062. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1241916 [14] 孙玉坤, 朱志莹.三自由度混合磁轴承最小二乘向量机逆模辨识与解耦控制[J].中国电机工程学报, 2010, 30(15):112-117. http://www.oalib.com/paper/4400034SUN Y K, ZHU Z Y.Inverse-model identification and decoupling control based on least squres support vector machine for 3-DOF hybrid magnetic bearing[J]. Proceedings of the CSEE, 2010, 30(15):112-117(in Chinese). http://www.oalib.com/paper/4400034 [15] REN Y, FANG J.High-precision and strong-robustness control for an MSCMG based on modal separation and rotation motion decoupling strategy[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3):1539-1551. doi: 10.1109/TIE.2013.2257147 [16] 谢进进, 刘刚, 文通, 等.双框架磁悬浮控制力矩陀螺磁轴承负载力矩复合补偿的控制[J].光学精密工程, 2015, 23(8):2211-2219. http://www.eope.net/gxjmgc/article/2015/2015-8-2211.htmXIE J J, LIU G, WEN T, et al.Composite compensation for load torque of active magnetic bearing in DGMSCMG[J]. Optics and Precision Engineering, 2015, 23(8):2211-2219(in Chinese). http://www.eope.net/gxjmgc/article/2015/2015-8-2211.htm [17] KANG M S, LYOU J, LEE J K.Sliding mode control for an active magnetic bearing system subject to base motion[J]. Mechatronics, 2010, 20(1):171-178. doi: 10.1016/j.mechatronics.2009.09.010 [18] PENG C, FANG J, XU X.Mismatched disturbance rejection control for voltage-controlled active magnetic bearing via state-space disturbance observer[J]. IEEE Transactions on Power Electronics, 2015, 30(5):2753-2762. doi: 10.1109/TPEL.2014.2352366 [19] ZHENG S, HAN B, GUO L.Composite hierarchical antidisturbance control for magnetic bearing system subject to multiple external disturbances[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12):7004-7012. doi: 10.1109/TIE.2014.2316226 [20] 吴鹏松, 吴朝野, 周东华.信号解耦控制系统分析[J].控制工程, 2013, 20(3):471-474. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jczdh201303021WU P S, WU C Y, ZHOU D H.Analysis of signal decoupling control system[J]. Control Engineering of China, 2013, 20(3):471-474(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jczdh201303021 [21] OKAJIMA H, MATSUNAGA N, KAWAJI S.Design of dynamic quantizers for 2-DOF IMC and its application to the temperature control of a heat plate[J]. SICE Journal of Control Measurement & System Integration, 2011, 4(1):77-82. https://www.researchgate.net/publication/258496327_Design_of_Dynamic_Quantizers_for_2-DOF_IMC_and_Its_Application_to_the_Temperature_Control_of_a_Heat_Plate [22] OKAJIMA H, UMEMOTO T, MATSUNAGA N, et al. Analysis of dynamic quantizer in 2-DOF internal model control system with dead-time[C]//ICCAS-SICE, 2009. Piscataway, NJ: IEEE Press, 2009: 4380-4383. http://ieeexplore.ieee.org/document/5332886/ [23] 辛朝军, 蔡远文, 任元, 等.磁悬浮敏感陀螺动力学建模与关键误差源分析[J].北京航空航天大学学报, 2016, 42(10):2048-2058. http://bhxb.buaa.edu.cn/CN/abstract/abstract13745.shtmlXIN C J, CAI Y W, REN Y, et al.Dynamic modeling and key error sources analysis of magnetically suspended sensitive gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10):2048-2058(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13745.shtml [24] 房建成, 孙津济, 樊亚洪.磁悬浮惯性动量轮技术[M].北京:国防工业出版社, 2012:279-280.FANG J C, SUN J J, FAN Y H.Magnetically suspended inertial momentum wheel technology[M]. Beijing:National Defense Industry Press, 2012:279-280(in Chinese). [25] 房建成, 任元.磁悬浮控制力矩陀螺技术[M].北京:国防工业出版社, 2014:107-120.FANG J C, REN Y.Magnetically suspended control momentum gyroscope technology[M]. Beijing:National Defense Industry Press, 2014:107-120(in Chinese). -
下载:
点击查看大图
图(9) / 表(1)
计量
- 文章访问数: 703
- HTML全文浏览量: 56
- PDF下载量: 382
- 被引次数: 0
