-
摘要:
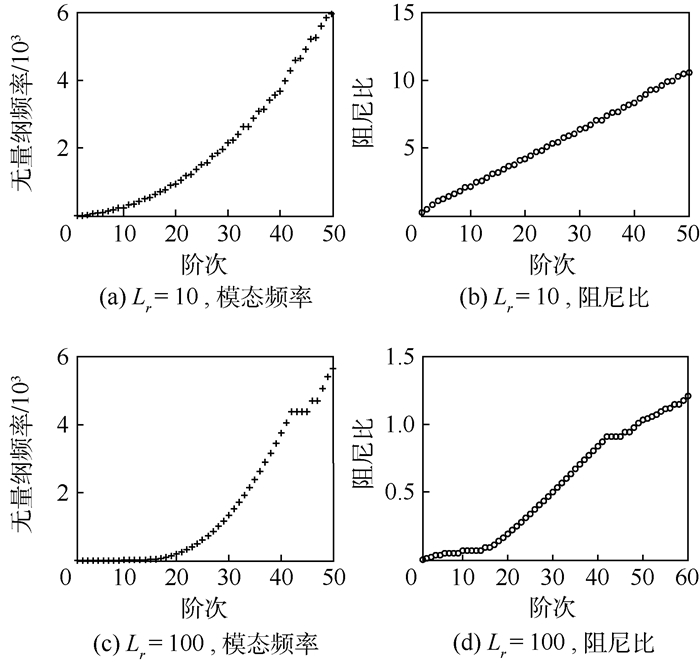
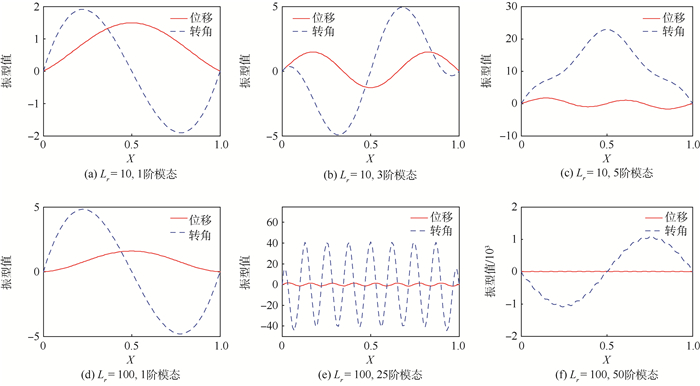
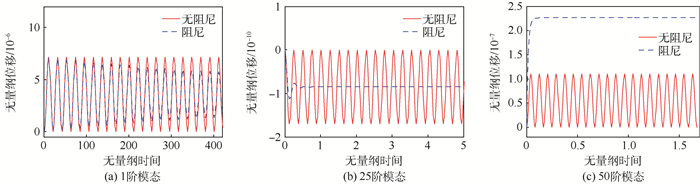
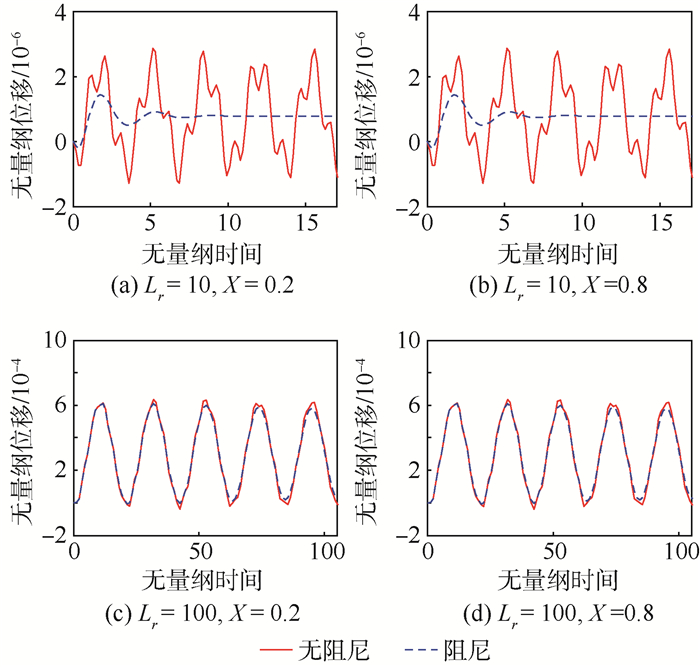
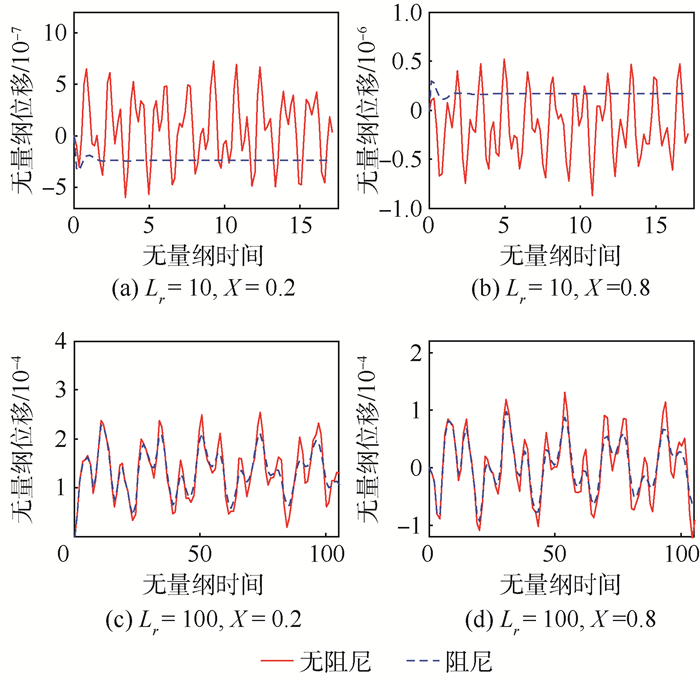
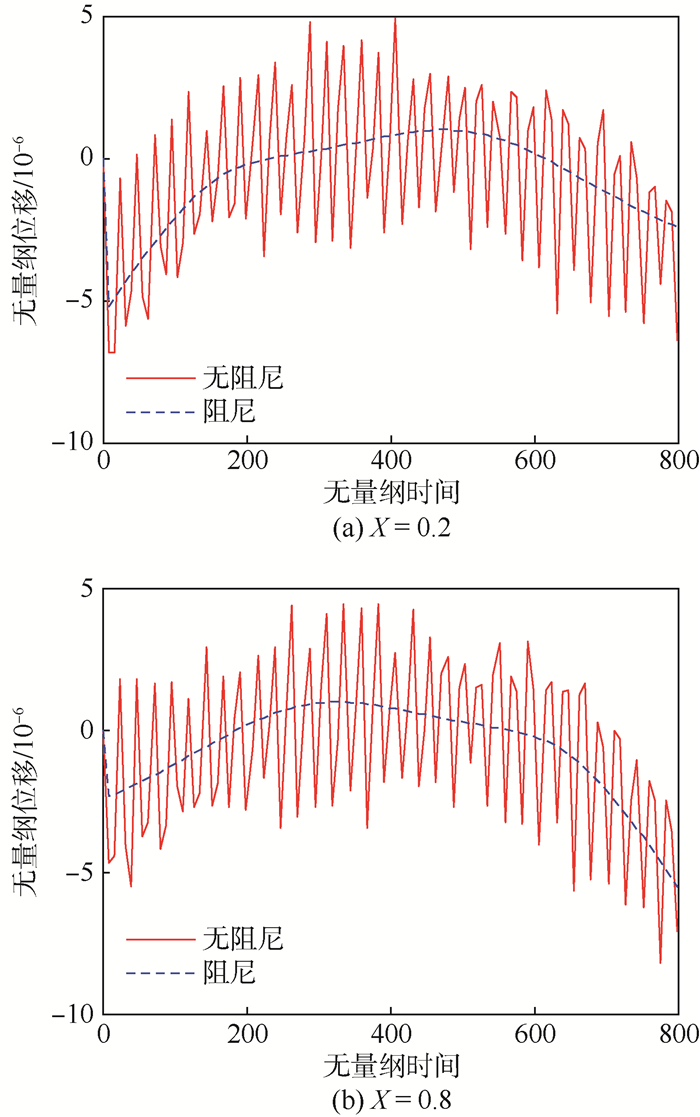
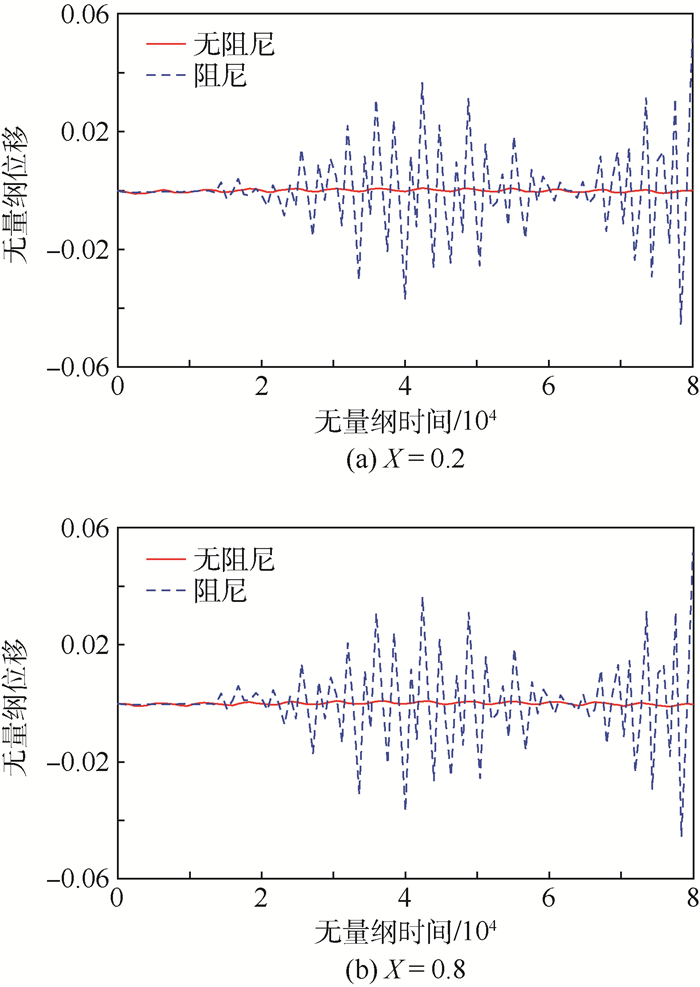
基于铁木辛柯梁理论，对两端固支梁在承受阶跃载荷和移动载荷下的响应进行了分析。借助K-V阻尼模型，研究了阻尼对系统动态性能的影响。为了进行理论求解，推导了比例阻尼的使用条件，继而运用实模态叠加法理论，最终导出了系统受载时响应的解析解。数值分析结果表明，该方法准确可靠，为其他数值算法，如拉普拉斯变换法，提供了横向对比的依据。有阻尼振动的分析表明系统在高阶模态具有过临界阻尼特性，在低阶模态为收敛振荡特性。阻尼对系统的响应有很大影响，尤其在大长细比时，甚至出现了振幅增大的情形。此外，在阶跃载荷的作用下，系统均呈现出了低频模态为主的响应特性。
Abstract:Based on Timoshenko beam theory, this paper has analyzed the dynamic properties when a clamped beam subjected to step load and moving load respectively. In addition, K-V damping model is considered to study the influence of damping on dynamic performance of the system. To acquire the theoretical solution, proportional damping utilization condition is derived, the real modal superposition method is applied, and eventually obtain the analytical responses when beam subjected to external loads. The numerical analysis results indicate that the solving process is accurate and reliable, providing a measurement reference to other methods, like Laplace transformation. The results of damping cases demonstrate that the high modes inherit over damping property, while in low modes present oscillation convergent characteristic. Sometimes, the damping can have significantly impact on the whole system, and for large slender ratios, the amplitude under moving load is even enlarged. Furthermore, the dynamic response subjected to step load is dominated by the low modes.
-
Key words:
- Timoshenko beam /
- K-V damping /
- real mode theory /
- step load /
- moving load
-
图 1 Durbin数值反拉普拉斯求解效果示意图
Figure 1. Schematic of solving accuracy of Durbin's inverse Laplace
图 6 d*=0.5时无量纲位移总响应
Figure 6. Non-dimensionalized response of total displacement when d*=0.5
图 7 d*=0.25时无量纲位移总响应
Figure 7. Non-dimensionalized response of total displacement when d*=0.25
图 8 Lr=10无量纲位移总响应
Figure 8. Non-dimensionalized response of total displacement when Lr=10
-
[1] LABUSCHAGNE A, RENSBURG N F J V, MERWE A J V D.Comparison of linear beam theories[J].Mathematical & Computer Modelling, 2009, 49(1-2):20-30. https://www.sciencedirect.com/science/article/pii/S0895717708002112 [2] STEPHEN N G.The second spectrum of Timoshenko beam theory-Further assessment[J].Journal of Sound and Vibration, 2006, 292(1-2):372-389. doi: 10.1016/j.jsv.2005.08.003 [3] HAN S M, BENAROYA H, WEI T.Dynamics of transversely vibrating beams using four engineering theories[J].Journal of Sound and Vibration, 1999, 225(5):935-988. doi: 10.1006/jsvi.1999.2257 [4] KOCATVRK T, ÇIM ÇEK M.Dynamic analysis of eccentrically prestressed viscoelastic Timoshenko beams under a moving harmonic load[J].Computers & Structures, 2006, 84(31):2113-2127. https://www.sciencedirect.com/science/article/pii/S0045794906002744 [5] BOLEY B, CHAO C.Some solutions of the timoshenko beam equations[J].Journal of Applied Mechanics, 1955, 25:579-586. http://www.worldcat.org/title/some-solutions-of-the-timoshenko-beam-equations/oclc/43827789 [6] XIN Y F, SONG Y C, ZHU D C, et al.Elastic impact on finite Timoshenko beam[J].Acta Mechanica Sinica (English Series), 2002, 18(3):252-263. doi: 10.1007/BF02487953 [7] 邢誉峰.有限长Timoshenko梁弹性碰撞接触瞬间的动态特性[J].力学学报, 1999, 31(1):68-74. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lxxb199901008XIN Y F.The characteristics of Timoshenko beam during the process of elastic impact and contact[J].Acta Mechanica Sinica, 1999, 31(1):68-74(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lxxb199901008 [8] SU Y C, MA C C.Transient wave analysis of a cantilever Timoshenko beam subjected to impact loading by Laplace transform and normal mode methods[J].International Journal of Solids & Structures, 2012, 49(9):1158-1176. http://www.sciencedirect.com/science/article/pii/S0020768312000297 [9] SU Y C, MA C C.Theoretical analysis of transient waves in a simply-supported Timoshenko beam by ray and normal mode methods[J].International Journal of Solids & Structures, 2011, 48(3):535-552. http://www.sciencedirect.com/science/article/pii/S0020768310003756 [10] HU M Y, WANG A W, ZHANG X M.Approximate analytical solutions and experimental analysis for transient response of constrained damping cantilever beam[J].Applied Mathematics and Mechanics, 2010, 31(11):1359-1370. doi: 10.1007/s10483-010-1368-9 [11] CHEN W R.Parametric studies on bending vibration of axially-loaded twisted Timoshenko beams with locally distributed Kelvin-Voigt damping[J].International Journal of Mechanical Sciences, 2014, 88:61-70. doi: 10.1016/j.ijmecsci.2014.07.006 [12] GU L L, QIN Z Y, CHU F L.Analytical analysis of the thermal effect on vibrations of a damped Timoshenko beam[J].Mechanical Systems & Signal Processing, 2014, 60-61:619-643. https://www.sciencedirect.com/science/article/pii/S0888327014004634 [13] ZHANG X Y, ZHU M, LIANG H Q. Dynamic analysis of the continuous fluid-structure system based on Timoshenko model and considering damping: AIAA-2017-1984[R]. Reston: AIAA, 2017. https://www.researchgate.net/publication/313455622_Dynamic_analysis_of_the_continuous_fluid-structure_system_based_on_Timoshenko_model_and_considering_damping [14] DUBNER H, ABATE J.Numerical inversion of Laplace transforms by relating them to the finite Fourier cosine transform[J].Journal of the ACM, 1968, 15(1):115-123. doi: 10.1145/321439.321446 [15] DURBIN F.Numerical inversion of Laplace transforms:An efficient improvement to Dubner and Abate's method[J].Computer Journal, 1974, 17(4):371-376. doi: 10.1093/comjnl/17.4.371 [16] JENSEN J J.On the shear coefficient in Timoshenko's beam theory[J].Journal of Applied Mechanics, 1966, 33(2):621-635. https://www.sciencedirect.com/science/article/pii/0022460X83905114 [17] ZHAO H L, LIU K S, ZHANG C G.Stability for the Timoshenko beam system with local Kelvin-Voigt damping[J].Acta Mathematica Sinica(English Series), 2005, 21(3):655-666. doi: 10.1007/s10114-003-0256-4 [18] CAPSONI A, VIGANÒG M, BANI-HANI K.On damping effects in Timoshenko beams[J].International Journal of Mechanical Sciences, 2013, 73(8):27-39. https://www.sciencedirect.com/science/article/pii/S0020740313001161 -
下载:
点击查看大图
计量
- 文章访问数: 838
- HTML全文浏览量: 109
- PDF下载量: 421
- 被引次数: 0
