-
摘要:
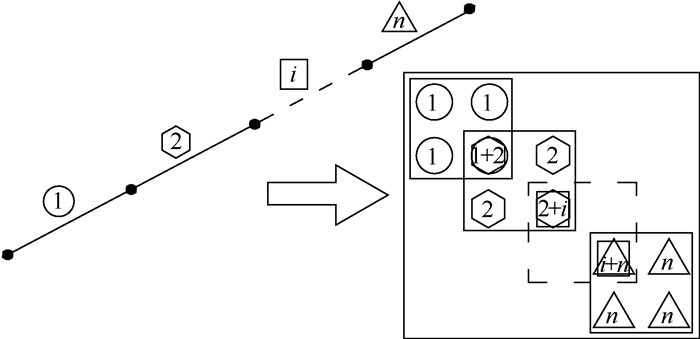
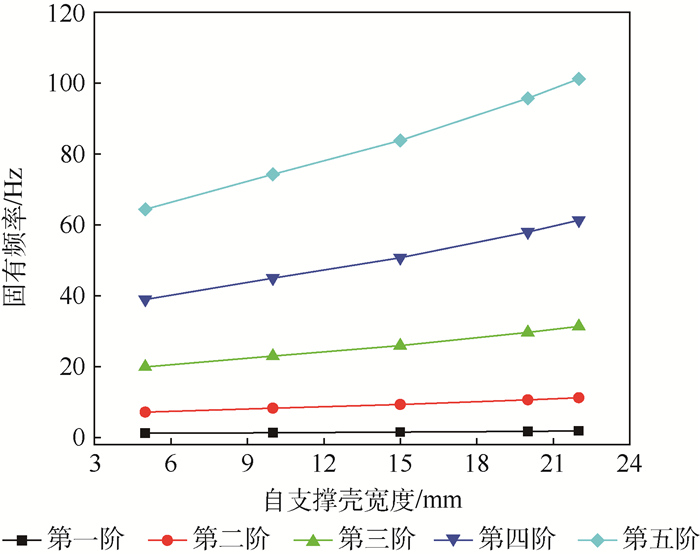
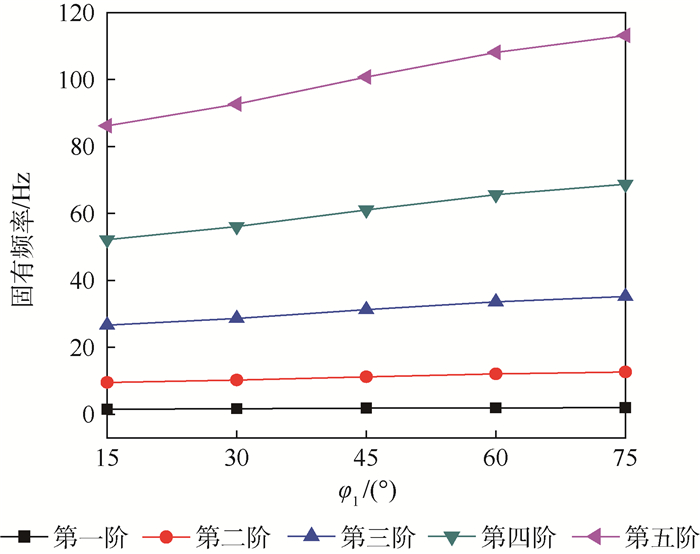
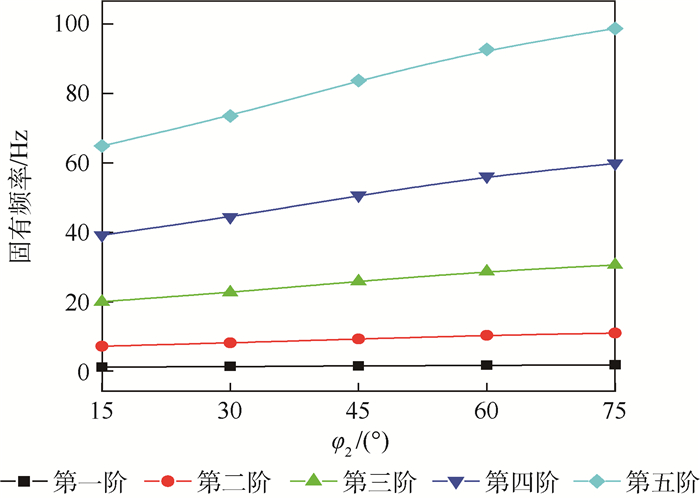
充气展开自支撑臂是由层合铝膜和离散自支撑壳组成，可在无充气压力下实现对有效载荷的支撑。为提高充气展开自支撑臂振动特性预测精度，首先，基于Timoshenko梁理论和哈密顿原理，推导了自支撑臂振动微分方程，提出了考虑充气压力的预应力和构型变化的梁单元模型。该单元模型考虑了结构自支撑壳的离散分布特性，使建立的质量矩阵更接近自支撑臂结构的真实值。然后，通过实验对该模型进行验证，结果表明本文方法比传统梁单元模型具有更好的精度。最后，分析了充气压力和自支撑壳宽度等参数对自支撑臂结构振动模态的影响规律，结果可为充气展开自支撑臂的设计提供理论参考。
Abstract:The inflatable self-supporting boom, which is made of laminated aluminum film and local discrete self-supporting thin shell, has the ability to support the effective load at zero inner pressure. In order to improve the accuracy predicting the vibration characteristics of the inflatable self-supporting boom, the vibration differential equation of the self-supporting boom was first deduced based on the Timoshenko beam theory and Hamiltonian principle, and a new beam element model considering the prestress and configuration change for inflation pressure was proposed. Moreover, this beam element model also considers the discrete characteristics of the self-supporting shell in self-supporting boom, and the mass matrix established by this model is closer to true value. Then, this beam element model is verified by the vibration test results, and the verified results show that this model has better accuracy than the traditional beam element model. Finally, the influence of the inflatable pressure and the width of self-supporting shell on the vibration characteristics of the self-supporting booms is analyzed. This study would provide a theoretical reference for the design of the inflatable self-supporting boom.
-
Key words:
- deployable structure /
- self-supporting /
- inflatable structures /
- prestress /
- vibration mode
-
图 3 整体刚度矩阵或质量矩阵的组装方法
Figure 3. Assembly method of global stiffness matrix or mass matrix
图 4 本文方法和ANSYS Beam188的基频求解偏差随长细比的变化曲线
Figure 4. Variation curve of the first natural frequency solving deviation of proposed method and ANSYS Beam188 with slenderness ratios
图 5 自支撑臂固有频率随充气压力的变化曲线
Figure 5. Variation curves of self-supporting boom's natural frequency with internal pressure
图 7 自支撑壳宽度对自支撑臂固有频率的影响曲线
Figure 7. Effect curves of width of self-supporting shell on natural frequency of self-supporting boom
图 8 自支撑壳个数对自支撑臂固有频率的影响曲线
Figure 8. Effect curves of number of self-supporting shell on natural frequency of self-supporting boom
图 9 6个自支撑壳的自支撑臂截面示意图
Figure 9. Schematic of cross-section of self-supporting boom with six self-supporting shells
图 10 自支撑臂固有频率随φ1的变化曲线(φ2=90°)
Figure 10. Variation curves of self-supporting boom's natural frequency with φ1(φ2=90°)
图 11 自支撑臂固有频率随φ2的变化曲线(φ1=0°)
Figure 11. Variation curves of self-supporting boom's natural frequency with φ2(φ1=0°)
表 1 自支撑臂振动模态对比
Table 1. Comparison of self-supporting boom's vibration mode
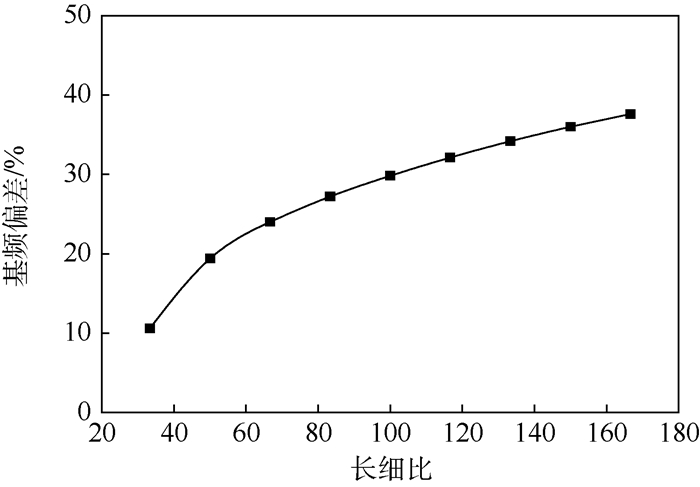
充气压力/kPa 结构基频/Hz 偏差/% 实验[26] Beam188 本文方法 Beam188与实验偏差 本文方法与实验偏差 0 17.55 20.23 18.38 15.27 4.73 10 17.70 20.64 18.77 16.61 6.05 20 17.70 21.04 19.16 18.87 8.25 30 17.71 21.44 19.53 21.06 10.28 40 17.98 21.82 19.90 21.36 10.68 
下载: 导出CSV
表 2 层合铝膜的材料属性
Table 2. Material properties of laminated aluminum membrane
参数 厚度/mm 弹性模量/GPa 泊松比 密度/(kg·m-3) 数值 0.1 12.36 0.3 1 960
下载: 导出CSV
表 3 自支撑壳的材料属性
Table 3. Material properties of self-supporting shell
参数 宽度/mm 厚度/mm 弹性模量/GPa 泊松比 密度/(kg·m-3) 数值 15 0.2 150 0.3 4 535
下载: 导出CSV
-
[1] FELLINI R A, KROPP Y L.James Webb space telescope sunshield:Challenges in analysis of gossamer structures[J].Technology Review Journal, 2008, 16(1):17-44. [2] AAROHI V. Lightweight, high-performance solar cells for high power-to-weight and deployable solar arrays: AIAA-2016-5283[R]. Reston: AIAA, 2016. [3] 刘龙斌, 吕明云, 肖厚地, 等.基于压差梯度的平流层飞艇艇囊应力计算和仿真[J].北京航空航天大学学报, 2014, 40(10):1386-1391.LIU L B, LÜ M Y, XIAO H D, et al.Calculation and simulation of stratospheric airship capsule stress considering the pressure gradient[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10):1386-1391(in Chinese). [4] 卫剑征, 谭惠丰, 王伟志, 等.充气式再入减速器研究最新进展[J].宇航学报, 2013, 34(7):881-890.WEI J Z, TAN H F, WANG W Z, et al.New trends in inflatable re-entry aeroshell[J].Journal of Astronautics, 2013, 34(7):881-890(in Chinese). [5] JOSHUA B, GRANT S, JUSTIN K, et al. An investigation of three-dimensional flow over an undulating inflatable wing: AIAA-2016-0593[R]. Reston: AIAA, 2016. doi: 10.2514/6.2016-0593 [6] TAN D, YANG Z.Deployment simulation and comparison of inflatable antenna beam with different folded configurations[J].International Journal of Applied Electromagnetics and Mecha-nics, 2010, 33(3):1513-1527. [7] 曹旭, 王伟志, 张宏伟, 等.一种新型充气式重力梯度杆的研制和在轨展开试验[J].航天返回与遥感, 2014, 35(3):20-27.CAO X, WANG W Z, ZHANG H W, et al.Development and space experiment of a new inflatable gravity gradient boom[J].Spacecraft Recovery and Remote Sensing, 2014, 35(3):20-27(in Chinese). [8] WEI J, TAN H, WANG W, et al.Deployable dynamic analysis and on-orbit experiment for inflatable gravity-gradient boom[J].Advances in Space Research, 2015, 55(2):639-646. doi: 10.1016/j.asr.2014.10.024 [9] COMER R L, LEVY S.Deflections of an inflated circular-cylindrical cantilever beam[J].AIAA Journal, 1963, 1(7):1652-1654. doi: 10.2514/3.1873 [10] MAIN A, PETERSON S W, STRAUSS A M.Load deflection behaviour of space-based inflatable beams[J].Journal of Aerospace Engineering, 1994, 7(2):225-238. doi: 10.1061/(ASCE)0893-1321(1994)7:2(225) [11] LIU Y P, WANG C G, TAN H F.The interactive bending wrin-kling behaviour of inflated beams[J].Proceedings of the Royal Society A-Mathematical, Physical and Engineering Sciences, 2016, 472(2193):20160504. doi: 10.1098/rspa.2016.0504 [12] 杜振勇. 充气梁弯皱特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.DU Z Y. Research on bending-wrinkling characteristics of inflated beams[D]. Harbin: Harbin Institute of Technology, 2012(in Chinese). [13] THOMAS J, BLOCH A.Non linear behaviour of an inflatable beam and limit states[J].Procedia Engineering, 2016, 155:398-406. doi: 10.1016/j.proeng.2016.08.043 [14] ELSABBAGH A.Nonlinear finite element model for the analysis of axisymmetric inflatable beams[J].Thin-Walled Structures, 2015, 96:307-313. doi: 10.1016/j.tws.2015.08.021 [15] 夏人伟.自适应结构综述[J].北京航空航天大学学报, 1999, 25(6):623-628.XIA R W.Overview of adaptive strusture[J].Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(6):623-628(in Chinese). [16] 卫剑征, 毛丽娜, 杜星文.空间卷曲折叠管充气控制展开动力学研究[J].工程力学, 2009, 26(1):227-232.WEI J Z, MAO L N, DU X W.Study for inflatable control deployment dynamics of rolled booms[J].Engineering Mecha-nics, 2009, 26(1):227-232(in Chinese). [17] 徐彦, 关富玲.可展开薄膜结构折叠方式和展开过程研究[J].工程力学, 2008, 25(5):176-181.XU Y, GUAN F L.Fold methods and deployment analysis of deployable membrane structure[J].Engineering Mechanics, 2008, 25(5):176-181(in Chinese). [18] MAIN J A, CARLIN R A, GARCIA E, et al.Dynamic analysis of space-based inflated beam structures[J].Journal of the Acoustical Society of America, 1995, 97(2):1035-1045. doi: 10.1121/1.412216 [19] 谭惠丰, 李云良, 毛丽娜, 等.空间充气展开支撑管的自振特性研究[J].哈尔滨工业大学学报, 2008, 40(5):709-713. http://www.cnki.com.cn/Article/CJFDTotal-ZDZC201506019.htmTAN H F, LI Y L, MAO L N, et al.Free vibration characteristics of inflatable supporting tube[J].Journal of Harbin Institute of Technology, 2008, 40(5):709-713(in Chinese). http://www.cnki.com.cn/Article/CJFDTotal-ZDZC201506019.htm [20] 刘福寿. 大型空间结构动力学等效建模与振动控制研究[D]. 南京: 南京航空航天大学, 2015: 49-74.LIU F S. Dynamic equivalent modeling and vibration control of large space structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 49-74(in Chinese). [21] JHA A, INMAN D.Importance of geometric non-linearity and follower pressure load in the dynamic analysis of a gossamer structure[J].Journal of Sound and Vibration, 2004, 278(1-2):207-231. doi: 10.1016/j.jsv.2003.10.026 [22] APEDO K L, RONEL S, JACQUELIN E, et al.Free vibration analysis of inflatable beam made of orthotropic woven fabric[J].Thin-Walled Structures, 2014, 78:1-15. doi: 10.1016/j.tws.2013.12.004 [23] THOMAS J C, JIANG Z, WIELGOSZ C.Continuous and finite element methods for the vibrations of inflatable beams[J].International Journal of Space Structures, 2006, 21(4):197-222. doi: 10.1260/026635106780866033 [24] COWPER G R.The shear coefficient in Timoshenko's beam theory[J].Journal of Applied Mechanics, 1967, 33(2):335-340. [25] PRZEMIENIECKI J S. Theory of matrix structural analysis[M].New York:McGraw-Hill, 1968:388-391. [26] 宋博. 充气展开自支撑结构力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 50-62.SONG B. Research of mechanical properties of inflatable self-supporting structure[D]. Harbin: Harbin Institute of Technology, 2015: 50-62(in Chinese). [27] WEI J Z, TAN H F, YU J X, et al.Dynamic testing and analysis of inflatable beams[J].Applied Mechanics and Materials, 2012, 226-228:546-552. doi: 10.4028/www.scientific.net/AMM.226-228 期刊类型引用(2)
1. 院老虎，康雪，连冬杉，陈源强，翟柯嘉. 空间薄膜结构充气展开研究. 南京航空航天大学学报. 2021(01): 27-34 . 
百度学术2. 徐宁，刘平，黄杨成，孙凯，仓杰卿. 竖向加载下的悬臂式气肋结构变形研究. 空间结构. 2021(04): 43-49 . 百度学术其他类型引用(1)
-
下载:
百度学术
点击查看大图
计量
- 文章访问数: 757
- HTML全文浏览量: 79
- PDF下载量: 618
- 被引次数: 3
