Design of decoupling controller for spinning missile based on receding horizon optimization
-
摘要:
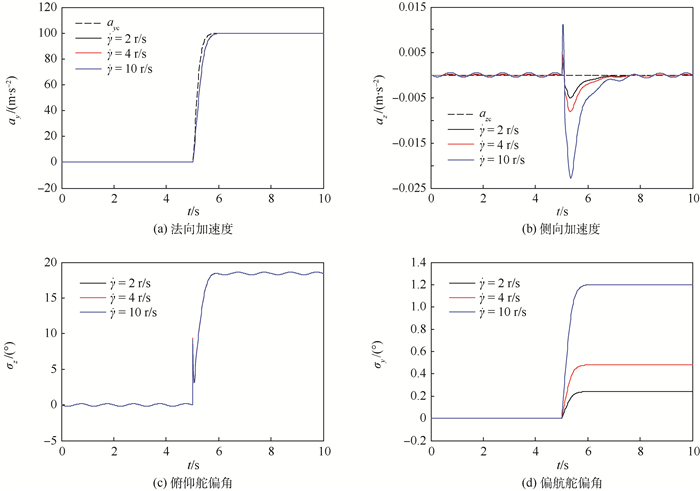
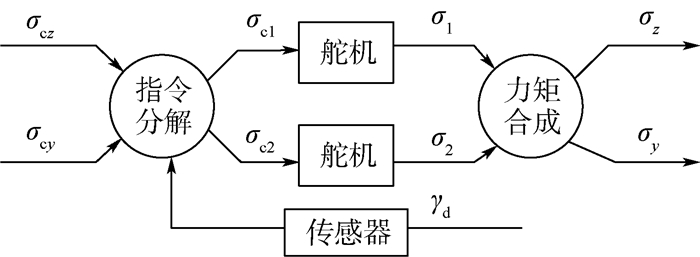
旋转弹在飞行过程中会受到外界干扰和不确定性的影响，并且存在气动交联、惯性交联和控制交联，为了实现稳定飞行，有必要进行解耦控制器设计。提出了一种基于滚动时域优化（RHO）的解耦控制方法。将旋转弹和舵机系统的动力学模型用状态空间形式描述，基于旋转弹、指令滤波器、积分跟踪误差的状态方程得到一个增广状态方程。采用基于指令滤波器的滚动时域优化方法进行控制量解算，根据系统输出与指令信号之间的差值实时调节控制器增益，实现旋转弹解耦控制。从加速度控制仿真结果可以看出，所设计的控制系统基本不受转速、建模误差和外界干扰的影响，具有较高的鲁棒性。
-
关键词:
- 旋转弹 /
- 解耦控制 /
- 滚动时域优化(RHO) /
- 加速度控制 /
- 指令滤波器
Abstract:The spinning missiles are subjected to external disturbances and uncertainties during flight, and there are the aerodynamic cross-linking, inertial cross-linking and control cross-linking. To realize stable flight, it is necessary to design decoupling controller. Therefore, a decoupling control method based on the receding horizon optimization (RHO) was proposed. The kinematic models of the spinning missile and the servo system were expressed in the form of state space, and the augmented equations of state were obtained based on the equations of state of the spinning missile, the command filters and the integral of the tracking error. The control value was calculated using the RHO based on the command filter, and in order to realize the decoupling control of the spinning missile, the controller gains were adjusted in real time according to the difference between the system output and the command signal. Through the acceleration control simulation results, it can be seen that the designed control system is basically not affected by the spinning rate, the modeling errors and the external disturbances, which has high robustness.
-
[1] 杨树兴, 赵良玉, 闫晓勇.旋转弹动态稳定性理论[M].北京:国防工业出版社, 2014:1-20.YANG S X, ZHAO L Y, YAN X Y.Dynamic stability theory of spinning projectile[M].Beijing:National Defence Industry Press, 2014:1-20(in Chinese). [2] 周伟. 旋转弹动态稳定性与鲁棒变增益控制[D]. 北京: 北京理工大学, 2016: 1-30.ZHOU W. Dynamic stability and robust variable gain control of spinning projectile[D]. Beijing: Beijing Institute of Technology, 2016: 1-30(in Chinese). [3] ZHOU W, YANG S X, DONG J L.Coning motion instability of spinning missiles induced by hinge moment[J].Aerospace Science and Technology, 2013, 30(1):239-245. doi: 10.1016/j.ast.2013.08.008 [4] 陈罗婧, 刘莉, 于剑桥.双通道控制旋转导弹自动驾驶仪解耦控制研究[J].北京理工大学学报, 2008, 28(1):11-14. http://www.nsfc.gov.cn/publish/portal0/tab434/info68686.htmCHEN L J, LIU L, YU J Q.Decoupling control of a double-channel control rolling missile autopilot[J].Transaction of Beijing Institute of Technology, 2008, 28(1):11-14(in Chinese). http://www.nsfc.gov.cn/publish/portal0/tab434/info68686.htm [5] 陈罗婧, 刘莉, 于剑桥.双通道控制旋转导弹自动驾驶仪回路数学变换及其耦合性分析[J].北京理工大学学报, 2007, 27(10):847-850. doi: 10.3969/j.issn.1001-0645.2007.10.001CHEN L J, LIU L, YU J Q.Transform and coupling analysis of double-channel control rolling missile autopilot loop[J].Transaction of Beijing Institute of Technology, 2007, 27(10):847-850(in Chinese). doi: 10.3969/j.issn.1001-0645.2007.10.001 [6] 袁天保, 刘新建, 秦子增.自旋弹弹导弹动力学与控制[J].宇航学报, 2006, 27(2):217-220. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yhxb200602015YUAN T B, LIU X J, QIN Z Z.Dynamic and control of spinning ballistic missile[J].Journal of Astronautics, 2006, 27(2):217-220(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yhxb200602015 [7] 闫晓勇, 李克勇, 杨树兴.基于动态逆理论的自旋弹控制方法[J].弹箭与制导学报, 2009, 29(5):83-86. http://www.cqvip.com/QK/97591A/200905/31996347.htmlYAN X Y, LI K Y, YANG S X.The control method of spinning missile based on dynamic inversion[J].Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(5):83-86(in Chinese). http://www.cqvip.com/QK/97591A/200905/31996347.html [8] THEODOULIS S, WERNERT P. Flight control for a class of 155 mm spin-stabilized projectiles with course correction fuse[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2011: 241-245. [9] THEODOULIS S, GASSMANN V, WERNERT P.Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J].Journal of Guidance, Control, and Dynamics, 2013, 36(2):517-531. doi: 10.2514/1.56520 [10] THEODOULIS S, SEVE F, WERNERT P.Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze[J].Aerospace Science and Technology, 2015, 42:477-489. doi: 10.1016/j.ast.2014.12.027 [11] WARD D G, BARRON R L. A self-designing receding horizon optimal flight controller[C]//Proceedings of the American Control Conference. Washington, D. C. : Barron Associates, 1995: 3490-3494. [12] FAWZY M, ABOELELA M A S, RHMAN O A E, et al.Design of missile control system using model predictive control[J].The Online Journal on Computer Science and Information Technology, 2011, 1(3):64-70. [13] BACHTIAR V. Multi-objective design of model predictive control and its application in missile autopilot and guidance[D]. Melbourne: University of Melbourne, 2016. [14] 钱杏芳, 林瑞雄, 赵亚男.导弹飞行力学[M].北京:北京理工大学出版社, 2006:60-70.QIAN X F, LIN R X, ZHAO Y N.Missile flight aerodynamics[M].Beijing:Beijing Institute of Technology Press, 2006:60-70(in Chinese). [15] SONNEVELDT L, CHU Q P, MULDER J A.Nonlinear flight control design using constrained adaptive backstepping[J].Journal of Guidance, Control, and Dynamics, 2007, 30(2):322-335. doi: 10.2514/1.25834 [16] 陈伟, 冯高鹏, 邓坤.基于滚动时域优化的变后掠角飞机修正控制律设计[J].南京航空航天大学学报, 2017, 49(1):96-104. http://www.cqvip.com/qk/92509XCHEN W, FENG G P, DENG K.Design of retrofit control law based on receding horizon optimal technique for variable sweep wing aircraft[J].Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(1):96-104(in Chinese). http://www.cqvip.com/qk/92509X [17] KIRK D E.Optimal control theory an introduction[M].New York:Dover Puchblications, 2004:90-93. [18] TODOROV E.Optimal control theory[M].Massachusetts:MIT Press, 2006:1-15. -
下载:
点击查看大图
计量
- 文章访问数: 764
- HTML全文浏览量: 219
- PDF下载量: 474
- 被引次数: 0
