基于八叉树的简化构型三角片等值面削减算法

徐雷; 王华锋; 潘海侠; 林广艳; 陈栎曦

doi:10.13700/j.bh.1001-5965.2017.0282

基于八叉树的简化构型三角片等值面削减算法

doi: 10.13700/j.bh.1001-5965.2017.0282

北京航空航天大学软件学院, 北京 100083

详细信息

作者简介:
徐雷男, 硕士研究生。主要研究方向:模式识别、机器学习

王华锋男, 博士, 副教授, 硕士生导师。主要研究方向:图像处理、模式识别、机器学习

通讯作者:
王华锋, E-mail: wanghuafeng@buaa.edu.cn

中图分类号: TP391
计量
- 文章访问数: 630
- HTML全文浏览量: 127
- PDF下载量: 462
- 被引次数: 0
出版历程
- 收稿日期: 2017-05-05
- 录用日期: 2017-09-01
- 网络出版日期: 2018-04-20

Octree based decimation algorithm for triangle isosurface using simplified patterns

School of Software, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

More Information

Corresponding author: WANG Huafeng, E-mail: wanghuafeng@buaa.edu.cn

摘要

摘要:
采用简化构型的SMC算法相比标准MC算法能够有效减少构成等值面的三角片的数量，但因为其仅是在体元内部的简化，所以不能较好地利用数据集表面局部形态特征。针对这一问题进一步提出OSMC算法。其根据简化构型的特点，首先采用八叉树结构组织体元，然后采用自底向上的合并策略合并节点，最后实现局部区域三角片合并。实验证明：OSMC算法能够实现比SMC算法更多的三角片削减，尤其对于具有较多平坦区域的数据集效果显著，其对公开数据集数据的平均削减率为55.1%，而SMC算法为29.7%，在面对高分辨率的地质数据时其最高削减率达到了80%，平均也超过了50%，同时OSMC算法能够更好地适应数据集分辨率的增长。
- 等值面 /
- MC算法 /
- SMC算法 /
- 八叉树 /
- 超体元
Abstract:
It is universally acknowledged that SMC based on simplified patterns extracts less triangles than the standard MC. Because only in-cube decimation was exploited, SMC is not able to take full advantage of local features of isosurfaces. Based on this observation, a new method named OSMC is presented in this paper. Based on characteristics of simplified configuration, OSMC first use octree structure to organize cells as nodes, then merge the nodes from bottom to top, and finally achieve local area triangles merging. The experimental results illustrate that the proposed method does further decimation than SMC, especially for datasets with large flat areas. The proposed method achieves an average reduction rate up to 55.1%, while the average reduction rate for SMC is 29.7%. The reduction rate reaches 80% at the highest and it is above 50% in average when OSMC is used on high-resolution geological dataset. Moreover, the new method is more adaptive to the increment of the dataset resolution.
- isosurface /
- MC algorithm /
- SMC algorithm /
- octree /
- super cell

HTML全文

图 1 MC算法构型

Figure 1. MC algorithm configuration

下载: 全尺寸图片幻灯片

图 2 SMC算法构型

Figure 2. SMC algorithm configuration

下载: 全尺寸图片幻灯片

图 3 OSMC算法流程

Figure 3. Flowchart of OSMC algorithm

下载: 全尺寸图片幻灯片

图 4 超体元提取三角片

Figure 4. Triangle extraction for super cell

下载: 全尺寸图片幻灯片

图 5 3种算法对Engine数据产生的表面全视图

Figure 5. Isosurface full view of three algorithms on Engine data set

下载: 全尺寸图片幻灯片

图 6 细节表面图

Figure 6. Detailed surface

下载: 全尺寸图片幻灯片

图 7 表面三角片构成情况

Figure 7. Composition of surface triangle

下载: 全尺寸图片幻灯片

图 8 3种算法人体肺部结节数据产生的网格和表面全视图

Figure 8. Mesh and isosurface full view of three algorithms on human pulmonary nodule data set

下载: 全尺寸图片幻灯片

图 9 3种算法人体肺部结节CT数据结果表面细节三角片构成情况

Figure 9. Triangles mesh part view of three algorithms on CT human pulmonary nodule data set

下载: 全尺寸图片幻灯片

图 10 3种算法对地质体数据产生的表面全视图

Figure 10. Isosurface full view of three algorithms on geological data set

下载: 全尺寸图片幻灯片

图 11 地质体数据集上平滑部分的三角片构成情况

Figure 11. Triangle mesh of flat area of geological data set

下载: 全尺寸图片幻灯片

图 12 地质体数据集上非平滑部分的三角片构成情况

Figure 12. Triangle mesh of uneven area of geological data set

下载: 全尺寸图片幻灯片

图 13 Table数据增长曲线

Figure 13. Table data growth curves

下载: 全尺寸图片幻灯片

图 14 四面体数据增长曲线

Figure 14. Tetrahedral data growth curves

下载: 全尺寸图片幻灯片

体元顶点与边

Number of vertices and edges of cell

下载: 全尺寸图片幻灯片

表 1 平面方程类型

Table 1. Types of plane equation

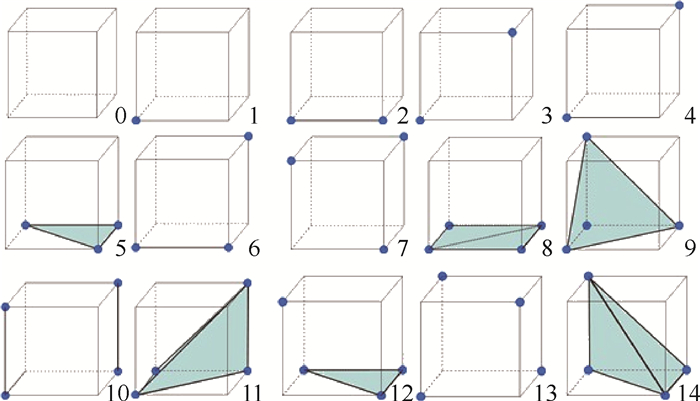
构型	三角片类型	平面方程类型
	正三角形	x+y+z=c
		x+y-z=c
		x-y-z=c
		x-y+z=c
	一般直角三角形	x+y=c
		x-y=c
		y+z=c
		y-z=c
		x+z=c
		x-z=c
	等腰直角三角形	x=c
		y=c
		z=c

下载: 导出CSV

表 2 部分数据集结果三角片数及削减率的对比

Table 2. Comparison between result of triangles numbers and reduction rate of part data set

数据集	三角片数			削减率/%
数据集	MC算法	SMC算法	OSMC算法	OSMC较SMC算法	OSMC较MC算法
Engine	622764	432370	259479	-40.0	-58.3
Fan	508928	370256	179179	-51.6	-64.8
Table	475548	439692	90073	-79.5	-81.1
Teapot	745152	508798	304008	-40.2	-59.2
Bonsai	644340	435994	372986	-14.5	-42.1
Skull	1842404	1114208	1033229	-7.3	-43.9
Backpack	3985836	2876044	2066527	-28.1	-48.2
Phantom	7457316	5296868	3557633	-32.8	-52.3
Lobster	1245556	721914	632738	-12.4	-49.2

下载: 导出CSV

表 3 人体肺部结节数据结果三角片数及削减率的对比

Table 3. Comparison between result of triangle numbers and reduction rate of human pulmonary nodules data set

数据集	三角片数			削减率/%
数据集	MC算法	SMC算法	OSMC算法	OSMC较SMC算法	OSMC较MC算法
肺部结节1	11652	7524	6498	-13.64	-44.23
肺部结节2	1992	1366	1160	-15.08	-41.77
肺部结节3	3704	2564	2012	-21.53	-45.68
肺部结节4	17360	10744	9198	-14.39	-47.02
肺部结节5	16212	10098	8623	-14.61	-46.81
肺部结节6	25052	16258	13583	-16.45	-45.78
肺部结节7	44344	25638	24213	-5.56	-45.40
肺部结节8	19972	11714	11350	-3.11	-43.17
总计				-10.80	-45.37

下载: 导出CSV

表 4 地质体数据结果三角片数及削减率的对比

Table 4. Comparison between result of triangle numbers and reduction rate of geological data set

数据集	三角片数			削减率/%
数据集	MC算法	SMC算法	OSMC算法	OSMC较SMC算法	OSMC较MC算法
地质体1	4216160	3068372	1569472	-48.85	-62.77
地质体2	3570748	3044366	1123834	-63.09	-68.53
地质体3	3998268	3018910	1068565	-64.60	-73.27
地质体4	7187412	5691550	1902811	-66.57	-73.53
地质体5	2374620	1788710	764733	-57.28	-67.80
地质体6	3348048	2714290	639024	-76.46	-80.91
地质体7	33408	26202	14492	-44.70	-56.62
总计				-63.40	-71.35

下载: 导出CSV

表 5 Table数据集4种分辨率下实验结果

Table 5. Results under four resolutions for Table data set

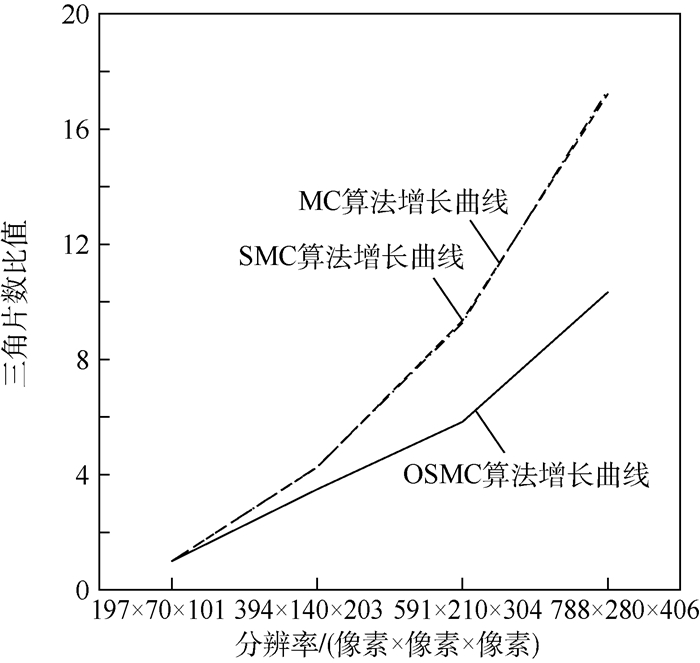
分辨率/(像素×像素×像素)	MC算法		SMC算法		OSMC算法
分辨率/(像素×像素×像素)	三角片数	与1倍分辨率比值	三角片数	与1倍分辨率比值	三角片数	与1倍分辨率比值
197×70×101	111652	1.00	103056	1.00	7028	1.00
394×140×203	475548	4.26	439692	4.27	10196	3.49
591×210×304	1045120	9.36	955408	9.27	17464	5.84
788×280×406	1920724	17.20	1786762	17.34	25334	10.33

下载: 导出CSV

表 6 四面体数据集4种分辨率下实验结果

Table 6. Experimental results under four resolutions for tetrahedral data set

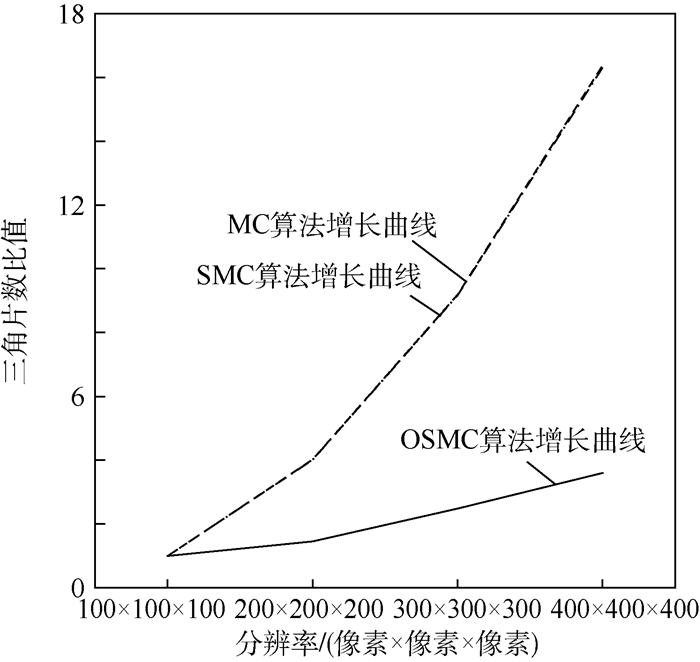
分辨率/(像素×像素×像素)	MC算法		SMC算法		OSMC算法
分辨率/(像素×像素×像素)	三角片数	与1倍分辨率比值	三角片数	与1倍分辨率比值	三角片数	与1倍分辨率比值
100×100×100	55868	1.00	37438	1.00	7028	1.00
200×200×200	224648	4.02	150152	4.01	10196	1.45
300×300×300	513332	9.19	343384	9.17	17464	2.48
400×400×400	914936	16.38	610738	16.31	25334	3.60

下载: 导出CSV

参考文献(24)

[1]	LORENSEN W E, CLINE H E. Marching cubes: A high resolution 3D surface construction algorithm[C]//ACM Siggraph Computer Graphics. New York: ACM, 1987, 21(4): 163-169.
[2]	HEIMBACH I, RHIEM F, BEULE F, et al.pyMolDyn:Identification, structure, and properties of cavities/vacancies in condensed matter and molecules[J].Journal of Computational Chemistry, 2017, 38(6):389-394. doi: 10.1002/jcc.24697
[3]	YIM P J, VASBINDER G B C, HO V B, et al.Isosurfaces as deformable models for magnetic resonance angiography[J].IEEE Transactions on Medical Imaging, 2003, 22(7):875-881. doi: 10.1109/TMI.2003.815056
[4]	BRONSON J R, SASTRY S P, LEVINE J A, et al.Adaptive and unstructured mesh cleaving[J].Procedia Engineering, 2014, 82:266-278. doi: 10.1016/j.proeng.2014.10.389
[5]	FERLEY E, CANI M P, GASCUEL J D.Practical volumetric sculpting[J].The Visual Computer, 2000, 16(8):469-480. doi: 10.1007/PL00007216
[6]	STEIN R, SHIH A M, BAKER M P, et al. Scientific visualization of water quality in the Chesapeake bay[C]//IEEE Visualization Conference. Piscataway, NJ: IEEE Press, 2000: 509-512.
[7]	TREMBILSKI A.Two methods for cloud visualisation from weather simulation data[J].The Visual Computer, 2001, 17(3):179-184. doi: 10.1007/PL00013405
[8]	KIM K, WITTENBRINK C M, PANG A. Data level comparison of surface classification and gradient filters[C]//Volume Graphics 2001. Berlin: Springer, 2001: 19-34.
[9]	NIELSON G M, HAMANN B. The asymptotic decider: Resolving the ambiguity in marching cubes[C]//Proceedings of the 2nd Conference on Visualization'91. Piscataway, NJ: IEEE Press, 1991: 83-91.
[10]	RECK F, DACHSBACHER C, GROSSO R, et al. Realtime iso-surface extraction with graphics hardware[C]//Eurographics. Geneva: Eurographics, 2004: 1-4.
[11]	JOHANSSON G, CARR H. Accelerating marching cubes with graphics hardware[C]//Proceedings of the 2006 Conference of the Center for Advanced Studies on Collaborative Research. Armonk: IBM Corporation, 2006, 6: 39.
[12]	NEWMAN T S, YI H.A survey of the marching cubes algorithm[J].Computers & Graphics, 2006, 30(5):854-879. http://cn.bing.com/academic/profile?id=35d7de94390ab0a2b543fb539cacded5&encoded=0&v=paper_preview&mkt=zh-cn
[13]	SCHROEDER W J, ZARGE J A, LORENSEN W E. Decimation of triangle meshes[C]//ACM Siggraph Computer Graphics. New York: ACM, 1992, 26(2): 65-70.
[14]	GARLAND M, HECKBERT P S. Surface simplification using quadric error metrics[C]//Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press/Addison-Wesley Publishing Co., 1997: 209-216.
[15]	MONTANI C, SCATENI R, SCOPIGNO R. Discretized marching cubes[C]//Proceedings of the Conference on Visualization'94. Piscataway, NJ: IEEE Press, 1994: 281-287.
[16]	MONTANI C, SCATENI R, SCOPIGNO R.Decreasing isosurface complexity via discrete fitting[J].Computer Aided Geometric Design, 2000, 17(3):207-232. http://dl.acm.org/citation.cfm?id=868953
[17]	SHU R, ZHOU C, KANKANHALLI M S.Adaptive marching cubes[J].The Visual Computer, 1995, 11(4):202-217. doi: 10.1007/BF01901516
[18]	SHEKHAR R, FAYYAD E, YAGEL R, et al. Octree-based decimation of marching cubes surfaces[C]//7th Annual IEEE Conference on Visualization. Piscataway, NJ: IEEE Press, 1996: 335-342.
[19]	OHTAKE Y, BELYAEV A, ALEXA M, et al. Multi-level partition of unity implicits[C]//ACM Siggraph 2005 Courses. New York: ACM, 2005: 173.
[20]	KAZHDAN M, HOPPE H.Screened poisson surface reconstruction[J].ACM Transactions on Graphics (TOG), 2013, 32(3):29. http://www.cs.jhu.edu/~misha/Code/PoissonRecon/Version8.0
[21]	WILHELMS J, VAN GELDER A.Octrees for faster isosurface generation[J].ACM Transactions on Graphics (TOG), 1992, 11(3):201-227. doi: 10.1145/130881.130882
[22]	WESTERMANN R, KOBBELT L, ERTL T.Real-time exploration of regular volume data by adaptive reconstruction of isosurfaces[J].The Visual Computer, 1999, 15(2):100-111. http://cn.bing.com/academic/profile?id=6e397049916ce26c3253dedc5cd0b83e&encoded=0&v=paper_preview&mkt=zh-cn
[23]	CUI S H, LIU J.Simplified patterns for extracting the isosurfaces of solid objects[J].Image and Vision Computing, 2008, 26(2):174-186. doi: 10.1016/j.imavis.2007.02.003
[24]	VIGNOLES G L, DONIAS M, MULAT C, et al.Simplified marching cubes:An efficient discretization scheme for simulations of deposition/ablation in complex media[J].Computational Materials Science, 2011, 50(3):893-902. doi: 10.1016/j.commatsci.2010.10.027