-
摘要:
现有的不确定性模型确认方法建立在概率理论基础之上，仅仅适用于随机不确定性因素影响下的模型确认，而不适合随机和区间变量共存条件下的模型确认问题。针对这一问题，研究了随机和区间变量共存条件下的模型确认方法。首先，分析了随机和区间变量共存条件下数学模型的特点；然后，运用概率方法和区间理论，提出了一种新的模型确认指标，通过模型响应量的上下界分布函数（CDF）与实验响应量的上下界经验CDF之间差异，来度量随机和区间输入变量共存条件下模型预测与实际物理实验结果之间的不一致性；讨论了所提指标的数学性质，给出了指标的计算方法和步骤；最后，采用一个数字算例和一个工程算例验证了所提指标在随机和区间输入变量共存条件下进行模型确认的可行性和有效性。
Abstract:The existing model validation methods under uncertainty based on theory of probability are only applicable to validate model with random variables, but inapplicable to validate model with the mixture of random and interval variables. To address this issue, the validation method for model with the mixture of random and interval variables is studied in this paper. First, the characteristics of the mathematical model with the mixture of random and interval variables are analyzed. Second, a new validation metric is proposed by using interval theory and probability method. This metric provides a comparison between the cumulative distribution functions (CDFs) of the upper and the lower bounds of the model responses and the empirical CDFs of the upper and the lower bounds of the experimental responses to show the disagreement between the quantitative predictions from a model and the physical observations. The mathematical properties of the new metric are discussed, and its estimation method and procedures are presented. Finally, the feasibility and effectiveness of the proposed validation metric are illustrated by a numerical test case and an engineering application with mixture of random and interval variables.
-
Key words:
- model validation /
- metric /
- random variables /
- interval variables /
- mixed model
-
图 2 模型和实验响应量上下界分布函数和经验分布函数
Figure 2. CDFs and empirical CDFs of upper and lower bounds of model and experimental responses
图 3 航空发动机涡轮盘模型裂纹示意图
Figure 3. Schematic diagram of crack of an aero engine turbo blade model
表 1 2组测试计算模型
Table 1. Computation models in two test cases
测试组 模型编号 模型公式 第1组 1 ym1(x)=ye(x, θ=1.5) 2 ym2(x)=ye(x, θ=1.6) 3 ym2(x)=ye(x, θ=1.7) 第2组 4 ym4(x)=ye(x, θ~N(1.5, 0.152)) 5 ym5(x)=ye(x, θ~N(1.5, 0.32)) 6 ym6(x)=ye(x, θ~N(1.6, 0.32)) 注：ymi(x)(i=1, 2, …, 6)表示第i个模型的输出响应量。 
下载: 导出CSV
表 2 数字算例的指标计算结果
Table 2. Metric computation results of numerical test case
测试组 模型编号 指标值 第1组 1 0.007 6 2 0.155 1 3 0.332 0 第2组 4 0.050 2 5 0.163 5 6 0.276 7
下载: 导出CSV
表 3 发动机涡轮盘输入变量分布参数
Table 3. Distribution parameters of input variables of engine turbo blade
随机变量 分布类型 均值 变异系数 ρ 对数正态 8 240 0.1 C 对数正态 5.67 0.1 J 正态 1.22×10-4 0.1
下载: 导出CSV
表 4 航空发动机涡轮盘模型输入变量分布参数
Table 4. Distribution parameters of input variables of models of aero engine turbo blade
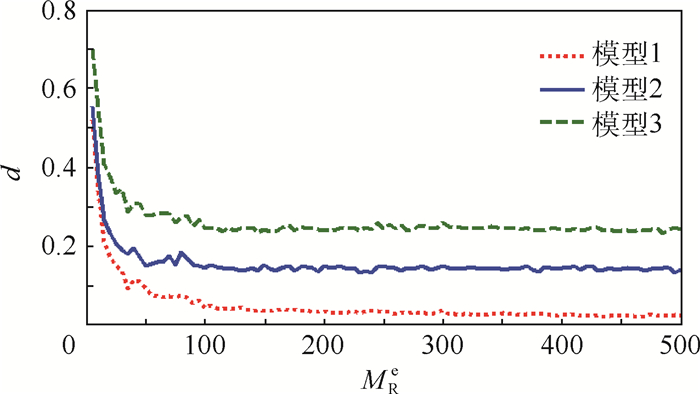
随机变量 分布类型 模型1 模型2 模型3 均值 变异系数 均值 变异系数 均值 变异系数 ρ 对数正态 8 240 0.1 8 240 0.15 8 240 0.15 C 对数正态 5.67 0.1 5.67 0.15 5.67 0.15 J 正态 1.22×10-4 0.1 1.22×10-4 0.15 1.31×10-4 0.15
下载: 导出CSV
表 5 航空发动机涡轮盘模型确认指标计算结果
Table 5. Model validation metric computation results of aero engine turbo blade
模型 模型1 模型2 模型3 指标值 0.012 3 0.136 9 0.239 6
下载: 导出CSV
-
[1] OBERKAMPF W L, ROY C J.Verification and validation in scientific computing[M].New York:Cambridge University Press, 2010:21-25. [2] OBERKAMPF W L, BARONE M F.Measures of agreement between computation and experiment:Validation metrics[J].Journal of Computational Physics, 2006, 217:5-36. doi: 10.1016/j.jcp.2006.03.037 [3] OBERKAMPF W L, SINDIR M, CONLISK A.Guide for the verification and validation of computational fluid dynamics simulations[M].Reston:AIAA, 1998:2-4. [4] XIONG Y, CHEN W, TSUI K L, et al.A better understanding of model updating strategies in validating engineering models[J].Compute Methods in Applied Mechanics and Engineering, 2009, 189(15-16):1327-1337. [5] MESSER M, PANCHAL J H, KRISHNAMURTHY V, et al.Model selection under limited information using a value of information based indicator[J].Journal of Mechanical Design, 2010, 132(12):121008. doi: 10.1115/1.4002751 [6] KENNEDY M C, O'HAGAN A.Bayesian calibration of computer models[J].Journal of the Royal Statistical Society, 2001, 63(3):425-464. doi: 10.1111/rssb.2001.63.issue-3 [7] BAYARRI M J, BERGER J O, PAULO R, et al.A framework for validation of computer models[J].Technometrics, 2007, 49(2):138-154. doi: 10.1198/004017007000000092 [8] ARENDT P D, APLEY D W, CHEN W, et al.Improving identifiability in model calibration using multiple responses[J].Journal of Mechanical Design, 2012, 134(10):100909. doi: 10.1115/1.4007573 [9] ARENDT P D, APLEY D W, CHEN W.Quantification of model uncertainty:Calibration, model discrepancy, and identifiability[J].Journal of Mechanical Design, 2012, 134(10):100908. doi: 10.1115/1.4007390 [10] LIU Y, CHEN W, ARENDT P, et al.Toward a better understanding of model validation metrics[J].Journal of Mechanical Design, 2011, 133(7):071005. doi: 10.1115/1.4004223 [11] REBBA R, MAHADEVAN S.Validation of models with multivariate output[J].Reliability Engineering and System Safety, 2006, 91(8):861-871. doi: 10.1016/j.ress.2005.09.004 [12] FERSON S, OBERKAMPF W L.Validation of imprecise probability models[J].International Journal of Reliability and Safety, 2009, 3:3-22. doi: 10.1504/IJRS.2009.026832 [13] FERSON S, OBERKAMPF W L, GINZBURG L.Model validation and predictive capability for the thermal challenge problem[J].Computer Methods in Applied Mechanics and Engineering, 2008, 197(29-32):2408-2430. doi: 10.1016/j.cma.2007.07.030 [14] 赵录峰, 吕震宙, 张磊刚, 等.多输出模型确认中的混合矩指标[J].国防科技大学学报, 2015, 37(6):61-68. doi: 10.11887/j.cn.201506013ZHAO L F, LYU Z Z, ZHANG L G, et al.Mixed moment validation metric for models with multivariate output[J].Journal of National University of Defense Technology, 2015, 37(6):61-68(in Chinese). doi: 10.11887/j.cn.201506013 [15] LI W, CHEN W, JIANG Z, et al.New validation metrics for models with multiple correlated responses[J].Reliability Engineering and System Safety, 2014, 127:1-11. doi: 10.1016/j.ress.2014.02.002 [16] ZHAO L F, LU Z Z, YUN W Y, et al.Validation metric based on Mahalanobis distance for models with multiple correlated responses[J].Reliability Engineering and System Safety, 2017, 159:80-89. doi: 10.1016/j.ress.2016.10.016 [17] 胡嘉蕊, 吕震宙.基于核主成分分析的多输出模型确认方法[J].北京航空航天大学学报, 2017, 43(7):1470-1480. http://bhxb.buaa.edu.cn/CN/abstract/abstract14108.shtmlHU J R, LYU Z Z.Model validation model with multivariate output based on kernel principal component analysis[J].Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7):1470-1480(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract14108.shtml -
下载:
点击查看大图
计量
- 文章访问数: 782
- HTML全文浏览量: 55
- PDF下载量: 326
- 被引次数: 0
