采用FRM的窄过渡带奇型排列结构改进方法

张文旭; 赵文童; 陈涛; 陈亚静

doi:10.13700/j.bh.1001-5965.2017.0365

采用FRM的窄过渡带奇型排列结构改进方法

doi: 10.13700/j.bh.1001-5965.2017.0365

哈尔滨工程大学信息与通信工程学院, 哈尔滨 150001

基金项目:

国家自然科学基金 61571146

详细信息

作者简介:
张文旭男, 博士, 讲师。主要研究方向:宽带信号检测、处理与识别

赵文童男, 硕士研究生。主要研究方向:数字信道化技术

陈涛男, 博士, 教授, 博士生导师。主要研究方向:宽带信号检测、处理与识别

陈亚静女, 硕士。主要研究方向:数字信道化技术

通讯作者:
张文旭, E-mail: zhangwenxu@hrbeu.edu.cn

中图分类号: TN971.⁺1
计量
- 文章访问数: 938
- HTML全文浏览量: 209
- PDF下载量: 423
- 被引次数: 0
出版历程
- 收稿日期: 2017-05-31
- 录用日期: 2017-11-23
- 网络出版日期: 2018-05-20

An improved approach for odd-arrangement structure with narrow transition band based on FRM

College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China

Funds:

National Natural Science Foundation of China 61571146

More Information

Corresponding author: ZHANG Wenxu, E-mail:zhangwenxu@hrbeu.edu.cn

摘要

摘要:
为了解决数字信道化中窄过渡带滤波器组计算复杂度较高的问题，提出了一种采用频率响应屏蔽（FRM）的窄过渡带奇型排列非最大抽取滤波器组高效结构。在设计该结构的原型滤波器时，首先通过对原型滤波器进行插值得到FRM上支路的滤波器，然后将信号延时与插值后的滤波器相减得到位于下支路的互补滤波器，再利用屏蔽滤波器对插值产生的多余镜像进行屏蔽，最终得到所设计的FRM滤波器。对该改进结构进行了MATLAB仿真，仿真结果验证了该改进结构的正确性。与多相滤波器组结构相比，采用该结构可节省约80%的乘法器资源。由于该改进结构中将抽取提前，降低了系统采样率的限制条件，可以直接应用于高速采样系统中。
- 窄过渡带 /
- 原型滤波器 /
- 频率响应屏蔽(FRM) /
- 滤波器组 /
- 屏蔽滤波器
Abstract:
In order to solve the problem of high computation complexity of narrow transition band filter bank, an odd-arrangement non-maximally decimated efficient structure with narrow transition band filter bank based on frequency response masking (FRM) is proposed. Firstly, when the prototype filter of this structure is designed, the FRM filter of the upper arm is obtained through the interpolated prototype filter. Secondly, the complementary filter of the lower arm is obtained by the delay signal subtracted from the interpolated prototype filter. Then the masking filter is used to shield the mirror caused by the interpolated filter. Finally, the desired FRM filter is obtained. The improved structure is simulated by MATLAB, and the simulation results verify the correctness of this improved structure. This efficient structure saves 80% of the multiplier resources compared with the polyphase filter bank architecture. Because the decimation module is located at the front of this improved structure, the limited condition of the sampling rate of the system is reduced and it can be directly used in the high-speed sampling system.
- narrow transition band /
- prototype filter /
- frequency response masking (FRM) /
- filter bank /
- masking filter

HTML全文

图 1 FRM滤波器的基本框架

Figure 1. Basic framework of FRM filter

下载: 全尺寸图片幻灯片

图 2 滤波器插值过程(L=4)

Figure 2. Process of filter interpolation for L=4

下载: 全尺寸图片幻灯片

图 3 采用FRM技术设计低通滤波器^{[12, 16]}

Figure 3. Design of low-pass filter based on FRM^{[12, 16]}

下载: 全尺寸图片幻灯片

图 4 滤波器组频带划分

Figure 4. Band division of filter bank

下载: 全尺寸图片幻灯片

图 5 滤波器组低通实现结构

Figure 5. Low-pass structure of filter bank

下载: 全尺寸图片幻灯片

图 6 滤波器组信道化高效结构

Figure 6. Efficient channelization structure of filter bank

下载: 全尺寸图片幻灯片

图 7 FRM滤波器的频率响应合成过程

Figure 7. Frequency response synthesis process of FRM filter

下载: 全尺寸图片幻灯片

图 8 采用FRM的窄过渡带奇型排列高效结构

Figure 8. Odd-arrangement efficient structure with narrow transition band based on FRM

下载: 全尺寸图片幻灯片

图 9 原型滤波器幅频响应

Figure 9. Amplitude-frequency response of prototype filter

下载: 全尺寸图片幻灯片

图 10 原型屏蔽滤波器幅频响应

Figure 10. Amplitude-frequency response of prototype masking filter

下载: 全尺寸图片幻灯片

图 11 FRM滤波器幅频响应

Figure 11. Amplitude-frequency response of FRM filter

下载: 全尺寸图片幻灯片

图 12 FRM滤波器组幅频响应

Figure 12. Amplitude-frequency response of FRM filter bank

下载: 全尺寸图片幻灯片

图 13 FRM滤波器组输出频域波形

Figure 13. Output frequency domain waveform of FRM filter bank

下载: 全尺寸图片幻灯片

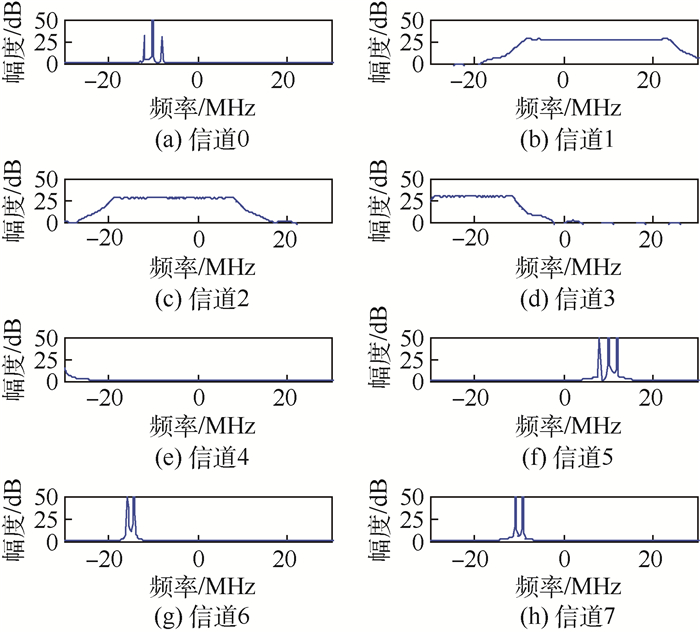
表 1 输入信号参数设置

Table 1. Parameter setting of input signals

输入信号	载波频率/MHz	调制频率/MHz	理论输出信道编号
LFM1	70	-10~+10	3、4
AM1	140	1	5
LFM2	205	-15~+15	2
DSB1	285	0.7	6
LFM3	339	-19~+19	1
DSB2	400	0.8	7
AM2	440	2	0

下载: 导出CSV

参考文献(16)

[1]	HARRIS F J, DICK C, RICE M.Digital receivers and transmi-tters using polyphase filter banks for wireless communication[J].IEEE Transactions on Microwave Theory and Techniques, 2003, 51(4):1395-1412. doi: 10.1109/TMTT.2003.809176
[2]	BARROS A K, RUTKOWSKI T, LTAKURA F.Estimation of speech embedded in a reverberant and noisy environment by independent component analysis and wavelets[J].IEEE Transactions on Neural Networks, 2002, 13(4):888-893. doi: 10.1109/TNN.2002.1021889
[3]	DO M N, VETTERLI M.The contourlet transform:An efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing, 2005, 14(12):2091-2106. doi: 10.1109/TIP.2005.859376
[4]	HONG Y, LIAN Y. Continuous-time FIR filters based on frequency-response masking technique[C]//2015 IEEE International Conference on Digital Signal Processing. Piscataway, NJ: IEEE Press, 2015: 191-195.
[5]	ROMERO D E T. High-speed multiplierless frequency response masking(FRM) FIR filters with reduced usage of hardware resources[C]//2015 IEEE 58th International Midwest Symposium on Circuits and Systems. Piscataway, NJ: IEEE Press, 2015: 1-4.
[6]	LU W, HINAMOTO T.A unified approach to the design of interpolated and frequency-response-masking FIR filters[J].IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2016, 63(12):2257-2266. doi: 10.1109/TCSI.2016.2613880
[7]	WEI Y, HUANG S G, MA X J.A novel approach to design low-cost two-stage frequency response masking filters[J].IEEE Transactions on Circuits and Systems, 2015, 62(10):982-986.
[8]	SHEN T, LIM Y C. Low complexity frequency-response masking filters using modified structure based on serial masking[C]//19th European Signal Processing Conference. Kessariani: EURASIP, 2011: 1400-1404.
[9]	陈涛, 王莹, 刘勇.基于频率响应屏蔽的窄过渡带信道化接收机[J].吉林大学学报, 2015, 45(1):335-340. http://www.oalib.com/paper/4824859 CHEN T, WANG Y, LIU Y.Digital channelized receiver with narrow transiton band based on FRM filter[J].Journal of Jilin University, 2015, 45(1):335-340(in Chinese). http://www.oalib.com/paper/4824859
[10]	LI N, NOWROUZIAN B. Application of frequency-response masking technique to the design of a novel modified-DFT filter banks[C]//IEEE ISCAS, 2006: 3293-3296.
[11]	KUMAR A, SUNKARIA R K. Design of prototype filter using windowing and linear optimization technique for the non-uniform filter banks[C]//2013 International Conference on Recent Trends in Information Technology. Piscataway, NJ: IEEE Press, 2014: 352-358.
[12]	SUMEDH D, SMITHA K G, VINOD A P. A low complexity reconfigurable channel filter based on decimation, interpolation and frequency response masking[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ: IEEE Press, 2013: 5583-5587.
[13]	张文旭, 陈亚静, 陈涛, 等.基于FRM的偶型排列信道化改进结构[J].北京邮电大学学报, 2016, 39(3):27-33. http://cdmd.cnki.com.cn/Article/CDMD-10217-1011021324.htm ZHANG W X, CHEN Y J, CHEN T, et al.Improved structure of even-arrangement channelized based on FRM[J].Journal of Beijing University of Posts and Telecommunications, 2016, 39(3):27-33(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10217-1011021324.htm
[14]	TSUI K M, CHAN S C, LIM Y C.Design of multiplet perfect reconstruction filter banks using frequency response masking technique[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2008, 55(9):2707-2715. doi: 10.1109/TCSI.2008.920086
[15]	BINDIYA T S, ELIAS E.Metaheuristic algorithms for the design of multiplier-less non-uniform filter banks based on frequency response masking[J].Soft Computing, 2014, 18(8):1529-1547. doi: 10.1007/s00500-013-1158-8
[16]	DHABU S, VINOD A P.Design and FPGA implementation of reconfigurable linear phase digital filter with wide cutoff frequency range and narrow transition bandwidth[J].IEEE Tran-sactions on Circuits and Systems Ⅱ:Express Briefs, 2016, 63(2):181-185. doi: 10.1109/TCSII.2015.2483418