基于形态学的自动驾驶仪振动信号基线漂移去噪

张景元; 何玉珠

doi:10.13700/j.bh.1001-5965.2017.0371

基于形态学的自动驾驶仪振动信号基线漂移去噪

doi: 10.13700/j.bh.1001-5965.2017.0371

张景元,
何玉珠^,

北京航空航天大学仪器科学与光电工程学院, 北京 100083

详细信息

作者简介:
张景元男, 硕士研究生。主要研究方向:自动测试技术与故障诊断

何玉珠男, 博士, 教授。主要研究方向:测试系统通用性技术、故障诊断、定位技术

通讯作者:
何玉珠, E-mail: heyuzhuhe@buaa.edu.cn

中图分类号: TP391
计量
- 文章访问数: 648
- HTML全文浏览量: 70
- PDF下载量: 452
- 被引次数: 0
出版历程
- 收稿日期: 2017-06-05
- 录用日期: 2017-08-01
- 网络出版日期: 2018-05-20

Removing baseline drift in vibration signal of autopilot based on morphology

ZHANG Jingyuan,
HE Yuzhu^,

School of Instrumentation Science and Opto-electronics Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

More Information

Corresponding author: HE Yuzhu, E-mail: heyuzhuhe@buaa.edu.cn

摘要

摘要:
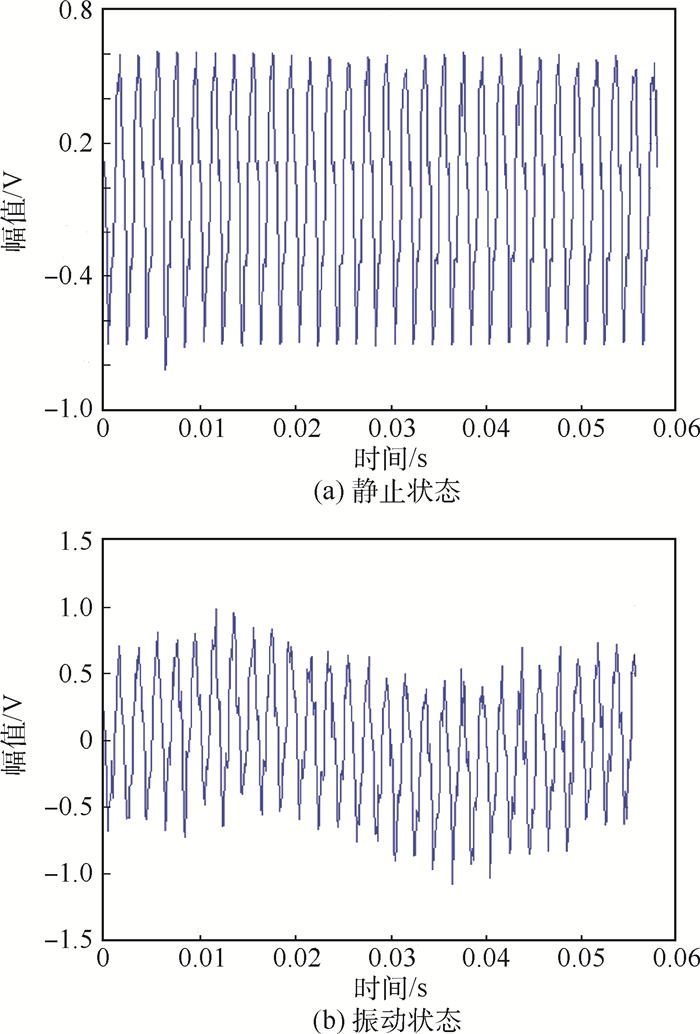
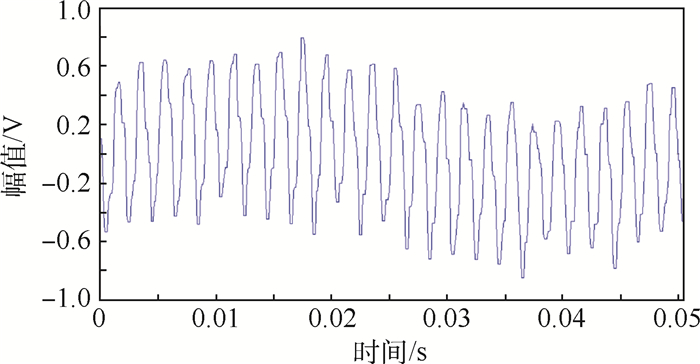
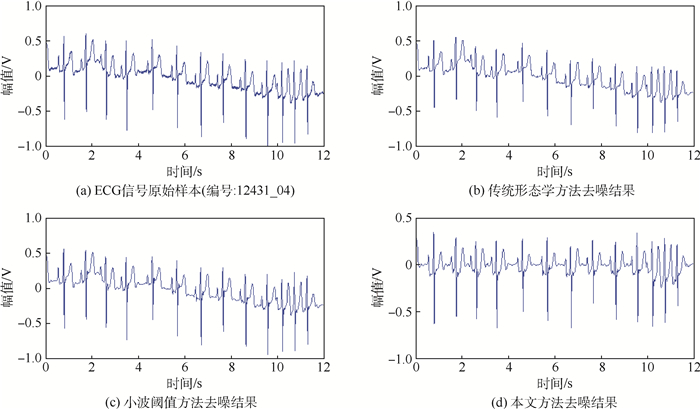
导弹自动驾驶仪在振动测试过程中存在信号基线漂移且污染严重的问题，而传统的时频处理方法难以达到去噪要求，因此基于形态学基本原理提出了一种用于解决振动信号基线漂移的滤波方法。该滤波方法由3级结构组成，前2级结构均是基于形态学基本原理，第3级进行相消与平滑处理，通过相互级联，可以有效抑制基线漂移。此外，通过引入粒子群优化（PSO）算法使得该滤波方法更具适应性。对比实验利用该滤波方法和对比方法对自动驾驶仪实测振动信号与标准ECG信号进行了处理，结果表明：该滤波方法在抑制基线漂移方面要优于小波阈值去噪和传统的形态学去噪。
- 形态学滤波 /
- 振动信号 /
- 基线漂移 /
- 阈值去噪 /
- 粒子群优化(PSO)
Abstract:
The baseline drift and heavy pollution for vibration test of missile autopilot are still problems. The requirement of denoising is difficult to be achieved by traditional time-frequency method. In this paper, to filter out the baseline drift noise, a new morphological filtering method based on the basic principle of generalized morphology is proposed. The proposed method is composed of three-level structure:the former two are based on the morphological principle, and the third level is designed for cancellation and smoothing. Thus, baseline drift can be effectively suppressed by cascading. In addition, the proposed method is more adaptive by introducing particle swarm optimization (PSO). In the final experiments, the real signals of autopilot and ECG signals are denoised by the proposed method and reference methods. The experimental results show that the proposed method is better than wavelet denoising and traditional morphological denoising in suppressing baseline drift.
- morphological filtering /
- vibration signal /
- baseline drift /
- threshold denoising /
- particle swarm optimization (PSO)

HTML全文

图 1 级联滤波器结构模型

Figure 1. Structure model of cascading filter

下载: 全尺寸图片幻灯片

图 2 直线形结构元素基本模型

Figure 2. Basic model of linear structural elements

下载: 全尺寸图片幻灯片

图 3 静止和振动状态实测信号

Figure 3. Measured signals in static and vibration states

下载: 全尺寸图片幻灯片

图 4 传统形态学方法去噪结果

Figure 4. Denoising results of traditional morphological method

下载: 全尺寸图片幻灯片

图 5 小波阈值方法去噪结果

Figure 5. Denoising results of wavelet threshold method

下载: 全尺寸图片幻灯片

图 6 L和θ对去噪效果的影响

Figure 6. Influence of L and θ on denoising

下载: 全尺寸图片幻灯片

图 7 本文方法对自动驾驶仪实测振动信号的去噪结果

Figure 7. Denoising results of measured vibration signal of autopilot using proposed method

下载: 全尺寸图片幻灯片

图 8 本文方法和对比方法对B型号导弹自动驾驶仪实测振动信号的去噪结果

Figure 8. Denoising results of measured vibration signal of Type B missile autopilot by proposed method and reference method

下载: 全尺寸图片幻灯片

图 9 含有基线漂移噪声的ECG信号去噪结果

Figure 9. Denoising results of ECG signals containing baseline drift noise

下载: 全尺寸图片幻灯片

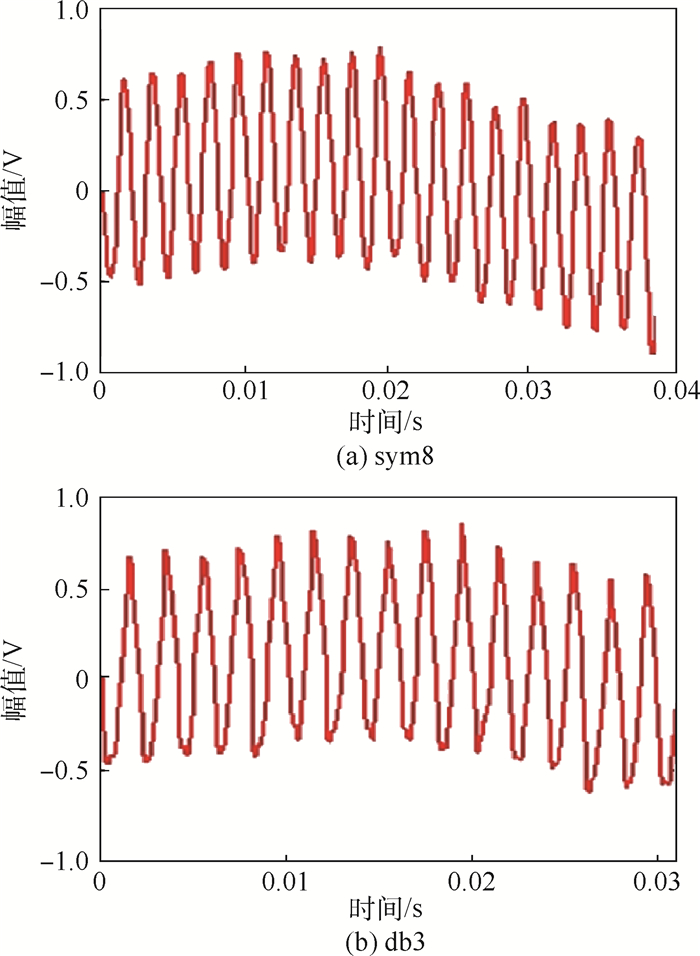
表 1 不同分解层数下小波阈值去噪结果

Table 1. Denoising results of wavelet transformation with different wavelet-bases

小波基	分解层数	均方差	信噪比	波形相似比
sym8	2	0.151	20.80	0.94
sym8	3	0.202	13.82	0.89
sym8	4	0.428	-21.84	0.32
db3	2	0.165	18.71	0.93
db3	3	0.254	7.76	0.83
db3	4	0.428	-21.42	0.32

下载: 导出CSV

表 2 PSO算法优化结果

Table 2. Optimization results using PSO algorithm

实验次数	L₁	θ₁	L₂	θ₂	信噪比
1	2	2	29	40	28.7
2	3	3	30	80	28.7
3	3	2	78	72	28.7
4	3	5	68	65	27.6
5	3	5	76	40	27.6
6	2	3	36	72	28.1

下载: 导出CSV

参考文献(18)

[1]	EVANS J W, KUNDU P, HOROVITZ S G, et al. Separating slow BOLD from non-BOLD baseline drifts using multi-echo FMRI[J].NeuroImage, 2015, 105:189-197. doi: 10.1016/j.neuroimage.2014.10.051
[2]	CHIU H C.Stable baseline correction of digital strong-motion data[J].Bulletin of Seismological Society of America, 1997, 87(4):932-944. http://ci.nii.ac.jp/naid/10011629579
[3]	BOORE D M, BOMMER J J.Processing of strong-motion accelerograms:Needs, options and consequences[J].Soil Dynamics and Earthquake Engineering, 2005, 25(2):93-115. doi: 10.1016/j.soildyn.2004.10.007
[4]	PAN C, ZHANG R F, LUO H, et al.Baseline correction of vibration acceleration signals with inconsistent initial velocity and displacement[J].Advances in Mechanical Engineering, 2016, 8(10):1-11. https://www.researchgate.net/publication/309361346_Baseline_correction_of_vibration_acceleration_signals_with_inconsistent_initial_velocity_and_displacement
[5]	MORITA S, KITAGAWA K.Effect of baseline drift on perturbat-correlation moving-window two-dimensional correlation spectroscopy[J].Vibrational Spectroscopy, 2012, 60:217-219. doi: 10.1016/j.vibspec.2011.10.003
[6]	WANG Y, JI Y J, LI S Y.A wavelet-based baseline drift correction method for grounded electrical source airborne transient electromagnetic signals[J].Exploration Geophysics, 2013, 44(4):229-237. doi: 10.1071/EG12078
[7]	邓璐, 庞宇, 赵艳霞, 等.基于形态学的心电信号基线漂移矫正方法[J].数字通信, 2013, 40(3):14-16. http://mall.cnki.net/magazine/Article/SZTX201303009.htm DENG L, PANG Y, ZHAO Y X, et al.Removal method of baseline drift from ECG signals based on morphology filter[J].Digital Communication, 2013, 40(3):14-16(in Chinese). http://mall.cnki.net/magazine/Article/SZTX201303009.htm
[8]	LUO Y R, HARGRAVES R H, BELLE A, et al.A hierarchical method for removal of baseline drift from biomedical signals:Application in ECG analysis[J].Scientific World Journal, 2013, 2013:896056. https://www.researchgate.net/profile/Kayvan_Najarian/publication/237843506_A_Hierarchical_Method_for_Removal_of_Baseline_Drift_from_Biomedical_Signals_Application_in_ECG_Analysis/links/0f317534be911a0b8d000000.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail
[9]	DU Y G, CHAMBERS S A.Etalon-induced baseline drift and correction in atom flux sensors based on atomic absorption spectroscopy[J].Applied Physics Letters, 2014, 105(16):163113. doi: 10.1063/1.4898638
[10]	LOPATKA M, BARCARU A, SJERPS M J, et al.Leveraging probabilistic peak detection to estimate baseline drift in complex chromatographic samples[J].Journal of Chromatography A, 2016, 1431:122-130. doi: 10.1016/j.chroma.2015.12.063
[11]	LIU G F, LUO X L, YANG J.Baseline drift effect on the performance of neutron and γ ray discrimination using frequency gradient analysis[J].Chinese Physics C, 2013, 37(6):63-69. https://arxiv.org/pdf/1305.1718
[12]	ZHU F, QIN B J, FENG W Y, et al.Reducing Poisson noise and baseline drift in x-ray spectral images with bootstrap Poisson regression and robust nonparametric regression[J].Physics in Medicine and Biology, 2013, 58(6):1739-1758. doi: 10.1088/0031-9155/58/6/1739
[13]	WANG R Q, LI Q, ZHANG M.Application of multi-scaled morphology in denoising seismic data[J].Applied Geophyiscs, 2008, 5(3):197-203. doi: 10.1007/s11770-008-0033-3
[14]	SALEMBIER P, WILKINSON M H F.Connected operators:A review of region-based morphological image processing techniques[J].IEEE Signal Processing Magazine, 2009, 26(6):136-157. doi: 10.1109/MSP.2009.934154
[15]	赵于前, 王小芳, 李桂源.基于多尺度多结构元素的肝脏图像分割[J].光电子·激光, 2009, 20(4):563-566. http://www.cqvip.com/QK/92586A/200904/1000623334.html ZHAO Y Q, WANG X F, LI G Y.Liver image segmentation based on multi-scale and multi-structure elements[J].Journal of Optoelectronics·Laser, 2009, 20(4):563-566(in Chinese). http://www.cqvip.com/QK/92586A/200904/1000623334.html
[16]	GAUTAM S, BRAHMA S M. Overview of mathematical morphology in power systems-A tutorial approach[C]//2009 IEEE Power & Energy Society General Meeting. Piscataway, NJ: IEEE Press, 2009: 3523-3529.
[17]	KOZUMPLÍK J, PROVAZNÍK I.Fast timevarying linear flters for suppression of baseline drift in electrocardiographic signals[J].Biomedical Engineering Online, 2017, 16:24. doi: 10.1186/s12938-017-0316-0
[18]	SERRA J.Image analysis and mathematical morphology[M].New York:Academic Press, 1982.