Differential evolution optimization for stuffed Whipple shield ballistic limit equations
-
摘要:
综合建模形式弹道极限方程中存在11个待定参数,从理论上讲,采用穷举法可以获得其数值大小,但需要的计算时间过长,储存空间巨大,不宜实现,为解决此问题,改用差异演化算法。基于填充式实验数据,采用差异演化算法对综合建模形式弹道极限方程的11个待定参数进行了多目标优化计算。结果显示,方程的总体预测率为82.35%,安全预测率为100%,平均相对误差平方和为0.001 3。该方程对其他来源的49个实验数据的预测结果显示,总体预测率提升了1.32%,安全预测率降低了4.08%,平均相对误差平方和增加了0.007 3,表明差异演化算法适用于解决多参数多目标的弹道极限方程建模问题。
Abstract:There are 11 parameters in the form of domestic integrated modeling of ballistic limit equations. Theoretically, the exhaustion method can be used to obtain the numerical value, but the computation time is too long and the storage space is huge, so it is not suitable to realize. To solve this problem, differential evolution algorithm is used. Based on the domestic data of stuffed Whipple shield, the differential evolution algorithm is applied to optimize 11 undetermined parameters of the formal ballistic limit equation of the integrated modeling. The optimization results show that the totality predicted rate is 82.35%, the safety predicted rate is 100%, and the average sum of squared prediction relative errors is 0.001 3. Based on 49 experimental data from other sources for predictive testing, the prediction test shows that the totality predicted rate is raised by 1.32%, the safety predicted rate is reduced by 4.08%, and the average sum of squared prediction relative errors is increased by 0.007 3. It shows that the differential evolution algorithm is suitable for solving the ba-llistic limit equation modeling of multiple parameters and multiple targets.
-
表 1 各函数优化结果
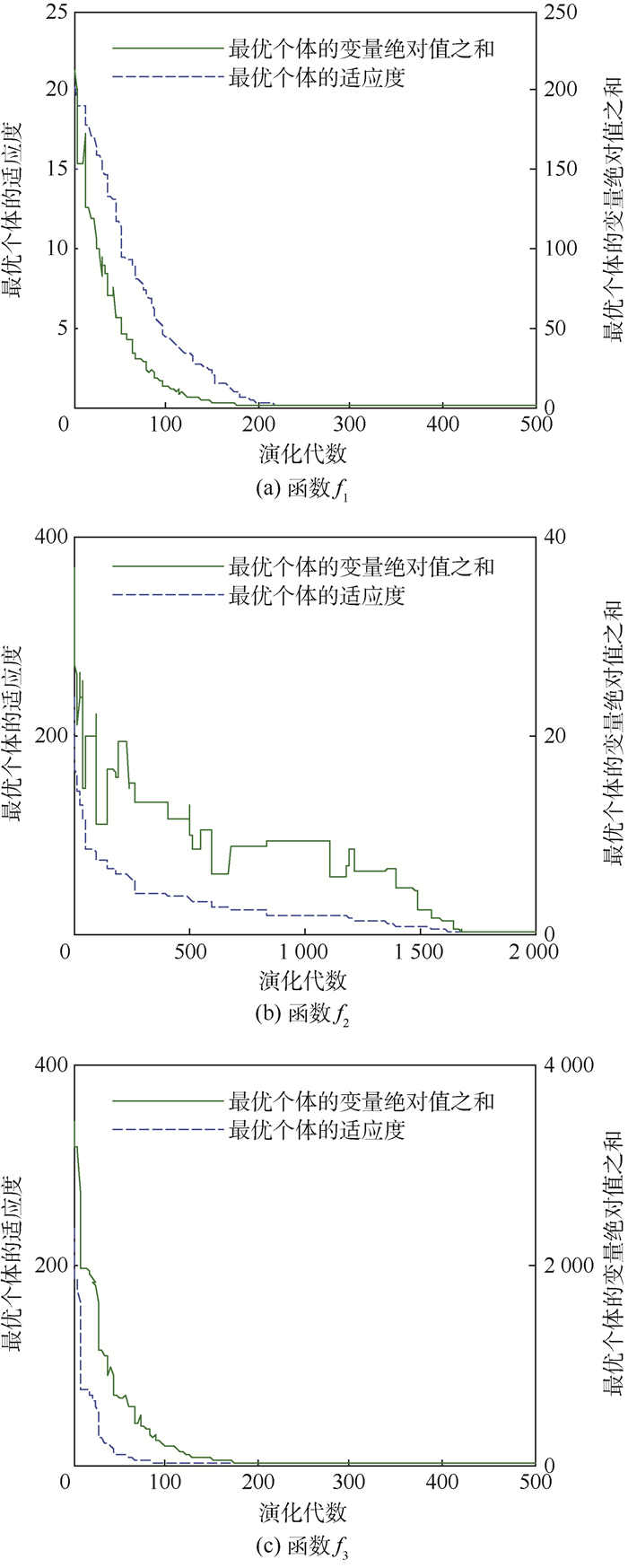
测试函数 理论最优值 演化代数 优化结果 f1 0 500 0.000 06 f2 0 2 000 0.000 01 f3 0 500 0.000 12 表 2 优化前后变量的数值比较
Table 2. Comparison of variable values before and after optimization
变量 初始值 优化值 x1 0.6 0.457 x2 0.3 0.4 x3 0.2 0.1 x4 -0.3 -0.311 x5 1 1.05 x6 0.3 0.25 x7 0.4 0.284 x8 1.2 1.5 x9 0.3 0.21 x10 0.2 0.11 x11 -0.25 -0.339 -
[1] 闫军, 郑世贵.填充式防护结构填充层撞击特性研究[J].载人航天, 2013, 19(1):10-14. http://www.cqvip.com/QK/90288X/201503/664014337.htmlYAN J, ZHENG S G.Study on impact characteristics of stuffed shielding structure[J].Manned Spaceflight, 2013, 19(1):10-14(in Chinese). http://www.cqvip.com/QK/90288X/201503/664014337.html [2] CHRISTIANSEN E, LAMBERT M, STOKES H.IADC protection manual[M].Bremen:Inter Agency Debris Committee, 2002. [3] 贾光辉, 欧阳智江, 蒋辉, 等.填充式防护结构弹道极限方程的多指标寻优[J].北京航空航天大学学报, 2013, 39(12):1573-1583. http://bhxb.buaa.edu.cn/CN/abstract/abstract12792.shtmlJIA G H, OUYANG Z J, JIANG H, et al.Multiple indicators optimization for stuffed whipple shield ballistic limit equation[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12):1573-1583(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract12792.shtml [4] 贾光辉, 欧阳智江, 蒋辉.撞击极限方程预测指标剖析与实例[J].航空学报, 2013, 34(10):2364-2371. http://mall.cnki.net/magazine/Article/HKXB201310004.htmJIA G H, OUYANG Z J, JIANG H.Analysis and instances of ballistic limit equations' predictive indicators[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(10):2364-2371(in Chinese). http://mall.cnki.net/magazine/Article/HKXB201310004.htm [5] CHRISTIANSEN E L, KERR J H.Ballistic limit equations for spacecraft shielding[J].International Journal of Impact Engineering, 2001, 26(1):93-104. http://cn.bing.com/academic/profile?id=b77bc399903309c9446b743c7bfafd98&encoded=0&v=paper_preview&mkt=zh-cn [6] STORN R, PRICE K. Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous spaces: TR-95-012[R]. Berkeley: University of California, 1995. [7] 陈良, 戴光明, 张全元, 等.差异演化及其改进形式的综述[J].计算机工程与设计, 2008, 29(1):131-134. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjgcysj200801041CHEN L, DAI G M, ZHANG Q Y, et al.Overview of differential evolution algorithm and its improved algorithms[J].Computer Engineering and Design, 2008, 29(1):131-134(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjgcysj200801041 [8] STORN R, PRICE K.Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization, 1997, 11(4):341-359. doi: 10.1023/A:1008202821328 [9] 姚光乐, 贾光辉.填充式防护结构弹道极限方程形式建模[J].空间碎片研究, 2017, 17(1):29-33. http://www.oalib.com/paper/4250102YAO G L, JIA G H.Formal modeling of ballistic limit equations for stuffed whipple shield[J].Space Debris Research, 2017, 17(1):29-33(in Chinese). http://www.oalib.com/paper/4250102 [10] 袁俊刚, 孙治国, 曲广吉.差异演化算法的数值模拟研究[J].系统仿真学报, 2007, 19(20):4646-4648. doi: 10.3969/j.issn.1004-731X.2007.20.011YUAN J G, SUN Z G, QU G J.Simulation study of differential evolution[J].Journal of System Simulation, 2007, 19(20):4646-4648(in Chinese). doi: 10.3969/j.issn.1004-731X.2007.20.011 [11] 汪勇, 徐琼, 张凌, 等.基于遗传分层序列法的云制造资源优化配置[J].统计与决策, 2016, 20:80-83. http://edu.wanfangdata.com.cn/Periodical/Detail/jsjkx201205007WANG Y, XU Q, ZHANG L, et al.Optimal allocation of cloud manufacturing resources based on genetic stratified sequence method[J].Statistics and Decision, 2016, 20:80-83(in Chinese). http://edu.wanfangdata.com.cn/Periodical/Detail/jsjkx201205007 [12] 张宝玺. 超高速撞击玄武岩及Kevlar纤维布填充防护结构优化设计[D]. 哈尔滨: 哈尔滨工业大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012002274.htmZHANG B X. The optimal structural design of stuffed shields with basalt and Kevlar fiber clothes on hypervelocity impacting[D]. Harbin: Harbin Institute of Technology, 2011(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10213-1012002274.htm [13] 哈跃. 玄武岩纤维材料及其填充防护结构超高速撞击特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. http://cdmd.cnki.com.cn/article/cdmd-10213-2011015844.htmHA Y. Research on hypervelocity impact properties of woven of basalt fiber and its stuffed shielding structure[D]. Harbin: Harbin Institute of Technology, 2009(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10213-2011015844.htm [14] 祖士明. 玄武岩及Kevlar纤维填充式防护结构超高速撞击性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D416804ZU S M. Research on hypervelocity impact performance of shielding structure stuffed with basalt and Kevlar fiber[D]. Harbin: Harbin Institute of Technology, 2013(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D416804 [15] 贾古寨, 哈跃, 庞宝君, 等.玄武岩/Kevlar纤维布填充防护结构撞击极限及损伤特性[J].爆炸与冲击, 2016, 36(4):433-440. doi: 10.11883/1001-1455(2016)04-0433-08JIA G Z, HA Y, PANG B J, et al.Ballistic limit and damage properties of basalt/Kevlar stuffed shield[J].Explosion and Shock Waves, 2016, 36(4):433-440(in Chinese). doi: 10.11883/1001-1455(2016)04-0433-08 -







 下载:
下载: