BLDC电机温度退化多段Wiener过程建模

袁庆洋; 叶建华; 李晓钢

doi:10.13700/j.bh.1001-5965.2017.0546

BLDC电机温度退化多段Wiener过程建模

doi: 10.13700/j.bh.1001-5965.2017.0546

北京航空航天大学可靠性与系统工程学院, 北京 100083

详细信息

作者简介:
袁庆洋  男, 硕士研究生。主要研究方向：产品环境工程

叶建华  男, 硕士, 工程师。主要研究方向：可靠性与环境试验技术

李晓钢  男, 博士, 教授, 硕士生导师。主要研究方向：可靠性试验技术、产品环境工程、加速试验

通讯作者:
叶建华, E-mail:yjhuan@buaa.edu.cn

中图分类号: TP202⁺.1
计量
- 文章访问数: 678
- HTML全文浏览量: 70
- PDF下载量: 388
- 被引次数: 0
出版历程
- 收稿日期: 2017-08-31
- 录用日期: 2017-10-20
- 网络出版日期: 2018-07-20

Multistage temperature degradation modeling for BLDC motor based on Wiener process

School of Reliability and Systems Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

More Information

Corresponding author: YE Jianhua, E-mail:yjhuan@buaa.edu.cn

摘要

摘要:
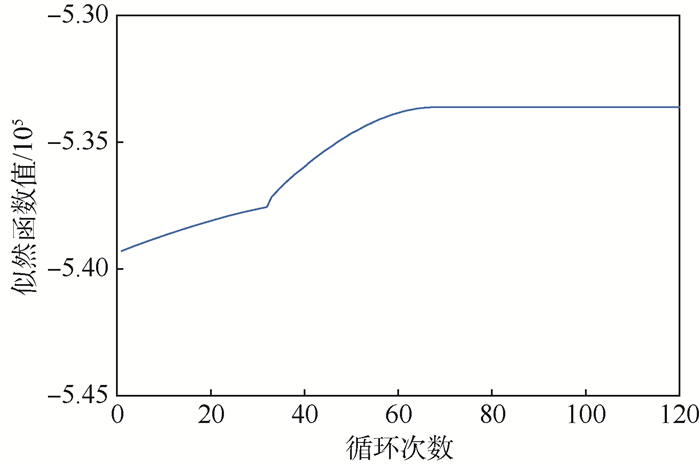
无刷直流（BLDC）电机应用广泛，其温度退化过程呈现多段性，需建立多段退化模型，而模型参数较多时，参数估计过程对初始值敏感且易陷入局部最优。首先，针对电机的加速退化数据进行研究，采用正态加权平均（Gauss滤波）的方式滤波，改进实际数据在模型参数的估计中的应用。然后，引入转换函数对Wiener模型改进，建立多段Wiener模型。其次，以极大化似然函数进行参数估计，计算时采用改进粒子群优化（PSO）算法得到估计值，对比非线性模型的残差的正态性，同时分析各模型理论寿命分布及实际该批次失效分布，确定多段模型合理性；得到的模型结果说明电机在退化过程中发生了退化机理的改变，且变换速度快。最后，以非线性模型不同时刻的寿命分布给出该应力下电机的寿命预测，这对电机的预测与健康管理（PHM）有重要意义。
- 无刷直流(BLDC)电机 /
- 退化建模 /
- 多段Wiener过程 /
- 单纯形自优化粒子群优化(PSO)算法 /
- 预测与健康管理(PHM)
Abstract:
Brushless DC(BLDC) motor is widely used and its temperature degradation process is multistage. It is necessary to establish a multistage degradation model. When the model has several parameters, the parameter estimation process is sensitive to the initial value and easy to end up with a local optimization. This study was based on accelerated degradation data of motors. The normal weighted average filter (Gauss filter) was used to improve the results of estimation for the model parameters. A multistage Wiener model was established by using the transition function to modify linear model. Then, to maximize likelihood function for parameter estimation, the numerical optimization method, improved particle swarm optimization (PSO), was used for cycle calculation. The rationality of multistage model is verified by comparison of the normality of residual with widely used nonlinear Wiener model, and by analysis of theoretical life distribution of models and actual failure distribution of this batch. The modeling results show that the degradation mechanism changes at high speed during the degradation of the motor. Finally, prediction for motor life under this stress was gained by life distribution in different moments of time calculated by nonlinear model, which is important for the prognostics and health management (PHM) of motors.
- brushless DC(BLDC) motor /
- degradation modeling /
- multistage Wiener process /
- particle swarm optimization (PSO) algorithm with simplex method /
- prognostics and health management (PHM)

HTML全文

图 1 似然函数值在循环中的优化过程

Figure 1. Optimization process of likelihood function value in loop

下载: 全尺寸图片幻灯片

图 2 不同Wiener模型漂移过程对比

Figure 2. Comparison of drift processes in different Wiener models

下载: 全尺寸图片幻灯片

图 3 不同Wiener模型理论失效分布对比

Figure 3. Comparison of theoretical failure distribution in different Wiener models

下载: 全尺寸图片幻灯片

图 4 不同Wiener模型残差分布对比

Figure 4. Comparison of residual distributions in different Wiener models

下载: 全尺寸图片幻灯片

图 5 多段模型所得剩余寿命分布预测

Figure 5. Prediction of remaining life distribution by multistage model

下载: 全尺寸图片幻灯片

表 1 增量值分布

Table 1. Distribution of increment values

退化增量范围	数量
[-0.1, 0.1)	22
[-0.2, -0.1)∪[0.1, 0.2)	19
[-0.3, -0.2)∪[0.2, 0.3)	8
[-0.4, -0.3)∪[0.3, 0.4)	1
(-∞, -0.4)∪[0.4, -∞)	0

下载: 导出CSV

参考文献(17)

[1]	张琛.直流无刷电动机原理及应用[M].北京:机械工业出版社, 2004:1-2. ZHANG C.The principle and application of brushless DC motor[M].Beijing:China Machine Press, 2004:1-2(in Chinese).
[2]	王玲玲, 茆诗松, 王静.电动机平均寿命的零失效验收方案[J].应用概率统计, 1995(4):439-442. http://www.cqvip.com/QK/96556X/199504/1940173.html WANG L L, MAO S S, WANG J.Zero failure acceptance scheme for average life of motor[J].China Chinese Journal of Applied Probability and Statistics, 1995(4):439-442(in Chinese). http://www.cqvip.com/QK/96556X/199504/1940173.html
[3]	王剑, 翁雷, 张慧.基于加速环境的可靠性指标验证试验[J].电子产品可靠性与环境试验, 2010, 28(4):6-10. http://www.cqvip.com/qk/91716X/201004/34992691.html WANG J, WENG L, ZHANG H.The accelerated testing to estimate the reliability specifications[J].Electronic Product Reliability and Environmental Testing, 2010, 28(4):6-10(in Chinese). http://www.cqvip.com/qk/91716X/201004/34992691.html
[4]	WANG W.A model for residual life prediction based on Brownian motion with an adaptive drift[J].Microeletronics Reliability, 2011, 51(2):285-293. doi: 10.1016/j.microrel.2010.09.013
[5]	WHITMORE G A.Modelling accelerated degradation data using Wiener diffusion with a time scale transformation[J].Lifetime Data Analysis, 1997, 3:27-45. doi: 10.1023/A:1009664101413
[6]	TSENG S T, PENG C Y.Stochastic diffusion modeling of degradation data[J].Journal of Data Science, 2007, 5:315-333. http://cn.bing.com/academic/profile?id=9d5b9b7e374dc0c7f7f6b91d2a5edc73&encoded=0&v=paper_preview&mkt=zh-cn
[7]	SI X S, WANG W B, HU C H, et al.Remaining useful life estimation based on a nonlinear diffusion degradation process[J].IEEE Transactions on Reliability, 2012, 61(1):50-67. doi: 10.1109/TR.2011.2182221
[8]	王小林, 蒋平, 邢云燕, 等.非线性退化情况下的产品剩余寿命预测[M].北京:国防工业出版社, 2015:39-46. WANG X L, JIANG P, XING Y Y, et al.Residual life estimation for nonlinear-deterioriate products[M].Beijing:National Defense Industry Press, 2015:39-46(in Chinese).
[9]	蒋同敏.可靠性与寿命试验[M].北京:国防工业出版社, 2012:346-354. JIANG T M.Reliability maintainability supportability[M].Beijing:National Defense Industry Press, 2012:346-354(in Chinese).
[10]	历海涛, 金光, 周经伦, 等.动量轮维纳过程退化建模与寿命分析[J].航空动力学报, 2011, 26(3):623-627. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkdlxb201103022 LI H T, JIN G, ZHOU J L, et al.Momentum wheel Wiener process[J].Journal of Aerospace Power, 2011, 26(3):623-627(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkdlxb201103022
[11]	王书锋, 王友仁, 姜媛媛.Wiener过程性能退化电子产品的剩余寿命预测方法[J].电子测量技术, 2014, 37(5):17-20. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014268601.htm WANG S F, WANG Y R, JIANG Y Y.Residual life prediction method of electronic products with Wiener process degradation[J].Electronic Measurement Technology, 2014, 37(5):17-20(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10487-1014268601.htm
[12]	陈逸成, 何华锋, 邓会选, 等.基于Kalman滤波和Wiener过程的系统性能退化数据建模方法[J].电光与控制, 2015, 22(7):107-110. http://www.cqvip.com/QK/91481X/201507/665350013.html CHEN Y C, HE H F, DENG H X, et al.A system degradation modeling method based on Kalman filter and Wiener process[J].Electronics Optics & Control, 2015, 22(7):107-110(in Chinese). http://www.cqvip.com/QK/91481X/201507/665350013.html
[13]	LONNIE C L. 随机过程: 滤波、估计与检测[M]. 邱天爽, 李婷, 毕英伟, 等译. 北京: 电子工业出版社, 2015: 130-135. LONNIE C L. Random processes: Filtering estimation and detection[M]. QIU T S, LI T, BI Y W, et al, translated. Beijing: Publishing House of Electronics Industry, 2005: 130-135(in Chinese).
[14]	赵春燕.平滑转换自回归模型的理论与应用研究[M].北京:清华大学出版社, 2015:28-29. ZHAO C Y.Research on the thoery and application of smooth transition autoregressive mode[M].Beijing:Tsinghua University Press, 2015:28-29(in Chinese).
[15]	郑伟博, 张纪会.基于Nelder-Mead单纯形法的改进量子行为粒子群算法[J].复杂系统与复杂性科学, 2016, 13(6):97-104. http://www.cqvip.com/QK/87154X/201602/668862608.html ZHENG W B, ZHANG J H.A improved quantum behaved particle swarm optimization algorithm rsing Nelder and Mead's simplex algorithm[J].Complex Sestems and Comples Science, 2016, 13(6):97-104(in Chinese). http://www.cqvip.com/QK/87154X/201602/668862608.html
[16]	JORGE N, STEPHEN J W.Numerical optimization[M].2nd ed.Berlin:Springer, 1999:363-378.
[17]	杨振海, 程维虎, 张军舰.拟合优度检验[M].北京:科学出版社, 2011:15-19. YANG Z H, CHENG W H, ZHANG J J.Goodness of fit test[M].Beijing:Science Press, 2011:15-19(in Chinese).