Mechanism and experimental research on fluid flow in annulus of coaxial rotating conical cylinders
-
摘要:
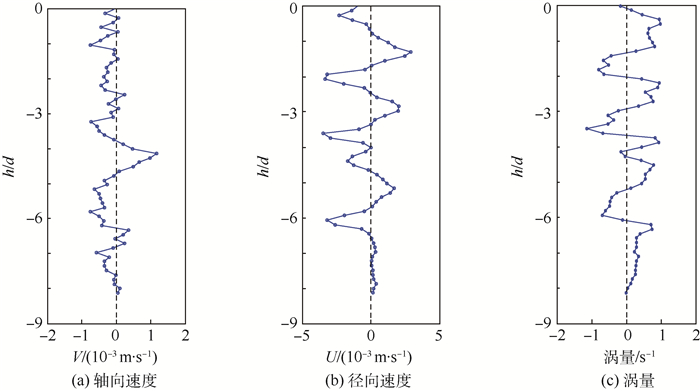
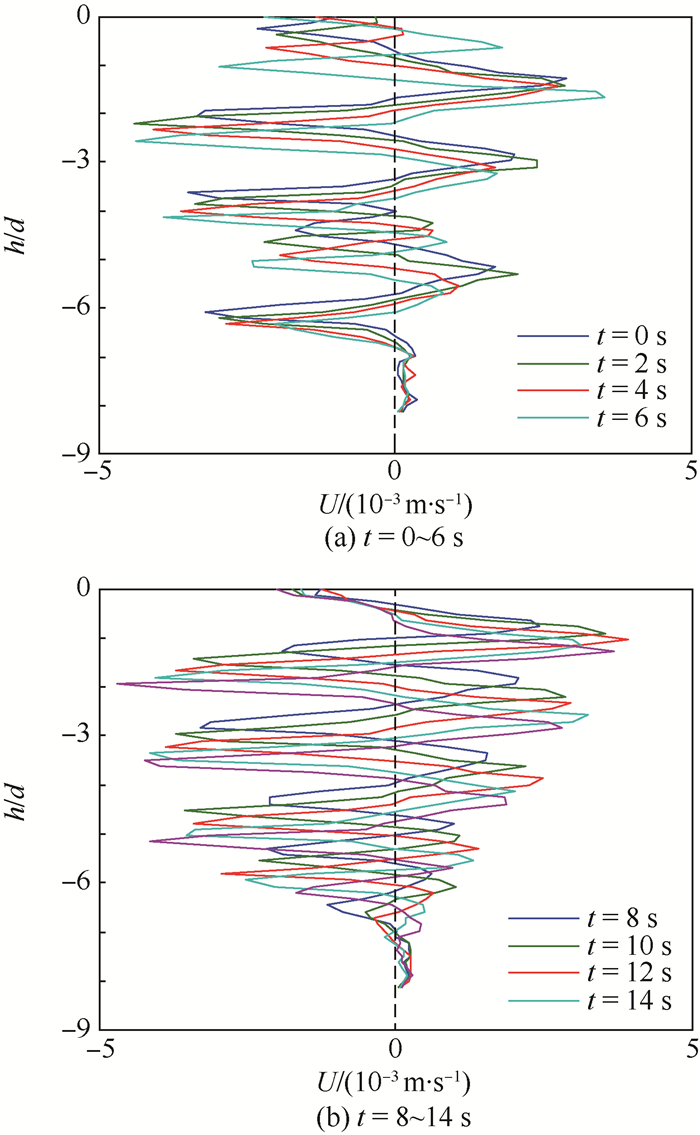
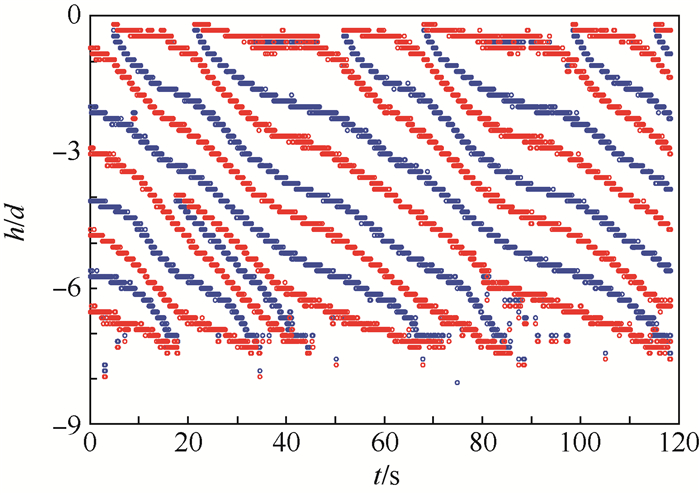
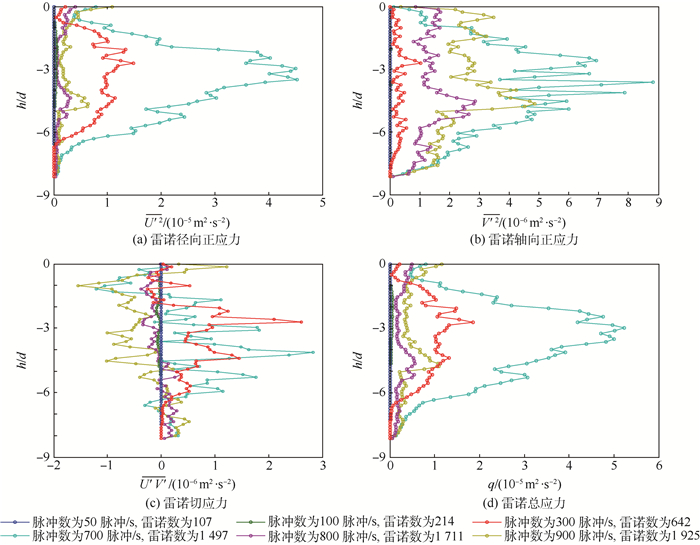
同轴旋转圆台环隙内流体的流动是基于经典的两同轴旋转圆柱环隙内泰勒库特流的一种扩展研究。通过流动显示实验和PIV粒子图像测速技术对圆台环隙的内部流场进行可视化和定量化的研究，分析涡运动的周期性规律，探究圆台环隙内雷诺应力分布和水位高度对流场的影响。研究表明，随着时间的发展，涡列周期性明显且整体在下移，当脉冲数为100脉冲/s时，环隙内形成均匀分布的正反交替的涡；当脉冲数为200~500脉冲/s时，存在快慢交替的分裂周期；在3种水位高度下也都存在明显周期性分裂，只是周期时间和涡的个数不同；平均流场存在上凸型外向流和下凹型内向流2种流态，流态的差异是离心力与静压力双重作用的强弱变化所致；雷诺应力分布中，径向正应力占主导，并主要集中在环隙中部。
Abstract:The research on the flow fluid in the annulus of coaxial rotating conical cylinders originates from the classical Taylor Couette flow in the annulus of two coaxial rotating conical cylinders. This paper uses flow visualization experiments and PIV to display and quantify the internal flow field in the annulus of conical cylinders, and the periodic trends of vortex motions are studied to explore the effect of in-annulus Reynolds stress distribution and water level on the flow field. The study indicates that the periodic trends of vortex column move downward over time, and a series of alternate clockwise and anticlockwise vortices are uniformly distributed inside the annulus where pulse number is 100 pulse/s. There exists the alternating vortex fracture periods where pulse number is between 200-500 pulse/s. Under three different water levels, there exists obvious periodic fracture, but the periodic time and number of vortices are different. There are two types of flow (up-convex outward flow and down-concave inward flow) in the mean flow field, and the type of flow is decided by centrifugal force and static pressure. Radial normal stress dominates in Reynolds stress distribution and mainly exists in the middle of the annulus.
-
Key words:
- coaxial rotating conical cylinder /
- Taylor Couette flow /
- PIV /
- Reynolds stress /
- fracture period
-
图 9 子午面处涡变化历程(200脉冲/s)
Figure 9. Vortex transformation process on meridian plane (200 pulse/s)
表 1 脉冲数和内筒转速匹配
Table 1. Matching of pulse number and inner cylinder revolving speed
脉冲数/(脉冲·s-1) 内筒转速/(r·min-1) 雷诺数 h=140 mm h=120 mm h=100 mm 100 1.88 214 195 177 200 3.75 428 390 354 300 5.64 642 586 531 500 9.40 1 070 976 885 
下载: 导出CSV
表 2 螺旋涡运动周期
Table 2. Motion period of spiral vortices
脉冲数/(脉冲·s-1) 内筒转速/(r·min-1) 快分裂周期/s 慢分裂周期/s 总分裂周期/s 100 1.88 29 29 58 200 3.75 17 30 47 300 5.64 7 25 32 500 9.40 8 12 20
下载: 导出CSV
-
[1] RAYLEIGH L.On the dynamics of revolving fluids[J].Proceedings of the Royal Society of London, 1917, 93(648):148-154. doi: 10.1098/rspa.1917.0010 [2] MARGARITIS A, WILKE C R.The rotorfermentor.1.Description of the apparatus, power requirements and mass transfer characteristics[J].Biotechnology and Bioengineering, 1978, 20(5):709-713. doi: 10.1002/(ISSN)1097-0290 [3] HALLSROM D, LOPEZ-LEIVA M.Description of a rotating ultrafiltration module[J].Desalination, 1978, 24(1-3):273-279. doi: 10.1016-S0011-9164(00)88089-3/ [4] LOPEZ-LEIVA M.Ultrafiltration at low degrees of concentration polarization:Technical possibilities[J].Desalination, 1980, 35:115-128. doi: 10.1016/S0011-9164(00)88606-3 [5] 林彦军, 李殿卿, 李峰, 等. 一种旋转液膜反应器及其在制备层状复合金属氢氧化物中的应用: CN201210105567. 6[P]. 2013-12-25.LIN Y J, LI D Q, LI F, et al. A rotating liquid membrane reactor and its application in the preparation of layered composite metal hydroxide: CN201210105567. 6[P]. 2013-12-25(in Chinese). [6] JIAO Q Z, YUN Z, HUI X, et al.Intercalation and selective IR adsorption of hydrotalcite[J].Chinese Journal of Applied Chemistry, 2002, 19(10):1011-1013. https://www.researchgate.net/publication/292411722_Intercalation_and_selective_IR_adsorption_of_hydrotalcite [7] 李雪. 旋转液膜反应器内流场的研究[D]. 北京: 北京化工大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2862467LI X. Flow field in rotating liquid membrane reactor[D]. Beijing: Beijing University of Chemical Technology, 2014(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2862467 [8] TAYLOR G I.Stability of a viscous liquid contained between two rotating cylinders[J].Philosophical Transactions of the Royal Society of London, 1923, 223:289-343. doi: 10.1098/rsta.1923.0008 [9] COLES D.Transition in circular Couette flows[J].Journal of Fluid Mechanics, 1965, 21:385-425. doi: 10.1017/S0022112065000241 [10] ANDERECK C D, LIU S S, SWINNEY H L.Flow regimes in a circular Couette system with in-dependently rotating cylinders[J].Journal of Fluid Mechanics, 1986, 164:155-183. doi: 10.1017/S0022112086002513 [11] WIMMER M.An experimental investigation of Taylor vortices flow between conical cylinders[J].Journal of Fluid Mechanics, 1995, 292:205-227. doi: 10.1017/S0022112095001492 [12] NOUI-MEHIDI M N, OHMURA N.Mechanism of mode selection for Taylor vortices flow between co-axial conical rotating cylinders[J].Journal of Fluids and Structures, 2002, 16(2):247-262. doi: 10.1006/jfls.2001.0417 [13] 文普. 同轴旋转圆台间流体流动的理论研究和数值模拟[D]. 北京: 北京化工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10010-2010169759.htmWEN P. The theoretical study and numerical simulation of fluid flow between coaxial rotary cylinder[D]. Beijing: Beijing University of Chemical Technology, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10010-2010169759.htm [14] 张艺晓. 同轴旋转圆台间流体流动的动力学研究[D]. 北京: 北京化工大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10010-1012414250.htmZHANG Y X. Study on dynamic flow of fluid flow between coaxial rotating cylinder[D]. Beijing: Beijing University of Chemical Technology, 2012(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10010-1012414250.htm [15] 李华鹏. 非平行环隙同轴旋转圆台间流体流动的数值模拟和理论分析[D]. 北京: 北京化工大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2628970LI H P. Numerical simulation and theoretical analysis of fluid flow between non-parallel annulus coaxial rotating circular table[D]. Beijing: Beijing University of Chemical Technology, 2014(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2628970 -
下载:
点击查看大图
计量
- 文章访问数: 655
- HTML全文浏览量: 148
- PDF下载量: 519
- 被引次数: 0
