-
摘要:
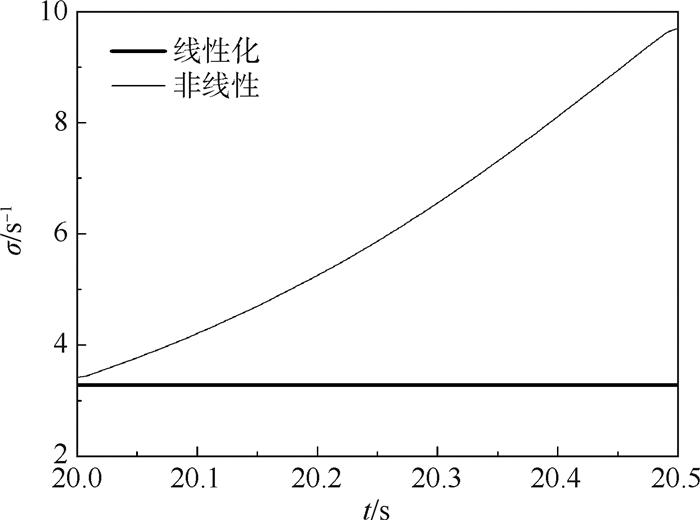
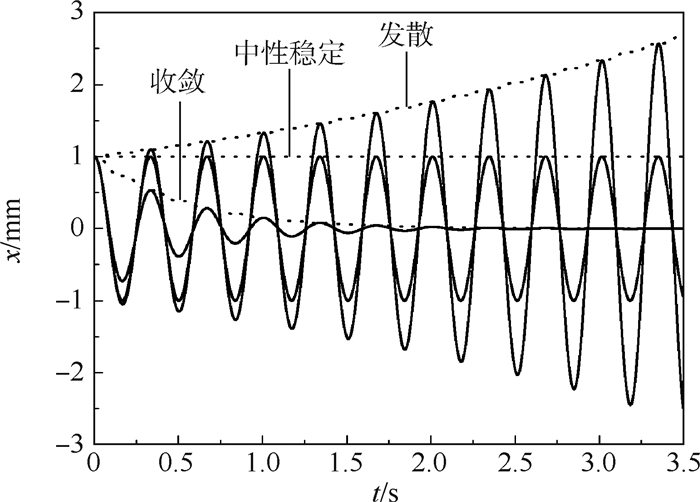
针对现有适于宽幅值范围的黏弹减摆器模型一般含有动幅值参量，不便用于幅值变化的直升机旋翼/机体耦合动稳定性时域分析的问题，给出了小摆振阻尼比时，黏弹减摆器在单频及双频条件下动幅值参量的计算方法，运用该方法计算系统在收敛、中性稳定及发散3种情况下的幅值曲线，较好地反映了响应幅值在时域上的变化趋势。将改进的黏弹减摆器模型用于直升机地面共振非线性时域分析，为准确获取旋翼摆振后退型响应，给出了所需桨叶激振力矩的计算方法，在不同转速不同复模量状态下，采用该方法确定的激振力矩对桨叶进行激振激出的响应幅值与预期值误差不超过6%。对摆振后退型响应进行分析可知，系统稳定时，与线性化结果相比，计入黏弹减摆器非线性后，旋翼摆振后退型响应衰减更快，其模态阻尼在时域上呈增加趋势。
Abstract:The existing elastomeric damper models commonly introduce dynamic amplitude parameter for applying to wide amplitude situation. It is inconvenient to time domain analysis of helicopter rotor-fuselage coupled dynamic stability on account of the dynamic amplitude changing in time domain. Aimed at this problem, the calculation methods of dynamic amplitude parameter were given for single and double frequency excitation cases while the lagging damping ratio is little. The amplitude curves calculated by the method describe the response amplitudes well while the system is in the state of convergence, neutral stable, or divergence. The improved model of elastomeric damper was used for nonlinear time domain analysis of helicopter ground resonance. The calculation method of excitation moment at blade was given for exciting the regressive lagging mode responses accurately. For different rotor speeds and complex modulus states, the response amplitudes excited by the excitation moment determined by the moment calculation method were compared with the desired values, and the maximum error is under 6%. After the regressive lagging mode responses are analyzed, it is known that the regressive lagging mode responses decay faster than the linearization results, and its modal damping increases in time domain due to the elastomeric damper nonlinearity while system is stable.
-
Key words:
- helicopter /
- elastomeric damper /
- nonlinear /
- time domain analysis /
- ground (air) resonance
-
图 1 不同稳定情况下的单频时域响应
Figure 1. Single frequency response in time domain at different stable situations
图 2 不同稳定情况下的双频时域响应
Figure 2. Double frequency response in time domain at different stable situations
图 3 黏弹减摆器时域响应计算流程
Figure 3. Calculation flow of elastomeric damper time domain response
图 10 旋翼摆振后退型阻尼随时间变化情况
Figure 10. Variation of rotor regressive lagging modal damping with time
表 1 直升机主要参数
Table 1. Main parameters of helicopter
参数 数值 桨叶片数 4 桨叶质量/kg 42.3 桨叶对摆振铰静矩/(kg·m) 123.7 桨叶对摆振铰惯性矩/(kg·m2) 457 摆振铰外伸量/m 0.23 减摆器到摆振铰距离/m 0.35 机体纵向当量质量/kg 2 000 机体纵向固有频率/Hz 1 机体纵向当量阻尼/(N·s·m-1) 1 000 机体横向当量质量/kg 800 机体横向固有频率/Hz 1.5 机体横向当量阻尼/(N·s·m-1) 500 
下载: 导出CSV
-
[1] FELKER F F, LAU B H, MCLAUGHLIN S, et al.Nonlinear behavior of an elastomeric lag damper undergoing dual-frequency motion and its effect on rotor dynamics[J].Journal of the American Helicopter Society, 1987, 34(4):45-53. http://www.ingentaconnect.com/content/ahs/jahs/1987/00000032/00000004/art00005 [2] KUNZ D L. Influence of elastomeric lag damper modeling on the predicted dynamic response of helicopter rotor systems[C]//Proceedings of 38th Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 1997: 1-11. [3] 胡国才, 侯志强.一种基于复模量的黏弹减摆器非线性VKS改进模型[J].工程力学, 2005, 22(Sup.):73-77. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=GCLX2005S1012&dbname=CJFD&dbcode=CJFQHU G C, HOU Z Q.An improved nonlinear VKS model of elastomeric lag damper based on its complex modulus[J].Engineering Mechanics, 2005, 22(Sup.):73-77(in Chinese). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=GCLX2005S1012&dbname=CJFD&dbcode=CJFQ [4] LESIEUTRE G A.Modeling frequency-dependent longitudinal dynamic behavior of linear viscoelastic long fiber composites[J].Journal of Composite Materials, 1994, 28(18):1770-1782. doi: 10.1177/002199839402801802 [5] LESIEUTRE G A, BIANCHINI E.Time domain modeling of linear viscoelasticity using anelastic displacement fields[J].Journal of Vibration and Acoustics, 1995, 117(4):424-430. doi: 10.1115/1.2874474 [6] SMITH E C, GOVINDSWAMY K, BCALE M R, et al.Formulation, validation, and application of a finite element model for elastomeric lag dampers[J].Journal of the American Helicopter Society, 1996, 43(3):257-266. https://www.mendeley.com/research-papers/formulation-validation-application-finite-element-model-elastomeric-lag-dampers/ [7] BRACKBILL C R, LESIEUTRE G A, SMITH E C, et al.Characterization and modeling of the low strain amplitude and frequency dependent behavior of elastomeric damper materials[J].Journal of the American Helicopter Society, 2000, 47(1):34-42. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ028388022 [8] CAUGHEY T K.Equivalent linearization techniques[J].Journal of the Acoustical Society of America, 1963, 35(11):1706-1711. doi: 10.1121/1.1918794 [9] BOUC R. Forced vibration of mechanical system with hysteresis[C]//Proceedings of 4th Conference on Nonlinear Oscillation, 1967: 315-320. [10] WEN Y K.Method for random vibration of hysteretic systems[J].Journal of Applied Mechanics, 1976, 102(2):249-263. https://www.mendeley.com/research-papers/method-random-vibration-hysteretic-systems/ [11] 李冬伟, 白鸿柏, 杨建春, 等.非线性迟滞系统建模方法[J].机械工程学报, 2005, 41(10):205-214. doi: 10.3321/j.issn:0577-6686.2005.10.040LI D W, BAI H B, YANG J C, et al.Modeling of a nonlinear system with hysteresis characteristics[J].Chinese Journal of Mechanical Engineering, 2005, 41(10):205-214(in Chinese). doi: 10.3321/j.issn:0577-6686.2005.10.040 [12] GANDHI F, CHOPRA I.An analytical model for a nonlinear elastomeric lag damper and its effect on aeromechanical stability in hover[J].Journal of the American Helicopter Society, 1994, 39(4):59-69. doi: 10.4050/JAHS.39.59 [13] 胡国才, 向锦武, 张晓谷.黏弹减摆器非线性特性对直升机前飞空中共振的影响分析[J].航空学报, 2005, 26(2):199-202. doi: 10.3321/j.issn:1000-6893.2005.02.015HU G C, XIANG J W, ZHANG X G.Analysis of the effect of nonlinear characteristics of elastomeric lag damper on helicopter air resonance in forward flight[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(2):199-202(in Chinese). doi: 10.3321/j.issn:1000-6893.2005.02.015 [14] 王波, 李书, 徐亚妮.不同黏弹减摆器连接的直升机地面共振分析[J].振动工程学报, 2007, 20(2):123-127. doi: 10.3969/j.issn.1004-4523.2007.02.004WANG B, LI S, XU Y N.Analysis of ground resonance for helicopters with different elastomeric lag damper connections[J].Journal of Vibration Engineering, 2007, 20(2):123-127(in Chinese). doi: 10.3969/j.issn.1004-4523.2007.02.004 [15] 王波, 李书, 张晓谷.非线性叶间黏弹减摆器对直升机空中共振的影响分析[J].航空学报, 2007, 28(3):550-555. doi: 10.3321/j.issn:1000-6893.2007.03.008WANG B, LI S, ZHANG X G.Influence analysis of helicopter air resonance with nonlinear inter blade viscoelastic dampers[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(3):550-555(in Chinese). doi: 10.3321/j.issn:1000-6893.2007.03.008 [16] 卫丽君, 李书, 王波.黏弹减摆器结构参数对直升机动稳定性的影响分析[J].南京航空航天大学学报, 2010, 42(3):303-306. doi: 10.3969/j.issn.1005-2615.2010.03.008WEI L J, LI S, WANG B.Joint parameter analysis of helicopter dynamic stability with viscoelastic dampers[J].Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3):303-306(in Chinese). doi: 10.3969/j.issn.1005-2615.2010.03.008 [17] 胡海岩.机械振动基础[M].北京:北京航空航天大学出版社, 2005:20-21.HU H Y.Fundamentals of mechanical vibration[M].Beijing:Beihang University Press, 2005:20-21(in Chinese). [18] 胡国才.直升机旋翼非线性等效阻尼的识别[J].航空学报, 2005, 26(3):303-307. doi: 10.3321/j.issn:1000-6893.2005.03.010HU G C.Nonlinear equivalent damping identification for helicopter rotor[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(3):303-307(in Chinese). doi: 10.3321/j.issn:1000-6893.2005.03.010 -
下载:
点击查看大图
计量
- 文章访问数: 597
- HTML全文浏览量: 84
- PDF下载量: 295
- 被引次数: 0
