基于柔性铰链的二自由度微动平台分析及优化

周睿; 周辉; 桂和利; 董虎; 曹毅

doi:10.13700/j.bh.1001-5965.2017.0706

基于柔性铰链的二自由度微动平台分析及优化

doi: 10.13700/j.bh.1001-5965.2017.0706

周睿^{1, 2},
周辉^{1, 2},
桂和利^{1, 3},
董虎^{1, 2},
曹毅^{1, 2, ,}

1.
江南大学机械工程学院, 无锡 214122
2.
江苏省食品先进制造装备技术重点实验室, 无锡 214122
3.
无锡科技职业学院, 无锡 214151

基金项目:

国家自然科学基金 50905075

江苏省“六大人才高峰”计划 ZBZZ-012

江苏省普通高校专业学位研究生实践创新计划 SJZZ16-0212

详细信息

作者简介:
周睿女, 硕士研究生。主要研究方向:柔性铰链及其应用

曹毅男, 博士, 教授, 硕士生导师。主要研究方向:机器人机构学及机器人技术

通讯作者:
曹毅.E-mail:caoyi@jiangnan.edu.cn

中图分类号: V414.5;TH122
计量
- 文章访问数: 758
- HTML全文浏览量: 204
- PDF下载量: 541
- 被引次数: 0
出版历程
- 收稿日期: 2017-11-13
- 录用日期: 2018-01-19
- 网络出版日期: 2018-09-20

Analysis and optimization of 2-DOF micro-positioning stage based on flexible hinges

ZHOU Rui^{1, 2},
ZHOU Hui^{1, 2},
GUI Heli^{1, 3},
DONG Hu^{1, 2},
CAO Yi^{1, 2
, ,}

1.
School of Mechanical Engineering, Jiangnan University, Wuxi 214122
2.
Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi 214122, China
3.
Wuxi Vocational College of Science and Technology, Wuxi 214151, China

Funds:

National Natural Science Foundation of China 50905075

the Six Talent Peaks Project in Jiangsu Province ZBZZ-012

the Research and the Innovation Project for College Graduates of Jiangsu Province SJZZ16-0212

More Information

Corresponding author: CAO Yi.E-mail:caoyi@jiangnan.edu.cn

摘要

摘要:
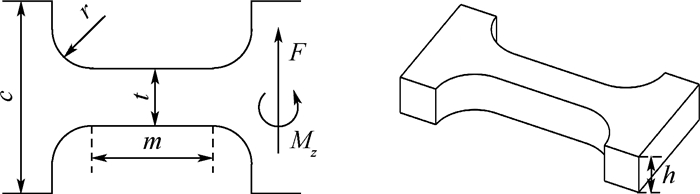
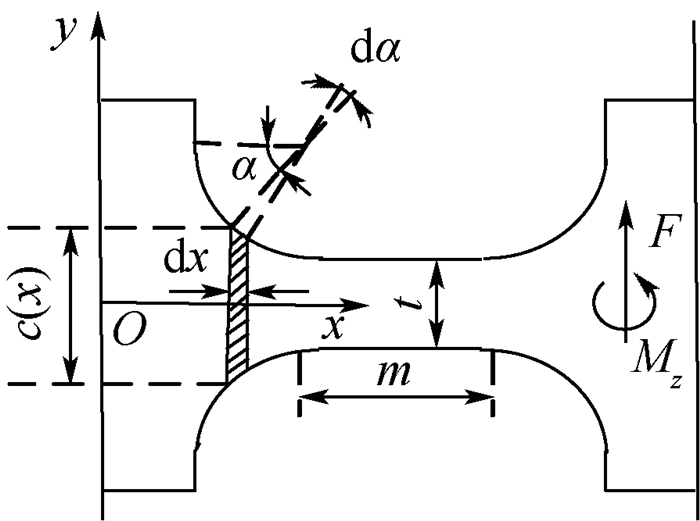
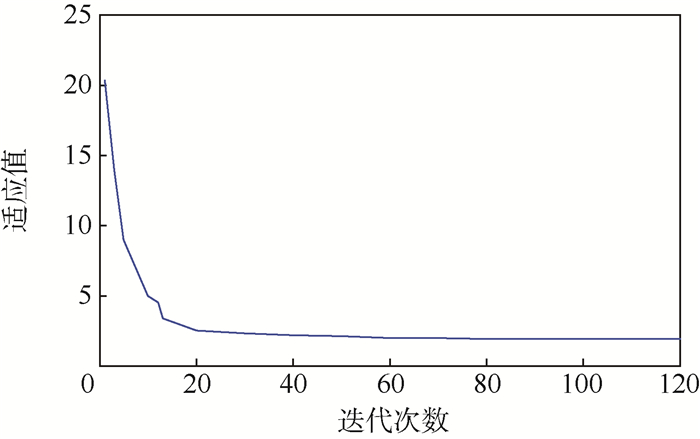
为改进微动平台的动态特性，提出了一种解耦的基于柔性铰链的二自由度微动平台。首先，综合考虑倒圆角直梁型柔性铰链与微动平台的结构特点，设计了一种新型的二自由度微动平台; 其次，推导了该微动平台的等效刚度计算模型，并通过理论计算与有限元仿真分析对比，验证了理论模型的正确性; 同时探讨了各结构参数对微动平台等效刚度的影响，并进行了灵敏度对比和分析; 再次，以提高二自由度微动平台的等效刚度为目标，建立了其优化设计模型，并采用自适应粒子群优化算法对该微动平台的主要结构参数进行了优化。最后，理论计算了该微动平台的固有频率，并通过有限元仿真分析验证了其正确性。上述分析证明了该机构的可行性及有效性。
- 二自由度微动平台 /
- 倒圆角直梁型柔性铰链 /
- 有限元分析 /
- 参数优化 /
- 固有频率
Abstract:
In order to improve the dynamic characteristics of the micro-positioning stage, a decoupled two-degree-of-freedom (2-DOF) parallel flexure-hinge micro-positioning stage is proposed. First, a new type of 2-DOF micro-positioning stage is designed based on the structure characteristics of the corner-filleted flexure hinge and micro-positioning stage. Second, the equivalent stiffness model of the micro-positioning stage is deduced, and the correctness of the theoretical model is verified by comparing the theoretical results with the finite element simulation. And at the same time, the influence of different structural parameters on micro-positioning stage is discussed, and the sensitivity comparison and analysis are conducted. Then, to improve the 2-DOF micro-positioning platform equivalent stiffness as the goal, the optimization model is established, and the adaptive particle swarm optimization algorithm is used to optimize the main structure parameters of the micro-positioning stage. Finally, the natural frequency of the stage is calculated, and its correctness is verified by finite element simulation. The above analysis proves the feasibility and effectiveness of the mechanism.
- 2-DOF micro-positioning stage /
- corner-filleted flexure hinge /
- finite element analysis /
- parameter optimization /
- natural frequency

HTML全文

图 1 二自由度微动平台

Figure 1. 2-DOF micro-positioning stage

下载: 全尺寸图片幻灯片

图 2 倒圆角直梁型柔性铰链

Figure 2. Corner-filleted flexure hinge

下载: 全尺寸图片幻灯片

图 3 倒圆角直梁型柔性铰链的受力分析

Figure 3. Force analysis of corner-filleted flexure hinge

下载: 全尺寸图片幻灯片

图 4 二自由度微动平台结构平面

Figure 4. Structure plan of 2-DOF micro-positioning stage

下载: 全尺寸图片幻灯片

图 5 复合平行四杆机构

Figure 5. Compound parallel four-bar mechanism

下载: 全尺寸图片幻灯片

图 6 微动平台仿真模型

Figure 6. Simulation model of micro-positioning stage

下载: 全尺寸图片幻灯片

图 7 x轴方向力-形变关系

Figure 7. Relationship between x-axis force and displacement

下载: 全尺寸图片幻灯片

图 8 结构参数与等效刚度k的关系

Figure 8. Relationship between structural parameters and equivalent stiffness k

下载: 全尺寸图片幻灯片

图 9 自适应粒子群优化算法适应度曲线

Figure 9. Fitness curve of adaptive particle swarm optimization algorithm

下载: 全尺寸图片幻灯片

图 10 微动平台的各阶振型

Figure 10. Various modes of vibration of micro-positioning stage

下载: 全尺寸图片幻灯片

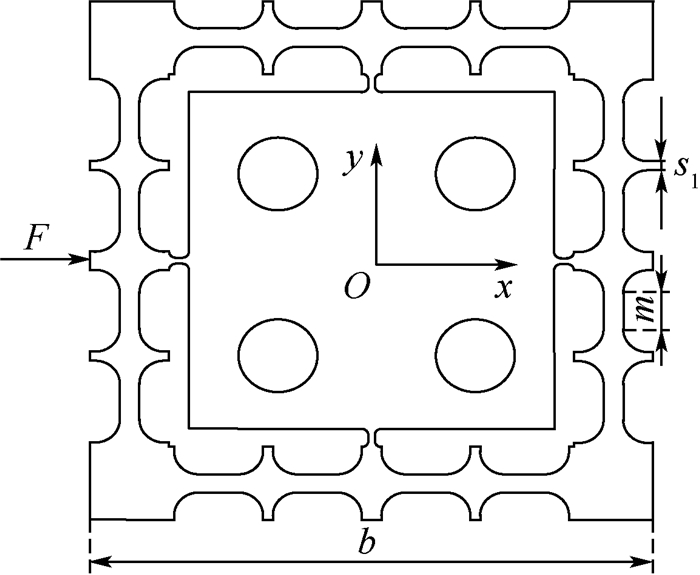
表 1 二自由度微动平台结构参数

Table 1. Structural parameters of 2-DOF micro-positioning stage

mm
参数	b	s₁	m	r	t	h
数值	85	3.3	3.3	4	2	20

下载: 导出CSV

表 2 x轴方向位移仿真值、理论值及其相对误差

Table 2. x-axis displacement simulation value, theoretical value and its relative error

力/N	x轴方向位移
力/N	理论值/(10^-7m)	仿真值/(10^-7m)	相对误差/%
2	1.048 8	1.065 3	1.57
4	2.097 5	2.132 5	1.67
6	3.146 3	3.197 0	1.61
8	4.195 1	4.260 7	1.56
10	5.243 8	5.320 2	1.46
12	6.286 4	6.376 3	1.43
14	7.342 3	7.443 6	1.38
16	8.396 5	8.509 0	1.34
18	9.390 2	9.511 3	1.29
20	10.534 5	10.667 2	1.26

下载: 导出CSV

表 3 优化前后二自由度微动平台等效刚度对比

Table 3. Comparison of equivalent stiffness of 2-DOF micro-positioning stage before and after optimization

等效刚度/(N·m^-1)		优化率/%
优化前	优化后	优化率/%
1.907×10⁷	2.116×10⁷	10.96

下载: 导出CSV

表 4 二自由度微动平台前5阶固有频率仿真值

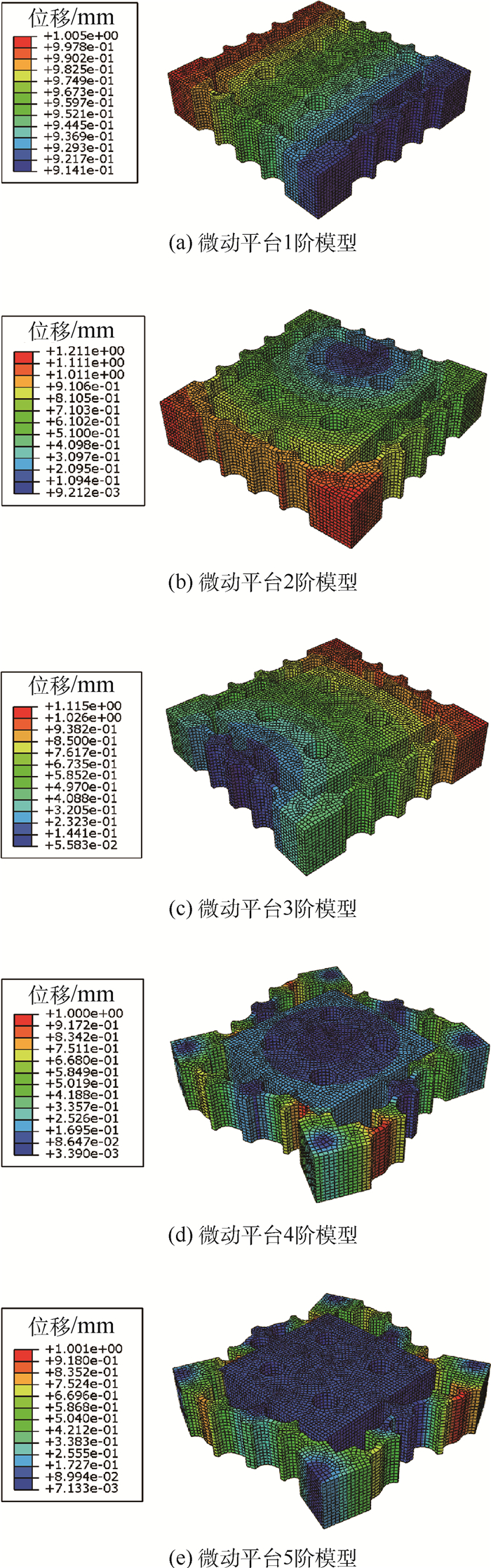
Table 4. The first five natural frequency simulation values of 2-DOF micro-positioning stage

阶数	固有频率仿真值/Hz
1阶	116.04
2阶	160.94
3阶	232.65
4阶	284.39
5阶	358.20

下载: 导出CSV

参考文献(22)

[1]	LIU P B, YAN P, ZHANG Z, et al.Flexure hinges guided nano-stage for precision manipultions:Design, modeling and control[J].Precision Engineering and Manufacturing, 2015, 16(11):2245-2254. doi: 10.1007/s12541-015-0289-5
[2]	刘凯, 曹毅, 周睿, 等.二自由度平板折展柔性铰链的分析及优化[J].航空学报, 2016, 36(1):142-152. http://d.old.wanfangdata.com.cn/Periodical/hkxb201702028 LIU K, CAO Y, ZHOU R, et al.Analysis and optimization of a 2-DoF flexure hinge[J].Acta Aeronautica et Astronautica Sinica, 2016, 36(1):142-152(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hkxb201702028
[3]	CHOI E, KWON K, DAEJOONG K, et al.Tunable reverse electrodialysis with geometrically controlled self-assembled nanoparticle network[J].Lab on A Chip, 2015, 15(1):168-178. doi: 10.1039/C4LC01031K
[4]	马立, 谢炜, 刘波, 等.柔性铰链微定位平台的设计[J].光学精密工程, 2014, 22(2):338-345. http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201402014 MA L, XIE W, LIU B, et al.Design of flexible sources positioning platform[J].Optics and Precision Engineering, 2014, 22(2):338-345(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/gxjmgc201402014
[5]	王振华, 陈立国, 孙立宁.集成式6自由度微动并联机器人系统[J].光学精密工程, 2007, 15(9):1391-1397. doi: 10.3321/j.issn:1004-924x.2007.09.014 WANG Z H, CHEN L G, SUN L N.Integrated 6-DoF micro-motion parallel robot system[J].Optics and Precision Engineering, 2007, 15(9):1391-1397(in Chinese). doi: 10.3321/j.issn:1004-924x.2007.09.014
[6]	LAI L J, GU G Y, ZHU L M.Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage[J].Review of Scientific Instruments, 2012, 83(4):105-111. https://www.researchgate.net/publication/224912161_Design_and_control_of_a_decoupled_two_degree_of_freedom_translational_parallel_micro-positioning_stage
[7]	LI Y M, WU Z G.Design, analysis and simulation of a novel 3-DoF translational micro manipulator based on the PRB model[J].Mechanism and Machine Theory, 2016, 100(3):235-258. https://www.researchgate.net/publication/220103687_Design_analysis_and_stiffness_optimization_of_a_three_degree_of_freedom_parallel_manipulator
[8]	陶惠峰.超精密微位移系统研究[D].杭州: 浙江大学, 2003: 1-7. TAO H F.Research on ultra-precision micro displacement system[D].Hangzhou: Zhejiang University, 2003: 1-7(in Chinese).
[9]	刘庆玲, 翁海珊, 邱丽芳.新型单边直圆椭圆混合柔性铰链的柔度计算及其性能分析[J].工程力学, 2010, 27(10):52-56. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201002473014 LIU Q L, WENG H S, QIU L F.Flexibility calculation and performance analysis of a new Unilateral elliptical hybrid flexure hinge[J].Engineering Mechanics, 2010, 27(10):52-56(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201002473014
[10]	任宁, 田国豪, 欧开良, 等.倒圆角直梁型柔性铰链刚度研究[J].机械强度, 2012, 34(3):366-370. http://d.old.wanfangdata.com.cn/Periodical/jxqd201203010 REN N, TIAN G H, OU K L, et al.Study on the stiffness of inverted fillet flexible hinge[J].Mechanical Strength, 2012, 34(3):366-370(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jxqd201203010
[11]	BHAGAT U, SHIRINZADEH B, CLARK L, et al.Design and analysis of a novel flexure-based 3-DOF mechanism[J].Mechanism and Machine Theory, 2014, 74(2):173-187. https://www.sciencedirect.com/science/article/pii/S0094114X13002498
[12]	GUO Z L Tat J T, YANG G L, et al.Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism[J].Precision Engineering, 2015, 39(5):125-133. https://www.journals.elsevier.com/precision-engineering/most-cited-articles/
[13]	GAO P, SWEI S M, YUAN Z.A new piezodriven precision micropositioning stage utilizing flexure hinges[J].Nanoteehnology, 1999, 10(4), 394-398. doi: 10.1088/0957-4484/10/4/306
[14]	陈贵敏, 贾建援, 勾燕洁.混合型柔性铰链研究[J].仪器仪表学报, 2004, 25(4):110-112. http://d.old.wanfangdata.com.cn/Periodical/yqyb2004z3037 CHEN G M, JIA J Y, GOU Y J.Study on hybrid flexible hinge[J].Chinese Journal of Scientific Instrument, 2004, 25(4):110-112(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/yqyb2004z3037
[15]	沈剑英, 张海军, 赵云.压电陶瓷驱动器杠杆式柔性铰链机构放大率计算方法[J].农业机械学报, 2013, 44(9):267-271. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201309046 SHEN J Y, ZHANG H J, ZHAO Y.Calculation method of magnification of lever-type flexible hinge mechanism of piezoelectric ceramic actuator[J].Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(9):267-271(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201309046
[16]	LI Y M, XIAO S L, XI L Q, et al.Design, modeling, control and experiment for a 2-DOF compliant micro-motion stage[J].Precision Engineering and Manufacturing, 2014, 15(4):735-744. doi: 10.1007/s12541-014-0394-x
[17]	田延岭, 张大卫, 闫兵.二自由度微定位平台的研制[J].光学精密工程, 2006, 14(1):94-99. doi: 10.3321/j.issn:1004-924X.2006.01.017 TIAN Y L, ZHANG D W, YAN B.Development of 2-DOF micro positioning platform[J].Optics and Precision Engineering, 2006, 14(1):94-99(in Chinese). doi: 10.3321/j.issn:1004-924X.2006.01.017
[18]	崔玉国, 阮超, 马剑强, 等.2-DoF并联柔性结构微动平台的新构型及尺寸优化[J].机器人, 2016, 38(3):352-359. http://d.old.wanfangdata.com.cn/Periodical/jqr201603012 CUI Y G, RUAN C, MA J Q, et al.New configuration and dimension optimization of jogging parallel flexible structure platform[J].Robot, 2016, 38(3):352-359(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jqr201603012
[19]	李仕华, 韩雪艳, 马琦翔, 等.新型并联柔性铰链微动精密平台的研究[J].中国机械工程, 2016, 27(7):888-893. doi: 10.3969/j.issn.1004-132X.2016.07.007 LI S H, HAN X Y, MA Q X, et al.Research on jogging precision platform of new type of parallel flexible hinge[J].China Mechanical Engineering, 2016, 27(7):888-893(in Chinese). doi: 10.3969/j.issn.1004-132X.2016.07.007
[20]	徐刚, 瞿金平, 杨智韬.一种改进的自适应粒子群优化算法[J].华南理工大学学报, 2008, 36(9):6-10. doi: 10.3321/j.issn:1000-565X.2008.09.002 XU G, QU J P, YANG Z T.An improved self-adaptive particle swarm optimization algorithm[J].Journal of South China University of Technology, 2008, 36(9):6-10(in Chinese). doi: 10.3321/j.issn:1000-565X.2008.09.002
[21]	李宝磊, 施心陵, 苟常兴, 等.多元优化算法及其收敛性分析[J].自动化学报, 2015, 41(5):949-959. http://d.old.wanfangdata.com.cn/Periodical/zdhxb201505009 LI B L, SHI X L, GOU C X, et al.Multivariate optimization algorithm and its convergence analysis[J].Acta Automatica Sinica, 2015, 41(5):949-959(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/zdhxb201505009
[22]	郭明陆.压电陶瓷驱动的微纳定位平台系统研究[D].沈阳: 东北大学, 2014: 21-35. GUO M L.Study on micro-nano positioning platform driven by piezoelectric ceramics[D].Shenyang: Northeastern University, 2014: 21-35(in Chinese).