Effect of flow stress calculation on formability of aluminum alloy warm sheet hydroforming
-
摘要:
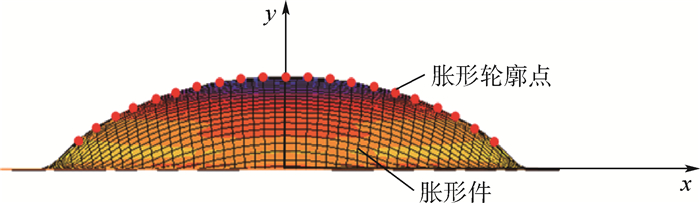
为研究流动应力计算对铝合金板材充液热成形性能的影响,进行了板材热态胀形试验,得到了不同直径的胀形高度-压力曲线。结合三坐标测量仪测得的胀形零件轮廓数据,拟合出了最小二乘圆(LSCF)半径,发现在高径比(
h /a )范围(0.18 <h /a ≤0.68)内,对应的曲率半径与圆形半径之间的圆形度误差为5%。为获取更为精确的应力-应变曲线,通过对现有曲率半径和厚度理论模型进行比较,结合流动应力计算,发现Hill及Panknin曲率半径模型的平均值及Kruglov-Hill厚度模型最符合试验数据。利用组合模型计算胀形试验所得到的胀形高度-压力曲线,得到了不同温度、不同压力率下的应力-应变曲线。结果表明,210℃时方向异性(轧制方向及垂直方向)对铝合金7075-O胀形件曲率半径的影响很小;同时,压力率可影响其应力-应变曲线。Abstract:In order to research the influence of flow stress calculation on formability of aluminum alloy warm sheet hydroforming, warm sheet bulging test was carried out to obtain bulging height-pressure curves with different bulging diameters in this study. Based on the data of bulging parts profile measured by three coordinate measuring machine, the least square circle fit (LSCF) radius were fitted, and it was found that when the height-diameter ratio
h /a was in the range of 0.18 <h /a ≤ 0.68, the corresponding value of roundness error between the radius of curvature and the circle radius was 5%. By comparing the existing theoretical models for radius of curvature and thickness, which is combined with flow stress calculation, it was found that the average value of radius of curvature model Hill and Panknin, and the thickness model Kruglov-Hill are in the most accordance with experimental data. The combination model was used to calculate the bulging height-pressure curves obtained by bulging test, and then the stress-strain curves with different temperatures and pressure rates were obtained. It was found that there was a little impact on radius of curvature for different directions (rolling direction and vertical direction) of the bulging parts formed with 7075-O aluminum alloy at 210℃, while the pressure rate can affect the stress-strain curves.-
Key words:
- warm sheet hydroforming /
- flow stress /
- formability /
- stress-strain curve /
- pressure rate
-
成分 Zn Mg Cu Mn Cr Fe Si Ti 其他 Al 含量/% 5.1 2.1 1.2 0.3 0.18 0.5 0.4 0.2 0.2 余量 表 2 不同胀形高度时试验测量数据和有限元拟合数据胀形件轮廓最小二乘圆半径对比
Table 2. Comparison of LSCF radius of bulging parts profile based on experimental measurment data and finite element fitting data with different bulging heights
mm 胀形高度 轧制方向 垂直方向 有限元拟合最小二乘圆半径 圆心(y, z) 最小二乘圆半径 圆心(x, z) 最小二乘圆半径 10 (-94.73, -159.32) 107.16 (108.77, -160.12) 107.95 103.77 12 (-91.72, -133.30) 84.18 (113.19, -133.25) 84.13 83.75 16 (-97.33, -114.89) 68.79 (117.74, -114.77) 68.66 67.79 20 (-91.99, -94.10) 53.70 (117.51, -94.30) 53.90 55.15 22 (-92.85, -91.94) 52.35 (120.50, -91.92) 52.32 52.14 表 3 不同顶点曲率半径及顶点厚度解析模型
Table 3. Analytical model for different vertex radius of curvature and vertex thickness
顶点曲率半径 顶点厚度 模型 表达式 模型 表达式 Hill 
Jovane 
Panknin 
Hill 
Kruglov 
注:rc—胀形半径; hd—胀形高度; rf—胀形圆角半径; t(td)—顶点厚度; t0—板材初始厚度。 表 4 胀形高度-压力曲线5次多项式拟合
Table 4. Five-order polynomial fitting of bulging height-pressure curves
温度 压力率/(MPa·s-1) 5次多项式拟合 A0 A1 A2 A3 A4 A5 常温 0.05 0.003 -0.011 0.068 -0.005 1.94×10-4 -3.19×10-6 0.005 -0.022 -0.014 0.061 -0.004 8.73×10-5 -7.88×10-7 160℃ 0.05 -0.044 0.092 0.029 -0.003 1.08×10-4 -2.05×10-6 0.005 0.013 -0.027 0.034 -0.002 4.92×10-5 -5.29×10-7 210℃ 0.05 0.001 0.080 0.018 -0.001 6.23×10-5 -1.09×10-6 0.005 -0.038 0.116 0.002 6.23×10-5 -9.21×10-6 1.52×10-7 280℃ 0.05 -0.015 0.065 0.011 -9.99×10-4 4.69×10-5 -8.76×10-7 0.005 -0.013 0.046 0.006 -4.22×10-4 1.55×10-5 -2.25×10-7 -
[1] SELLARS C M, MCTEGART W J.On the mechanism of hot deformation[J].Acta Metallurgica, 1966, 14(9):1136-1138. doi: 10.1016/0001-6160(66)90207-0 [2] HOULSBY G T, PUZRIN A M.Principles of hyperplasticity[M].London:Springer-Verlag, 2006:19-28. [3] KOC M, BILLUR E, CORA O N.An experimental study on the comparative assessment of hydraulic bulge test analysis methods[J].Materials and Design, 2011, 32(1):272-281. doi: 10.1016/j.matdes.2010.05.057 [4] LANG L H, CAI G S, LIU K N, et al.Investigation on the effect of through thickness normal stress on forming limit at elevated temperature by using modified M-K model[J].International Journal of Material Forming, 2015, 8(2):211-228. doi: 10.1007/s12289-014-1161-3 [5] NURCHESHMEH M, GREEN D E.Influence of out-of-plane compression stress on limit strains in sheet metals[J].International Journal of Material Forming, 2012, 5(3):213-226. doi: 10.1007/s12289-011-1044-9 [6] LANG L H, LIU B S, LI T, et al.Experimental investigation on hydromechanical deep drawing of aluminum alloy with heated media[J].Steel Research International, 2012, 83(3):230-237. doi: 10.1002/srin.v83.3 [7] 马高山.5A90铝锂合金板材热成形有限元模拟与试验研究[D].北京: 北京航空航天大学, 2008: 37-46.MA G S.FEM simulation and experimental research on hot forming of 5A90 Al-Li alloy sheet[D].Beijing: Beihang University, 2008: 37-46(in Chinese). [8] LIU B S, LANG L H, ZENG Y S, et al.Forming characteristic of sheet hydroforming under the influence of through-thickness normal stress[J].Journal of Materials Processing Technology, 2012, 212(9):1875-1884. doi: 10.1016/j.jmatprotec.2012.03.021 [9] HOFFMANNER A L.Development of workability testing techniques: F33615-67-C-1466[R].Cleveland: Interim Report on Air Force Contract, 1967. [10] GROCHE P, HUBER R, DOERR J, et al.Hydromechanical deep-drawing of aluminium-alloys at elevated temperatures[J].CIRP Annals, 2002, 51(1):215-218. doi: 10.1016/S0007-8506(07)61502-9 [11] KAYA S, ALTAN T, GROCHE P, et al.Determination of the flow stress of magnesium Az31-O sheet at elevated temperatures using the hydraulic bulge test[J].International Journal of Machine Tools and Manufacture, 2008, 48(5):550-557. doi: 10.1016/j.ijmachtools.2007.06.011 [12] MAHABUNPHACHAI S, KOC M.Investigations on forming of aluminum 5052 and 6061 sheet alloys at warm temperatures[J].Materials and Design, 2010, 31(5):2422-2434. doi: 10.1016/j.matdes.2009.11.053 [13] LANG L H, WANG Z R, KANG D C, et al.Hydroforming highlights:Sheet hydroforming and tube hydroforming[J].Journal of Materials Processing Technology, 2004, 151(1-3):165-177. doi: 10.1016/j.jmatprotec.2004.04.032 [14] SIEGERT K, JAGER S, VULCAN M.Pneumatic bulging of magnesium AZ 31 sheet metals at elevated temperatures[J].CIRP Annals, 2003, 52(1):241-244. doi: 10.1016/S0007-8506(07)60575-7 [15] STRANO M, ALTAN T.An inverse energy approach to determine the flow stress of tubular materials for hydroforming applications[J].Journal of Materials Processing Technology, 2004, 146(1):92-96. doi: 10.1016/j.jmatprotec.2003.07.016 [16] 刘宝胜.板材充液热成形机理及关键技术研究[D].北京: 北京航空航天大学, 2012: 95-105.LIU B S.Research on forming mechanism and key technologies of warm sheet hydroforming[D].Beijing: Beihang University, 2012: 95-105(in Chinese). [17] GOTOH M, CHUNG T, IWATA N.Effect of out-of-plane stress on the forming limit strain of sheet metals[J].JSME International Journal Series A:Mechanics and Material Engineering, 1995, 38(1):123-132. doi: 10.1299/jsmea1993.38.1_123 [18] GUTSCHER G, WU H C, NGAILE G.Determination of flow stress for sheet metal forming using the viscous pressure bulge (VPB) test[J].Journal of Materials Processing Technology, 2004, 146(1):1-7. doi: 10.1016/S0924-0136(03)00838-0 [19] PRATT V.Direct least-squares fitting of algebraic surfaces[J].Computer Graphics, 1987, 21(4):145-152. doi: 10.1145/37402 [20] PEIRS J, VERLEYSEN P, VAN PAEPEGEM W, et al.Determining the stress-strain behaviour at large strains from high strain rate tensile and shear experiments[J].International Journal of Impact Engineering, 2011, 38(5):406-415. doi: 10.1016/j.ijimpeng.2011.01.004 [21] LANG L H, DU P M, LIU B S, et al.Pressure rate controlled unified constitutive equations based on microstructure evolution for warm hydroforming[J].Journal of Alloys and Compounds, 2013, 574:41-48. doi: 10.1016/j.jallcom.2013.03.134 -







 下载:
下载: