由于很难获取目标运动的先验信息，仅采用单模型的跟踪算法在不同机动情形下的跟踪效果往往较差。为了解决这个问题，多模型(Multiple Model, MM)算法^[1]得到了深入研究并被广泛应用于目标跟踪^[2-3]和轨迹预测^[4]等领域。MM算法的核心在于假设模型集包含目标所有可能运动模式的基础上，利用可能模型的概率加权匹配目标运动。MM算法的状态观测一般是模式依赖的，而且量测序列嵌入模式信息，即系统模式序列是Morkov过程。根据模型集设计方法，可以将MM算法分为固定结构和可变结构MM算法^[5]。其中，固定结构MM算法的代表是n阶广义伪贝叶斯(n-order Generalized Pseudo-Bayesian, GPBn)算法^[6]和交互多模型(Interacting Multiple Model, IMM)算法^[7]。IMM算法通过应用更好的假设管理技术，具有GPB2的性能和GPB1计算上的优势, 逐渐成为研究热点。针对固定结构MM算法高度依赖模型集和模型竞争导致的性能下降等问题^[8]，可变结构MM算法^[9-10]通过模型集自适应算法的开发具有较好的跟踪性能和费效比。

IMM算法是在GPB算法的基础上提出的一种具有系统模式Morkov切换的算法。IMM算法进行目标状态估计的计算时，考虑每个模型滤波器都有可能成为当前有效的系统模型滤波器，每个滤波器的初始条件都是基于前一时刻各条件模型滤波器结果的合成，即模型条件重初始化。由于合成过程中存在非等维状态向量的混合，例如当匀速(Constant Velocity, CV)模型和匀加速(Constant Acceleration, CA)模型进行混合估计时，加速度分量即为“额外”分量，而标准IMM算法并未给出关于此问题的描述。IMM混合估计需要匹配状态向量的前两阶矩(均值和协方差)，因此低维状态向量需要扩维以匹配高维状态向量，这也是本文讨论的主题。然而，目前此问题只有少量的研究^[11-14]。一种简单的方法^[11]是对低维状态采用零均值和方差进行扩维，但会导致有偏估计。文献[12, 14]提出了一种无偏方法，即利用高维状态中的均值和协方差对低维状态进行扩维。该方法通过弹道导弹数据进行了检验并展现了良好的性能。文献[13]认为被扩维的分布应该尽可能反映系统潜在情况(模式切换)，采用均匀分布描述“额外”分量，因而提高了模式切换时的跟踪精度。

本文所提方法基于以下思想：当前时刻的最优混合方法应根据时变的目标状态进行动态调整。本文方法在分析现有方法的基础上，将“切换”状态的概念引入目标状态，并利用模型概率和滤波新息进行联合判决，从而选择最优的混合方法，提高跟踪精度。

1.   问题描述

对于一个跳变线性系统，其数学描述为

式中:x_k和z_k分别为k时刻的状态向量和量测；F^j、H^j和G^j分别为模型j的状态转移矩阵、量测矩阵和噪声分布矩阵；w_k^j~和v_k^j~是互相独立的过程噪声和量测噪声序列, Q_k^j和R_k^j分别为过程噪声和量测噪声协方差。根据贝叶斯全概率理论，固定模型集的最优估计是全假设树估计，但所需计算资源难以满足^[8]。因此，IMM算法利用GPB算法进行系统估计时只考虑过去2个采样间隔内的历史，并认为系统模式是一阶齐次Markov链，其转移概率为

式中：Φ表示模型集；m_k^j表示k时刻模型j与系统真实模式匹配。为描述简便起见，假设模型集M只包含2个非等维状态的模型。事实上，本文算法容易推广到包含任意多个模型的模型集。

假设k时刻状态估计的后验概率是高斯分布的，即

式中:和P_kⁱ分别为系统模式为m_kⁱ时的均值和协方差估计；Z^k为从初始时刻到k时刻的量测序列集合。与其他MM算法不同，IMM算法在重初始化时考虑到前一时刻模型输出成为当前模型输入的可能性，即通过后向混合概率重初始化状态和协方差。后向混合概率计算式为

式中：μ_k^{i, j}为在给定k+1时刻模式为j时，k时刻模型为i的概率；μ_kⁱ为k时刻模型i概率；c_j为归一化因子。混合估计的状态估计及协方差为

假设模型1状态向量的维度高于模型2，即n_x¹>n_x²，且模型2的状态分量包含于模型1，即

式中:c_k为模型1和2的公共分量；为模型1的“额外”分量，在实践应用中可以是加速度、转弯率或推力等。由于模型的状态向量维度不均等，难以按照式(7)和式(8)实现混合估计。对于模型2的重初始化，可以舍弃“额外”分量，直接利用和进行，即

然而，对于模型1的重初始化，低维的状态向量必须按照某种方法进行扩维，这也正是本文所考虑的问题。

IMM算法是递推的，包括模型条件重初始化、模型条件滤波、模型概率更新和估计融合。其中，式(5)~式(8)给出了模型条件重初始化。

模型条件滤波是在给定重初始化的状态和协方差条件后进行状态估计更新，包含以下步骤：

1) 状态预测及协方差，计算式分别为

2) 新息(滤波残差)及其协方差，计算式分别为

3) 滤波更新，包括滤波增益、状态估计更新及其协方差，计算式分别为

模型概率更新，计算式分别为

式中:Λ_k+1ⁱ为与m_k+1ⁱ匹配的似然函数，服从高斯分布。

估计融合给出k+1时刻的总体估计及其协方差，计算式分别为

2.   非等维状态混合估计

如第1节所述，本文所研究的焦点是如何将“额外”分量体现到扩维后的状态向量上。假设模型2扩维后的状态x_k^{2, a}分布为

式中：q(e_k²)为模型2中“额外”分量e_k的分布。显然，不同混合方法的区别在于q(e_k²)的选择。本文总结了关于此问题以往的研究^[11-14]，下面介绍现有的3种方法，分别记为A₁，A₂和A₃。

1) A₁采取了一种简单的策略，认为由于e_k是模型1的分量并不存在于模型2，故可以用零均值和协方差进行扩维，则相应的分布q(e_k²)和扩维后的状态x_k^{2, a}为

式中：δ为冲激函数。

2) 文献[12, 14]提出了一种无偏方法A₂，认为A₁会导致模型1状态估计有偏，而e_k²利用模型1的“额外”分量e_k信息进行扩维是无偏的，相应的分布q(e_k²)和扩维后的状态x_k^{2, a}为

3) A₃考虑到系统模式切换的可能性，认为e_k²在其取值区间内服从均匀分布，则相应的分布q(e_k²)和扩维后的状态x_k^{2, a}为

式中:n_e=n_x¹-n_x²为e_k的维度；参数e_l取值区间为[a_l, b_l]；Cov(e_k²)表示e_k²的协方差。

事实上，上述3种方法是基于不同假设下设计的。A₁假设系统模式为m_k²，因此将“额外”分量e_k置零；A₂假设系统模式为m_k¹，因此e_k²直接利用e_k¹信息作为其分布；A₃假设系统模式可能切换，因此认为e_k²为均匀分布。显然，在假设成立的条件下，这些算法能够有效提高估计精度，但跳变线形系统的模式是互相转换的，也就是说目标的运动模式是时变的，在没有先验的情况下假设模式固定是不合理的。因此，本文提出方法的核心在于认为更为合理的混合估计方法应当基于目标当前状态而决定。为了实现对目标状态的准确估计，本文引入“切换”状态的概念。对于一个两模型交互的系统，目标状态包括S₁、S_1→2、S₂和S_2→1。显然，如果目标真实状态是已知的，则可以选择最佳的混合估计方法。假设目标真实状态为S₁，则q(e_k²)的最优选择为

同样地，当目标真实模式为S₂时，q(e_k²)的最优选择为

对于“切换”状态S_1→2，由于在此过程中e_k应置零，因此q(e_k²)的最优选择同式(32)。当目标状态为S_2→1时，意味着e_k可能在其取值区间跳变，q(e_k²)的分布应体现出此特性，故采用A₃的均匀分布假设，即

基于上述分析，可以发现A₁、A₂和A₃分别是不同目标状态下的最优方法。因此，在已知目标状态时，3种方法可以被纳入一个统一的框架，根据当前状态选择最优的一个。然而，跟踪系统很难准确知道目标的真实状态。尽管如此，依然可以利用一些滤波信息，例如模型概率和新息，尽可能地确定目标状态。

相比于状态S₁和S₂可以通过模型概率μ_kⁱ体现，“切换”状态由于模式切换导致的机动，往往体现在新息变化上。因此，为了检测“切换”状态S_2→1，本文采用一种常用于目标跟踪的机动检测器^[15-17]来确定目标当前状态。显然，当目标从模式2切换到模式1时，由于模型失配将导致模型2的新息增大。因此，令检验统计量为新息的衰减记忆平均值，计算式为

式中:ρ(s)=(1-λ)/(1-λ^s+1)，0＜λ < 1为衰减因子; v_k²和S_k²分别为模型2的新息及其协方差; s为滑窗长度; [k-s+1, k]为滑窗检测区间。在高斯假设下，由于v_k²和S_k²都服从零均值的高斯分布，故(v_k²)^T(S_k²)^-1v_k²服从自由度为n_z(量测向量维度)的卡方分布。作为一个独立同分布的高斯变量加权和，检验统计量ε_k虽然不是标准的卡方分布，但可以通过矩匹配被视作一个经过缩放的卡方变量^[16-17]，有

因此，检验统计量ε_k服从自由度为n_z的卡方分布。令假设H₀代表目标状态切换未发生，假设H₁则代表模型切换发生，“切换”状态S_2→1由式(36)检测：

由式(36)可知，当ε_k超过检测阈值χ²_nz(α)时拒绝假设H₀，否则接受该假设。由概率论可知，虚警概率P_fa=α，即在目标状态未改变的情况下错误判定目标状态发生变化的概率为α。因此，置信水平1-α通常设的相当高(例如95%或99%)以降低虚警概率。当检测门限χ²_nz(α)过高时，必然导致漏警概率P_la增大，即在目标状态已改变的情况下未成功检测。很显然，检测器往往需要在虚警概率和检测概率间做性能平衡，尽量降低误判造成的影响。

当检测器触发阈值，则状态S_2→1被激活，利用A₃重新估计滑窗区间[k-s+1, k]内的目标状态估计。当检验统计量ε_k低于式(36)阈值时，则直接利用模型概率确定目标状态，即

当μ_k¹>μ_k²时，认为目标状态为S₁，故采用A₂进行混合估计；否则认为目标状态为S₂，采取A₁。图 1给出了本文方法(记为A₄)的具体流程。

图  1  本文方法原理框图

Figure  1.  Functional block diagram of proposed method

下载: 全尺寸图片 幻灯片

如前所述，由于门限检测导致的一定的虚警及漏警。下面简要分析各种情况下A₄的跟踪性能差异。当目标真实状态未发生变化(H₀)，则正确接受H₀时的跟踪精度趋近于A₁或A₂，否则虚警导致A₄的跟踪精度趋近于A₃。当目标真实状态发生变化(H₁)，若正确接纳H₁，A₄则采用A₃重新估计[k-s+1, k]区间的状态，其跟踪性能趋近于A₃。相比于A₁和A₂，A₄能够在成功检测到状态变化后再启用A₃，这意味着A₄可以利用量测数据的后验信息来校正目标状态，从而抑制因模型切换造成的跟踪误差剧增，极大地降低峰值误差，其作用类似于IMM平滑器^[18]，区别在于前者只在检测器触发时作用。若错误地拒绝接纳H₁，由于漏警发生会导致跟踪误差增大，跟踪性能接近A₁或A₂。此外，滑窗长度s的选取同样影响跟踪性能。若滑窗过长会导致检测延迟，不利于系统快速响应模式切换；滑窗过短则导致检测的可靠性降低。因此，在虚警率较低的条件下尽可能地选择相对较短的滑窗长度以快速响应系统模式切换，具体设置方法可参考文献[15-16]。

基于上述分析可以看出，本文方法并不固定采用某种混合方法，而是通过新息检验和模型概率确定目标状态以选取最佳方法，从而将3种混合方法的优势结合起来。

3.   仿真与分析

在本节中，对由不同运动模型组成的运动场景进行了仿真实验，用于比较本文所提方法和现有3种方法的性能。在仿真中，本文考虑了过程噪声的影响，并给出2种评价指标，最后还讨论了仿真结果。

3.1   轨迹与模型

场景1：由2个常见的线形运动模型组成。其中，模型1和模型2分别为CA和CV模型，用于产生一个2D运动轨迹(即n_z=2)。2种运动模型的状态向量分别为

式中:x_k和y_k为位置分量；和为速度分量；和为加速度分量，即“额外”分量e_k。CA和CV模型的状态转移矩阵、量测矩阵和噪声分布矩阵分别为

式中:I₂表示2阶单位矩阵; T=1 s为采样间隔。

场景2：由线形的CV模型和非线性的协同转弯(Coordinated Turn, CT)模型组成。CT模型的相应参数设置为

式中:ω_k为转弯率。

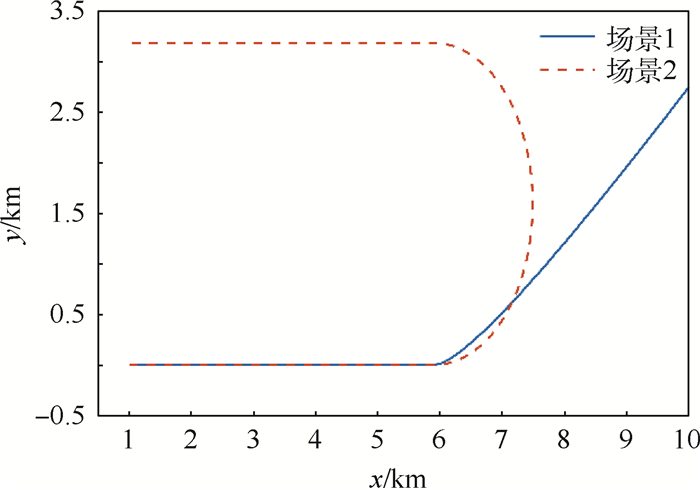
目标初始状态为[1 000 m 0 m 100 m/s0 m/s]^T。在0~50 s和101~150 s内做匀速运动，在51~100 s内，场景1目标做加速度为30 m/s²的匀加速运动，场景2做转弯率3.6 (°)/s的匀速转弯运动。目标的真实轨迹如图 2所示。

图  2  场景1和2的真实轨迹

Figure  2.  True trajectories of Scenarios 1 and 2

下载: 全尺寸图片 幻灯片

3.2   IMM参数设置与性能评价指标

对于上述2个场景，系统量测噪声方差为σ_m²=50² m²，其协方差为R_kⁱ=σ_m²I₂；过程噪声协方差为Q_kⁱ=σ_a²I₂，考虑到过程噪声的大小对跟踪性能的影响，故设为

除了混合方法之外，4种方法的IMM估计器参数设置是相同的，滤波算法采用卡尔曼滤波^[19]。A₁和A₂的原理在第2节已介绍过。由于A₃认为“额外”分量e_k服从均匀分布，式(29)中场景1的加速度的取值范围为[-100, 100]m/s²，场景2中转弯率取值范围为[-3.6, 3.6](°)/s。对于A₄，所需参数设置如下：衰减因子λ=0.95，置信度α=0.01；滑窗长度s=2，阈值χ₂²(α)=9.21。系统模式的Markov转移矩阵和初始模型概率分别为

本文的性能评价指标如下:

式中:M=500为蒙特卡罗仿真次数；N=150为目标运动时间；τ_k(σ_a)是过程噪声方差为σ_a²时的均方根误差(Root Mean Square Error, RMSE)；τ^σ_a为不同σ_a下的RMSE均值。

3.3   结果与分析

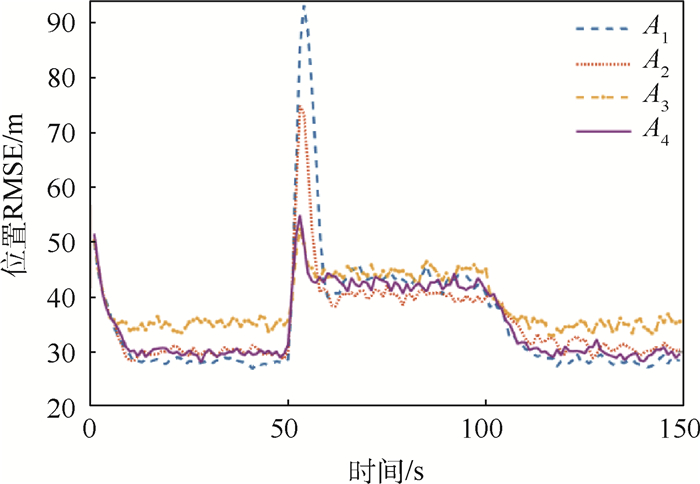
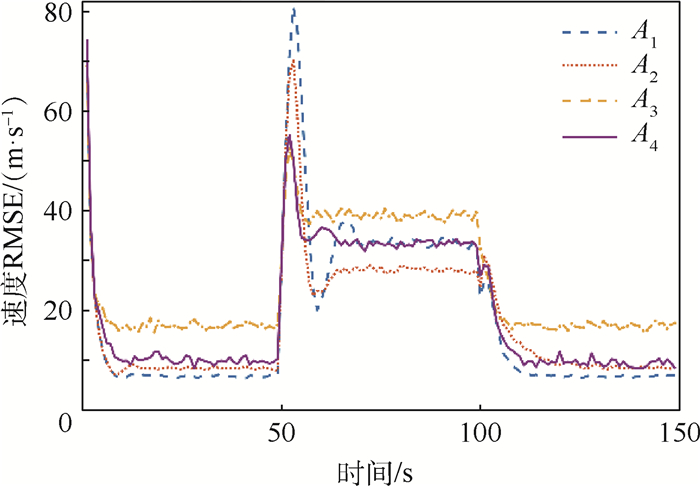
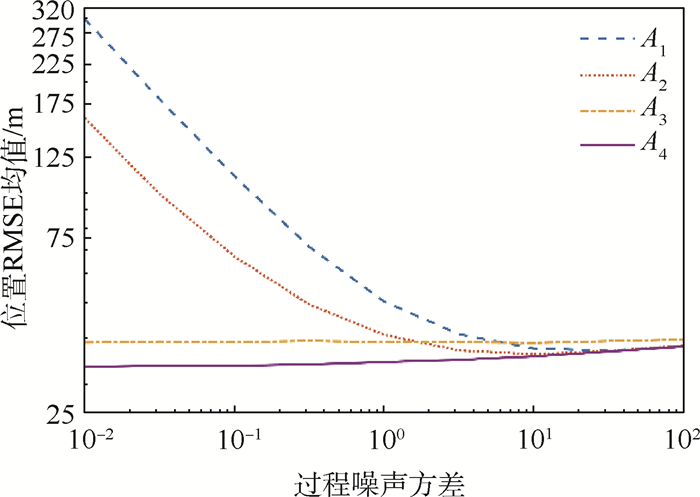
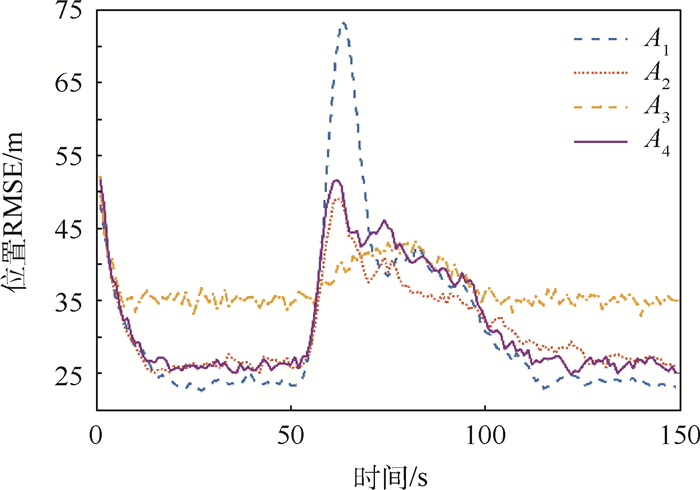
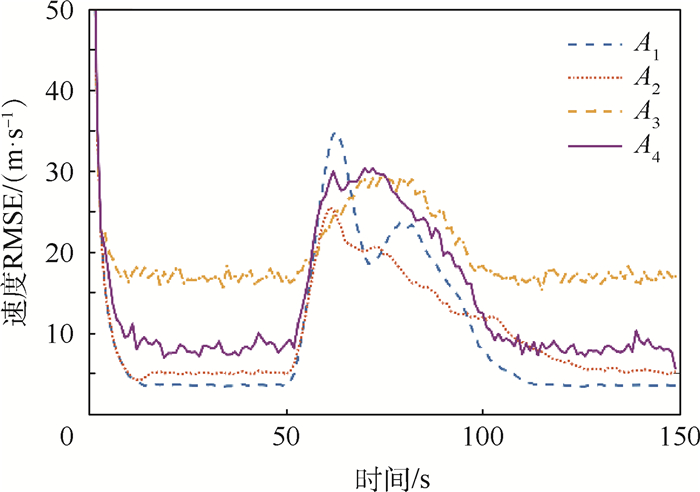
限于篇幅，本文只选择展示仿真结果中的一部分内容，但这并不影响4种算法间的性能比较。对于场景1来说，图 3~图 6分别展示了过程噪声方差σ_a²为10^-2和10^-1时的位置RMSE以及速度RMSE。显然，A₁、A₂和A₄在目标进行CV和CA运动时性能良好，但系统模式从CV切换到CA时，前2种算法的跟踪误差会急剧增大。A₃和A₄则能在模型切换时保持较好的跟踪精度。但A₃的缺陷在于，当系统模式不发生切换时，它的跟踪精度是4种方法中最差的。随着过程噪声方差的增大，4种算法间的性能差别逐渐变小，这种趋势如图 7所示。同样地，对于场景2，图 8和图 9给出了过程噪声方差σ_a²为10⁰时的位置RMSE以及速度RMSE。图 10给出了不同过程噪声方差时的位置RMSE均值，容易看到场景2的仿真结果类似于场景1。

图  3  场景1位置均方根误差(σ_a²=10^-2)

Figure  3.  Position RMSE of Scenario 1 (σ_a²=10^-2)

下载: 全尺寸图片 幻灯片

图  4  场景1速度均方根误差(σ_a²=10^-2)

Figure  4.  Velocity RMSE of Scenario 1 (σ_a²=10^-2)

下载: 全尺寸图片 幻灯片

图  5  场景1位置均方根误差(σ_a²=10¹)

Figure  5.  Position RMSE of Scenario 1 (σ_a²=10¹)

下载: 全尺寸图片 幻灯片

图  6  场景1速度均方根误差(σ_a²=10¹)

Figure  6.  Velocity RMSE of Scenario 1 (σ_a²=10¹)

下载: 全尺寸图片 幻灯片

图  7  不同过程噪声下场景1位置均方根误差均值

Figure  7.  Mean value of position RMSE of Scenario 1 under different process noises

下载: 全尺寸图片 幻灯片

图  8  场景2位置均方根误差(σ_a²=10⁰)

Figure  8.  Position RMSE of Scenario 2 (σ_a²=10⁰)

下载: 全尺寸图片 幻灯片

图  9  场景2速度均方根误差(σ_a²=10⁰)

Figure  9.  Velocity RMSE of Scenario 2 (σ_a²=10⁰)

下载: 全尺寸图片 幻灯片

图  10  不同过程噪声下场景2位置均方根误差均值

Figure  10.  Mean value of position RMSE of Scenario 2 under different process noises

下载: 全尺寸图片 幻灯片

由仿真结果可见，无论目标处于何种状态或过程噪声，A₄都能保持较好的性能，因此本文所提算法A₄的性能要优于其他3种算法。基于上述仿真结果，本文总结如下：

1) 过程噪声对不同混合方法有显著影响。当过程噪声较小时，系统模式切换导致的机动要求增大“额外”分量的协方差，这可以通过q(e_k²)的设计实现。

2) 实际上，A₃采用的均匀分布始终保持一个较大的协方差，因此对模型切换时的跟踪误差抑制起到了较好的作用，但相比于A₁和A₂所采取的策略，A₃牺牲了目标状态处于稳态时的跟踪精度。

3) A₄性能优越的原因在于，通过对目标状态的重新划分，并利用检测器对目标状态进行确认可以灵活地调整当前混合方法，使其具有了3种方法的优势。

4) 当过程噪声较大时，其协方差已足够大导致各方法间的差异逐渐消失。

4.   结论

本文提出了一种基于非等维状态的IMM混合估计方法，通过仿真结果验证了该方法具有良好的性能，得出以下结论：

1) 过程噪声的大小会影响IMM混合方法的性能，较小的过程方差会导致较大的模型切换误差，而较大的过程噪声方差会削弱这种影响。

2) 通过引入“切换”状态实现目标状态的重新划分，结合滤波信息可以实现对目标状态的确定，从而灵活地选取当前最佳的混合方法。

为使本文提出的算法能具有更好的适应性，仍需要对目标状态确认逻辑做更为深入理论分析。