Reliability evaluation of tank under uncertain conditions based on interval convex model
-
摘要:
针对不确定条件下液体推进剂贮箱的可靠性评估问题，基于贮箱应力强度与区间凸模型理论，确立了贮箱应力强度可靠性评估方法。首先，在液体推进剂贮箱数学模型的基础上，分析推导了贮箱的应力分布，结合应力强度理论，确定了贮箱的等效应力。其次，结合应力强度干涉理论及正则化区间面积比方法，定义了贮箱的应力强度区间凸模型可靠性指标。最后，结合某型火箭推进剂贮箱的实际参数，将贮箱等效应力与临界应力的不确定性转化为区间凸集形式进行了实例验证，并与椭球凸模型可靠性指标结果进行了对比。结果表明：应力强度区间凸模型可靠性指标可准确评估贮箱的完全可靠状态，并可将贮箱非完全可靠状态下的可靠度量化到[0, 1]区间。
Abstract:Aimed at the reliability evaluation problem of liquid propellant tank under uncertain conditions, the reliability evaluation method of tank stress strength is established based on tank stress strength and interval convex model theory. Firstly, the stress distribution of propellant tank is analyzed and derived based on the liquid propellant tank mathematical model, and the equivalent stress is confirmed through combining with the stress strength theory. Secondly, based on the stress strength interference theory and the area ratio of regularized interval theory, the interval convex model reliability index of tank stress strength is defined. Finally, combined with the actual parameters of a certain type rocket propellant tank, the method is verified through transforming the equivalent stress and critical stress into interval convex set form, and then it is compared with the reliability index results of ellipsoid convex model. The results show that the stress intensity interval convex model reliability index can evaluate the tank's entirely reliable states accurately, and can quantize the reliability degree of tank's non-entirely reliable states into the interval of [0, 1].
-
Key words:
- propellant tank /
- uncertain conditions /
- reliability /
- stress strength /
- interval convex model
-
傅里叶变换、小波变换、奇异值分解等方法在信号处理领域中得到了广泛的应用与发展[1]，与此同时，信号的稀疏表示理论也逐渐成为研究热点，在信号去噪[2]、数据压缩[3]、盲源分离以及特征提取等领域都有应用。傅里叶变换以及小波变换中的信号表示是基于正交基的，因此需要保证基函数系的完备性和正交性，保证固有最小分辨率的存在性，这使得正交分解有了约束和局限性。然而，稀疏分解从信号自身特点出发，针对性地选择相应的基函数，目的是用尽可能少的基函数来表示原信号，方法较灵活、适应性强[4-7]。
电磁兼容性是电子信息系统以及电路系统的重要性能，是电子电路系统具备电磁环境适应能力的基础和前提[8]。电路系统中对设备性能及响应测试中常常需要注入指定形式的信号，如正弦(sine)、方波(square)、正切(tangent)、脉冲(pulse)、三角波(triangular wave)等，以及由基本信号所组成的混合信号。不同的测试信号可实现不同的功能，如测量系统的频率特性、模拟测试雷达信号等。系统的响应常常会耦合到环境中的噪声，为更好地提取原始信号的特征，对设备进行评估或故障判定，首先需要对含噪信号进行降噪处理，因此，本文提出的对于电路系统中测试响应信号的基于梯度方向追踪的K奇异值分解(GP-KSVD)稀疏重构算法可作为对信号的预处理方法，为下一步对信号参数的特征提取分析提供了前提和基础。本文针对算法重构的有效性，结合常用的激励响应信号进行模拟仿真分析，并对电磁发射信号进行了实测验证。
稀疏分解是基于冗余过完备原子库的信号表示，给定冗余字典矩阵D，目标是找到信号的最稀疏表示，用数学语言描述为
(1) 式中：Γ为稀疏系数向量；l0范数||Γ||0表示向量Γ中非零元的个数，即稀疏度。
求解优化问题(1)，即是遍历字典矩阵D中原子的所有可能组合方式，找到能够表示信号的最稀疏组合。常用的实现方法包括用l1范数代替l0范数的凸优化方法，如基追踪(Basis Pursuit, BP)算法[9]和依赖于贪婪准则的近似逼近贪婪算法。其中经典的贪婪算法主要有匹配追踪(Matching Pursuit, MP)[10-12]、正交匹配追踪(Orthogonal Matching Pursuit, OMP)[13]算法等。OMP算法的复杂度体现在对字典矩阵的最小二乘运算上，且字典矩阵逐步扩充，导致算法的运算速度较慢。另外，BP算法在处理非严格稀疏的信号时，其运算复杂度更高[14]。
本文利用信号的稀疏性和可压缩性对信号进行稀疏表征去噪。首先结合原始训练信号进行字典学习，得到稀疏系数；进而对于含噪信号进行重构，实现去噪的目的。基于这一原理将贪婪算法中的梯度追踪(GP)算法与字典学习的K奇异值分解(KSVD)算法结合，实现电路系统测试响应信号的重构。
应用稀疏表征对信号去噪的主要关注点即为算法迭代的复杂度、计算机的储存消耗以及重构效果的好坏。在稀疏表征的几种贪婪算法中寻求迭代复杂度最低、计算机储存消耗也最低的方法就是本文的目的；另外，考虑到算法要能够对多种形式的信号均具有良好的重构去噪效果，则采用字典更新的算法，充分结合各种信号本身的特点，实现重构去噪效果好的目的。因此，基于以上需求以及分析，本文提出了GP-KSVD算法进行信号重构去噪。
电路系统中，对于待测设备进行性能评估以及故障诊断的研究，首先需要进行信号采样，而信号的采样和传输过程中，由于所绕制线圈的结构不对称、互感、引出线的旁路电容、外界地磁场等可能对采集数据造成误差。因此，对测试响应信号进行预处理，消除噪声对信号的干扰是十分必要的。
常用的去噪方法包括傅里叶变换、小波变换[15]、经验模式分解(EMD)[16]以及自适应滤波[17]等，小波变换以及小波分析由于其具有的良好的时频特性而被广泛应用，但小波基函数的选择对算法的实现效果有很大的制约；EMD方法在噪声水平较大且待滤波序列中具有高频信号时, 滤波曲线会出现明显失真现象。自适应滤波常用于处理实时信号，目的是去除谐波干扰，但易受到收敛因子的影响。本文选择的GP-KSVD算法依据信号本身数据特点更新字典，摆脱了字典基原子的选择受限问题；对于高频信号也具有较好的效果；针对测试响应信号采用的是稳态信号，且主要是去除环境噪声干扰，针对性强，应用效果明显。
稀疏表征方面，已有研究[18]中，应用OMP以及块正交匹配追踪(BOMP)算法结合KSVD算法对信号进行稀疏表征，但算法复杂度以及计算机存储消耗都比较高，且只适用于大规模的信号，存在局限性，本文在此基础上提出GP-KSVD算法，从算法复杂度到储存消耗再到各类型信号的处理上都得到了提升与改进，具有普遍适用性。
1. GP-KSVD算法原理分析
1.1 GP算法
Blumensath和Davies[19]提出共轭梯度追踪方法(CGP)，实质是利用共轭梯度方法求解OMP。依据对共轭方向的不同计算方法可得到不同的追踪方法，常见的有逼近共轭梯度追踪方法以及梯度追踪方法。其中，梯度追踪的目标是求最速下降法的最优解，首先要选择适当的搜索方向以及搜索步长，在获得较好重构效果的同时有效降低了算法的复杂度。
对于已知向量x∈RM，R为实数集合，矩阵D∈RM×N，满足M＜N，称D为N列向量原子Di组成的字典，稀疏表征就是寻找向量Γ满足关系式：
x=DΓ+ε
其中:ε为信号近似误差，ε≥0。
算法迭代过程中用Γn表示迭代n步后所选出的元素的指标集合，DΓn为由指标Γn中确定的原子所组成的字典的子集，追踪算法中的目标函数：
在迭代中稀疏系数向量Γ的更新用yΓnn表示，基于匹配追踪，方向更新为dΓn：
其中：an为方向更新步长。
GP算法实现步骤如下：
1) 初值设定：r0=x, y0=0，Γ0=∅。
2) 对于迭代步数n=1, n:=n+1, 直到满足迭代终止条件：
① gn=DTrn-1。
②
③ 下标集更新:Γn=Γn-1∪in。
④ 计算更新方向:dΓn。
⑤ cn=DΓndΓn。
⑥ 计算最优步长:an=＜rn, cn>/c2n2。
⑦ yΓnn:=yΓnn-1+andΓn。
⑧ rn=rn-1-ancn。
3) 输出rn、yn。
梯度追踪的梯度gn则是与稀疏系数yΓnn有关的gn=DT(x-DΓnyΓnn-1)。将该梯度作为追踪算法的更新方向，算法通过每步计算目标函数的负梯度方向和搜索步长，使目标函数沿负梯度方向以此步长搜索得到每步重构值的最优解，从而避免了OMP算法中的高维度最小二乘运算以及BP算法中求解凸优化问题所导致的运算复杂度高的缺点，梯度追踪算法能够降低运算复杂度，提高运算速度，同时依然能够保证估计效果[20-21]。
1.2 KSVD算法
对于稀疏表示，选择不同的冗余字典，信号重构的效果不同，常用的冗余字典包括随机字典、DCT字典、傅里叶基字典以及小波基字典等。为有效地训练一个用于信号稀疏表示的字典，Elad和Aharon[22]提出K奇异值分解算法，可同时更新当前原子和相应的稀疏系数，其创新在于不需要计算字典的逆矩阵，提高了运算速度。但是，KSVD的缺点在于算法得到的可能是局部最小值甚至是鞍点。
KSVD算法主要包括2个部分：
1) 在初始冗余字典D0=[d1, d2, …, dN]∈RM×N(N>M)下对信号训练集X=[x1, x2, …, xN]∈RM×N进行稀疏编码，本文选用了贪婪算法中的GP算法进行表示。
2) 基于稀疏系数矩阵Γ=[Γ1, Γ2, …, ΓN]∈RN×N，对字典的各列进行更新，且每次更新一列原子。对于由第j列原子表征的信号元素XI，原子更新满足重构误差项||XI-DΓI||F2尽可能最小的条件。目标函数近似表示为：{d, g}:=
KSVD算法步骤概括如下:
1) 输入：信号集X，初始化字典D0，目标稀疏度K，迭代次数n。
2) 输出：更新后字典D，稀疏系数矩阵Γ，使得X≈DΓ。
3) 令D=D0。
4) 矩阵D列归一化。
5) 迭代次数n=1, 2, …, k, 利用GP算法进行稀疏表示，即求解
6) 字典更新：对于j=1, 2, …, N，按列更新字典原子。
7) Dj:=0。
8) 下标集I:={用字典原子dj稀疏表示的信号X中的元素指标}。
9) 计算表示误差矩阵E：=XI-DΓI。
10) 利用目标函数求更新的原子以及稀疏系数：
11) Dj:=d。
12) Γj, I:=gT。
13) j循环结束。
14) n循环结束，迭代停止，得到更新字典D和稀疏矩阵Γ。
1.3 GP-KSVD算法及其复杂度
GP-KSVD算法是要充分利用GP算法复杂度低、计算时间短的优点，将测试响应信号进行梯度追踪表示，首先选取常用的初始字典，从内积最大的角度将含噪的信号表示成在各个主要方向上投影求和的形式，得到相应的稀疏系数；继而结合信号数据本身，将字典中的各列元素进行更新，基于矩阵的SVD分解原理，求解能够使得目标函数最小的字典列元素，实现字典学习、字典更新的目的。将GP与KSVD算法结合，从而更好地对测试响应信号进行重构去噪。
GP-KSVD具体算法步骤如下:
1) 初始设定：信号集X，初始化字典D0，目标稀疏度K，迭代次数k。
2) 稀疏表征：在初始字典D0利用GP算法进行稀疏表示，执行GP算法中的1) ~3) 步。其中关于y的梯度表达式可写为
其中：gΓn就是梯度追踪方法中的更新方向，信号集X中的各列元素分别作为r0，经过表征得到相应的稀疏系数yin, i=1, 2，…, N，从而得到γ=[y1n, y2n, …, yNn]。
3) 字典更新：令D=D0，执行KSVD算法中的6) ~14) 步。
4) 算法输出：得到GP-KSVD算法下的更新字典D, 稀疏系数矩阵Γ。
5) 将字典D代入GP算法中，对含噪信号进行稀疏重构表征，实现信号去噪。
算法的综合复杂度决定了计算机运算的储存消耗大小以及算法的运算速度。GP算法具有复杂度低的优点，这就决定了算法运行的计算机储存消耗较低，从而运算时间较短。
从理论角度进行分析，在l1范数的约束下，为精确重构稀疏度为K的信号，BP算法的运算复杂度约为O (N3)，且随着信号维度的增加而升高。OMP算法在每步迭代中都用最小二乘法计算，每步迭代的运算复杂度约为O (M2N)。在GP算法中，每步迭代都需要计算字典矩阵D中所有原子和当前信号残差rn-1的内积。字典矩阵D中共有N个原子，rn-1有M个值，则内积运算共MN次，因此，GP算法的运算复杂度约为O (MN)。具体来看，在GP算法的第1步中，要求出内积最大的原子，需要进行N次操作，算法中需要存储字典D，此外，还需存储的有残差r、系数向量yΓ、指标集Γn和内积向量gn，则相应的存储长度分别为M、n、n、N。另外，GP算法还需对字典向量进行2M次浮点运算，更新残差M次，更新y系数n次，存储向量长度为M。文献[16]中的OMP-Cholesky算法，则需要额外储存Cholesky分解的n (n+1) /2个元素，以及计算字典和系数的逆迭代，分别为n2、2n2次浮点运算。GP算法与OMP-Cholesky算法的计算复杂度和存储量比较见表 1。
表 1 算法复杂度和存储量Table 1. Algorithms complexity and storage算法 计算复杂度 存储量 OMP-Cholesky 2D+3n2+3M+(D+N) n (n+1) /2+(D+M+2n+N) GP D+n+3M+(D+N) M+(D+M+2n+N) 表 1为2种算法经过一次迭代的计算复杂度和存储量的比较，其中D表示单次迭代的字典计算量或存储量，等价于字典向量乘积运算MN，且有N≥M≥n，可见GP的运算复杂度以及存储量均低于OMP算法。
在KSVD更新中，执行第10) 步的矢量乘法，完成迭代共需要2NK (M+N)次操作，其中N为训练信号的个数，对所有原子的字典更新共需要2MN2次操作，因此，结合第5) 步的稀疏表征计算复杂度，可得到算法的总体计算时间复杂度[17]。
在KSVD算法中，需要存储下标集I，误差矩阵E，字典元素Dj和稀疏矩阵Γ中的各元素g，则存储长度分别为n、MN、MN、N2, 可以得到2种算法的计算机存储量大小：
由上述分析可以看出，GP算法的计算复杂度和储存消耗是最低的。在对测试响应信号的稀疏表征中，由于信号类型多样，可组合形式较多，因此，在对特定信号进行分析时，应选择重构时间最短的方法，本文选择梯度追踪算法进行稀疏表征。但是，稀疏表征中常用的几种固定字典不一定能够很好地反映信号自身的特点，所以考虑将GP稀疏表征进一步结合字典更新的方法——KSVD算法。此外，在KSVD字典训练阶段，已有研究[18]中用OMP结合KSVD算法，而OMP-KSVD算法只适合于处理大规模信号，且通过上述对比可以看出算法的计算复杂度较高，存储量较大，存在局限性。
另一方面在实际应用中，通过运算时间可以直观地反映算法的理论运算复杂度以及计算机存储量状况，下文仿真中分别记录了不同算法的运算时间，并作了比较。
本文为解决电路系统中各类测试响应信号的重构问题，包括小规模信号、大规模信号以及混合信号，将GP算法与KSVD相结合，比较发现GP-KSVD运算复杂度较低，储存消耗少，且对各类信号的重构效果较好，因此，可认为GP-KSVD算法具有普遍适用性。
2. 信号重构原理及评价指标
2.1 信号重构原理
对一维的电路系统测试响应信号进行研究，假设干扰噪声为高斯白噪声，关系式如下：
(2) 式中：x (n)为原始信号；r (n)为高斯白噪声；
对含噪信号的稀疏分解为
(3) 假设r=Dα，则式(3) 可改写为
(4) 对于式(4) 来说，稀疏分解系数Γ是稀疏的，假设非零系数的个数为K，但系数α并不稀疏，且数值较小，因此Γ+α有K个较大系数值。稀疏分解即用K个较大系数对应原子的线性组合来近似表征原始信号，近似表征能够包含绝大部分的有用信号信息，同时滤除大部分的噪声信息，从而实现重构原始信号的目的[8, 23]。
2.2 评价指标
对于信号的重构效果，常用信噪比和相对均方误差2项指标进行评价。具体指标定义如下：
(5) 式中：SNR为信噪比, dB；y (n)为重构信号。
相对均方误差(Relative Mean Square Error, RMSE)为
(6) 信噪比和相对均方误差是信号去噪分析中常用的2项评价指标，在去噪效果的评价中，信噪比越大越好，相对均方误差越小越好[8]。
3. 电路系统常用测试信号重构
3.1 基于训练原子的低频小规模信号重构
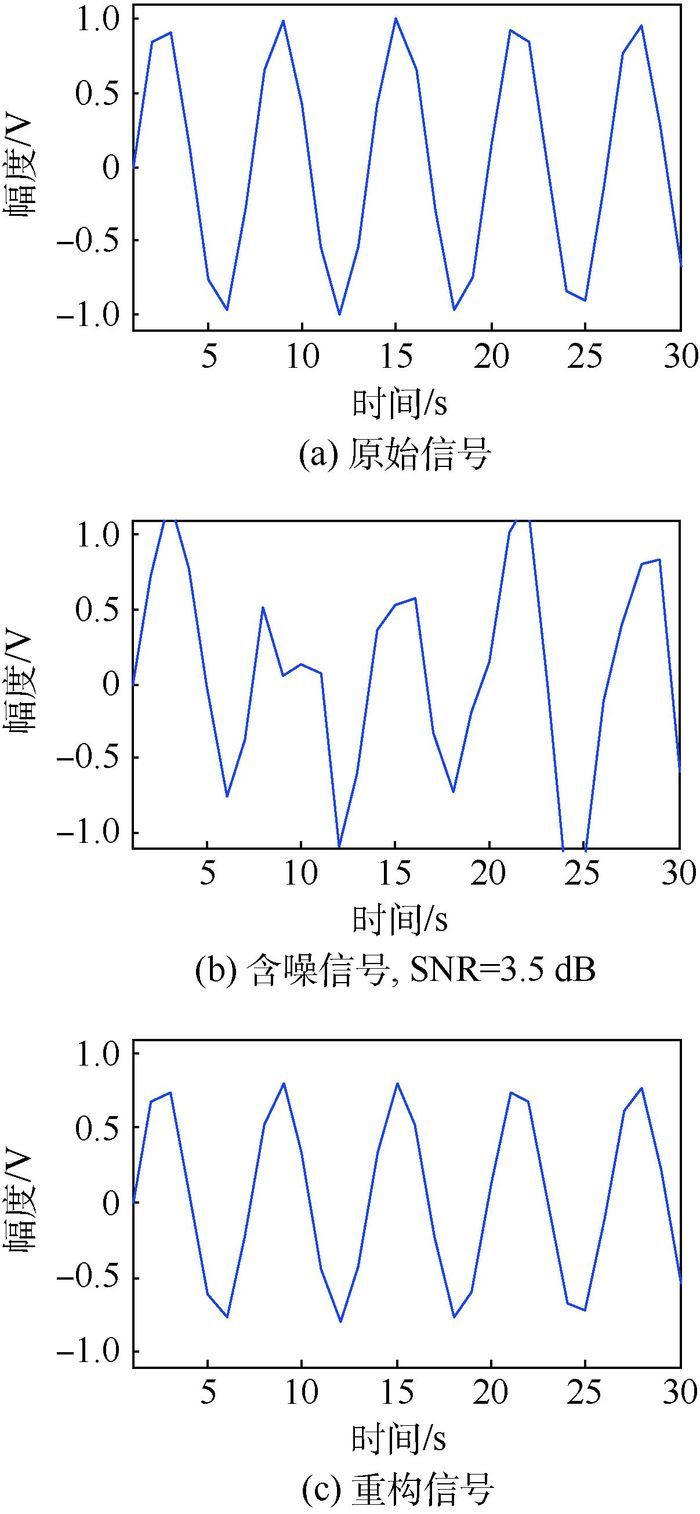
例：测试40组不同频率的正弦信号，频率范围1~40 Hz，将训练数据进行GP-KSVD字典更新，得到匹配字典下的稀疏表示，以f=5 Hz正弦信号为例，根据稀疏系数矩阵确定出表示该信号的字典原子为第25个原子：
添加随机高斯白噪声，含噪信号经过GP稀疏表示后如图 1(b)所示，将原始干净信号的字典原子结合含噪信号的稀疏分布即可实现原始信号的重构，如图 1(c)所示。可见，对于低频且较小规模信号的重构效果是很好的。
3.2 测试信号分段重构
对于大规模信号，采用分段的方式对待处理信号进行字典训练及重构。下例中将包含1 200个数据点的信号分解为40段，每段30个数据点进行处理，以实现更高的匹配程度。
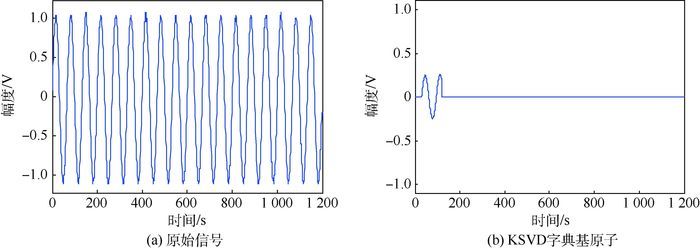
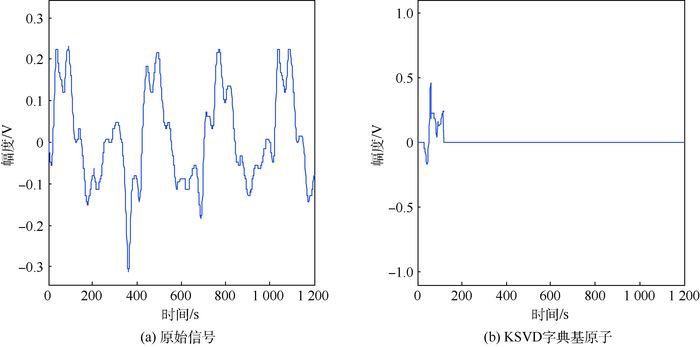
1) 标准正弦信号，频率为1 kHz，采样间隔为2 ns。对分段数据进行训练，得到匹配字典D-KSVD，其中表征信号主要特征的基原子，如图 2所示。
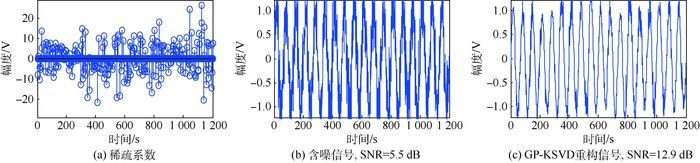
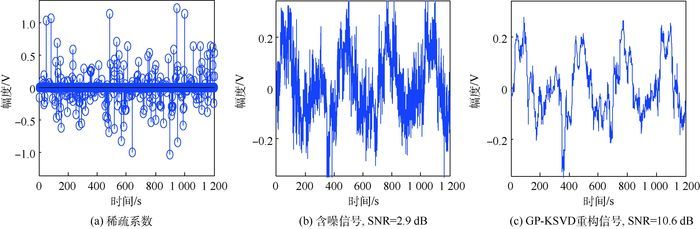
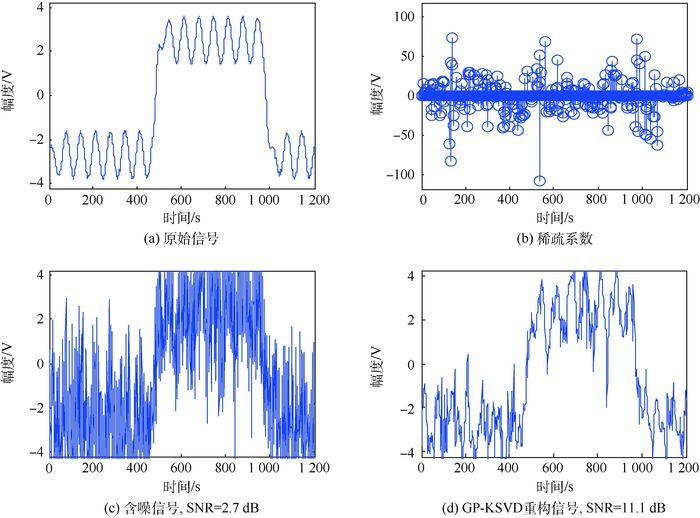
图 2 正弦信号1 kHz以及KSVD字典基原子Figure 2. 1 kHz sine signal and basic atom of KSVD dictionary通过添加高斯白噪声，得到含噪信号，其信噪比SNR=5.5 dB，如图 3所示。用GP算法对含噪信号进行稀疏表征，得到稀疏系数分布如图 3(a)所示，图 3(c)为GP-KSVD重构信号，信噪比提升了7.4 dB。
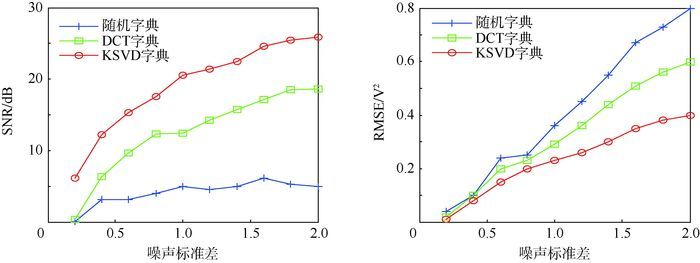
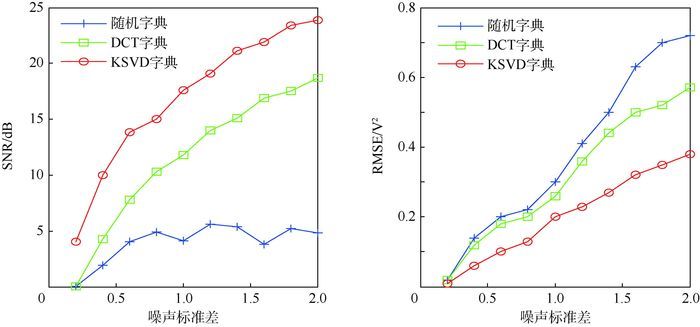
图 3 GP-KSVD对1 kHz正弦信号的重构以及系数表征Figure 3. 1 kHz sine signal reconstruction and coefficient representation by GP-KSVD将本文的GP-KSVD算法与使用随机字典、DCT字典的GP稀疏表征进行对比，3种方法的SNR以及RMSE随噪声标准差的变化情况如图 4所示。
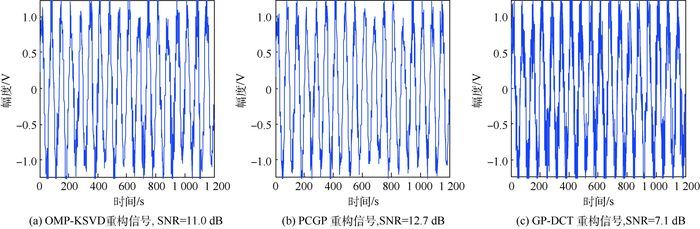
图 4 不同字典处理正弦信号的SNR以及RMSE指标的比较Figure 4. Comparison of index of SNR and RMSE of sine signal processed with different dictionaries将GP-KSVD与预处理共轭梯度追踪(PCGP)算法去噪表征进行比较；同时与GP结合DCT字典、OMP结合KSVD字典方法分别进行比较，结果如图 5所示，对比图 3可以看出GP-KSVD的去噪效果最佳。
图 5 几种不同算法对正弦信号的重构对比Figure 5. Comparison of sine signal reconstruction among different algorithms表 2是几种算法的比较，其中运算时间为对大规模信号分段重构的40次试验的平均时间。可以看出GP-KSVD的运算时间最短，即算法复杂度以及存储量是最低的。
表 2 对正弦信号不同算法的SNR指标以及运行时间Table 2. Index of SNR and running time of different algorithms on sine signal算法 SNR/dB 信噪比增值/dB 运行时间/s PCGP 12.7 7.2 0.162 89 OMP-KSVD 11.0 5.5 0.205 86 GP-DCT 7.1 1.6 0.111 33 GP-KSVD 12.9 7.4 0.097 656 2) 函数型测试信号以f=15 MHz的正切信号为例。
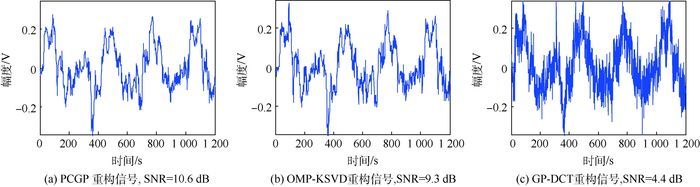
通过表 3及图 6~图 9的比较，对于正切信号而言，利用KSVD字典稀疏去噪，GP跟PCGP的信噪比增幅相同。而选用不同字典时，KSVD字典是几类算法中对信号去噪重构效果最好的，信噪比提升幅度最大，RMSE收敛速度最快。但在运行时间上GP-KSVD仍然是几种算法中最快的。
表 3 对正切信号不同算法的SNR指标以及运行时间Table 3. Index of SNR and running time of different algorithms on tangent signal算法 SNR/dB 信噪比增值/dB 运行时间/s PCGP 10.6 7.7 0.008 984 4 OMP-KSVD 9.3 6.4 0.014 063 GP-DCT 4.4 1.5 0.069 531 GP-KSVD 10.6 7.7 0.005 468 7 
图 6 15 MHz正切信号以及KSVD字典基原子Figure 6. 15 MHz tangent signal and basic atom of KSVD dictionary
图 7 GP-KSVD对15 MHz正切信号的重构以及系数表征Figure 7. 15 MHz tangent signal reconstruction and coefficient representation by GP-KSVD
图 8 不同字典处理正切信号的SNR以及RMSE指标的比较Figure 8. Comparison of indices of SNR and RMSE of tangent signal processed with different dictionaries
图 9 几种不同算法对正切信号的重构对比Figure 9. Comparison of tangent signal reconstruction among different algorithms3) 混合信号分段重构
在混合信号注入测试中，以方波和正弦的混合为例，用1 kHz的方波信号与15 MHz的正弦信号进行混合，得到合成信号，重构情况如图 10所示。
图 10表征了混合信号的GP-KSVD重构过程，可以看到SNR提高8.4 dB，效果明显。
4. 实例对比与实测验证
4.1 实例对比
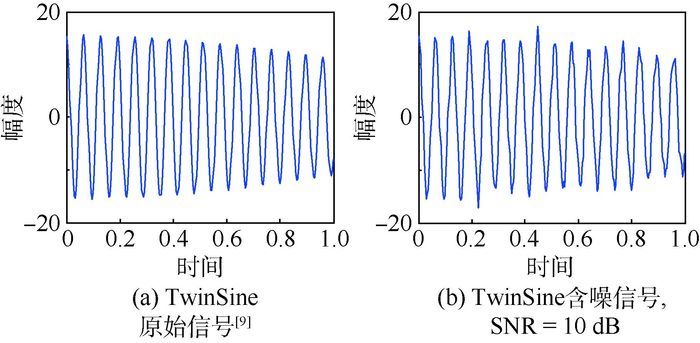
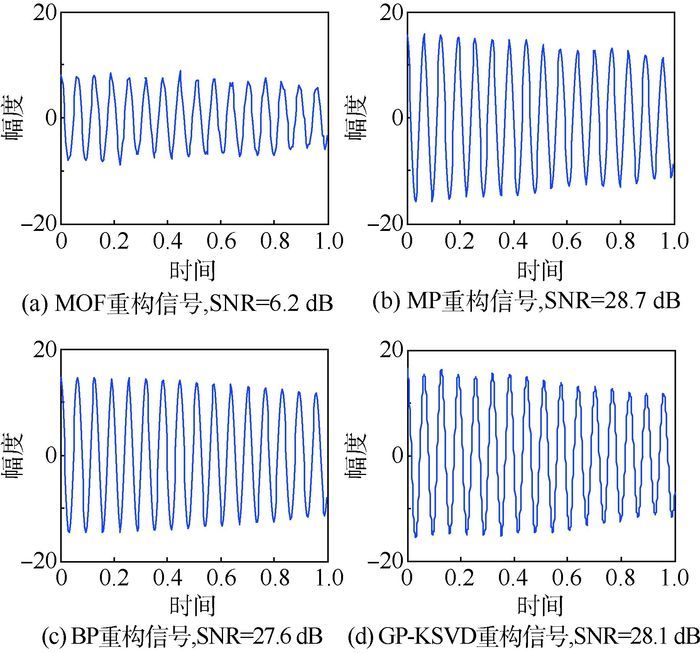
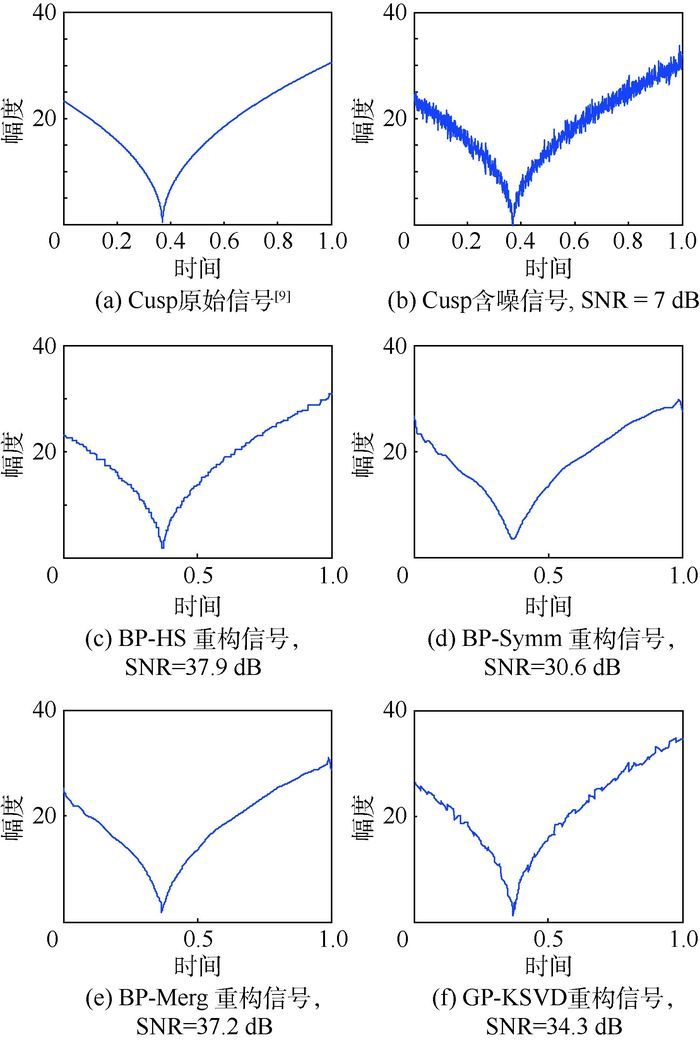
2001年Chen等应用BP、MP、MOF等算法对TwinSine、Cusp、Gong、Blocks等信号进行去噪分析[9]。本节中用GP-KSVD算法对TwinSine以及Cusp信号做去噪处理，与文献[9]的结果进行对比如图 11、图 12、表 4所示。
1) TwinSine信号
通过图 11、图 12以及表 4的分析，将本文的GP-KSVD与文献[9]中用MOF、MP、BP 3种算法对TwinSine信号的去噪结果进行比较，发现在SNR指标上相差较小，但GP-KSVD算法在计算机运行时间上是最短的。
2) Cusp信号
由图 13以及表 5的分析可以看出，在指标SNR差异不明显的情况下，GP-KSVD算法的计算机运行时间仍是最短的。
本节通过GP-KSVD与文献[9]中提出的2种信号的去噪结果进行对比，证明了本文算法计算速度快，用时短的特点，优势明显。
4.2 实测验证
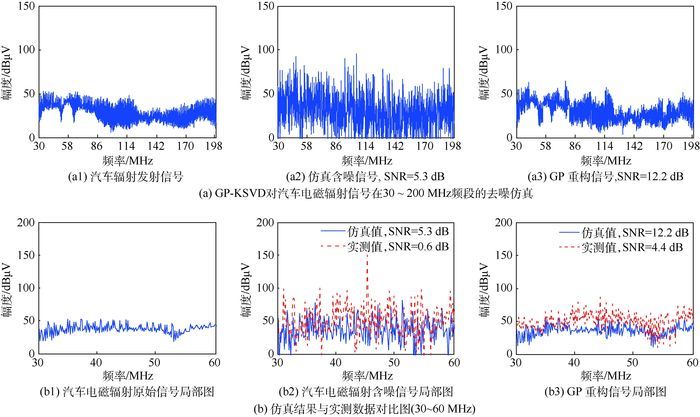
为更好地验证本文算法的有效性以及普遍适用性，针对民用汽车的电磁辐射信号进行了实验测试以及数据提取分析。实验选在标准10 mF电磁兼容实验室，被试物品为民用中巴汽车，载量为15人，被试品状态为打火状态，测量辐射频段为30~200 MHz，选用匹配的喇叭天线进行测试，数据分析结果以及实验现场测试图如图 14和图 15所示。
图 14 GP-KSVD对电磁辐射信号的去噪重构Figure 14. Denoising reconstruction of electromagnetic radiation signal by GP-KSVD图 14(a)为30~200 MHz全频段的仿真处理前后对比图，图 14(b)为仿真数据和实测数据的对比结果，由于数据点过密，为方便对比，图中为局部放大频段30~60 MHz。其中，对于仿真信号的处理，信噪比提升6.9 dB；对实测信号的处理，信噪比提升3.8 dB，误差在3 dB左右。这是由于仿真中添加的是高斯白噪声，而实测环境数据则包含了工业噪声、交通噪声、生活噪声等，因此去噪重构结果存在一定的差异。然而，在实际电路系统中，例如雷达、通信系统的噪声来源主要是热噪声，即典型的高斯白噪声，因此本文算法选用高斯白噪声进行仿真还是比较具有实际意义的。
汽车在30~200 MHz频段最易受扰，因此针对该频段的电磁辐射发射进行实验，从图 14中可以看到，运用GP-KSVD算法对仿真和实测信号的处理效果都较明显，证明了算法的有效性。
5. 结论
1) 本文提出的GP-KSVD算法实现了对单一的小规模正弦信号进行直接重构，对大规模正弦测试信号、正切函数测试信号以及方波与正弦的混合信号进行分段重构。
2) 通过SNR、RMSE 2个指标将GP-KSVD分别与GP结合随机字典、GP-DCT稀疏表征进行比较，得到GP-KSVD的信噪比最优、去噪效果最好、相对均方根误差最小的结论。
3) 将GP-KSVD分别与OMP-KSVD、PCGP算法进行重构比较，得到GP-KSVD重构信号的信噪比最高，运算时间最短，重构效果最好的结论。
分析结果表明，GP-KSVD算法可用于电路系统设备测试响应信号预处理中，为电路系统设备性能评估提供了前提和基础。然而，本方算法仍然存在需要大量训练数据以及先验知识做基础的局限性，算法的应用性有待讨论，在今后的工作中将做进一步改进。
致谢: 致谢感谢实验室老师的指导以及许立登同学、尚晓凡同学的无私帮助。 -
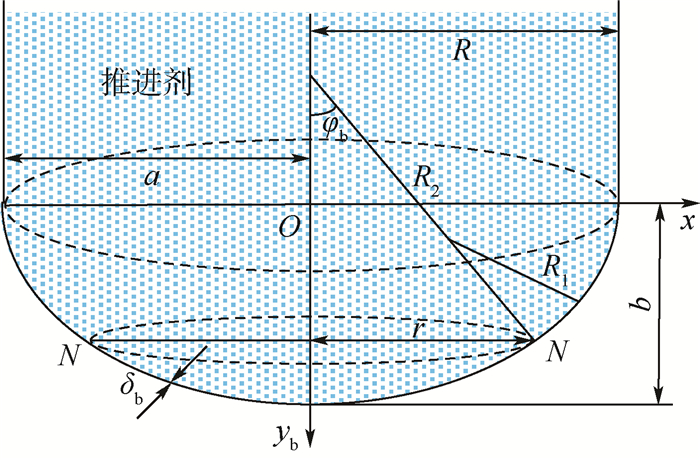
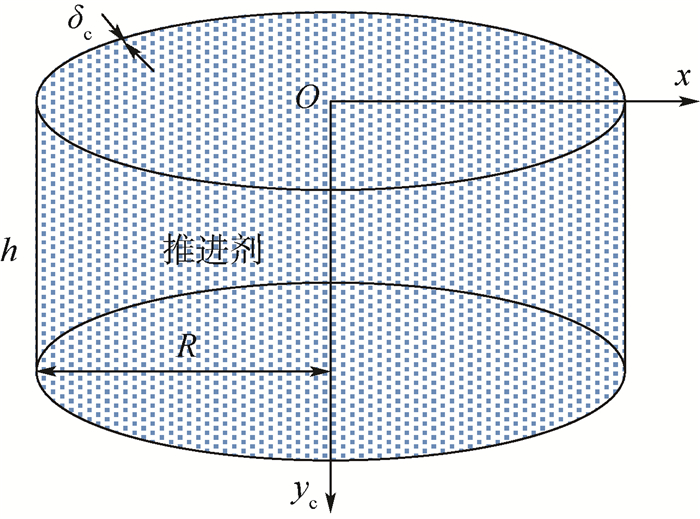
表 1 贮箱及推进剂参数
Table 1. Parameters of tank and propellant
参数 m a/mm h/mm ρ/(kg·m-3) ΔP/Pa 数值 1.6 1 669 8 080 1 458 101 325 
下载: 导出CSV
表 2 下底、上底壁厚参数
Table 2. Thickness parameters of bottom and roof
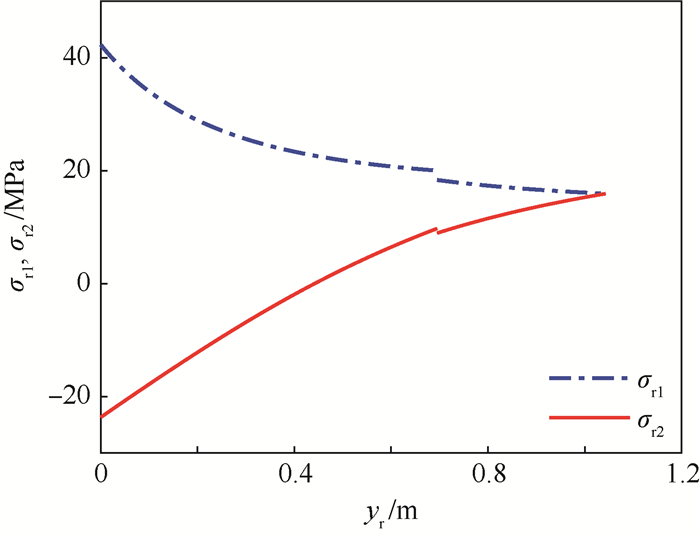
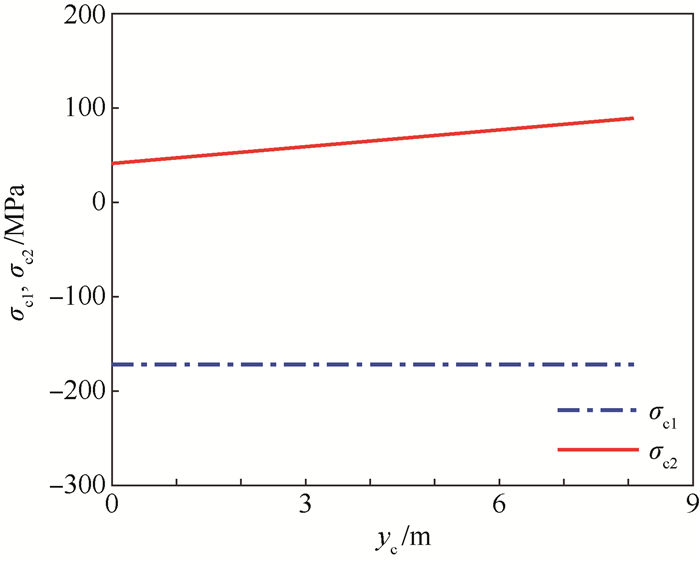
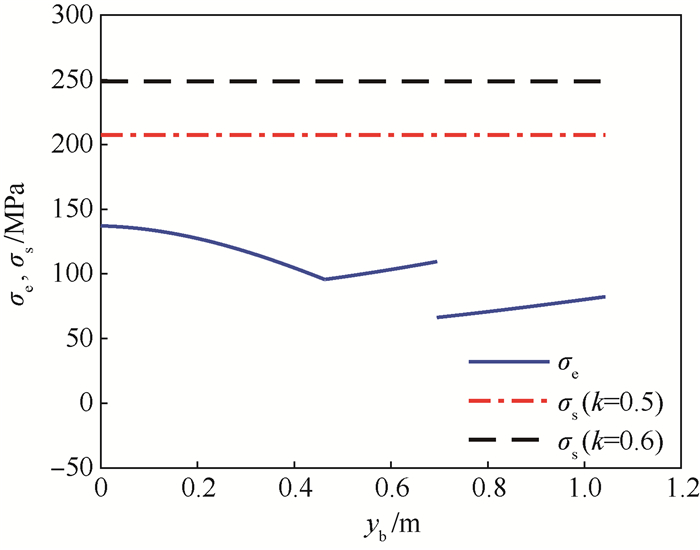
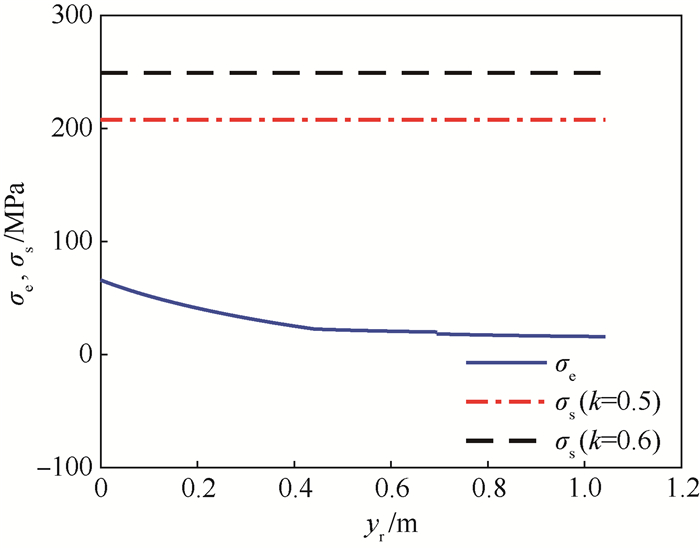
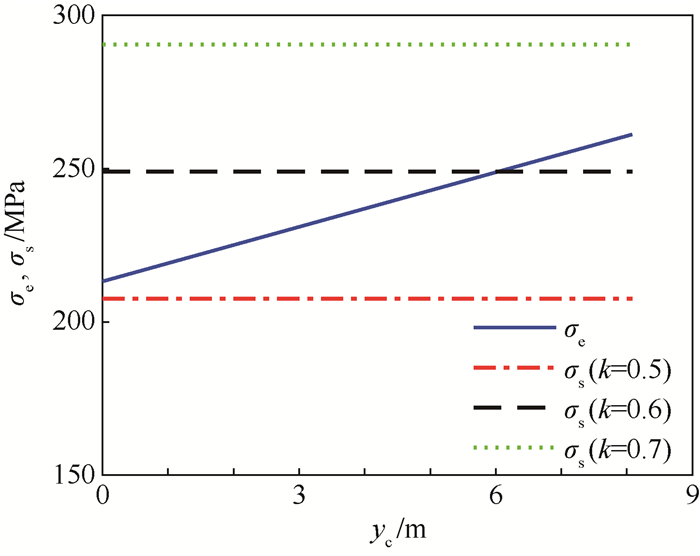
区间/mm δb/mm δr/mm 0≤yb(yr) < 695 2.3 2.0~5.5 695≤yb(yr)≤b 3.8 6.0~8.5
下载: 导出CSV
表 3 等效应力区间凸集
Table 3. Interval convex set of equivalent stress
MPa 结构 Smin Smax 下底 66.27 137.13 上底 15.91 65.96 圆柱筒 213.25 261.20
下载: 导出CSV
表 4 贮箱应力强度可靠性指标
Table 4. Stress strength reliability index of tank
结构 指标 k=0.7, 0.8 k=0.6, 0.7 k=0.5, 0.6 下底 η 3.73 2.99 2.25 ηe 5.10 4.09 3.08 上底 η 5.91 5.00 4.09 ηe 8.32 7.04 5.76 圆柱筒 η 1.66 0.96 0.32 ηe 2.33 1.03 -0.28
下载: 导出CSV
-
[1] 王心清.结构设计[M].2版.北京:中国宇航出版社, 2009:19-35.WANG X Q.The structural design[M].2nd ed.Beijing:China Astronautic Publishing House, 2009:19-35(in Chinese). [2] 张俊苗.航天器贮箱铝合金焊接接头强度特性研究[D].南京: 南京航空航天大学, 2013: 1-14ZHANG J M.Investigation on strength properties of alumini-um alloy weld joint in spacecraft tank[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2013: 1-14(in Chinese). [3] NACHTIGALL I, GEBBEKEN N, URRUTIA-GALICIA J L.On the analysis of vertical circular cylindrical tanks under earthquake excitation at its base[J].Engineering Structures, 2003, 25(2):201-213. doi: 10.1016/S0141-0296(02)00135-9 [4] JHA A K, NARAYANAN P R, SREEKUMAR K, et al.Cracking of Al-4.5Zn-1.5Mg aluminium alloy propellant tank-A metallurgical investigation[J].Engineering Failure Analysis, 2010, 17:562-570. doi: 10.1016/j.engfailanal.2009.10.009 [5] JHA A K, MURTY S V S N, SREEKUMAR K, et al.High strain rate deformation and cracking of AA 2219 aluminium alloy we-lded propellant tank[J].Engineering Failure Analysis, 2009, 16(7):2209-2216. doi: 10.1016/j.engfailanal.2009.03.001 [6] BEN-HAIM Y.Convex models of uncertainty in applied mecha-nics[M].New York:Elsevier Science Publishers, 1990:151-157. [7] BEN-HAIM Y.A non-probabilistic concept of reliability[J].Structural Safety, 1994, 14(4):227-245. doi: 10.1016/0167-4730(94)90013-2 [8] ELISHAKOFF I, BEN-HAIM Y.Dynamics of a thin cylindrical shell under impact with limited deterministic information on its initial imperfections[J].Structural Safety, 1990, 8(1):103-112. [9] 邱志平, 胡永明.椭球凸模型非概率可靠性度量和区间安全系数的关系[J].计算力学学报, 2016, 33(4):522-527.QIU Z P, HU Y M.The relations of non-probabilistic reliabilitymeasures based on ellipsoidal convex model and interval safety factors[J].Chinese Journal of Computational Mechanics, 2016, 33(4):522-527(in Chinese). [10] 王晓军.不确定初始几何缺陷杆动态屈曲失效分析[J].北京航空航天大学学报, 2011, 37(12):1484-1489.WANG X J.Dynamic buckling failure analysis of rod with uncertain initial geometrical imperfection[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12):1484-1489(in Chinese). [11] WANG R X, WANG X J, WANG L, et al.Efficient computational method for the non-probabilistic reliability of linear structural systems[J].Acta Mechanica Solida Sinica, 2016, 29(3):284-301. doi: 10.1016/S0894-9166(16)30162-8 [12] JIANG C, BI R G, LU G Y, et al.Structural reliability analysis using non-probabilistic convex model[J].Computer Methods in Applied Mechanics and Engineering, 2013, 254:83-98. doi: 10.1016/j.cma.2012.10.020 [13] GUO S X, LU Z Z.A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters[J].Applied Mathematical Modelling, 2014, 26:3-15. [14] COURTOIS C, DENUIT M.Bounds on convex reliability functions with known first moments[J].Stochastics and Statistics, 2007, 177(1):365-377. [15] KARUNA K, MANOHAR C S.Inverse problems in structural safety analysis with combined probabilistic and non-probabilistic uncertainty models[J].Engineering Structures, 2017, 150:166-175. doi: 10.1016/j.engstruct.2017.07.044 [16] 赵亮.大直径薄壁箱体结构力学分析与精细优化设计[D].大连: 大连理工大学, 2015: 32-36.ZHAO L.The mechanical analysis and refined optimization of large-diameter and thin-walled tank structures[D].Dalian: Dalian University of Technology, 2015: 32-36(in Chinese). [17] 刘雨均.运载火箭总体与结构[M].北京:国防工业出版社, 2003:206-217.LIU Y J.Launch vehicle overall and structure[M].Beijing:National Defence of Industry Press, 2003:206-217(in Chinese). [18] 张娜.非概率可靠度理论相关问题研究[D].柳州: 广西科技大学, 2015: 17-22.ZHANG N.The research of non-probability reliability[D].Liuzhou: Guangxi University of Science and Technology, 2015: 17-22(in Chinese). 期刊类型引用(2)
1. 姜峰，李华聪，符江锋，洪林雄. 基于RBF和主动学习的非概率可靠度求解方法. 航空学报. 2023(02): 213-227 . 
百度学术2. 齐金平，周亚辉，王康，李少雄. 受电弓系统可靠性评估的超椭球贝叶斯网络方法. 兰州理工大学学报. 2022(04): 105-110 . 百度学术其他类型引用(1)
-
下载:
下载:
百度学术
点击查看大图
计量
- 文章访问数: 845
- HTML全文浏览量: 158
- PDF下载量: 298
- 被引次数: 3
