A new moment-independent importance measure analysis method and its efficient algorithm
-
摘要:
为了更加合理地分析输入随机变量对结构系统失效概率的影响，提出了一种新的矩独立重要性测度分析方法。传统的重要性测度指标只能估计输入随机变量在固定点时对结构系统输出响应的影响，而所提新指标能够充分反映输入随机变量在其分布区域的所有缩减区间上变化时对结构系统输出响应的平均影响程度，更加符合工程实际。为了求解新指标，给出了2种算法：传统的双层重复抽样蒙特卡罗（DLRS MC）方法和自适应超球重要抽样（ARBIS）方法。双层重复抽样蒙特卡罗方法计算结果可以作为对比参照解，但求解效率较低，计算量很大；自适应超球重要抽样方法在满足新指标求解精度的前提下，计算效率得到很大提高。应用数值算例和工程算例证明了所提新指标的意义和所提新算法的高效性。
Abstract:In order to analyze the effect of input random variables on the failure probability of structural systems more reasonably, a new moment-independent importance measure analysis method is proposed in this paper. The traditional importance measure index can only estimate the influence of input random variables on the output response of structural systems at fixed points, while the new index proposed in this paper can fully reflect the average influence of input random variables on the output response of structural systems when they change in all reduced intervals of their distribution areas, which is more in line with engineering practice. Seeking to find the new index, this paper presents two algorithms:the conventional double-loop-repeated-set Monte Carlo (DLRS MC) method and adaptive radial-based importance sampling (ARBIS) method. The results of DLRS MC method can be used as a reference solution, yet its calculation process is slow and strenuous. Under the condition of the precision of solving the new index is met, the calculation efficiency of ARBIS method is greatly improved. Finally, a numerical example and an engineering example are given to illustrate the significance of the new index and the efficiency of the proposed algorithm.
-
图 2 DLRS MC方法和ARBIS方法计算的新的矩独立重要性测度指标的收敛曲线
Figure 2. Convergence curves of new moment-independent importance measure indices of numerical example computed by DLRS MC and ARBIS methods
图 4 DLRS MC方法和ARBIS方法计算汽车前轴的收敛曲线
Figure 4. Convergence curves of automobile front axle computed by DLRS MC and ARBIS methods
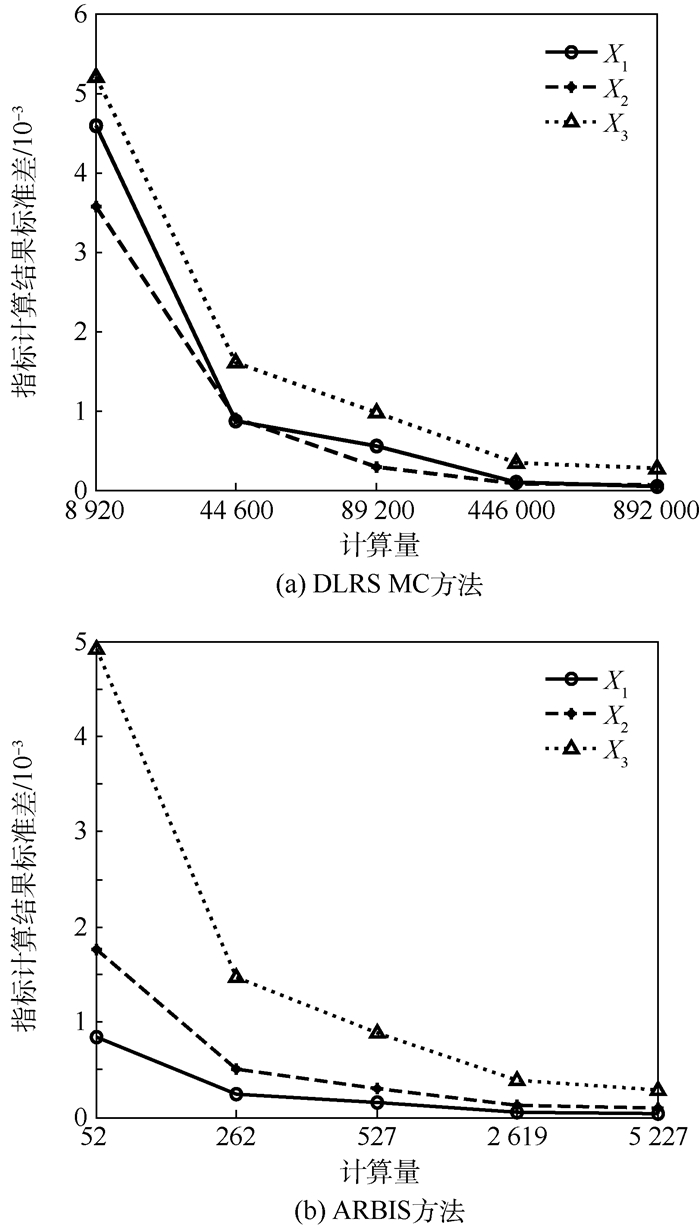
表 1 DLRS MC方法和ARBIS方法计算的新的矩独立重要性测度指标值
Table 1. New moment-independent importance measure indices of numerical example computed by DLRS MC and ARBIS methods
随机变量 DLRS MC方法 ARBIS方法 δiP/10-2 SD/10-2 δiP/10-2 SD/10-2 X1 0.061 0 0.010 0.058 2 0.048 X2 0.226 4 0.007 0.216 7 0.013 X3 1.257 2 0.035 1.217 4 0.039 计算量 446 000 2 619 
下载: 导出CSV
表 2 汽车前轴结构各输入变量分布参数
Table 2. Distribution parameters of input variables of automobile front axle structure
随机变量 均值 标准差 a/mm 12 0.60 b/mm 65 3.25 t/mm 14 0.70 h/mm 85 4.25 M/(N·mm) 3.5×106 7.5×105 T/(N·mm) 3.1×106 1.5×105
下载: 导出CSV
表 3 DLRS MC方法和ARBIS方法计算汽车前轴指标结果
Table 3. Results of indices of automobile front axle computed by DLRS MC and ARBIS methods
随机变量 DLRS MC方法 ARBIS方法 δiP SD/10-3 δiP SD/10-3 a 0.004 9 0.276 0.004 7 0.249 b 0.006 4 0.394 0.006 2 0.333 t 0.016 3 0.546 0.015 7 0.608 h 0.001 4 0.173 0.001 3 0.149 M 6.49×10-5 0.092 1.95×10-5 0.012 T 0.009 5 0.426 0.009 2 0.321 计算量 446 000 4 475
下载: 导出CSV
-
[1] CASTILLO E, MINGUEZ R, CASTILLO C.Sensitivity analysis in optimization and reliability problems[J].Reliability Engineering & System Safety, 2008, 93(12):1788-1800. http://www.sciencedirect.com/science/article/pii/S0951832008000999 [2] WEI P, LV Z, HAO W, et al.Efficient sampling methods for global reliability sensitivity analysis[J].Computer Physics Communications, 2012, 183(8):1728-1743. doi: 10.1016/j.cpc.2012.03.014 [3] SALTELLI A.Sensitivity analysis for importance assessment[J].Risk Analysis, 2002, 22(3):579-590. http://d.old.wanfangdata.com.cn/Periodical/jsjyxdh201804013 [4] BJERAGER P, KRENK S.Parametric sensitivity in first order reliability theory[J].Journal of Engineering Mechanics, 1989, 115(7):1577-1582. doi: 10.1061/(ASCE)0733-9399(1989)115:7(1577) [5] CAMPOLONGO F, SALTELLI A.Sensitivity analysis of an environmental model:An application of different analysis methods[J].Reliability Engineering & System Safety, 1997, 57(1):49-69. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_348a65a521d0dda5145fd990380d0dcc [6] SALTELLI A, RATTO M, TARANTOLA S, et al.Sensitivity analysis for chemical models[J].Chemical Reviews, 2005, 105(7):2811-2828. doi: 10.1021/cr040659d [7] BORGONOVO E, TARANTOLA S.Moment independent and variance-based sensitivity analysis with correlations:An application to the stability of a chemical reactor[J].International Journal of Chemical Kinetics, 2008, 40(11):687-698. doi: 10.1002/kin.v40:11 [8] VAN GRIENSVEN A, MEIXNER T, GRUNWALD S, et al.A global sensitivity analysis tool for the parameters of multi-variable catchment models[J].Journal of Hydrology, 2006, 324(1):10-23. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dcff851294130479e8e4dca6364de521 [9] SALTELLI A, MARIVOET J.Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J].Reliability Engineering & System Safety, 1990, 28(2):229-253. http://www.sciencedirect.com/science/article/pii/095183209090065U [10] HELTON J C.Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal[J].Reliability Engineering & System Safety, 1993, 42(2):327-367. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=21e1efbd47a61dbb4e5384e17c5572f0 [11] SOBOL I M.Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics and Computers in Simulation, 2001, 55(1):271-280. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=84bf6510004c1dd0e68e68e1ce4e738f [12] IMAN R L, HORA S C.A robust measure of uncertainty importance for use in fault tree system analysis[J].Risk Analysis, 1990, 10(3):401-406. doi: 10.1111/j.1539-6924.1990.tb00523.x/full [13] HELTON J C, DAVIS F J.Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J].Reliability Engineering & System Safety, 2003, 81(1):23-69. http://www.sciencedirect.com/science/article/pii/S0951832003000589 [14] BORGONOVO E.A new uncertainty importance measure[J].Reliability Engineering & System Safety, 2007, 92(6):771-784. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0911.1455 [15] LIU H, CHEN W, SUDJIANTO A.Relative entropy based method for probabilistic sensitivity analysis in engineering design[J].Journal of Mechanical Design, 2006, 128(2):326-336. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0212203414/ [16] LI L Y, LU Z Z, FENG J, et al.Moment-independent importance measure of basic variable and its state dependent parameter solution[J].Structural Safety, 2012, 38:40-47. doi: 10.1016/j.strusafe.2012.04.001 [17] WEI P, LU Z, SONG J.A new variance-based global sensitivity analysis technique[J].Computer Physics Communications, 2013, 184(11):2540-2551. doi: 10.1016/j.cpc.2013.07.006 [18] GROOTEMAN F.Adaptive radial-based importance sampling method for structural reliability[J].Structural Safety, 2008, 30(6):533-542. doi: 10.1016/j.strusafe.2007.10.002 [19] AU S K, BECK J L.A new adaptive importance sampling scheme for reliability calculations[J].Structural Safety, 1999, 21(2):135-158. doi: 10.1016/S0167-4730(99)00014-4 [20] ROSENBLATT M.Remarks on a multivariate transformation[J].The Annals of Mathematical Statistics, 1952, 23(3):470-472. doi: 10.1214-aoms-1177729394/ [21] DER KIUREGHIAN A, LIU P L.Structural reliability under incomplete probability information[J].Journal of Engineering Mechanics, 1986, 112(1):85-104. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0229412452/ [22] 吕震宙.结构机构可靠性及可靠性灵敏度分析[M].北京:科学出版社, 2009:160-178.LV Z Z.Reliability and reliability sensitivity analysis of structural mechanism[M].Beijing:Science Press, 2009:160-178(in Chinese). [23] CAI Z Y.Precision design of roll-forging die and its application in the forming of automobile front axles[J].Journal of Materials Processing Technology, 2005, 168(1):95-101. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=5aaddc0b35e2381e8ca86cefa9d91c4e -
下载:
点击查看大图
计量
- 文章访问数: 567
- HTML全文浏览量: 20
- PDF下载量: 361
- 被引次数: 0
