模糊-随机混合参数的机构运动可靠度计算方法

游令非; 张建国; 翟浩; 李桥

doi:10.13700/j.bh.1001-5965.2018.0433

模糊-随机混合参数的机构运动可靠度计算方法

doi: 10.13700/j.bh.1001-5965.2018.0433

游令非^{1, 2},
张建国^{1, 2, ,},
翟浩^{1, 2},
李桥^{1, 2}

1.
北京航空航天大学可靠性与系统工程学院, 北京 100083
2.
北京航空航天大学可靠性与环境工程技术国防科技重点实验室, 北京 100083

基金项目:

国家自然科学基金 51675026

详细信息

作者简介:
游令非男, 博士研究生。主要研究方向:结构/机构可靠性

张建国男, 博士, 教授, 博士生导师。主要研究方向:机械/结构/机构可靠性

通讯作者:
张建国, E-mail: zjg@buaa.edu.cn

中图分类号: V415.4;TB114.3
计量
- 文章访问数: 656
- HTML全文浏览量: 71
- PDF下载量: 329
- 被引次数: 0
出版历程
- 收稿日期: 2018-07-17
- 录用日期: 2018-10-15
- 网络出版日期: 2019-04-20

Computation method on motional reliability of mechanism under mixed parameters with fuzziness and randomness

YOU Lingfei^{1, 2},
ZHANG Jianguo^{1, 2
, ,},
ZHAI Hao^{1, 2},
LI Qiao^{1, 2}

1.
School of Reliability and System Engineering, Beihang University, Beijing 100083, China
2.
Science and Technology on Reliability and Environmental Engineering Laboratory, Beihang University, Beijing 100083, China

Funds:

National Natural Science Foundation of China 51675026

More Information

Corresponding author: ZHANG Jianguo, E-mail: zjg@buaa.edu.cn

摘要

摘要:
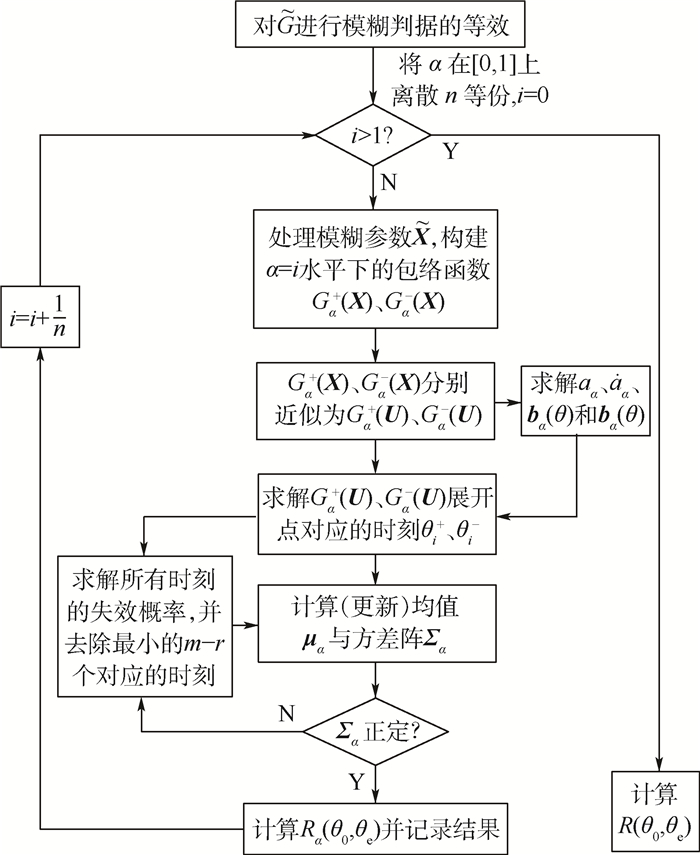
在目前机构产品的参数当中普遍存在着模糊变量和随机变量混合的情况，而现有的模糊-随机可靠度求解方法一般针对静态问题进行分析，不能有效描述具有混合不确定性的机构运动时变问题。基于机构运动误差分析，同时考虑失效判据和变量的模糊性，提出了基于改进包络函数的模糊-随机时变机构可靠性建模及计算方法。首先，将模糊判据转化为极限状态方程中的随机变量；其次，利用模糊论中的截集法处理模糊-随机混合变量，建立机构产品的模糊-随机时变可靠性模型；再次，利用改进的包络函数计算机构的运动时变可靠度；最后，结合四连杆机构的运动误差问题，验证了本文方法的可行性，结果表明该方法具有较高的计算精度。
- 包络函数 /
- 模糊 /
- 时变可靠度 /
- 运动误差 /
- 截集
Abstract:
Mixed uncertainties of random variables and fuzzy variables are ubiquitous in the parameters of the current mechanism products, but the existing fuzzy reliability model mainly aims at static problems, which cannot describe the time-dependent problem with mixed uncertainty. This paper proposes a reliability modeling and computation method of the fuzzy time-dependent mechanism based on the advanced envelope function through the kinematic error analysis of mechanism and considering the fuzziness of failure criterion and the variables. First, fuzzy criterion can be transferred into random variables in the limit state function. Then, the cut set of fuzzy theory can be used to deal with the fuzzy and random variables, and thus the fuzzy time-dependent reliability model is built. After that, the advanced envolope function is used to calculate the time-dependent reliability of the mechanism. Finally, the feasibility of the method is verified by the motion error issue of four-bar linkage. The results show that the method has high computational accuracy.
- envelope function /
- fuzzy /
- time-dependent reliability /
- motion error /
- cut set

HTML全文

图 1 机构运动误差的包络函数

Figure 1. Envelope functions of mechanism motion error

下载: 全尺寸图片幻灯片

图 2 运动误差的失效隶属度函数

Figure 2. Membership function of motion error failure

下载: 全尺寸图片幻灯片

图 3 阈值模糊的时变可靠性失效事件描述

Figure 3. Failure event description of time-dependent reliability based on fuzzy threshold

下载: 全尺寸图片幻灯片

图 4 基于改进包络函数的可靠度计算方法流程

Figure 4. Flowchart of reliability computation method based on advanced envelope function

下载: 全尺寸图片幻灯片

图 5 四连杆机构

Figure 5. Four-bar linkage mechanism

下载: 全尺寸图片幻灯片

图 6 变量取均值时的运动误差变化

Figure 6. Motion error change at means of variables

下载: 全尺寸图片幻灯片

图 7 ε=0.5时可靠度随截集水平α的变化

Figure 7. Change of reliability with cut set level α when ε=0.5

下载: 全尺寸图片幻灯片

图 8 0°~90°的失效概率

Figure 8. Probability of failure at 0°-90°

下载: 全尺寸图片幻灯片

表 1 α水平下尺寸随机变量的数字特征

Table 1. Numerical characteristics of random dimension variables under α level

变量均值标准差分布类型

R₁ 10 0.1 正态分布

(R₂)_α 50 3(α－1)²/20000 正态分布

R₃ 40 0.1 正态分布

R₄ 40 0.1 正态分布

下载: 导出CSV

表 2 时变可靠度计算结果

Table 2. Computation results of time-dependent reliability

ε/(°) 本文方法 MCS法

0.70 0.714 25 0.713 83

0.80 0.836 45 0.836 11

0.90 0.914 07 0.913 67

1.00 0.958 25 0.957 94

1.10 0.981 31 0.981 03

1.20 0.992 32 0.992 18

下载: 导出CSV

参考文献(17)

[1]	拓耀飞, 陈建军, 陈永琴.区间参数弹性连杆机构的非概率可靠性分析[J].中国机械工程, 2007, 18(5):528-563. doi: 10.3321/j.issn:1004-132X.2007.05.007 TUO Y F, CHEN J J, CHEN Y Q.Non-probabilistic reliability analysis of elastic linkage mechanism with interval parameters[J].China Mechanical Engineering, 2007, 18(5):528-563(in Chinese). doi: 10.3321/j.issn:1004-132X.2007.05.007
[2]	TUO Y F, CHEN J J, ZHANG C J, et al.Reliability analysis of kinematic acuuracy for the elastic slider-crank mechanism[J].Frontiers of Mechanical Engineering in China, 2007, 2(2):214-217. doi: 10.1007/s11465-007-0037-3
[3]	董玉革, 陈心昭, 赵显德, 等.模糊可靠性理论在机构运动可靠性分析中的应用[J].应用科学学报, 2002, 20(3):316-320. http://d.old.wanfangdata.com.cn/Periodical/yykxxb200203022 DONG Y G, CHEN X Z, ZHAO X D, et al.An application of fuzzy reliability theory in the reliability analysis of mechanism movement[J].Journal of Applied Sciences, 2002, 20(3):214-217(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/yykxxb200203022
[4]	张义民, 黄贤振, 贺向东, 等.不完全概率信息牛头刨床机构运动精度可靠性稳健设计[J].机械工程学报, 2009, 45(4):105-109. http://d.old.wanfangdata.com.cn/Periodical/jxgcxb200904018 ZHANG Y M, HUANG X Z, HE X D, et al.Reliability-based robust design for kinematic accuracy of the shaper mechanism under incomplete probability information[J].Journal of Mechanical Engineering, 2009, 45(4):105-109(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jxgcxb200904018
[5]	张义民, 黄贤振, 贺向东.任意分布参数平面连杆机构运动精度可靠性稳健设计[J].农业机械学报, 2008, 39(7):139-143. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb200807031 ZHANG Y M, HUANG X Z, HE X D.Reliability-based robust design for kinematic accuracy of the planar linkage mechanism with arbitrary distribution parameters[J]Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(7):139-143(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/nyjxxb200807031
[6]	ZHANG J F, DU X P.Time-dependent reliability analysis for function generator mechanisms[J].Journal of Mechanical Design, 2011, 133(3):031005. doi: 10.1115/1.4003539
[7]	ANDERIEU-RENAUD C, SUDERT B, LEMAIRE M, et al.The PHI2 method:A way to compute time-variant reliability[J].Reliability Engineering and System Safety, 2004, 84(1):74-86. http://cn.bing.com/academic/profile?id=ceb8340f023967a754505877b27d6564&encoded=0&v=paper_preview&mkt=zh-cn
[8]	MEJRI M, CAZUGEL M, COGNARD J Y, et al.A time-variant reliability approach for aging marine structures with nonlinear behavior[J].Computers & Structures, 2011, 89(19-20):1742-1753. https://www.researchgate.net/publication/47723851_A_time-variant_reliability_approach_for_ageing_marine_structures_with_non_linear_behavior
[9]	LI J, CHEN J B, FAN W L.The equivalent extreme-value event and evaluation of the structural system reliability[J].Structure Safety, 2007, 29(2):112-131. doi: 10.1016/j.strusafe.2006.03.002
[10]	马小兵, 任宏道, 蔡义坤.高温结构可靠性分析的时变响应面法[J].北京航空航天大学学报, 2015, 41(2):198-202. http://bhxb.buaa.edu.cn/CN/abstract/abstract13148.shtml MA X B, REN H D, CAI Y K.Time-varying response surface method for high-temperature structural reliability analysis[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2):198-202(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13148.shtml
[11]	DU X P.Time-dependent mechanism reliability analysis with envelope function and first-order approximation[J].Journal of Mechanical Design, 2014, 136(8):081010. doi: 10.1115/1.4027636
[12]	ZHANG J F, DU X P.Time-dependent reliability analysis for function generation mechanisms with random joint clearances[J].Mechanism and Machine Theory, 2015, 92:184-199. doi: 10.1016/j.mechmachtheory.2015.04.020
[13]	WEI P F, SONG J W, LU Z Z, et al.Time-dependent reliability sensitivity analysis of motion mechanisms[J].Reliability Engineering and System Safety, 2016, 149:107-120. doi: 10.1016/j.ress.2015.12.019
[14]	WEI P F, WANG Y Y, TANG C H.Time-variant global reliability sensitivity analysis of structures with both input random variables and stochastic processes[J].Structural and Multidisciplinary Optimization, 2017, 55(5):1883-1898. doi: 10.1007/s00158-016-1598-8
[15]	张明.结构可靠度分析-方法与程序[M].北京.科学出版社, 2009:204-206. ZHANG M.Structural reliability analysis:Method and prosedures[M].Beijing:Science Press, 2009:204-206(in Chinese).
[16]	WANG Z L, HUANG H Z, LI Y F, et al.An approach to system reliability analysis wiyh fuzzy random variables[J].Mechanism and Machine Theory, 2012, 52:35-46. doi: 10.1016/j.mechmachtheory.2012.01.007
[17]	张萌, 陆山.模糊可靠性模型的收敛性及改进的截集分布[J].北京航空航天大学学报, 2014, 40(8):1109-1115. http://bhxb.buaa.edu.cn/CN/abstract/abstract13004.shtml ZHANG M, LU S.Convergence of fuzzy reliability models and an improved cut-set distribution[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(8):1109-1115(in Chinese). http://bhxb.buaa.edu.cn/CN/abstract/abstract13004.shtml