-
摘要:
微惯性测量单元（MIMU）的标定技术是低精度惯性导航领域中的重要研究方向，传统标定方法操作复杂，标定精度严重依赖转台精度。为解决大批量MIMU快速标定的问题，提出了一种基于自适应遗传算法（GA）的微机电系统（MEMS）加速度计快速标定方法，将加速度计标定问题转化为参数优化问题。首先，利用模观测原理构造目标优化函数；然后，分析系统可观测度确定最优标定编排方案；最后，采用全局搜索的自适应遗传算法优化标定参数。实验结果表明：与牛顿迭代法相比，标定精度提升1~3个数量级，运算速度提高61%。标定后解算的水平姿态角误差小于0.1°，可实现与传统标定方法相同量级的姿态精度，验证了所提方法的优越性和实用性。
Abstract:MEMS inertial measurement unit (MIMU) calibration is one of an important research direction in low-precision inertial navigation. Traditional calibration method has complex operating procedures and depends most on turntable accuracy. In order to overcome the problem of MIMU calibration in batch production, this paper presents a rapid micro-electro-mechanical system (MEMS) accelerometer calibration method based on adaptive genetic algorithm (GA), which converts calibration task to parameter optimization. Firstly, the principle of norm observation is adopted to establish the objective optimization function. Secondly, the optimal calibration scheme is designed on the basis of system observability analysis. Finally, calibration parameters can be optimized through adaptive GA with global search capability. Experimental results demonstrate that, compared with Newton's iteration, the proposed method can improve calibration accuracy by 1-3 orders of magnitude and increase operational speed by 61%. After the proposed calibration, the horizontal attitude error is less than 0.1° and its accuracy can reach the same order of magnitude as that in traditional method, which verifies its superiority and practicability.
-
航空发动机高温、高压、高载荷的工况条件使其零部件异常磨损几率相对较高，由发动机齿轮、轴承等零部件磨损造成的故障占提前换发故障的60%和空中停车故障的37.5%。航空发动机零部件异常磨损不易被及时察觉，研究在线油液监测技术，通过实时监测滑油回路中的异常大磨粒(粒径≥40 μm)监测发动机的磨损状况，对故障预警具有重要意义[1-2]。
基于静电感应原理的静电监测技术是一种有效的在线油液磨粒监测技术。发动机零部件磨损过程中产生的荷电磨粒随油液进入润滑系统中，并受油液的绝缘保护而保持荷电特性。荷电磨粒流经静电传感器时，环状或棒状电极感应区域中油液的净电荷水平变化，由此反映各个时刻流经传感器的油液中磨粒的含量[2]。但静电传感器测的是区域内所有荷电磨粒的静电场叠加值，无法获取异常大磨粒的数量、位置等信息[3]。在此基础上，静电层析成像(Electrostatic Tomography，EST)技术利用特殊的阵列式传感器获取静电信号，通过理论分析或数值计算建立电荷分布与测量数据之间的映射模型，然后求解逆问题以重建管道中电荷分布图像，由此可直观、实时地反映荷电磨粒数量、位置等信息。相对于电阻抗层析成像(EIT)，EST是被动感应式的成像，无需激励，响应速度更快，但测量值数等于电极数目，欠定性较EIT更加严重。在EST逆问题求解方面，1997年，英国的Green等[4]针对监测重力输送的双截面16电极EST系统，采用EIT中常用的线性反投影(LBP)算法重建图像并获得物料浓度。1999年，日本的Machida和美国的Scarlett设计了一套EST系统，后于2005年利用仿真实验比较了基于“Circle of Appolonius”的反投影(BP)算法和最小方差(LS)算法[5]，与直接采用EIT成像算法相比，针对EST设计的基于等势线交叠定位电荷的BP算法可准确重建不同位置的单个电荷，但难以分辨场中的2个荷电磨粒；LS算法可区分2个荷电磨粒，但空间分辨率很低。2009年，马来西亚的Rahmat等[6]将带正则化的LS(LSR)算法用于EST图像重建，并与CCD摄像机提取的颗粒分布特征比较，验证了LSR算法的准确性；2013年，他们又利用有限元法(FEM)建模，相对于LBP算法和滤波反投影(FBP)算法提高了成像质量，但空间分辨率同样受到限制[7]。国内，东南大学的研究人员将Tikhonov迭代算法用于EST图像重建[8]，后又针对浓相气固两相流提出以电容层析成像(ECT)重建图像为先验知识，排除浓度低的像素点，以提高EST的成像质量，并通过仿真实验证明了该方法的有效性[9]。2014年，Thuku和Rahmat[10]比较了4阵列传感器与16阵列传感器在电荷层析成像中的适用性，其图像重建过程采用了Landweber迭代算法。2015年，Qian和Wang等[11-12]分别研究了静电传感器在测量气力输送系统中颗粒平均流速方面的应用。浓相气固两相流中颗粒形成连续分布，l2范数正则化可取得较好的成像效果，而对于发动机气路或油路磨粒监测，监测对象本身具有稀疏性。根据NAS-1638污染度等级标准，污染度8级(即认为滑油很脏)时，100 mL油液中含50~100 μm颗粒的数目约为360[13]。本文设计的EST传感器模型中，滑油管道直径为10 mm，阵列电极轴向长度为10 mm，敏感场空间体积为0.785 mL，对应污染度8级时的大颗粒数目约为3。因此，适于选择图像向量的稀疏性为约束，并用l1范数正则化算法求解图像重建问题。2016年，Tang等[14]建立了一种半球形阵列式静电传感器模型，并分析了其空间灵敏独特性；后在此基础上，将静电传感器阵列和l1范数正则化模型用于发动机气路异常磨粒监测，并用基追踪算法重建图像，相对于l2范数正则化算法明显提高了空间分辨率[3]。
本文通过设计小尺度阵列电极传感器，并针对逆问题的严重欠定性研究了基于压缩感知理论的EST图像重建算法，以探索EST在荷电磨粒在线监测领域的应用。
1. EST数学模型
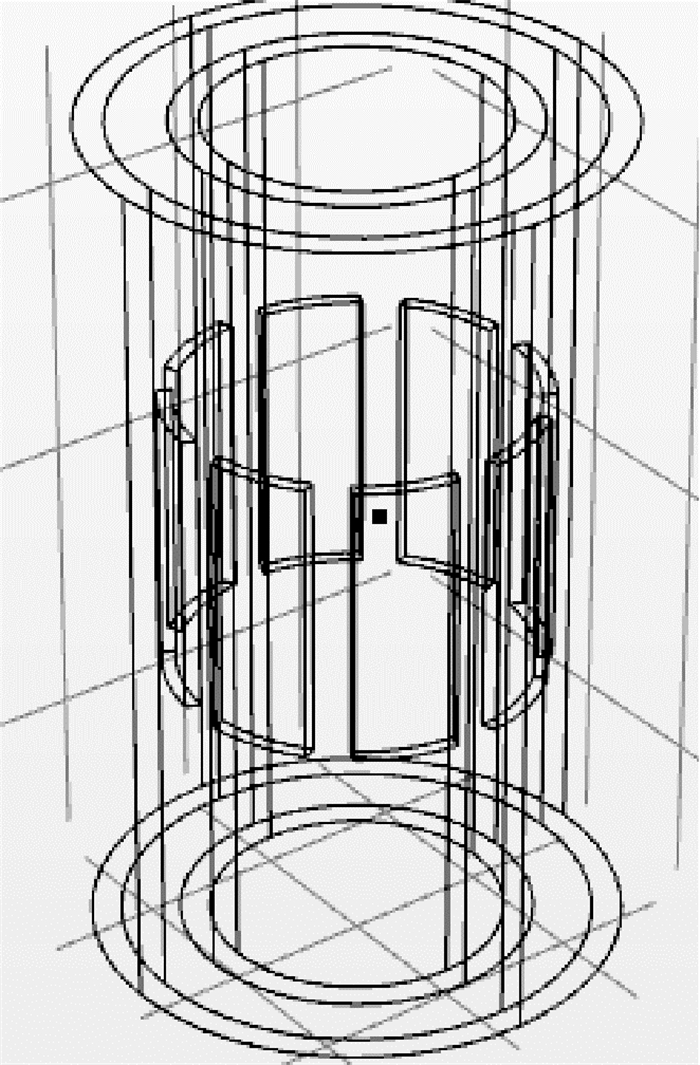
根据静电感应原理，结合滑油管道的实际尺寸，采用与小尺度8电极ECT传感器[15]类似的结构，利用有限元分析软件COMSOL建立小尺度EST传感器3D模型，如图 1所示。管道内径10 mm，为安装方便，将电极设置在管道外壁。考虑空间限制和电荷值范围，取阵列电极数目为8，增加电极数目可增加边界测量值从而提高重建精度，但会减小电极面积从而降低信噪比。可利用有限元仿真对电极尺寸进行优化。本文取电极占空比为0.9，轴向长度为10 mm。
当点电荷经过测量电极时，由于静电感应将在电极内外表面产生大小相等、符号相反的电荷。点电荷所产生的静电场与电极上感应电荷相互作用，导体达到静电平衡，此过程在极短时间内完成，因此移动点电荷与静电传感器之间的相互作用可以用静电场的Possion方程及其边界条件来描述[8]：
(1) 式中：Φ(x, y, z)为场域内的电势分布；τp为接地屏蔽罩构成的边界，电势为0；τie为与检测电路相接的阵列式电极i构成的边界，其为一等势体；ρ(x, y, z)为场域内的体电荷密度函数；ε0为真空介电常数；ε(x, y, z)为材料的相对介电常数分布；Ex为无穷远处的电场强度。
由于式(1)难以求得解析解，可用有限元法求其数值解, 得到场强分布后可求电极上的感应电量。
EST各电极上的感应电荷可表示为
(2) 式中：qi为电极i上的感应电荷值；g(x, y)为管道截面上(x, y)处的电荷值，对应重建图像中该位置的灰度值；D表示管道截面；si(x, y)为电极i在(x, y)处的灵敏度，有限元仿真中按下式计算：
(3) 其中：q(x, y)为设置于(x, y)处的点电荷电量[8]。
将式(2)离散化处理后，可得如下矩阵形式：
(4) 式中：Q为M×1维的感应电荷值向量；G为N×1维的电荷分布向量，即重建图像的灰度向量；S为M×N维的灵敏度矩阵，用于描述感应电荷值与荷电磨粒之间的映射。
为保证一定的空间分辨率，将测量截面用20×20的网格离散化，得到管道内像素单元数N=317，而测量值数等于电极数目M=8，因此，由灵敏度矩阵和感应电荷测量值求解电荷分布的逆问题具有严重欠定性。
2. EST图像重建
2.1 灵敏度矩阵预处理
2.1.1 归一化
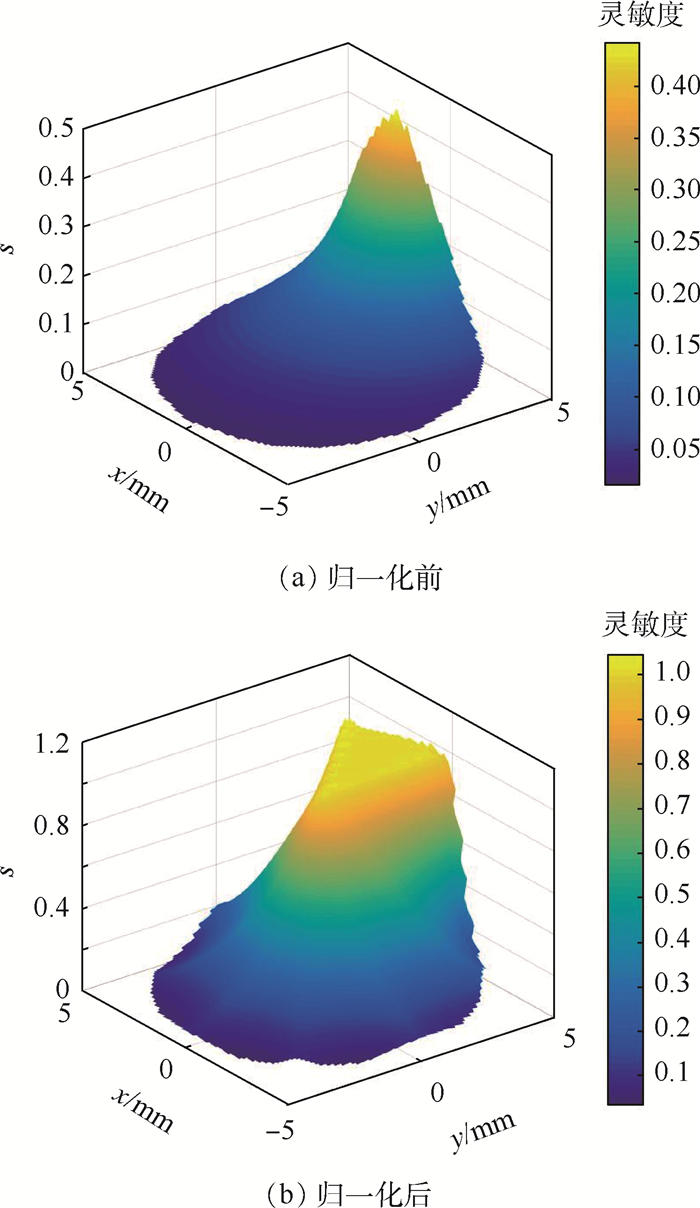
图 2(a)展示了一个测量电极对场域内全部像素点的灵敏度。可以发现，电极附近区域的灵敏度较高，即靠近管壁的区域内若存在电荷，较容易被检测到。而场域中心附近灵敏度偏低，可以认为管道中心处若出现电荷, 对传感器的输出几乎没有影响。这将导致基于灵敏度矩阵的图像重建算法对管道中央区域的分辨率低，严重影响成像质量[16]。对灵敏度系数进行归一化处理将有所改善，经仿真分析对比，对EST灵敏度矩阵设计如下归一化公式：
(5) 式中：S(i, j)为灵敏度矩阵中第i行第j列的元素；S(i, j)为归一化后的灵敏度系数；Sj为灵敏度矩阵中第j列向量。
归一化后灵敏度分布均匀性有所改善，效果如图 2(b)所示。相对于文献[8]中提出的“非等网格划分法”(即对中央区域采用较粗的剖分网格以提高灵敏度值的方法)，理论上更合理，改善效果也更好。
2.1.2 奇异值分解
压缩感知理论指出，若信号是可压缩的或在某个正交基空间中是稀疏的，就可用远低于奈奎斯特采样定理所要求的采样频率对信号进行采样并准确恢复原始信号，仅要求压缩感知矩阵满足有限等距性质(RIP)。在荷电磨粒检测中，重建目标G本身具有稀疏性，而灵敏度矩阵S是否满足RIP难以判定。为此，利用奇异值分解(SVD)对归一化后的灵敏度矩阵进行处理，将其变换为一个部分正交矩阵[3, 17-18](部分正交矩阵满足RIP性质)，以用于逆问题求解。
灵敏度矩阵S行满秩，可分解为
(6) 式中：U∈RM×M和V∈RN×N为正交矩阵；Δ=diag(δ1，δ2，…，δM)，δ1≥δ2≥…≥δM>0为S的奇异值。
令Δ*=diag(1/δ1，1/δ2，…，1/δM)，并定义Z=Δ*UTS=[IM×M 0]VT，则可按下式处理灵敏度矩阵[16]：
(7) 式中：z1，z2，…，zN为Z的列向量。
相应地，感应电荷值向量变换为
(8) 于是，EST图像重建模型变换为
(9) 式中：GSVD为对灰度向量G缩放后的向量。求解GSVD后可由下式计算G：
(10) 2.2 原始对偶内点法
针对式(9)的严重欠定性，在图像重建过程中加入稀疏性约束。根据压缩感知理论，可将EST图像重建问题转化为求式(9)的最小l1范数解问题:
(11) 本文采用原始对偶内点法(PDIPA)[19-20]求解该问题。为简单起见，对S和Q分别取灵敏度系数和感应电荷的绝对值，令GSVD是非负的。由此式(11)可转化为如下线性规划问题：
(12a) 
(12b) PDIPA法的基本思想是迭代地将不等式约束问题(11)表示为等式约束问题。首先，将原始问题(P)转化为对偶问题(D)，然后，求解原始对偶间隙，得到互补条件。问题转化为求互补条件的最优解，可通过牛顿法求解；传统的牛顿法由于计算量大不适用于大型线性规划问题，为此，研究人员开发了获取近似解的快速算法[17]，可以相对较小的计算成本获得高精度解。在迭代求互补条件最优解的过程中不断更新原始变量和对偶变量，直到满足迭代停止条件。下文图像重建中基于PDIPA法的GSVD的求解均在MATLAB平台上采用L-1 Benchmark Package实现[21-22]。
在8电极EST系统中，由于边界测量值有限，上述方法重建的电荷分布图像仍不可避免地含有伪影。例如，(x, y)处的一个点电荷在8个电极上感应的电荷值，可能与点(x, y)附近若干点电荷共同作用产生的感应电荷值相近，或者临近的2个点电荷产生的感应电荷值，与两点之间一个点电荷作用的结果相近。在不增加电极数目的前提下，为降低重建误差，将一般情况下荷电磨粒数不超过3个的先验信息融入迭代过程，即在PDIPA法每次更新变量之后，补充如下约束：
(13) 式中：Pmax为荷电磨粒数最大值；k=1，2，…，N；gPmaxt为第t次迭代中GSVDt向量中第Pmax大的元素值。
3. 仿真实验
为验证PDIPA法的有效性，利用图 1所示8电极EST传感器模型进行仿真实验。管道内径为10 mm，管内填充滑油(相对介电常数取为3)，油液中分布点电荷以表示荷电磨粒，电荷值设为10-9 C。在COMSOL 5.3和MATLAB 2016b平台上进行数值仿真，获取灵敏度矩阵和不同电荷分布情况下8个电极上的感应电荷值，用第2节方法进行图像重建，并对重建结果进行分析。计算机配置为i7-6500U CPU 2.5 GHz CPU、12 GB内存。
3.1 单个荷电磨粒的重建结果
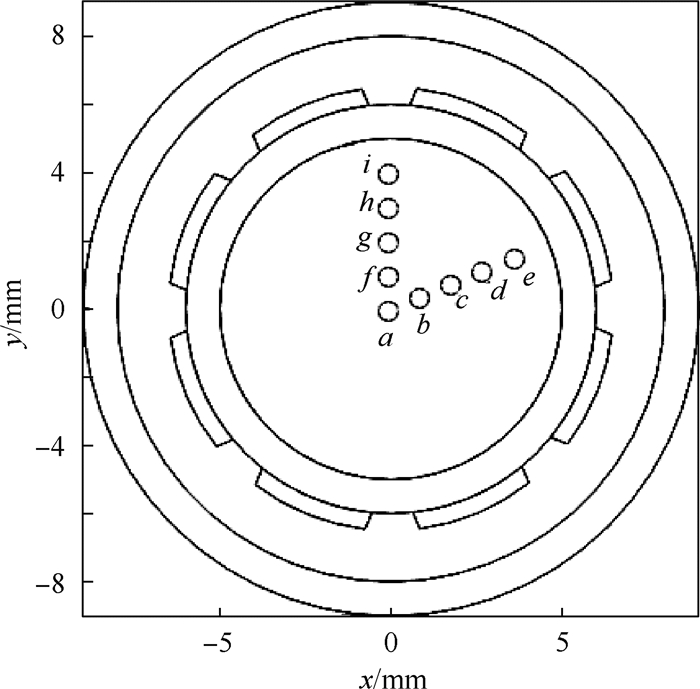
由于磨损初期异常磨粒很少，多数情况下在传感器敏感空间内可能只有一个荷电磨粒，为测试本文算法对不同位置处单个点电荷的重建效果，在测量截面上沿圆心与电极中心连线、圆心与电极空隙中心连线这2个方向上，每间隔1 mm选一个点，即在图 3所示的a~i共9个位置依次放置单个点电荷进行仿真测试。分别用基于“Circle of Appolonius”的BP算法[5]、Landweber迭代算法[23]和PDIPA重建电荷分布图像，并比较成像效果。
成像实验中，对3种算法采用相同的灵敏度矩阵归一化方法，且在BP算法中也加入了图像向量中非零元素不超过3的约束，以减少伪影。由图 4可见，BP算法对不同位置的单个点电荷可以较准确地重建，但相对于PDIPA重建的伪影较多。此外，BP算法需要设定合适的阈值，不同的检测模型需要不同的阈值，否则严重影响成像效果。在图 5所示的Landweber迭代算法重建图像中，电荷距离管道中心或边缘区域较近时，通过加入Nmax=3的约束可减少伪影，而电荷位于c、d、g、h等位置时，由于电极附近伪影像素值较大，需调大Nmax，否则无法重建出相应位置的电荷，因此图 5(c)、(d)、(g)、(h)中伪影较严重。
图 4 基于BP算法的单个电荷图像重建结果Figure 4. Image reconstruction results for single point charge based on BP algorithm
图 5 基于Landweber迭代算法的单个电荷图像重建结果Figure 5. Image reconstruction results for single point charge based on Landweber iteration algorithm由图 6所示的PDIPA图像重建结果可见，基于PDIPA的图像重建可准确获得敏感场内不同位置处的单个荷电磨粒数目与坐标，相对于图 4中BP算法和图 5中Landweber迭代算法重建的图像明显提高了成像质量。由于本文实验中剖分网格的尺寸为0.5 mm，故按网格边长的整数倍选取了实验电荷坐标，若电荷位置坐标不在剖分网格点上，将出现一定的误差，若有必要可通过进一步细化网格来改进。实时性方面，PDIPA对偶间隙的容差设为10-5，最大原始-对偶迭代次数设为50，耗时0.3 s，BP算法耗时0.003 s，Landweber迭代算法(迭代100次)耗时0.01 s，均可满足在线监测的要求。
图 6 基于PDIPA的单个电荷图像重建结果Figure 6. Image reconstruction results for single point charge based on PDIPA3.2 多个荷电磨粒的重建结果
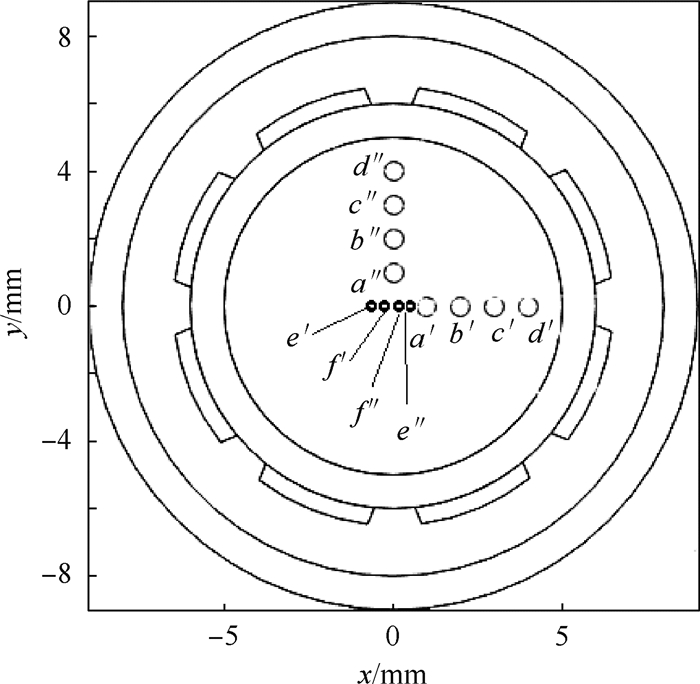
当敏感场内出现2个异常荷电磨粒时，为验证本文算法的重建效果，设计一对电荷的6组分布位置，如图 7所示。6组位置分别用a′-a″、b′-b″、c′-c″、d′-d″、e′-e″、f’-f ″表示，其坐标分别为：a′(1, 0)mm，a″(0, 1)mm，b′(2, 0)mm, b″(0, 2)mm，c′(3, 0)mm, c″(0, 3)，d′(4, 0)mm, d″(0, 4)mm，e′(-0.5, 0)mm, e″(0.5, 0)mm，f′(-0.25, 0)mm, f″(0.25, 0)mm，以上坐标位置用圆圈标记在重建截面图像上。
依次在a′-a″、b′-b″、c′-c″、d′-d″四组位置处放置2个点电荷，并分别用BP算法、Landweber迭代算法、PDIPA进行图像重建，结果如图 8~图 10所示。图 8所示的BP算法在2个及以上电荷同时存在的情况下会产生严重的伪影，无法正确判断电荷数目。由图 9(c)、(d)可见，Landweber迭代算法对相距较远的2个电荷可以由重建图像区分，当电荷位于c′-c″位置时，中心出现伪影。2个电荷进一步靠近时，如图 9(a)、(b)所示，由重建图像无法正确识别电荷数目。
图 8 基于BP算法的2个电荷图像重建结果Figure 8. Image reconstruction results for two point charges based on BP algorithm
图 9 基于Landweber迭代算法的2个电荷图像重建结果Figure 9. Image reconstruction results for two point charges based on Landweber iteration algorithm
图 10 基于PDIPA的2个电荷图像重建结果Figure 10. Image reconstruction results for two point charges based on PDIPA由图 10可见，对位于径向的不同位置、不同间距的2个荷电磨粒，采用PDIPA均可准确分辨。为进一步验证PDIPA的空间分辨能力，在间距1 mm的e′-e″位置和间距0.5 mm的f’-f ″位置分别放置电荷进行实验，结果表明，对于场域内含2个电荷的情况，在0.5 mm边长的网格剖分下，PDIPA可分辨的最小间距达到1 mm。
在发动机异常磨损的情况下，可能出现更多荷电磨粒同时流经静电传感器的情况。随着荷电磨粒数增多，8电极传感器由于测量信息有限，将难以保证重建电荷数目的准确率。下面通过测试PDIPA对3个随机分布的点电荷的重建效果，以进一步分析其可行性与局限性。用MATLAB产生10组随机整数坐标，坐标位置用圆圈标记在图 11中的管道截面图像上，以方便对比重建结果。
图 11 基于PDIPA的3个随机分布电荷图像重建结果Figure 11. Image reconstruction results for three randomly distributed point charges based on PDIPA由图 11可见，对于图 11(a)、(c)、(e)、(g)、(h)5种电荷分布情况，PDIPA对电荷数目与位置均实现了准确重建；对图 11(b)、(d)、(i)3种电荷分布模型，重建电荷位置出现偏差，但仍能正确显示电荷数目；而图 11(f)、(j)的重建图像中，2个相距1 mm的电荷图像融为一体，导致无法准确判断电荷数目。可见，随着电荷数目增加，算法的空间分辨率较2个电荷分布的情况(见图 11)有所下降。要实现对3个及以上荷电磨粒的可靠监测，需要增加测量信息。
4. 结论
在基于静电感应的荷电磨粒在线监测中，荷电磨粒数目是一个重要指标和检测难点，EST技术为实时、直观地监测荷电磨粒数提供了可行途径。EST图像重建的难点在于其测量值数目等于电极数目，用于求解逆问题的独立测量值非常有限。仿真实验表明，基于压缩感知的图像重建算法相对于传统的BP算法和EIT中常用的迭代算法可明显改善EST成像质量。
1) 基于PDIPA的图像重建可准确检测测量截面内不同位置处的单个和2个电荷，实时性满足应用要求。
2) 对于3个及以上电荷的检测，需要进一步增加测量值，以提高检测的可靠性。
3) 在3个电荷同时存在的情况下，对距离1 mm的两电荷仍实现了准确区分，说明图像重建的空间分辨率与电荷相对于测量电极的位置有关，在不增加电极数目的情况下，传感器结构仍存在优化空间，还需进一步实验研究。
-
表 1 多位置下可观测性判别矩阵的秩和奇异值
Table 1. Rank and singular value of observable matrix under multi-position
位置 秩 奇异值 3 8 29.861 29.713 29.562 29.405 29.405 29.405 4.220 2.969 1.715×10-7 4 9 41.585 41.585 41.585 29.716 29.562 29.405 6 5.168 4.198 5 9 41.585 41.585 41.585 41.585 41.585 29.564 6.708 6.708 5.968 6 9 41.805 41.585 41.585 41.585 41.585 41.585 7.348 4 7.348 4 5.968 3 7 9 51.106 46.513 41.693 41.585 41.585 41.585 7.937 2 7.819 6 6.006 3 8 9 55.280 46.533 46.513 46.493 46.493 41.657 8.374 9 8.263 3 6.033 1 9 9 59.063 55.107 50.992 46.596 46.493 46.493 8.649 9 8.394 6 6.451 9 10 9 64.408 57.427 50.991 48.495 48.261 46.572 9.154 2 9.122 3 8.204 8 11 9 68.476 58.829 55.023 50.931 50.931 47.303 9.882 8 9.832 8 9.463 6 12 9 72.041 65.751 58.810 51.012 50.931 50.931 10.392 10.392 9.881 7 13 9 72.041 67.576 58.813 58.810 52.764 50.951 10.816 10.765 10.605 14 9 72.041 68.973 62.385 62.377 55.011 55.011 11.178 11.149 11.132 15 9 72.041 68.973 65.779 62.394 62.394 62.377 11.458 11.456 11.439 
下载: 导出CSV
表 2 本文方法与牛顿迭代法的标定结果对比
Table 2. Comparison of calibration results between proposed method and Newton's iteration
误差参数 传统标定方法标定结果 牛顿迭代法 本文方法 标定结果 相对误差/% 标定结果 相对误差/% Bx/(m·s-2) 0.116 46 0.116 29 -0.146 0.116 44 -0.017 By/(m·s-2) 0.036 1 0.035 9 -0.554 0.036 107 0.019 Bz/(m·s-2) 0.136 44 0.138 42 1.451 0.136 37 -0.051 Sxx 9.805 18 9.805 2 0.000 204 9.805 9 0.007 Syy 9.787 18 9.788 2 0.010 4 9.787 6 0.004 Szz 9.771 07 9.811 5 0.414 9.771 1 0.000 3 Mxy -0.005 8 0.276 8 × -0.006 42 10.69 Mxz 0.005 22 0.405 1 × 0.002 42 -53.64 Myx 0.006 07 —— —— —— —— Myz 0.003 93 -0.768 9 × 0.003 09 -21.37 Mzx -0.003 6 —— —— —— —— Mzy -0.006 2 —— —— —— —— 注：“×”表示无相对误差结果；“——”表示无此项安装误差。
下载: 导出CSV
表 3 本文方法与牛顿迭代法的运算时间对比
Table 3. Comparison of operational time between proposed method and Newton's iteration
方法 运算时间/s 本文方法 164.28 牛顿迭代法 421.92
下载: 导出CSV
表 4 水平姿态角误差均值
Table 4. Mean of horizontal attitude errors
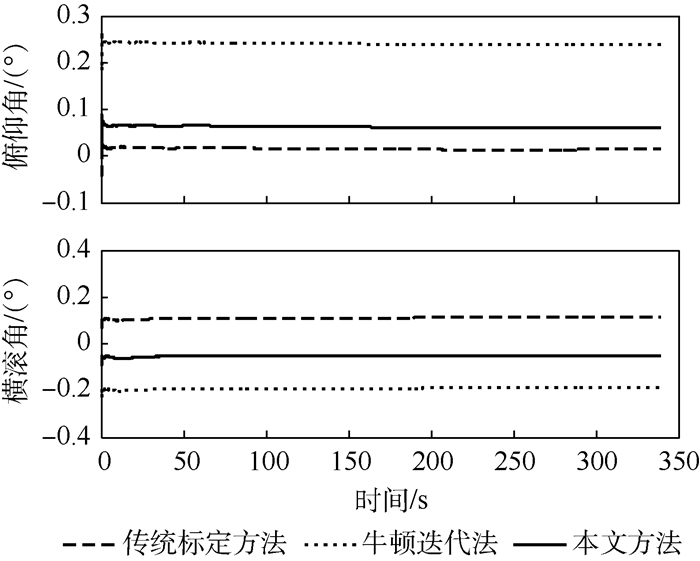
方法 俯仰角误差/(°) 横滚角误差/(°) 传统标定方法 0.015 0.109 牛顿迭代法 0.24 -0.191 本文方法 0.062 -0.051
下载: 导出CSV
-
[1] 尹文.MIMU微惯性测量单元误差建模与补偿技术[D].长沙: 国防科学技术大学, 2007: 1-2.YIN W.Error modeling and compensation of micro inertial measurement unit[D].Changsha: National University of Defense Technology, 2007: 1-2(in Chinese). [2] 王如胜.MEMS陀螺捷联惯导系统标定方法研究[D].哈尔滨: 哈尔滨工业大学, 2015: 1-6.WANG R S.Research on the calibration method of MEMS gyro strapdown inertial navigation system[D].Harbin: Harbin Institute of Technology, 2015: 1-6(in Chinese). [3] LÖTTERS J C, SCHIPPER J, VELTINK P H, et al.Procedure for in-use calibration of triaxial accelerometers in medical applications[J].Journal of Applied Behavior Analysis, 1998, 68(1-3):221-228. [4] FROSIO I, PEDERSINI F, BORGHESE N A.Autocalibration of MEMS accelerometers[J].IEEE Transactions on Instrumentation and Measurement, 2009, 58(6):2034-2041. doi: 10.1109/TIM.2008.2006137 [5] WON S P, GOLNARAGHI F.A triaxial accelerometer calibration method using a mathematical model[J].IEEE Transactions on Instrumentation and Measurement, 2010, 59(8):2144-2153. doi: 10.1109/TIM.2009.2031849 [6] FONG W T, ONG S K, NEE A Y C.Methods for in-field user calibration of an inertial measurement unit without external equipment[J].Measurement Science & Technology, 2008, 19(8):817-822. doi: 10.1088-0957-0233-19-8-085202/ [7] 戴邵武, 王克红, 戴洪德.基于PSO算法的加速度计快速标定方法[J].电光与控制, 2014, 21(12):57-60. doi: 10.3969/j.issn.1671-637X.2014.12.013DAI S W, WANG K H, DAI H D.A rapid calibration method for accelerometer based on PSO algorithm[J].Elctronics Optics & Control, 2014, 21(12):57-60(in Chinese). doi: 10.3969/j.issn.1671-637X.2014.12.013 [8] 杨管金子, 李建辰, 黄海.基于遗传算法的加速度计免转台标定方法[J].中国惯性技术学报, 2017, 25(1):119-123.YANG G J Z, LI J C, HUANG H.Non-turntable calibration method for three-accelerometer based on genetic algorithm[J].Journal of Chinese Inertial Technology, 2017, 25(1):119-123(in Chinese). [9] 张红良.陆用高精度激光陀螺捷联惯导系统误差参数估计方法研究[D].长沙: 国防科学技术大学, 2010: 39-40.ZHANG H L.Research on error parameter estimation of land high-precision ring laser gyroscope strapdown inertial navigation system[D].Changsha: National University of Defense Technology, 2010: 39-40(in Chinese). [10] 葛继科, 邱玉辉, 吴春明, 等.遗传算法研究综述[J].计算机应用研究, 2008, 25(10):2911-2916. doi: 10.3969/j.issn.1001-3695.2008.10.008GE J K, QIU Y H, WU C M, et al.Summary of genetic algorithms research[J].Application Research of Computers, 2008, 25(10):2911-2916(in Chinese). doi: 10.3969/j.issn.1001-3695.2008.10.008 [11] DU Y, FANG J, MIAO C.Frequency-domain system identification of an unmanned helicopter based on an adaptive genetic algorithm[J].IEEE Transactions on Industrial Electronics, 2013, 61(2):870-881. [12] MATIAS T, SECO R, BELCHIOR C.Automatic extraction of the fuzzy control system by a hierarchical genetic algorithm[J].Engineering Applications of Artificial Intelligence, 2014, 29(3):70-78. [13] SU L M, HOU C Z, DAI Z J, et al.Application of improved genetic algorithm in network fault diagnosis expert system[J].Journal of Beijing Institute of Technology, 2003, 12(3):225-229. [14] 管小艳.实数编码下遗传算法的改进及其应用[D].重庆: 重庆大学, 2012: 4-5.GUAN X Y.Improvement and application of genetic algorithm under real number coding[D].Chongqing: Chongqing University, 2012: 4-5(in Chinese). [15] 张思才, 张方晓.一种遗传算法适应度函数的改进方法[J].计算机应用与软件, 2006, 23(2):108-110. doi: 10.3969/j.issn.1000-386X.2006.02.044ZHANG S C, ZHANG F X.A modified method to fitness function of genetic algorithms[J].Computer Applications and Software, 2006, 23(2):108-110(in Chinese). doi: 10.3969/j.issn.1000-386X.2006.02.044 [16] SRINIVAS M, PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(4):656-667. doi: 10.1109/21.286385 [17] 卢兆兴, 张金生, 王仕成, 等.基于自适应遗传算法的三轴磁强计误差校正方法[J].传感技术学报, 2014, 27(3):331-336. doi: 10.3969/j.issn.1004-1699.2014.03.011LU Z X, ZHANG J S, WANG S C, et al.Calibration for tri-axial magnetometer based on adaptive genetic algorithm[J].Chinese Journal of Sensors and Actuators, 2014, 27(3):331-336(in Chinese). doi: 10.3969/j.issn.1004-1699.2014.03.011 [18] 丁智坚.三轴惯性/地磁组合测量系统标定方法研究[D].长沙: 国防科学技术大学, 2012: 36-40.DING Z J.Research on the calibration method of inertial/geomagnetic integrated measurement system[D].Changsha: National University of Defense Technology, 2012: 36-40(in Chinese). -
下载:
下载:
点击查看大图
计量
- 文章访问数: 929
- HTML全文浏览量: 134
- PDF下载量: 421
- 被引次数: 0
