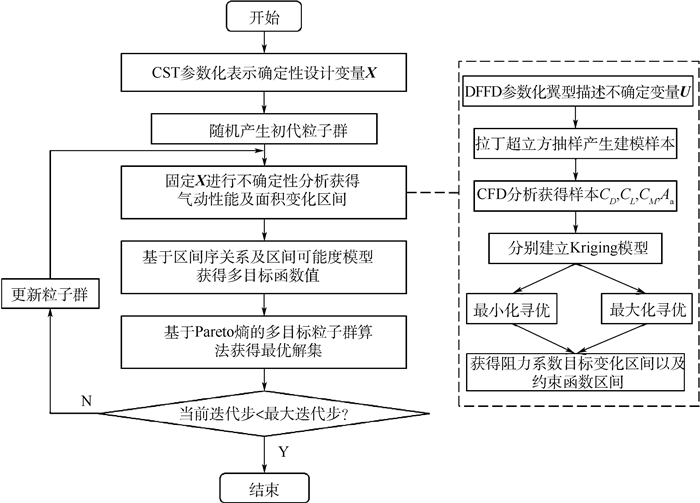
Interval analysis for geometric uncertainty and robust aerodynamic optimization design
-
摘要:
不确定性因素会导致飞行器偏离预先设计的气动性能,造成气动性能下降甚至产生严重的后果。针对工程中无法给出准确的几何不确定性概率分布以及跨声速条件下非线性气动问题,对几何不确定性的非概率参数化建模进行了研究,并结合Kriging模型及最优化方法建立了快速非线性区间分析方法。采用该方法对对称翼型进行不确定性分析,获得了气动性能参数的定量变化区间。在区间不确定性分析基础上建立了鲁棒优化设计流程。基于区间序关系及区间可能度转换模型将单目标区间不确定性优化问题转化为多目标确定性优化问题,并采用基于Pareto熵的自适应多目标粒子群算法对优化问题进行寻优。考虑几何不确定性以及升力、力矩、面积约束,以阻力性能为目标对超临界翼型进行了鲁棒优化设计。与确定性优化设计结果对比表明,确定性优化设计在不确定性因素的影响下易失效,而鲁棒设计可得到更安全可靠的结果。
-
关键词:
- 几何不确定性 /
- 非线性区间分析 /
- 直接操作自由变形(DFFD) /
- 气动优化设计 /
- 鲁棒优化设计 /
- 自适应多目标粒子群算法 /
- Kriging模型
Abstract:Uncertainties will make aircraft deviate from the designed aerodynamic performance, resulting in the decrease in aerodynamic performance and even destruction. Due to the problem that the probability distribution of geometric uncertainty cannot be given in engineering and nonlinear aerodynamic problem in transonic flows, the non-probabilistic parametric modeling of geometric uncertainty is studied, and the fast nonlinear interval analysis method is established in combination with Kriging model and optimization method. The effects of geometric uncertainties on a symmetric airfoil are analyzed using the above method, and the quantitative variation range of aerodynamic performance is obtained. Based on interval uncertainty analysis, a robust optimization design process is established. The single-objective interval uncertainty optimization problem was transformed into deterministic multi-objective optimization problem based on the order relation and possibility degree model of interval number, and the optimization problem was solved by adaptive multi-objective particle swarm optimization which is based on Pareto entropy. The robust optimization design is implemented for the supercritical airfoil with the drag objective as well as lift, moment and area constraints under geometric uncertainties. The results compared with deterministic optimization design show that deterministic design is prone to failure under the influence of uncertainties, while the robust design is more secure and reliable.
-
航空航天工业中,飞行器设计的各参数往往被看作确定的量,但实际上,工程中是无法避免不确定性存在的。例如飞行器结构设计由于制造水平、测量误差等会造成参数的不确定性,飞行器飞行环境及载荷作用也会存在更强的不确定性等[1]。不确定性因素严重影响了与其相对的确定性设计的精度和可靠度,因此,想要获得更可靠更稳定的设计,必须考虑不确定性因素的影响。考虑不确定性的设计方法主要包括鲁棒(稳健)优化设计方法[2]及可靠性优化设计方法[3]。鲁棒优化设计旨在降低飞行器性能对不确定因素的灵敏度,而可靠性设计旨在降低发生故障或失效的概率,提高飞行器的可靠性。本文主要研究翼型的鲁棒优化设计方法。
与传统的确定性优化相比,鲁棒优化设计需要在优化过程中不断进行不确定性分析。其主要包括概率方法和非概率方法。概率方法又包括蒙特卡罗(Monte Carlo)方法、泰勒展开、随机展开等,如徐明等[4]采用蒙特卡罗方法对旋翼的最优转速进行了不确定性分析;Salehi等[5]和邬晓敬等[6]采用非浸入式混沌多项式方法对离心泵的流场及翼型跨声速随机气动特性等分别进行了不确定性分析;戴玉婷和杨超[7]考虑广义刚度的随机不确定性,基于浸入式随机展开方法分析了不确定性对颤振边界的影响;Papadimitriou等[8]考虑流动相关参数及几何不确定性,并采用离散网格技术进行不确定性分析,对阻力系数目标进行了鲁棒优化设计。概率方法一般要事先给定不确定性变量的概率分布函数,但是工程中很难获得充足的样本来估计分布函数的参数或验证概率分布函数的合理性,而人为假设又会导致较大的分析误差[9],相比之下获得不确定性因素的取值范围较容易,因此研究人员发展了“基于边界表征”的非概率不确定性方法,其中区间分析方法应用较多。屈小章等[10]采用区间方法描述风机翼型的几何不确定性变量,对其气动性能进行了稳健优化设计;Zheng和Qiu[11]采用区间分析的方法对考虑不确定性的气动力和气动热进行了分析;张军红和韩景龙[12]提出了一种考虑区间不确定性的机翼颤振优化方法。
飞行器生产时本身存在制造误差,在飞行过程中也会由于载荷的作用以及结冰、烧蚀等现象使飞行器气动外形产生局部变化,进而影响气动性能。另外,飞行器跨声速飞行时,流场具有强非线性,几何外形变化对气动性能的影响会更大、更复杂。以往研究中,对几何不确定性变量或采用假设的概率方法描述[8, 13],容易造成较大的分析误差;或采用基于特征几何参数的区间描述[10-11],无法表达翼型任意的局部变化。且大多数非概率方法研究均基于区间数运算分析方法,该方法适用于分析函数在不确定区间内为单调函数的情况,不适用于复杂的非线性气动问题。
针对以上问题,本文研究了几何不确定性的通用区间描述及快速非线性区间分析方法。在此基础上建立了鲁棒优化设计流程,并通过标准算例验证了方法的有效性。
1. 区间不确定性分析
1.1 直接操作自由变形参数化方法
采用区间方法进行几何不确定性分析,首先要通过合适的参数化方法建立翼型几何不确定性的区间描述。工程中现已发展出多种翼型参数化方法[14],如类别形状函数变换(Class Shape Transformation, CST)方法、Hicks-Henne型函数法、PARSEC方法、B样条法等。上述方法或通过间接变量描述翼型,或通过如前缘半径、最大厚度位置等特征参数描述,但均无法直接控制翼型上某点的变化,不能灵活表达翼型表面凹凸等局部变形,故不适合描述任意的几何不确定性。本文采用直接操作自由变形(DFFD)方法[15]对翼型参数化,以翼型表面点的直接变形为参数建立几何不确定性量区间描述。
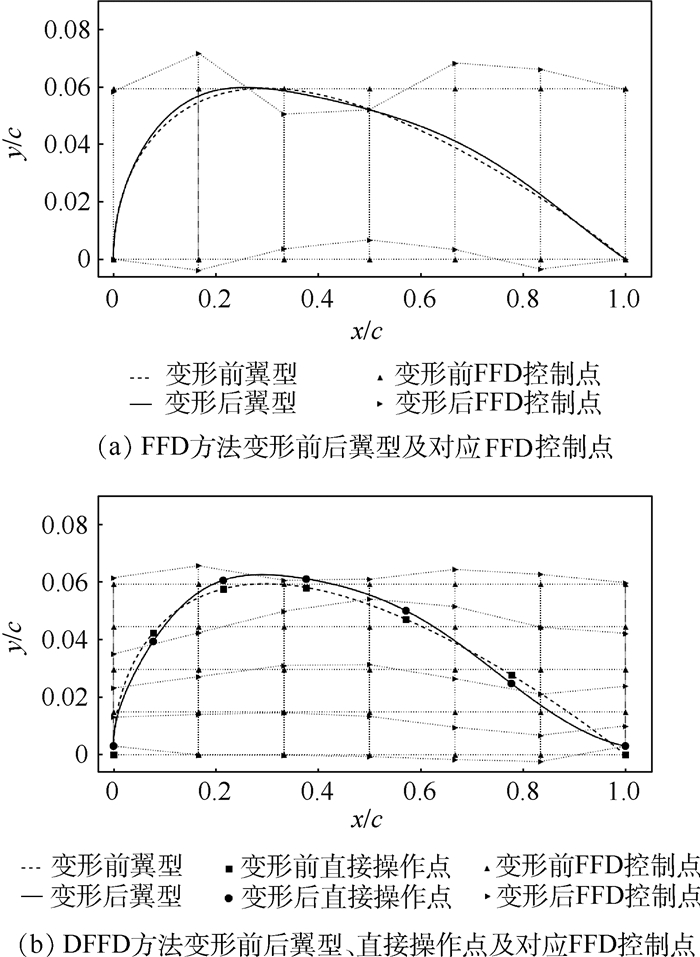
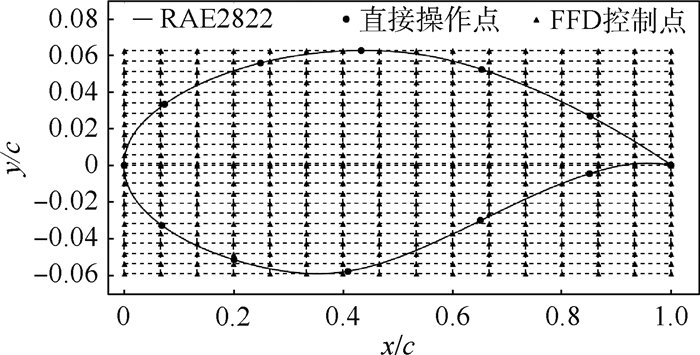
对于一般自由变形(FFD)方法,首先在变形物体周围布置控制体,如图 1(a)所示,图中,x/c为弦向位置, y/c为纵向位置,x、y分别为实际弦向及纵向坐标,c为翼型弦长。然后定义变形物体上各点实际坐标关于局部坐标的函数为

(1) 式中:l、m、n为FFD控制体3个方向的阶数;Pi, j, k为FFD控制点的坐标;

在定义的局部坐标系中,若FFD控制点的位移量为ΔPi, j, k,相应可得变形物体上各点的位移量为

(2) 则变形物体上各点的最终位置为

(3) FFD方法虽然变形简单,但变形物面的点和FFD控制点并没有直观的联系,无法通过FFD控制点的变形精确控制物面某点的变形。DFFD方法在FFD方法的基础上发展而来,其不同于一般FFD方法的是除在翼型周围布置控制体和控制点外,在翼型上也布置直接操作点(pilot points)。通过直接操作点的位移反求FFD控制体上控制点的位移,进而通过FFD方法控制翼型的变化。由于将直接操作点的位移作为控制参数,因此可以使用高阶的FFD控制体而不增加变量维数。反求的过程可看作求解满足直接操作点位移约束的FFD控制点的位移组合,假设直接操作点的位移相互独立,Sf(f=1, 2, …, h)为变形前直接操作点的原始坐标,Tf(f=1, 2, …, h)为变形后各直接操作点的坐标。由式(2)可得

(4) 式中:δi, j, k为待求的FFD控制点的位移。
一般情况下,直接操作点的个数小于FFD控制点的个数,故式(4)可能有多个解,此处采用最小二乘法求解,即找到一组解使

1.2 非线性区间分析方法
区间分析方法[16]采用区间数学的概念,将每一维不确定量v表示为区间形式:

(5) 式中:上标I、L、R分别表示区间、区间下界、区间上界。由区间2个端点组成的一对有序实数称为区间数。区间数的中值记作AC=(AL+AR)/2,区间半径或离差记作Aw=(AR-AL)/2。
普通的线性区间函数问题可以通过区间数运算以及区间扩张获得关于自变量的区间函数值,但跨声速条件下的气动问题属于复杂的非线性问题,且没有显式的函数关系。本文通过优化方法进行非线性区间分析,即采用单目标粒子群进化算法,分别进行最大化目标、最小化目标共两次寻优获得目标函数区间的上界和下界。
除采用直接优化进行不确定分析外,本文同时采用构建代理模型结合优化方法进行不确定分析,以提高效率。本文选择具有优异的非线性函数近似能力的Kriging模型[17]作为代理模型,建立不确定变量与气动性能参数的函数关系。即通过拉丁超立方设计在不确定性变量取值空间选取一定量样本并进行CFD计算,通过样本集建立Kriging模型,对模型分别进行最大最小化目标寻优。为进一步提高代理模型精度,在初始样本的基础上采用最大均方差准则(MSE)进行加点,即选取当前模型在建模空间内预测均方差最大的点进行精确CFD分析并加入到样本集内,重新构建代理模型。
1.3 不确定性分析算例
本文针对NACA0012翼型,进行了考虑几何不确定性的阻力性能分析。为简化问题,考虑不确定性时仍保证翼型对称。首先采用DFFD方法对上半翼型进行参数化,建立10×8阶FFD控制体,并在翼型上选取7个直接操作点,其弦向位置如表 1所示。为保证前后缘固定,首尾2个直接操作点固定,改变其余5个直接操作点的y向位移以控制翼型变化,因此共有5个不确定性变量,其变化范围均为[-0.001 5, 0.001 5]。采用粒子群算法优化求解时,除粒子的位置和速度约束在变化范围内,无其他约束。
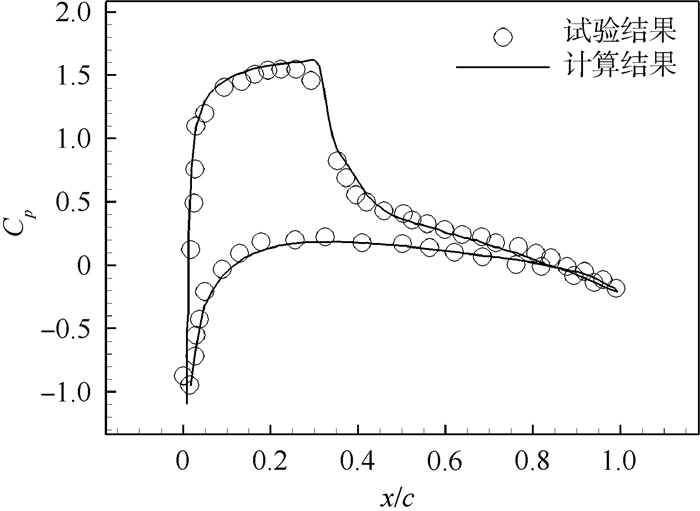
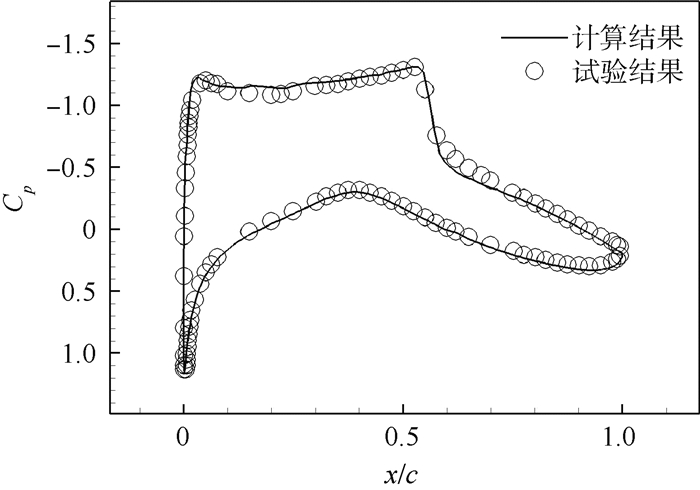
表 1 直接操作点x方向位置Table 1. Position of pilot points in x direction序号 x/c 1 0 2 0.077 3 0.214 4 0.377 5 0.571 6 0.777 7 1.0 翼型的阻力预测采用课题组自主研发的基于Navier-Stokes方程的并行CFD求解器[18],湍流模型采用k-ω两方程模型,空间离散采用二阶格式,时间推进采用LU-SGS方法,网格采用美国国家航空航天局(NASA)提供的449×129标准网格。图 2为马赫数0.7、迎角4°、雷诺数4.06×106条件下,计算压力系数Cp分布与试验数据[6]的比较,计算精度可满足要求。
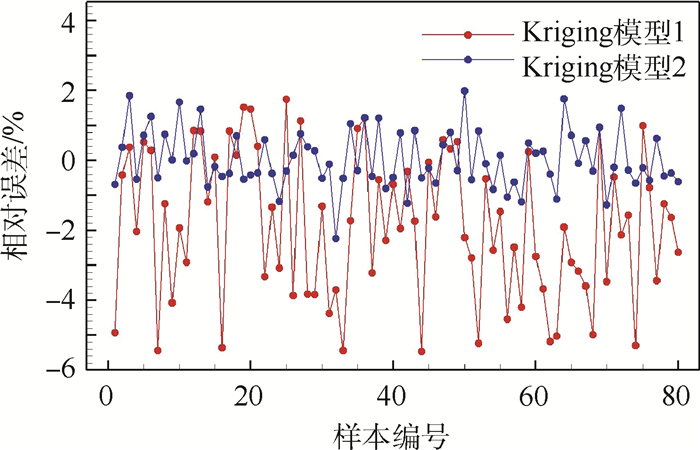
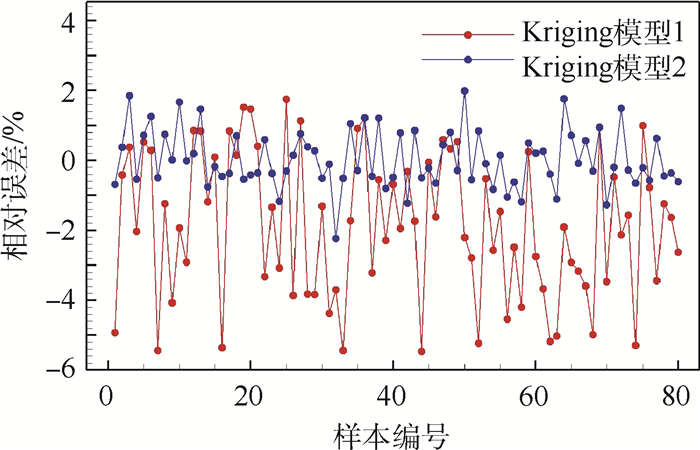
不确定分析算例采用工况为迎角0°,马赫数0.85,该条件下计算得阻力系数为0.0538。首先采用20个初始样本建立了阻力系数与不确定变量的Kriging模型(Kriging模型1)。在此基础上又加点7次,重新构建模型(Kriging模型2)。在不确定性变化区间内随机选取80个样本使用模型进行预测并采用精确CFD分析进行验证,以检验代理模型精度,样本阻力系数的相对误差如图 3所示,采用20个初始样本建立代理模型,相对误差最大为5.47%,加点7次后,最大相对误差减小为2.24%,该精度可以满足工程应用。
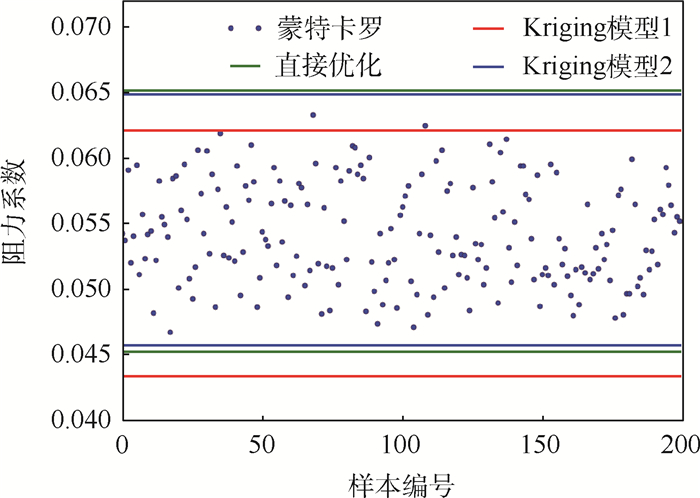
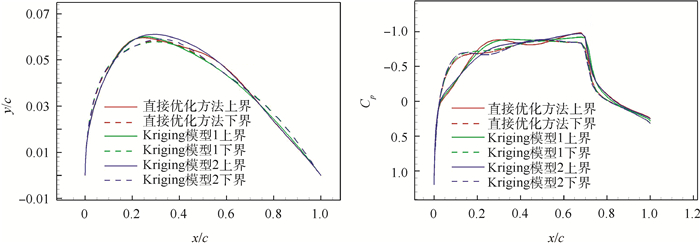
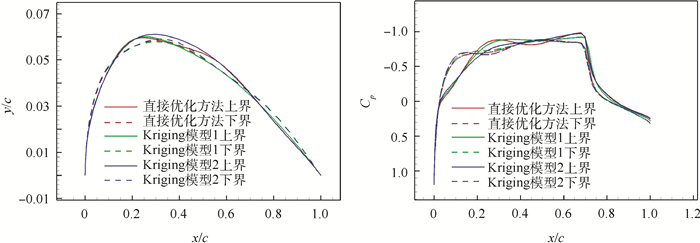
为验证不确定性分析的准确性,采用蒙特卡罗方法进行不确定性分析,即在设计空间内选取200个随机样本进行精确CFD分析并统计,并与上述3种结果对比,直接优化、Kriging模型优化与蒙特卡罗方法结果比较如图 4所示。结果表明直接优化方法具备较高的精度,只通过20个初始样本构建Kriging模型,得到的结果与直接优化结果存在一定误差,通过加点重建Kriging模型,误差进一步减小。直接优化中每一步所有CFD分析可并行进行,建立代理模型的20个初始样本也可并行进行CFD分析,但加点过程无法并行进行,故3种方法的分析结果、相对误差、CFD计算次数、并行计算时间比较如表 2所示。其中,采用Kringing模型1最大相对误差小于5%,而分析效率可提高95%。3种方法得到的阻力系数变化区间上下界对应的翼型及压力分布如图 5所示,由图中可以看出,各方法得到的翼型相似。
表 2 3种方法的分析结果、误差、CFD计算次数、计算时间比较Table 2. Comparison of analysis results, errors, CFD calculation times and computing time among three methods方法 最大阻力系数 最大阻力系数相对误差/% 最小阻力系数 最小阻力系数相对误差/% CFD计算次数 并行计算时间/min 直接优化 0.0651303 0.0452392 800 500 Kriging模型1 0.0620658 -4.70 0.0433786 -4.10 20 25 Kriging模型2 0.06480712 -0.49 0.0457063 1.03 27 200 2. 鲁棒优化设计
2.1 优化算例
本文采用RAE2822翼型优化设计标准算例,流场求解采用前述的CFD求解器。优化问题描述为

(6) 式中:CD为阻力系数目标;X为描述翼型几何的n维设计变量;V为设计空间;考虑升力系数CL、俯仰力矩系数CM以及面积Aa约束,Ainitial为RAE2822翼型的面积,大小为0.077 873。计算工况为马赫数0.734,雷诺数6.5×106。图 6为迎角2.79°条件下该翼型的计算与试验压力分布比较结果。
首先对该问题进行传统的确定性优化。通过试验,采用DFFD方法对翼型进行参数化时,若参数的变化范围较大,极易使翼型产生大的波动,从而不具备翼型的基本几何特征,类似问题也出现在其他直接以物面点位移参数化的方法中[19]。因此,DFFD方法虽可以直接控制翼型表面变形,但并不适合较大空间内的翼型参数化建模,故本文采用CST方法对翼型进行参数化,作为确定性的设计变量,翼型上下部分分别采用5阶CST参数化。由于进行CFD计算时直接改变迎角进行定升力计算,因此假设升力系数等式约束直接成立,实现时,给定阈值[0.823, 0.825],检测升力系数稳定收敛到阈值内结束计算。不等式约束处理采用罚函数法,约束函数值计算式为

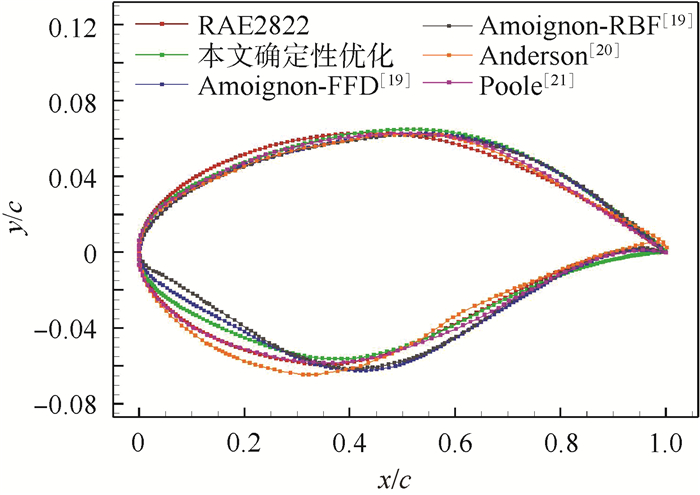
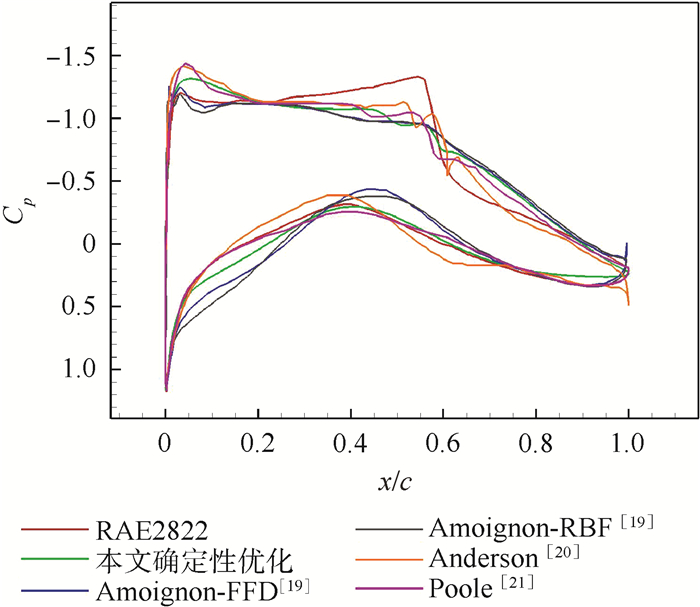
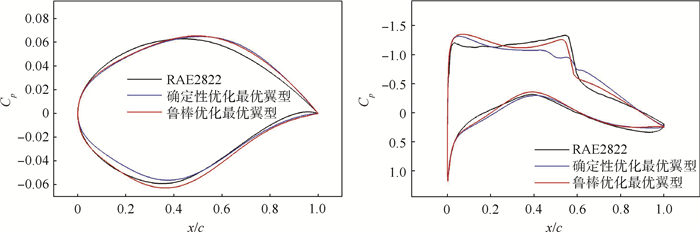
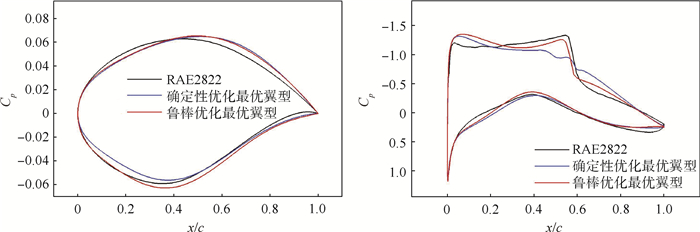
(7) 优化算法采用单目标粒子群算法,优化结果以及RAE2822翼型计算结果如表 3所示,α为迎角。对本文的优化结果与其他文献[19-21]进行了对比,数值结果如表 4所示,图 7为优化后的翼型对比,图 8为优化后压力分布对比,本文优化后阻力系数下降35.9%,且满足各项约束。与其他文献结果对比,在基本相同的设计变量个数下,本文取得了较好的结果。
表 3 RAE2822翼型及优化翼型的计算结果Table 3. Computing results of RAE2822 and optimized airfoils翼型 CD α/ (°) CL CM Aa RAE2822 0.02112 2.75377 0.82489 -0.1023 0.07787 优化翼型 0.01354 2.84263 0.82449 -0.0916 0.07804 2.2 鲁棒优化设计方法
在2.1节算例的基础上考虑翼型几何的区间不确定性,问题(6)可描述为

(8) 式中:U为q维不确定向量,用q维区间向量UI表示。目标函数和约束函数均为不确定变量U的连续函数,故其可能取值也构成区间形式,而不是确定值,因此,上述问题无法通过传统的确定性优化方法求解。
鲁棒优化设计中,将不确定性变量导致的目标性能区间作为设计目标,因此在优化过程中,需比较不同样本的目标性能区间的大小。本文中,利用≤Cw区间序关系[16]比较2个区间AI和BI的大小,对于最小化问题其定义如下:

区间约束函数采用区间可能度模型转换为确定性约束函数。对于形如gi(X, U)≤biI的区间不确定性约束,可转换为如下确定不等式约束:

(9) 式中:giI(X)为约束函数gi(X, U)在X处由不确定性造成的可能取值区间;biI为不确定约束的区间约束值;0≤λi≤1为一预先给定的可能度水平。式(9)表示函数giI(X)满足约束的可能度即概率不小于给定的可能度水平。“≥”型不等式约束以及等式约束均可转换为“≤”型不等式约束再计算可能度。根据两区间的所有可能位置关系,具体的区间可能度模型如式(10),当某一区间退化为实数时,仍然适用。

(10) 通过以上区间序关系以及基于区间可能度的约束转换方法,单目标优化问题(8)可转换为以阻力性能区间中值CDC和半径CDw为目标的多目标优化问题(11),即

(11) 如2.1节所述,升力系数等式约束自动满足,其他约束采用罚函数法处理,则问题(11)进一步转换为无约束优化问题:

(12) 式中:

本文基于区间不确定性分析方法及自适应多目标粒子群算法,建立了考虑几何区间不确定性的鲁棒优化设计方法,求解上述优化问题,其流程如图 9所示。
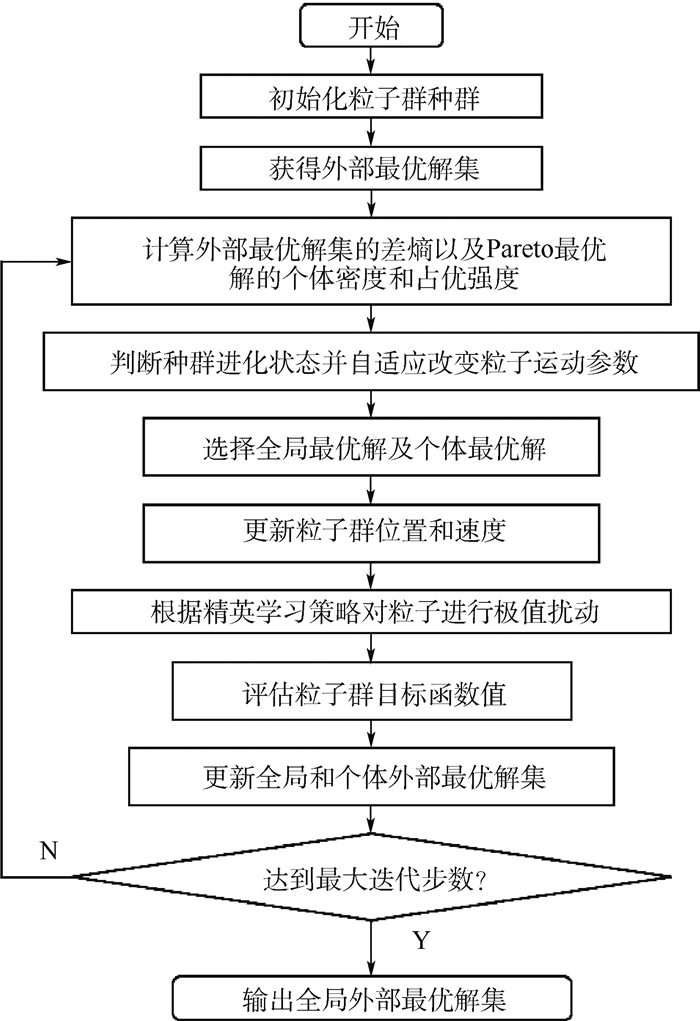
2.3 自适应多目标粒子群算法
本文采用粒子群算法具有形式简洁、收敛快速以及参数调节机制灵活等优点。在粒子群算法中,一个粒子i可由位置向量xi=[xi, 1, xi, 2, …, xi, d]T∈Rd和速度向量vi=[vi, 1, vi, 2, …, vi, d]T∈Rd表示,其中i=1, 2, …, N,N为种群中的粒子个数,d为设计变量的维数。粒子在进化过程中根据式(13)更新速度和位置:

(13) 式中:t为迭代次数;ω≥0为惯性权重;c1、c2为加速系数;r1、r2为在[0, 1]上均匀分布的随机数;pbesti为第i个粒子的历史个体最优解; gbest为群体的全局最优解。为避免陷入局部最优,可采用精英学习策略进行局部极值扰动,精英学习率为Lr。本文自适应多目标粒子群算法基于Pareto占优原则建立并维护外部最优解集,通过引入Pareto熵表示Pareto前缘的分布均匀性,间接表示种群的多样性。优化迭代时,Pareto前缘发生变化,相应的Pareto熵也发生变化,故可以采用差熵表示Pareto前缘重新分布范围的大小,通过差熵可以推测当前种群发现新解的能力,估计种群所处的进化状态包括收敛状态、多样化状态及停滞状态,进而调整参数ω、c1、c2、Lr以设计适应当前状态的勘探和开采策略。
优化算法的具体流程如图 10所示,文献[22]采用此优化算法对不同测试算例进行了验证,并与其他常用多目标优化算法进行了对比,结果显示该算法总体上具有更好的多样性和收敛性。
2.4 结果分析
采用2.2节鲁棒优化设计方法对问题(12)优化。几何不确定性变量仍采用DFFD方法参数化产生,对超临界翼型的上半部分和下半部分分别进行参数化,各布置7个直接操作点,采用16×12阶控制体,直接操作点及控制体建立如图 11所示。翼型前缘和后缘的直接操作点仍保持固定,故共10个不确定性变量,变化区间仍为[-0.0015, 0.001 5]。为提高计算效率,对计算精度与计算时间进行折中,选取通过25个初始样本构建Kriging模型的方式进行阻力系数及力矩系数的不确定性分析,直接优化的方式进行翼型面积的不确定分析。代理模型精度校验得阻力系数预测的最大误差为7.4%,力矩系数预测的最大误差为0.63%。多目标优化所得Pareto解集如图 12所示。
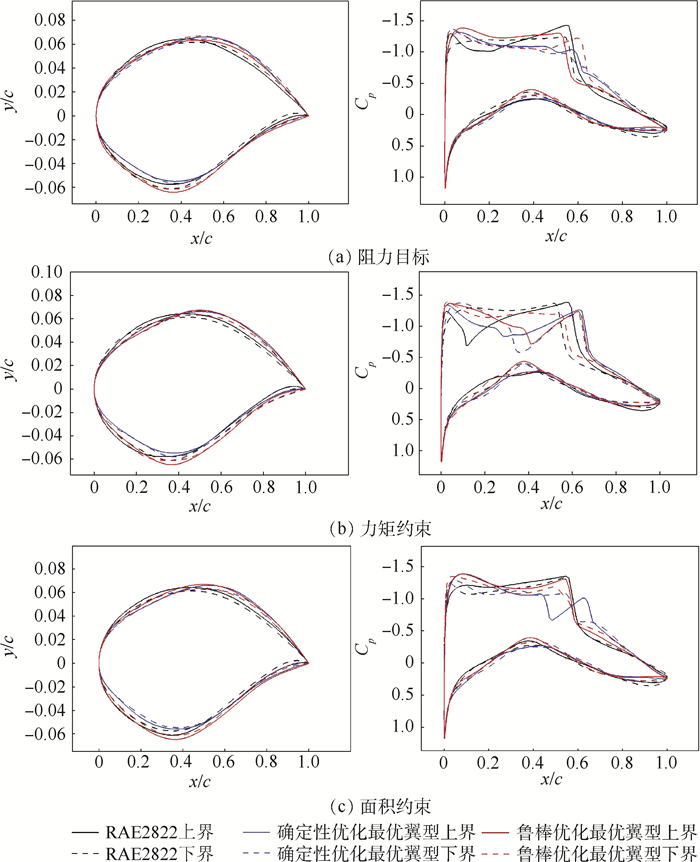
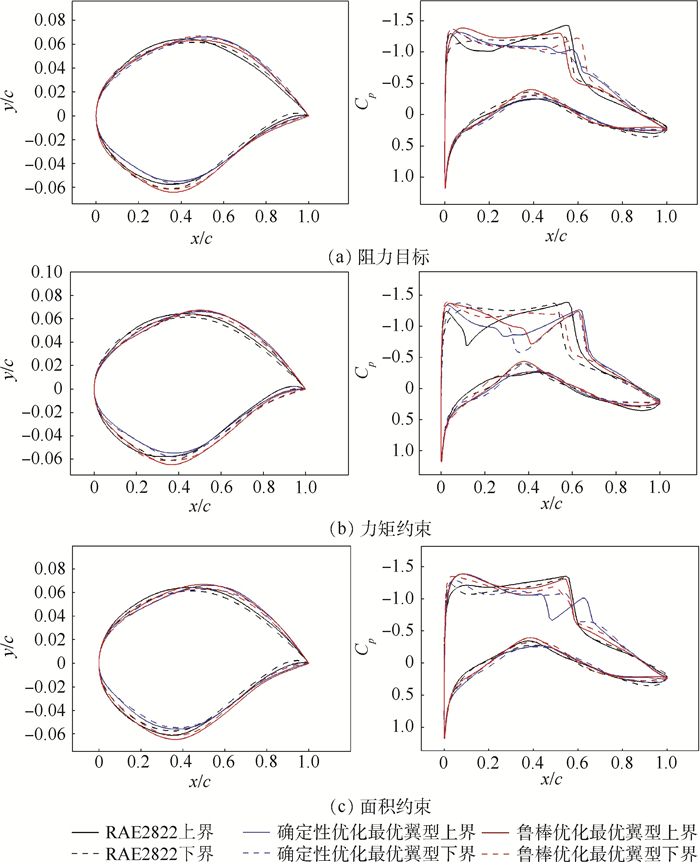
由于多目标优化中粒子群容量及进化步数设置较小,且跨声速问题机理复杂,所得的Pareto前缘不甚明显,但工程中只需选取一个或几个最优解即可,故选取图中Pareto前缘的一点作为本次鲁棒优化的最优解,并对最优翼型进行CFD分析,得其阻力系数CD;同时采用相同的参数化及代理模型建立方法对确定性优化得到的最优翼型及初始RAE2822翼型进行一次不确定性分析,其相关数值如表 5所示。2种优化方法得到的最优翼型及对应压力分布如图 13所示。对RAE2822翼型及最优翼型进行不确定性分析,得到阻力目标、力矩与面积约束区间上下界对应的翼型及压力分布,如图 14所示。
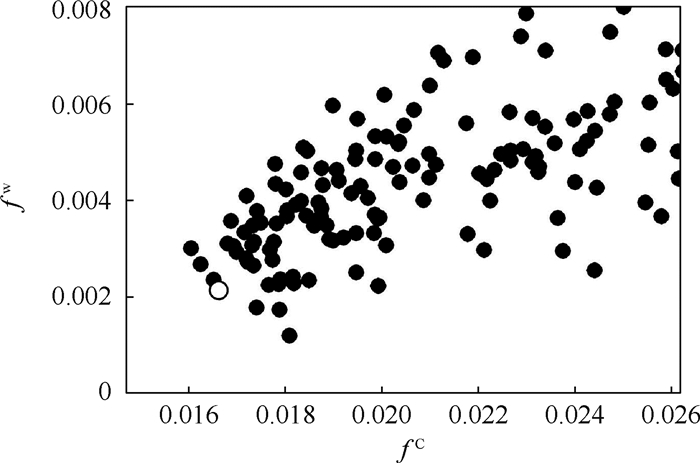
表 5 优化结果比较Table 5. Optimization result comparison翼型 CD fC fw CL CM Aa RAE2822翼型 0.021127 0.033261 0.015527 0.824888 -0.102279 0.077873 确定性优化最优翼型 0.013546 0.024063 0.010529 0.824487 -0.091623 0.078044 鲁棒优化最优翼型 0.015634 0.016627 0.002096 0.823707 -0.083295 0.082126 首先从优化翼型的CFD计算结果可看出,无论是确定性优化还是鲁棒优化最优翼型的阻力系数较初始RAE2822翼型均有较大程度的下降。从翼型几何和对应压力分布情况来看,优化使得翼型上表面前缘下降后缘抬升,造成前缘吸力峰值更高,但减弱了激波强度,从而减小阻力。确定性优化结果较鲁棒优化结果激波更平缓,阻力更小。从考虑阻力及其他约束的综合不确定性分析的结果来看,原始RAE2822翼型以及确定性优化的区间半径目标fw较鲁棒优化结果差距很大,但从表 5也可看出, 区间中值目标fC与CFD计算结果CD相差较大,说明不确定分析结果fw和fC较大主要是由约束函数造成的。
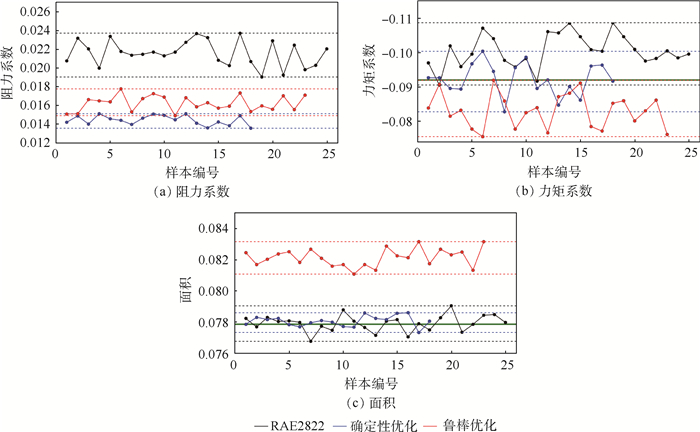
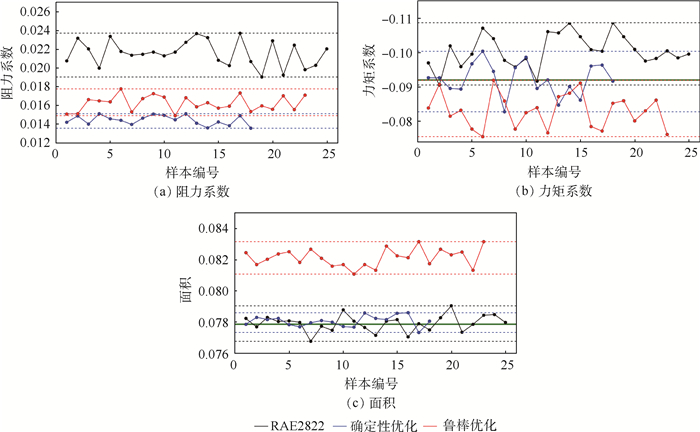
图 15为不确定分析时各采样样本的目标函数和约束函数值比较,该结果一定程度上可显示优化目标和各约束对不确定分析结果的影响。其中阻力系数结果显示,确定性优化结果的整体阻力系数较低且变化区间较小,但从力矩和面积约束的结果可看出,确定性优化的结果均在一定程度上违反了约束,而鲁棒优化结果则基本满足约束。这是因为确定性优化时,由于目标和约束的冲突,所得最优结果一般分布在约束边缘,当考虑不确定性因素时,极易违反约束。由此可见,本文鲁棒优化流程考虑了不确定性对优化目标及约束的影响,相对确定性优化,得到了综合鲁棒性更强的结果。实际操作中,也可以根据决策者对各优化目标和约束的偏好,灵活设定约束罚函数因子,得到更理想的结果。
3. 结论
1) 对NACA0012翼型的阻力系数性能进行了跨声速条件下考虑几何不确定性的快速非线性区间分析。通过建模方法与直接分析方法对比,最大误差在5%以内,而分析效率可提高95%。
2) 以跨声速条件下RAE2822翼型的阻力性能为目标,并考虑升力、力矩及面积约束,分别进行了翼型的确定性优化设计及鲁棒气动优化设计。确定性优化所得最优翼型较初始翼型阻力减小35.9%,且严格满足各项约束,同等精度下优于其他文献结果。鲁棒优化所得最优翼型较初始翼型和确定优化最优翼型,其鲁棒性得到了大幅提高。分析总体优化目标各项可知,本次优化结果主要通过降低违反约束的概率提高鲁棒性,通过调节阻力目标与其他约束的罚函数因子,可得到偏好不同的结果。
-
表 1 直接操作点x方向位置
Table 1. Position of pilot points in x direction
序号 x/c 1 0 2 0.077 3 0.214 4 0.377 5 0.571 6 0.777 7 1.0 表 2 3种方法的分析结果、误差、CFD计算次数、计算时间比较
Table 2. Comparison of analysis results, errors, CFD calculation times and computing time among three methods
方法 最大阻力系数 最大阻力系数相对误差/% 最小阻力系数 最小阻力系数相对误差/% CFD计算次数 并行计算时间/min 直接优化 0.0651303 0.0452392 800 500 Kriging模型1 0.0620658 -4.70 0.0433786 -4.10 20 25 Kriging模型2 0.06480712 -0.49 0.0457063 1.03 27 200 表 3 RAE2822翼型及优化翼型的计算结果
Table 3. Computing results of RAE2822 and optimized airfoils
翼型 CD α/ (°) CL CM Aa RAE2822 0.02112 2.75377 0.82489 -0.1023 0.07787 优化翼型 0.01354 2.84263 0.82449 -0.0916 0.07804 表 4 优化翼型与其他文献结果对比
Table 4. Comparison of optimization results between optimized airfoil and other works
表 5 优化结果比较
Table 5. Optimization result comparison
翼型 CD fC fw CL CM Aa RAE2822翼型 0.021127 0.033261 0.015527 0.824888 -0.102279 0.077873 确定性优化最优翼型 0.013546 0.024063 0.010529 0.824487 -0.091623 0.078044 鲁棒优化最优翼型 0.015634 0.016627 0.002096 0.823707 -0.083295 0.082126 -
[1] 宋述芳, 吕震宙, 张伟伟, 等.机翼气动弹性的随机不确定性分析研究[J].振动工程学报, 2009, 22(3):228-231.SONG S F, LV Z Z, ZHANG W W, et al.Random uncertainty of aeroelastic system[J].Journal of Vibration Engineering, 2009, 22(3):228-231(in Chinese). [2] 李焦赞, 高正红.气动设计问题中确定性优化与稳健优化的对比研究[J].航空计算技术, 2010, 40(2):28-31. doi: 10.3969/j.issn.1671-654X.2010.02.008LI J Z, GAO Z H.Comparison computation of deterministic optimization and robust optimization in aerodynamic design[J].Aeronautical Computing Technique, 2010, 40(2):28-31(in Chinese). doi: 10.3969/j.issn.1671-654X.2010.02.008 [3] BAE H R, GRANDHI R, CANFIELD R.Reliability-based design optimization under imprecise uncertainty: AIAA-2005-2069[R].Reston: AIAA, 2005. [4] 徐明, 李建波, 彭名华, 等.基于不确定性的旋翼转速优化直升机参数设计[J].航空学报, 2016, 37(7):2170-2179.XU M, LI J B, PENG M H, et al.Parameter design of helicopter with optimum speed rotor based on uncertainty optimization[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(7):2170-2179(in Chinese). [5] SALEHI S, RAISEE M, CERVANTES M J, et al.On the flow field and performance of a centrifugal pump under operational and geometrical uncertainties[J].Applied Mathematical Modelling, 2018, 61:540-560. doi: 10.1016/j.apm.2018.05.008 [6] 邬晓敬, 张伟伟, 宋述芳, 等.翼型跨声速气动特性的不确定性及全局灵敏度分析[J].力学学报, 2015, 47(4):587-595.WU X J, ZHANG W W, SONG S F, et al.Uncertainty quantification and global sensitivity analysis of transonic aerodynamics about airfoil[J].Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(4):587-595(in Chinese). [7] 戴玉婷, 杨超.考虑随机型不确定性的浸入式颤振求解方法[J].航空学报, 2014, 35(8):2182-2189.DAI Y T, YANG C.Intrusive flutter solutions with stochastic uncertainty[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(8):2182-2189(in Chinese). [8] PAPADIMITRIOU D I, PAPADIMITRIOU C.Aerodynamic shape optimization for minimum robust drag and lift reliability constraint[J].Aerospace Science and Technology, 2016, 55:24-33. doi: 10.1016/j.ast.2016.05.005 [9] ELISHAKOFF I. Discussion on:A non-probabilistic concept of reliability[J].Structural Safety, 1995, 17(3):195-199. doi: 10.1016/0167-4730(95)00010-2 [10] 屈小章, 刘桂萍, 韩旭, 等.基于区间的风机系统翼型气动性能不确定性优化[J].中国科学:技术科学, 2017, 47(9):955-964.QU X Z, LIU G P, HAN X, et al.Uncertain optimum design of aerodynamic performance of fan with interval uncertainty[J].SCIENTIA SINICA Technologica, 2017, 47(9):955-964(in Chinese). [11] ZHENG Y N, QIU Z P.Uncertainty propagation in aerodynamic forces and heating analysis for hypersonic vehicles with uncertain-but-bounded geometric parameters[J].Aerospace Science and Technology, 2018, 77:11-24 doi: 10.1016/j.ast.2018.02.028 [12] 张军红, 韩景龙.含区间不确定性参数的机翼气动弹性优化[J].振动工程学报, 2011, 24(5):461-467. doi: 10.3969/j.issn.1004-4523.2011.05.002ZHANG J H, HAN J L.Aeroelasticity optimization of wing including interval uncertainty parameters[J].Journal of Vibration Engineering, 2011, 24(5):461-467(in Chinese). doi: 10.3969/j.issn.1004-4523.2011.05.002 [13] PISARONI M, LEYLAND P, NOBILE F.A multi level Monte Carlo algorithm for the treatment of geometrical and operational uncertainties in internal and external aerodynamics: AIAA-2016-4398[R].Reston: AIAA, 2016. [14] 张德虎, 席胜, 田鼎.典型翼型参数化方法的翼型外形控制能力评估[J].航空工程进展, 2014, 5(3):281-295. doi: 10.3969/j.issn.1674-8190.2014.03.003ZHANG D H, XI S, TIAN D.Geometry control ability evaluation of classical airfoil parametric methods[J].Advances in Aeronautical Science and Engineering, 2014, 5(3):281-295(in Chinese). doi: 10.3969/j.issn.1674-8190.2014.03.003 [15] 陈颂, 白俊强, 孙智伟, 等.基于DFFD技术的翼型气动优化设计[J].航空学报, 2014, 35(3):695-705.CHEN S, BAI J Q, SUN Z W, et al.Aerodynamic optimization design of airfoil using DFFD technique[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3):695-705(in Chinese). [16] 姜潮, 韩旭, 谢慧超.区间不确定性优化设计理论与方法[M].北京:科学出版社, 2017:6-40.JIANG C, HAN X, XIE H C.Interval uncertain optimization design:theory and methods[M].Beijing:Science Press, 2017:6-40(in Chinese). [17] 韩忠华.Kriging模型及代理优化算法研究进展[J].航空学报, 2016, 37(11):3197-3225.HAN Z H.Kriging surrogate model and its application to design optimization:A review of recent progress[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(11):3197-3225(in Chinese). [18] 郑冠男, 邓守春, 韩同来, 等.基于混合网格Navier-Stokes方程的并行隐式计算方法研究[J].应用力学学报, 2011, 28(3):211-218.ZHENG G N, DENG S C, HAN T L, et al.An implicit parallel computing method based on the Navier-Stokes equations with hybrid grids[J].Chinese Journal of Applied Mechanics, 2011, 28(3):211-218(in Chinese). [19] AMOIGNON O, HRADIL J, NAVRATIL J.Study of parameterizations in the project CEDESA: AIAA-2014-0570[R].Reston: AIAA, 2014. [20] ANDERSON G R, NEMEC M, AFTOSMIS M J.Aerodynamic shape optimization benchmarks with error control and automatic parameterization: AIAA-2015-1719[R].Reston: AIAA, 2015. [21] POOLE D J, ALLEN C B, RENDALL T.Control point-based aerodynamic shape optimization applied to AIAA ADODG test cases: AIAA-2015-1947[R].Reston: AIAA, 2015. [22] 胡旺, YEN G G, 张鑫.基于Pareto熵的多目标粒子群优化算法[J].软件学报, 2014, 25(5):1025-1050.HU W, YEN G G, ZHANG X.Multiobjective particle swarm optimization based on pareto entropy[J].Journal of Software, 2014, 25(5):1025-1050(in Chinese). 期刊类型引用(3)
1. 董欣心,刘莉,葛佳昊,王志. 捆绑火箭气动载荷分布不确定性分析. 北京航空航天大学学报. 2022(03): 464-472 .  本站查看
本站查看2. 张威,王强,路嘉晨,阎超. 基于PCA-HicksHenne方法的几何不确定性稳健优化设计. 北京航空航天大学学报. 2022(12): 2473-2481 .  本站查看
本站查看3. 王媛. 基于Pareto最优解的两轮农耕机机构优化设计. 自动化与仪器仪表. 2020(08): 128-131 .  百度学术
百度学术其他类型引用(6)
-








 下载:
下载:















 下载:
下载:









 百度学术
百度学术