-
摘要:
发动机短舱泄压门的设计会影响到短舱的安全性,泄压是一个动态变化过程,与舱内外压力、外界气流马赫数及泄压门结构有关。基于Modelica语言建立了短舱泄压过程零维瞬态仿真数学模型,并通过计算流体力学(CFD)方法得到不同开启角度下所需泄压门排放质量流量和力矩系数,并将这些系数代入零维瞬态仿真数学模型,得到了短舱泄压过程中舱内压力、泄压门开启角度等关键参数随时间的变化关系,分析了泄压门开启舱内压力阈值及最大开启角度对泄压过程的影响。研究结果显示,降低泄压门开启舱内压力阈值会使泄压过程到达平衡阶段时间减小,但是对平衡阶段舱内压力和往复摆动角度/幅度无影响。适当降低最大开启角度可有效降低泄压平衡阶段往复摆动角度/幅度,而对初始阶段的泄压速率和平衡阶段的短舱内部压力基本无影响,但是随着最大开启角度进一步降低,则会导致泄压速率下降,并使平衡阶段短舱内部压力升高。
-
关键词:
- 发动机短舱 /
- 泄压过程 /
- 瞬态模型 /
- 泄压门 /
- 计算流体力学(CFD)
Abstract:The design of the engine nacelle pressure relief door will affect the safety of the nacelle. The pressure relief is a dynamic process, which is related to the pressure inside and outside the nacelle, the freestream Mach number and the structure of the pressure relief door. Based on the Modelica language, a zero-dimensional transient simulation mathematical model of the nacelle pressure relief process was established, and the pressure relief door (PRD) discharge and moment coefficient under different opening angles were calculated via computational fluid dynamics (CFD). Then those coefficients were substituted into the zero-dimensional transient simulation model, and the variation relationship of key parameters such as the plenum compartment pressure and opening angle of the PRD with time during the pressure relief process is obtained. The influence of the plenum compartment pressure threshold and the maximum opening angle of the PRD on the pressure relief process was analyzed. The study results show that reducing the plenum compartment pressure threshold for PRD opening will reduce the time required for the pressure relief process reaching to the equilibrium stage, but has no effect on the plenum compartment pressure and reciprocating swing angle/amplitude at equilibrium stage; properly reducing the maximum opening angle can effectively reduce the PRD reciprocating swing angle/amplitude in the equilibrium stage, and has no effect on the pressure relief rate in the initial stage and the plenum compartment pressure in the equilibrium stage, but excessive reduction of the maximum opening angle will decrease the pressure relief rate in the initial stage and increase plenum compartment pressure in the equilibrium stage.
-
中国民用航空规章第25部《运输类飞机适航标准》CCAR25.1103(d)条款规定[1]:对于涡轮发动机和辅助动力装置的引气导管系统,如在空气导管引气口与飞机用气装置之间任意部位上的导管破损,不得造成危害。发动机引气管道发生破裂或泄漏时,迅速上升的短舱内部压力可能会破坏短舱结构甚至损坏发动机,因此需安装泄压门(Pressure Relief Door,PRD)保证压力升高到一定阈值后,通过开启泄压门泄压避免短舱结构损坏或发动机故障。
短舱泄压过程是一个复杂的流动行为,不仅与短舱内外界压力、外流马赫数有关,还受到泄压门开启方式和角度及纵横比的影响。早在1957年,Vick[2]就进行了辅助排气口经过曲面管道且出口有一挡板时排气到跨声速气流中的排放和受力特性试验,试验选择了一系列压力比和马赫数,研究了挡板开启角度和纵横比对性能的影响,为泄压门设计提供了基础试验数据。
Pratt等[3-4]为了分析挡板对流场结构的影响,使用Vick[2]报告中的试验装置作为计算域进行了CFD计算,结果与试验数据基本吻合。随后,Benard等[5]对压力比大于1的泄压门排放特性进行了试验研究,结果表明在给定压力比下,排放系数随马赫数的增加而减小。Vedeshkin等[6]研究了一种与前述不同的开启方式,即泄压门铰链与来流方向平行,CFD计算和试验之间存在很好的一致性。Schott[7]考虑了泄压门纵横比、倒圆角、铰链类型、侧壁边缘围护等因素的影响,在一系列压力比、马赫数、内部温度、外界高度等条件下对短舱核心舱泄压门的排放性能和受力进行了CFD计算,得到许多对泄压门设计具有指导作用的结论。
但是上述研究中泄压门均处于静止状态,并不能反映实际泄压过程中舱内压力和开启角度随时间的瞬态变化关系。
郁成德[8]对飞机增压舱突然泄压情况进行了计算,得到了增压舱突然泄压情况下各隔舱压力载荷变化。刘华源和屠毅[9]利用Simulink仿真软件建立了民机增压舱一维动态仿真模型,对泄压过程中各增压舱瞬间压力分布进行了仿真,得到了舱室体积和舱间流通面积等参数对泄压载荷的影响。但是这些研究中,仅考虑了固定泄压口对舱内压力的影响,且没有飞机外部气流对泄压过程的作用,因此相较于发动机短舱泄压过程简单。
目前国内外均没有有关于短舱泄压门瞬态泄压过程的研究的公开报道,而庞巴迪公司与中国航发商用航空发动机有限责任公司合作过程中,对泄压门的参数选择也仅给出结果,而不提供详细的设计过程,因此掌握不同操作参数和结构参数对瞬态泄压过程的影响十分重要。采用试验方法研究成本昂贵、周期长,通过仿真计算可以减少研究代价和缩短研究周期。最精确的仿真方法是基于CFD方法,考虑气体的流动和泄压门固体受力和变形,采用流固耦合来描述泄压过程,但是该方法计算代价巨大,不利于工程设计中快速评估参数的合理性。另外一种方法是基于集中参数法的零维模型,例如文献[8-9]中采用该方法,但是该模型中很难精确计算不同马赫数的外流和不同压力的内流对泄压门的作用。
本文提出一种新的计算方法,首先采用稳态CFD方法,在某个固定的开启角度,得到不同马赫数、舱内压力、纵横比等参数下的流量系数CD和力矩M,改变开启角度,获取泄压门的流量特性关系与开启角度的关系;然后建立短舱泄压零维瞬态仿真数学模型,采用将得到的CD和M代入该模型进行计算。该方法在保证计算精度的同时大大降低了计算代价,从而更好地满足实际工程需要。
Modelica语言是为解决多领域物理系统的统一建模与协同仿真,在归纳和统一先前多种建模语言的基础上,于1997年提出的一种基于方程的陈述式、面向对象的、非因果建模语言[10-11]。Modelica语言采用数学方程描述不同领域子系统的物理规律和现象,根据物理系统的拓扑结构基于语言内在的组件连接机制实现模型构成和多领域集成,通过求解微分代数方程系统实现仿真运行。Modelica语言已广泛应用于各个学科,如航空航天、电力系统、汽车系统、燃料电池等领域[12-17]。因此,本文采用Modelica语言建立仿真模型,并对模型进行求解。
1. 短舱泄压过程零维瞬态仿真数学模型
1.1 泄压过程简化和基本假设
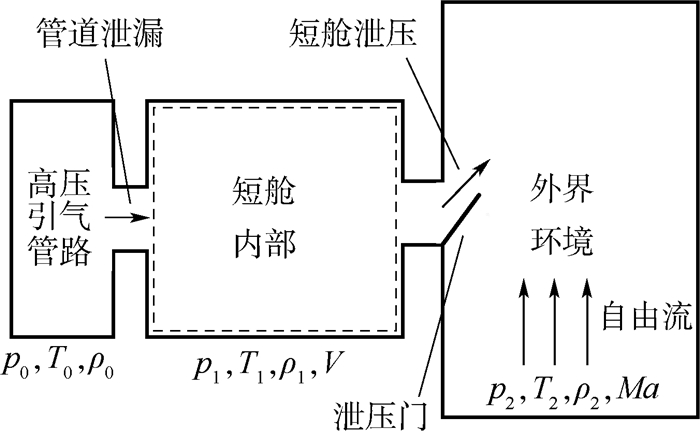
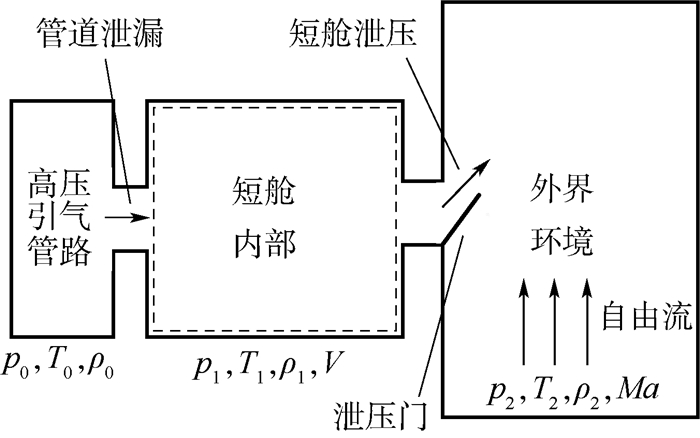
高压引气管路破裂后产生泄漏,泄漏的气体流入短舱内部,导致短舱内压力升高直至高于阈值后泄压门开启,泄压门受到短舱内外压力、泄压门开启方式、纵横比及开启角度等因素的影响,因而是一个多因素耦合作用的复杂流动过程,将泄压过程进行简化,如图 1所示。为简化计算的难度,忽略一些不重要的因素,作如下假设:高压引气管路及短舱外界环境压力、温度在整个泄压过程内保持不变;空气均视为理想气体,且泄压时不考虑传热作用,视为绝热过程;认为在短舱内部控制容积内的热力参数如温度、压力、密度等均匀一致;短舱泄压过程内部气体排放均通过泄压门排放,即不存在其他气体泄漏;泄压门刚性足够强,不考虑其变形对泄压过程的影响。
1.2 零维瞬态仿真数学模型
临界压比为

(1) 式中:γ为理想气体的定熵绝热指数。
当p1/p0≥πp, cr时,流动为非临界状态,此时高压引气管路泄漏质量流量为

(2) 式中:μ为高压引气管路泄漏流量系数[18];A为泄漏面积;R为空气的气体常数;p0为高压引气管路压力;T0为高压引气管路温度;p1为短舱内部压力。
当p1/p0 < πp, cr时,流动为临界状态,此时高压引气管路泄漏质量流量为

(3) 当p2/p1≥πp, cr时,流动为非临界状态,此时泄压门排放质量流量为

(4) 当p2/p1 < πp, cr时,流动为临界状态,此时泄压门排放质量流量为

(5) 式中:CD为泄压门在不同舱内压力及开启角度下的流量系数,其根据CFD稳态仿真计算得到;Adoor为泄压门面积;φ为泄压门开启角度;T1为短舱内部温度;p2为外界环境自由流静压。
短舱内部空间质量随时间变化为

(6) 式中:m1为短舱内部气体质量;m1, in为舱内流入气体质量;m1, out为舱内流出气体质量。
联立绝热流动过程方程p/ργ=C(C为常数)与理想气体状态方程pV=mRT并对时间求导可得

(7) 短舱内部温度随时间变化为

(8) 泄压门转动时,泄压门转动角加速度α为

(9) 式中:ω为转动角速度;M为排放的高压气体与外流气体作用在泄压门表面产生的力矩,其根据CFD稳态仿真计算得到;J为泄压门绕铰链转动的转动惯量[19];Mf为泄压门转动时的阻力矩,即

(10) 其中:c为泄压门转动阻力系数;ρ为排放气体密度;l为泄压门弦长;b为泄压门宽度。
2. CFD稳态仿真计算
2.1 几何模型及网格生成
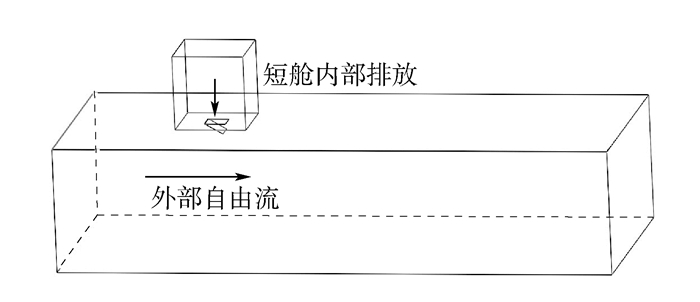
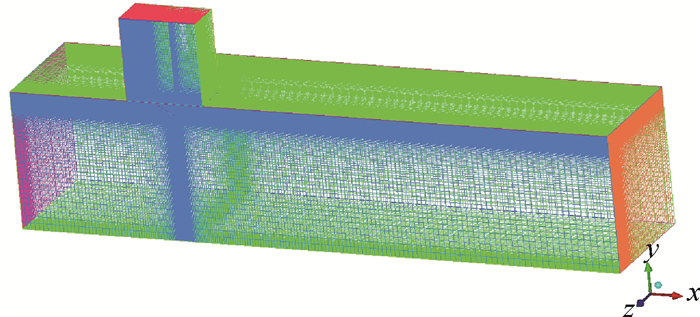
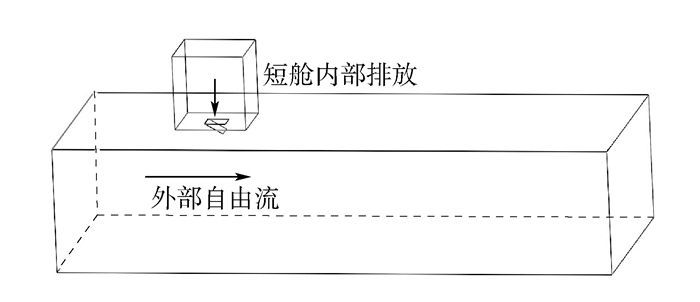
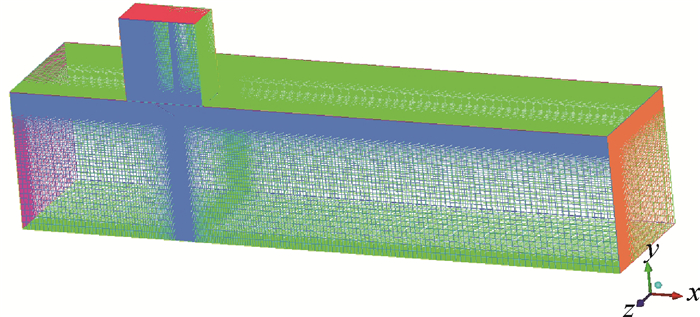
飞机发动机短舱泄压门实际应用的结构示意如图 2所示。本文考虑实际泄压门的结构及尺寸,并分析计算域大小对泄压门出口流动结构的影响,采用图 3所示几何结构模型进行CFD稳态仿真计算。该模型上部是一个尺寸为85cm×85cm×95cm的高压室,以模拟短舱内部引气管道泄漏后的高压区域,下部280cm×150cm×665cm矩形自由流动区域模拟飞行时短舱外界高速气流,且上下部之间存在3mm间距来模拟短舱和泄压门壁厚,泄压门纵横比为1,尺寸为25cm×25cm的矩形,其中泄压门开启方式为泄压门铰链与来流方向垂直。考虑到泄压门表面边界层需要加密及泄压门出口附近流动的复杂结构,使用ICEM CFD划分得到高质量的结构化网格,如图 4所示。由于结构对称,因此计算使用对称模型,其在满足要求的情况下大大减少计算量,模型网格数量约为460万。
2.2 计算条件及边界条件
在外界自由流马赫数为0.7,短舱内部压力分别为0.10、0.12、0.14和0.16MPa下,对泄压门开启角度分别为10°、20°、30°、40°和50°时进行计算。由于Realizable k-ε湍流双方程模型处理强流线弯曲流动,尤其对旋转均匀剪切流、边界层流、二次流的模拟更加精确,因此本文计算选用Realizable k-ε湍流双方程模型进行计算及与试验数据对比验证。
下部自由流动区域设为压力进口和压力出口,自由流入口总压设为101.3kPa,通过改变自由流静压调节来流马赫数,来流入口总温为300K,上部高压室入口为压力入口。
2.3 CFD计算验证
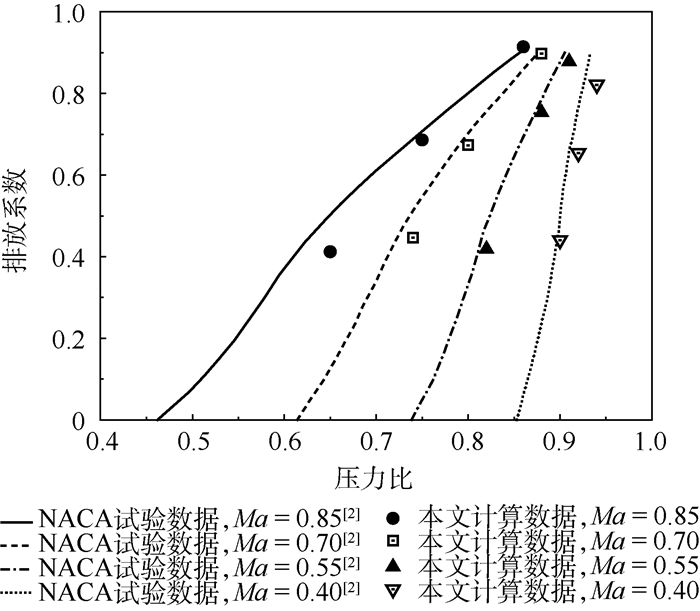
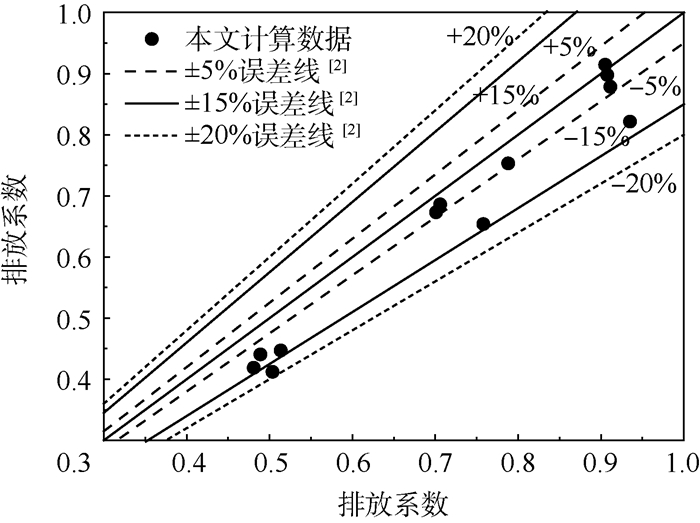
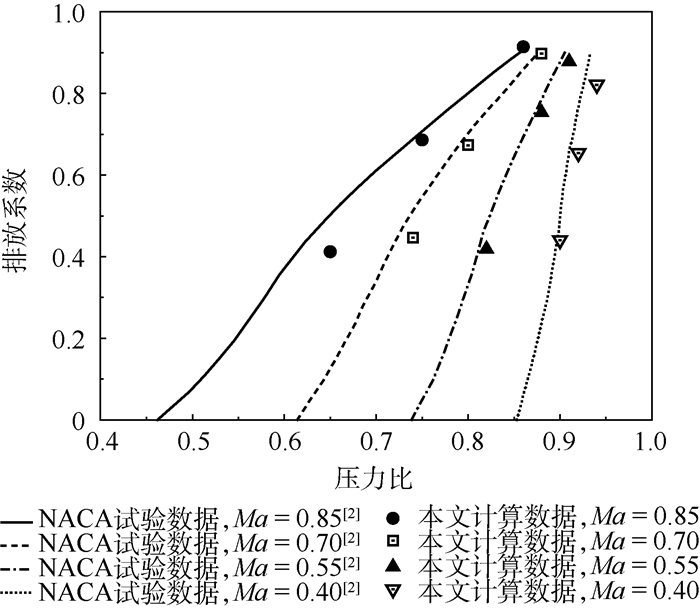
为验证CFD计算的正确性,采用上述建模方法及计算方法对NACA TN4007报告的试验装置进行建模计算[2]。将计算结果与NACA TN4007报告中的试验数据进行对比,结果如图 5所示,误差分析如图 6所示。结果显示本文计算结果半
数误差低于5%,最大误差不超过20%,这表明所建立模型和计算方法的正确性。
压力比为

(11) 式中:pe为短舱内部总压;p∞为短舱外部自由流总压。
排放系数为

(12) 式中:

2.4 CFD稳态仿真计算结果
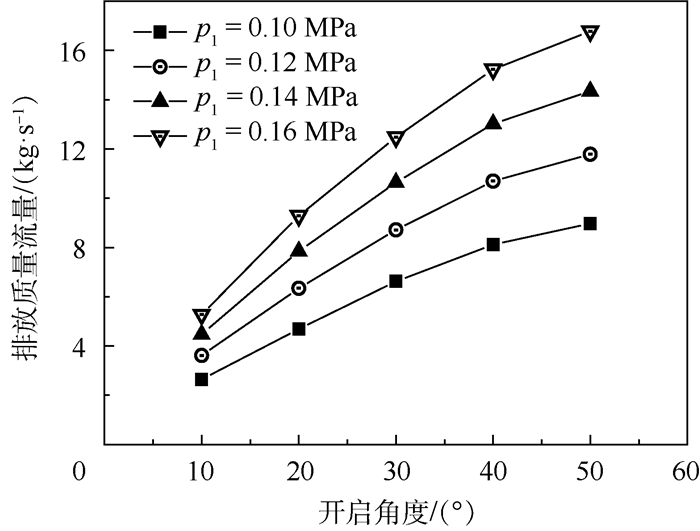
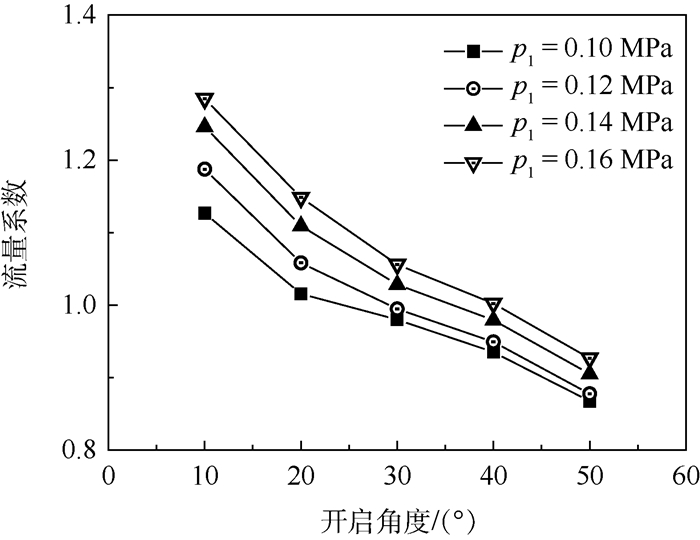
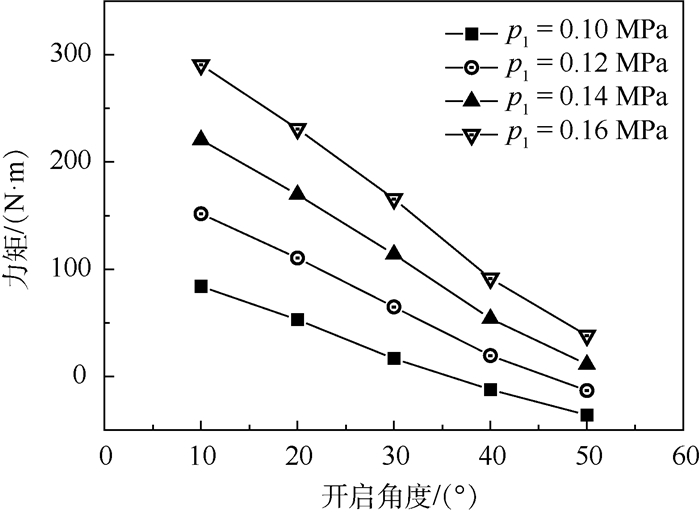
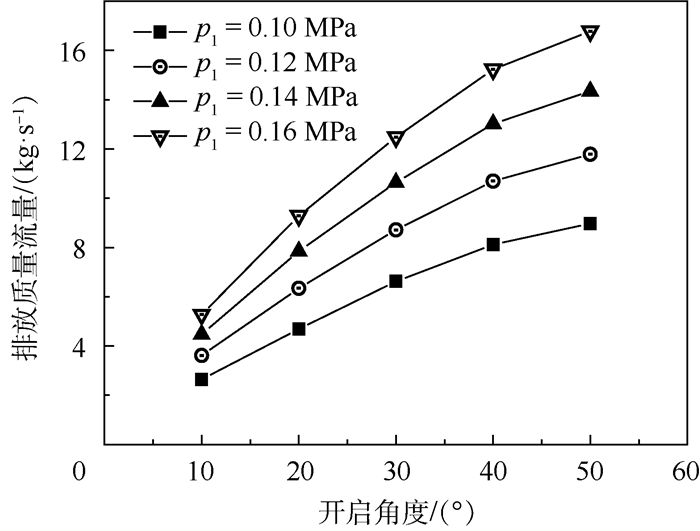
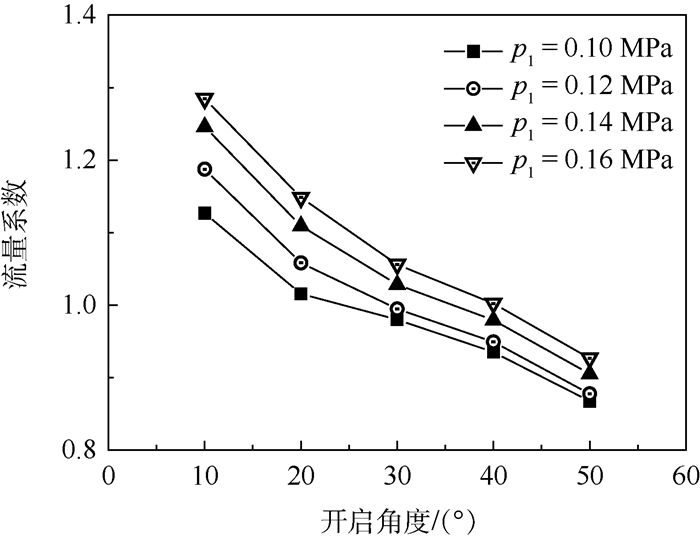
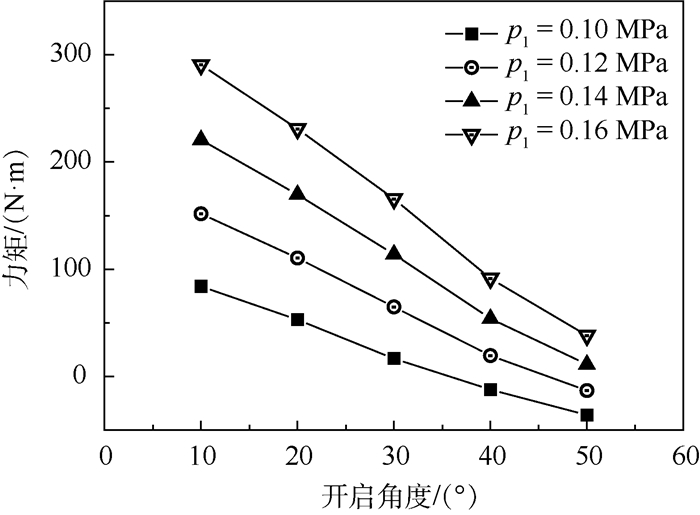
泄压门排放质量流量、流量系数CD与所受力矩M随泄压门开启角度和舱内压力变化的计算结果分别如图 7~图 9所示(马赫数为0.7)。
3. 短舱泄压过程瞬态计算结果
计算和分析中认为马赫数为0.7,高压引气管路压力为0.4MPa,舱内压力为0.10MPa,泄压门面积为0.0625m2,纵横比为1,泄压门开启方式为泄压门铰链与来流方向垂直。
3.1 泄压门开启阈值对泄压过程的影响
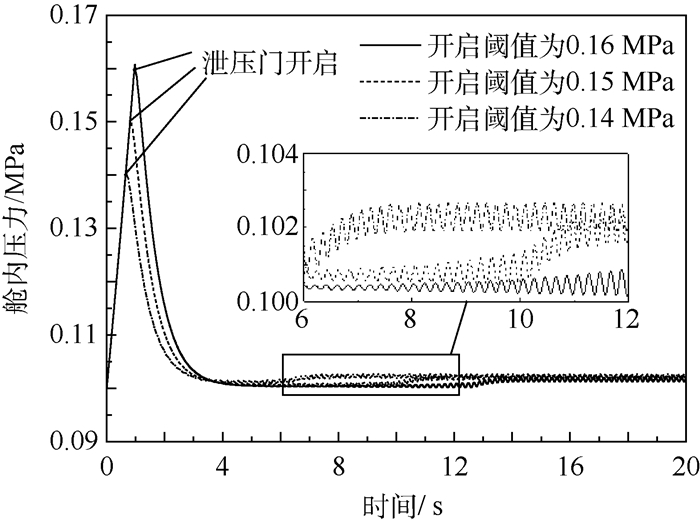
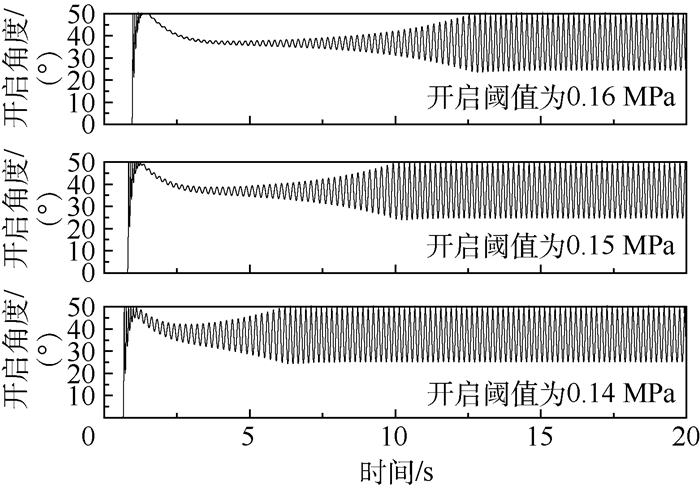
将泄压门最大开启角度定为50°,对泄压门开启舱内压力阈值分别为0.16、0.15、0.14MPa进行计算,得到舱内压力及泄压门开启角度随时间变化分别如图 10和图 11所示。
由图 10和图 11可知,初始舱内压力为0.10MPa,当高压引气管路发生大面积泄漏后,短舱内部压力迅速上升,当舱内压力达到阈值0.14、0.15、0.16MPa时,泄压门开启,随后在3.8s时刻左右,舱内压力降至0.1MPa左右,期间由于舱内压力降低,泄压门力矩平衡角不断减小,即泄压门开启角度降低,同时高压舱内通过泄压门排放的气体质量流量减小,导致舱内压力有所升高,泄压门力矩平衡角也升高,泄压门排放质量流量增加,舱内压力再次降低。因此泄压门在舱内压力和外部自由流的作用下,发生往复摆动直至达到平衡状态,到达平衡阶段后,由于泄压门在往复摆动下排放的气体质量流量低于稳定在平衡角时的质量流量,因此舱内压力有所回升,最终稳定在0.102MPa左右。
对不同开启阈值下舱内压力及泄压门开启角度随时间变化计算结果分析可知,泄压门开启阈值的改变主要影响泄压门初始阶段,随着开启阈值的降低,泄压门到达平衡阶段所需时间减小,但开启阈值的改变不影响平衡阶段的舱内压力和往复摆动角度。
3.2 泄压门最大开启角度对泄压过程的影响
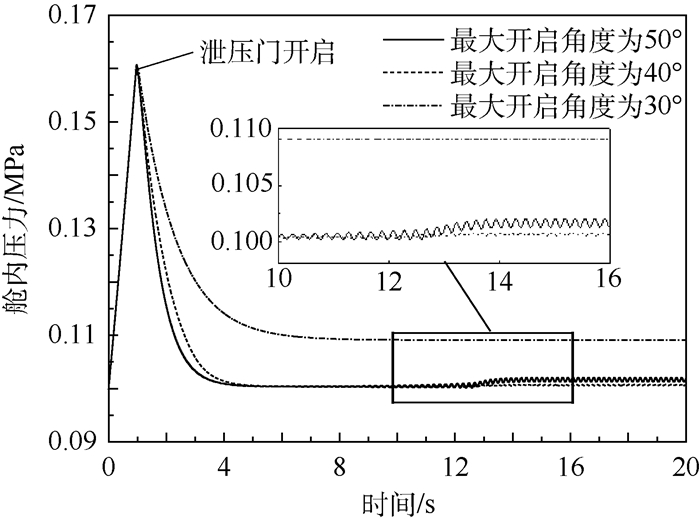
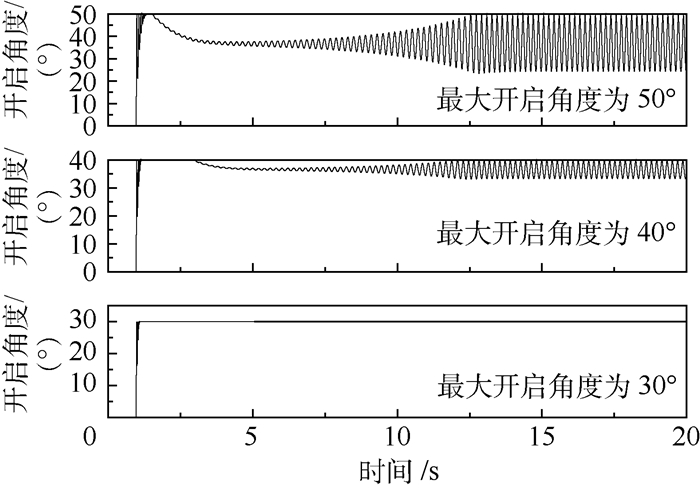
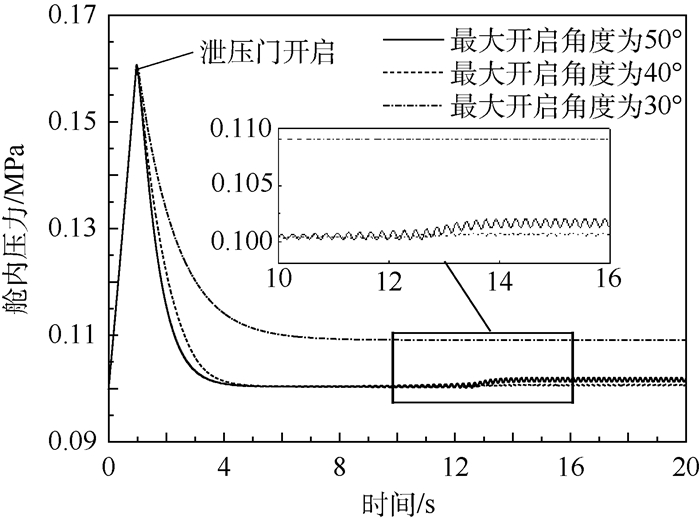
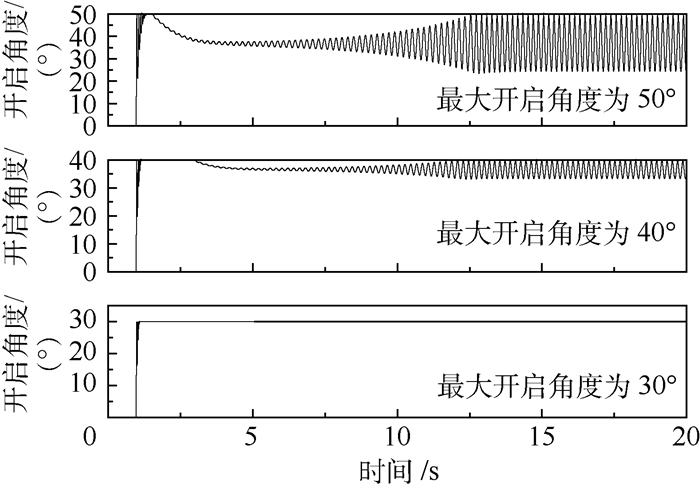
将泄压门开启舱内阈值定为0.16MPa,对泄压门最大开启角度分别为30°、40°和50°这3种情况进行计算,得到舱内压力及泄压门开启角度随时间变化如图 12和图 13所示。
根据图 12和图 13所示计算结果可知,适当降低泄压门最大开启角度,如由50°降低至0°,可有效减小泄压门往复摆动角度,而对泄压门初始阶段舱内压力下降速率及平衡阶段舱内压力基本无影响,平衡阶段舱内压力稳定在0.102MPa左右;但过多的降低最大开启角度,如降低至30°,由于该角度小于泄压门力矩平衡角,因此泄压门在高压室排放气体及外界气流作用下保持在最大开启角度即30°,在该最大开启角度下,初始阶段舱内压力下降速率降低,且平衡阶段舱内压力升高至0.109MPa。
4. 结论
建立了短舱泄压过程零维瞬态仿真数学模型,并通过CFD稳态仿真计算得到零维瞬态仿真数学模型所需流量系数CD和力矩M。对泄压门开启舱内压力阈值、最大开启角度对短舱泄压过程的影响进行仿真计算,研究显示:
1) 所建立的零维瞬态仿真数学模型可有效分析泄压时舱内压力及泄压门开启角度随时间变化关系,高压引气管路泄漏会使短舱内部压力迅速升高,而泄压门泄压过程可降低舱内压力从而避免破坏短舱结构。
2) 泄压初始阶段,舱内压力较高,此时泄压门力矩平衡角很大,因此泄压门达到最大开启角度;而随着泄压过程的进行,舱内压力逐渐降低并趋于某一值附近,当泄压门力矩平衡角低于最大开启角度时,泄压门会在平衡角附近往复摆动,舱内压力也会出现微小波动。
3) 降低泄压门开启舱内压力阈值,会影响泄压初始阶段舱内压力变化,使泄压过程到达平衡状态所需时间减小,但对平衡阶段基本无影响。
4) 适当降低泄压门最大开启角度,可有效减小泄压门平衡阶段往复摆动角度,且对泄压初始阶段泄压速率及平衡阶段舱内压力影响很小;而过多地降低最大开启角度导致最大开启角度低于泄压平衡角时,会大大降低泄压速率,且会提高平衡阶段舱内压力。
-
-
[1] 中国民用航空局.中国民用航空规章第25部运输类飞机适航标准: CCAR-25-R3[S].北京: 中国民用航空局, 2001.Civil Aviation Administration of China.Chinese civil aviation regulations Part 25 airworthiness standards for transport category aircraft: CCAR-25-R3[S]. Beijing: Civil Aviation Administration of China, 2001(in Chinese). [2] VICK A R. An investigation of discharge and thrust characteristics of flapped outlets for stream Mach numbers from 0.40 to 1.30: NACA TN4007[R]. Washington, D.C.: NACA, 1957. [3] PRATT P R, WATTERSON J K, BENARD E.Computational and experimental studies of pressure relief doors in ventilated nacelle compartments[J]. Investigative Ophthalmology & Visual Science, 2003, 28(10):1678-1686. [4] PRATT P R, WATTERSON J K, BENARD E, et al.Performance of a flapped duct exhausting into a compressible external flow[C]//CD-ROM Proceedings of 24th International Congress of the Aeronautical Sciences.Yokohama: Optimage Ltd., 2004, 1: 1-9. [5] BENARD E, WATTERSON J K, GAULT R, et al.Review and experimental survey of flapped exhaust performance[J]. Journal of Aircraft, 2008, 45(1):349-352. doi: 10.2514/1.34238 [6] VEDESHKIN G, DUBOVITSKIY A, BONDARENKO D, et al.Experimental investigations of hydraulic devices performance in aviation engine compartment[C]//28th Congress of the International Council of the Aeronautical Sciences 2012.Brisbane: Curran Associates, Inc., 2013, 2: 1692-1700. [7] SCHOTT T. Computational analysis of aircraft pressure relief doors[D]. Colorado: Colorado State University, 2016. [8] 郁成德.增压舱突然泄压载荷计算[J].民用飞机设计与研究, 1997(2):43-49.YU C D.Calculation of pressurized cabin pressure relief load[J]. Civil Aircraft Design & Research, 1997(2):43-49(in Chinese). [9] 刘华源, 屠毅.民用飞机泄压载荷影响因素研究[J].科技视界, 2016(16):30-31. doi: 10.3969/j.issn.2095-2457.2016.16.016LIU H Y, TU Y.Numerical simulation of decompression in pressurized cabin of civil aircraft[J]. Science & Technology Vision, 2016(16):30-31(in Chinese). doi: 10.3969/j.issn.2095-2457.2016.16.016 [10] 赵建军, 丁建完, 周凡利, 等.Modelica语言及其多领域统一建模与仿真机理[J].系统仿真学报, 2006, 18(2):570-573.ZHAO J J, DING J W, ZHOU F L, et al.Modelica and its mechanism of multi-domain unified modeling and simulation[J]. Journal of System Simulation, 2006, 18(2):570-573(in Chinese). [11] TILLER M. Introduction to physical modeling with Modelica[M]. Boston: Kluwer Academic, 2001. [12] LOVERA M, PULECCHI T.Object-oriented modelling for spacecraft dynamics: A case study[C]//Proceedings of the 2006 IEEE Conference on Computer Aided Control Systems Design.Piscataway, NJ: IEEE Press, 2006: 1898-1903. [13] CASELLA F, LOVERA M.High-accuracy orbital dynamics simulation through keplerian and equinoctial parameters[C]//Proceedings of the 6th International Modelica Conference.Bielefeld: The Modelica Association, 2008, 2: 505-514. [14] 张宝坤, 赵建军, 刘伟.关于飞机液压负载功率系统优化设计研究[J].计算机仿真, 2017, 34(5):82-87. doi: 10.3969/j.issn.1006-9348.2017.05.018ZHANG B K, ZHAO J J, LIU W.Research on aircraft hydraulic load power system optimization design[J]. Computer Simulation, 2017, 34(5):82-87(in Chinese). doi: 10.3969/j.issn.1006-9348.2017.05.018 [15] 李志为, 赵洪山.基于Modelica语言的电力系统建模与仿真[J].华东电力, 2012(3):425-428.LI Z W, ZHAO H S.Modeling and simulation of power system based on Modelica[J]. East China Electric Power, 2012(3):425-428(in Chinese). [16] 程雷, 秦东晨, 王耀凯, 等.基于Modelica的纯电动客车建模仿真研究[J].汽车技术, 2017(8):43-48. doi: 10.3969/j.issn.1000-3703.2017.08.008CHENG L, QING D C, WANG Y K, et al.Modeling and simulation of pure electric bus based on Modelica[J]. Automobile Technology, 2017(8):43-48(in Chinese). doi: 10.3969/j.issn.1000-3703.2017.08.008 [17] RUBIO M, URQUIA A, GONZÁLEZ L, et al.FuelCellLib-a modelica library for modeling of fuel cells[C]//Proceedings of the 4th International Modelica Conference.Hamburg: The Modelica Association, 2005, 1: 75-83. [18] 孟亦飞, 蒋军成.化工装置泄漏扩散定量风险分析[J].石油化工高等学校学报, 2008, 21(4):50-54. doi: 10.3969/j.issn.1006-396X.2008.04.013MENG Y F, JIANG J C.Calculation of high-pressure gas tank leakage parameters[J]. Industrial Safety and Environmental Protection, 2008, 21(4):50-54(in Chinese). doi: 10.3969/j.issn.1006-396X.2008.04.013 [19] 范钦珊.理论力学[M].北京:高等教育出版社, 2000:264-265.FAN Q S.Theoretical mechanics[M]. Beijing:Higher Education Press, 2000:264-265(in Chinese). 期刊类型引用(3)
1. 季佳圆,邓阳,刘天依,何鹏,马率,肖中云. 短舱泄压门几何参数对流动特性的影响. 航空动力学报. 2024(08): 326-333 .  百度学术
百度学术2. 马率,刘钒,季佳圆,邓阳,张露. 短舱泄压门流场对排放特性影响的数值模拟. 航空动力学报. 2023(10): 2338-2348 .  百度学术
百度学术3. 王晨臣,潘俊,王洋洋. 飞机发动机短舱泄压过程研究. 航空科学技术. 2021(04): 29-34 .  百度学术
百度学术其他类型引用(1)
-








 下载:
下载:












 下载:
下载:




 百度学术
百度学术