Physical interpretation of mathematical homogenization method for thermomechanical problem
-
摘要:
针对复合材料周期结构热力耦合问题，通过构造各阶摄动项的全解耦格式，推导了高阶数学均匀化方法（MHM）的数学表达式，并使用加权残量方法将其转换为易于编程实现的矩阵列式。将弹性影响函数和热影响函数分别比拟为弹性虚拟位移和热虚拟位移，通过弹性虚拟载荷和热虚拟载荷的自平衡特性、量纲分析及几何直观等角度揭示了各阶影响函数和摄动位移的物理意义，并指出二阶摄动位移对于细观结构分析的必要性。数值计算结果验证了高阶MHM矩阵列式及物理意义分析的正确性。
-
关键词:
- 周期复合材料结构 /
- 数学均匀化方法(MHM) /
- 热力耦合 /
- 摄动位移 /
- 物理意义
Abstract:The mathematical expression of high-order mathematical homogenization method (MHM) is formulated by constructing decoupling form of each order perturbation for the thermomechanical problem of periodical composite structure, and it is converted into a matrix form by weighted residual method, which is convenient for use as standard finite element method. The elastic influence function and the heat influence function are respectively compared to the elastic virtual displacement and the thermal virtual displacement, and the physical interpretation of each order influence function and perturbation displacement are revealed by the self-balancing characteristics and dimensional analysis and geometric visualization. The second-order perturbation displacement is emphasized for the analysis of micro structure. The numerical results verify the correctness of high-order MHM matrix form and the analysis of physical interpretation.
-
复合材料具有比强度高、比刚度大等优点, 广泛应用于航天、航空工业领域。众所周知，对于很多复合材料的宏观解，如低阶频率和模态，可以使用等应变模型或等应力模型[1]及其他均匀化方法[2]求解，但相对于宏观应力分析，细观结构分析要复杂很多。为了在计算精度和效率之间达到平衡，各种多尺度方法相继被提出，如数学均匀化方法(MHM)[3-4]、广义有限单元方法(GFEM)[5-6]、多尺度有限单元方法(MsFEM)[7-8]、异类多尺度方法(HMM)[9-10]及多尺度特征单元方法(MEM)[11-12]。其中，MHM是最具代表性的多尺度方法之一，因其具有严格的数学逻辑，且可以包含复合材料所有的细观结构信息, 广泛应用于分析热力耦合作用下的周期复合材料结构响应问题[13-18]。
在应用MHM处理热力耦合作用下的复合材料结构响应问题时，摄动阶次的选择是不可回避的问题，然而多数文献只考虑了一阶摄动项，这对于细观结构物理和力学信息的捕捉往往是不够的[19]，在很多实际工程问题中[20-25]，二阶摄动项对于计算精度的影响不可忽略，这就需要寻找高阶MHM求解复合材料细观结构的物理和力学属性。Han等[26-27]基于二阶均匀化方法处理功能梯度材料的静态热力耦合问题，准确估计了有效弹性模量和应力应变场，并基于周期均匀化方法推导了用于求解复合材料弹性问题的二阶摄动项格式。Guan[20]和Cui[22]等给出了一种二阶多尺度方法用于预测周期复合材料的物理和力学属性，并应用于实际工程问题中。Allaire和Habibi[23]使用双尺度二阶渐进展开方法研究了具有辐射边界条件下的热传导模型，并证明了均匀化过程中的双尺度收敛。通过二阶摄动项可以更加准确地捕捉到材料内部物理和力学行为的细观信息，这一结论得到越来越多学者的认可，然而关于二阶摄动项的必要性问题基本上都是通过具体物理和力学问题的计算精度进行论证和说明，其结论往往不具有普遍性。
MHM本身是具有严密逻辑的数学方法，在处理力学领域具体工程问题时，如何从力学角度解释MHM是应用数学学者经常关心的问题，一旦能够研究清楚各阶摄动项的物理意义，无疑将有助于从力学角度确定合适的展开项数或阶次，避免一味追求高阶次或盲目舍弃高于某阶的项。Xing和Chen[28]在分析比较各种多尺度方法基础之上，针对线弹性平面问题揭示了MHM前三阶摄动项的物理意义，为该方法在数学和力学之间建立了联系，并通过物理意义的分析得到了二阶摄动项与一阶摄动项同为摄动主项的结论。除此之外，鲜有其他关于MHM物理意义研究的报道。相对于线弹性问题MHM物理意义的研究，热力耦合问题MHM各阶摄动项中同时包含弹性影响函数和热影响函数，以致出现更多、更复杂的虚拟载荷形式，其物理解释也变得复杂，然而确定热力耦合问题MHM的物理意义将有助于更好地理解和应用该方法处理具体的力学和物理问题，并且从物理机理的角度研究合适的展开阶次所得到的结论相对于通过具体力学和物理问题的研究所得到的结论更具有普遍性。
在此背景下，本文首先通过构造MHM各阶摄动项的全解耦格式，推导热力耦合问题MHM高阶摄动项的数学表达式及矩阵列式；其次将弹性影响函数和热影响函数分别比拟为弹性虚拟位移和热虚拟位移，利用热力耦合问题MHM矩阵列式实现方法、量纲分析方法和虚拟载荷自平衡性质，分别给出热特征位移和弹性特征位移的空间矢量图，再借助构造有限元位移场和温度场中广义坐标的概念，给出了各阶弹性虚拟位移、热虚拟位移和摄动项的物理意义，并通过物理意义的分析得到了二阶摄动项的必要性依据；最后通过数值算例和最小势能泛函计算结果验证了热力耦合问题MHM有限元矩阵列式推导和物理意义分析的正确性。
1. 热力耦合问题MHM的数学表达式和有限元矩阵列式
基于微观结构的周期性和单胞域的一致性假设，均匀化理论可以解耦成为微观结构异质边界值的单胞问题和宏观问题，对于结构线性小变形问题，热力耦合的应力-应变关系为
(1) 式中：σij为应力张量；Eijmn为弹性常数张量；上标ε代表结构中的不同材料；emntot为总应变；emnt为热应变。
总应变-位移和热应变分别表示为
(2) 
(3) 式中：uε为真实位移；amn为热膨胀系数；T为结构温差。
将式(2)和式(3)代入式(1)，并考虑弹性常数张量的对称性可以得到
(4) 二维周期复合材料控制方程为一致椭圆偏微分方程，其具有Dirichlet边界条件[29]：
(5) 真实位移umε的渐进展开形式为包含宏观尺度和微观尺度的函数：
(6) 式中：均匀化位移um0由均匀化结构计算得到，摄动位移umj(x, y)包含2个尺度，且在y上具有周期性；η为单胞尺寸和周期结构尺寸的比值。
文献[15]给出了一阶摄动项的全解耦格式和影响函数控制方程(包括弹性影响函数和热影响函数)，本文在此基础上推导了任意阶次摄动项的全解耦格式和影响函数控制方程，如表 1所示。影响函数仅与微观尺度相关且在y上具有周期性，宏观场(宏观位移场和温度场)及其各阶导数为宏观尺度x的函数；影响函数控制方程中的微分算子Δyj和Δyj·分别表示微观尺度y的散度和旋度，T(x)和aklε分别为结构温差函数和热膨胀系数。χ1mkl和ψ1m分别为一阶弹性影响函数和一阶热影响函数，χ2mklp和ψ2mp分别为二阶弹性影响函数和二阶热影响函数，以此类推。将影响函数比拟为虚拟位移，其中弹性影响函数比拟为弹性虚拟位移，热影响函数比拟为热虚拟位移，影响函数控制方程右端项对应为弹性虚拟载荷和热虚拟载荷，此时影响函数控制方程与一般结构平衡方程在形式上相同。从表 1中的摄动位移全解耦格式及影响函数控制方程可以得到以下结论：
表 1 摄动位移及影响函数控制方程Table 1. Perturbation displacements and governing equation of influence functions摄动位移 影响函数控制方程 
一阶弹性影响函数 
一阶热影响函数 
二阶弹性影响函数 
二阶热影响函数 
三阶弹性影响函数 
三阶热影响函数 
s阶弹性影响函数 
s阶热影响函数 
1) 一阶弹性影响函数控制方程右端项的Δyj·Eijklε和一阶热影响函数控制方程右端项的-Δyj·Eijklεaklε由单胞内材料参数所决定，与其他因素无关，且为分段集中虚拟载荷，分布在单胞内的基体和夹杂交界处，在单胞域内自平衡。
2) 二阶弹性影响函数控制方程右端项和二阶热影响函数控制方程右端项的虚拟载荷在单胞域内自平衡，其中Eipklε-EipklH和Eipklεaklε-EipklHaklH(EH和aH分别为均匀化弹性常数张量和均匀化热膨胀系数)只和材料本身相关，三阶及以上虚拟位移控制方程右端项不再包含仅和材料本身相关的项，均和低阶影响函数相关，而影响函数与单胞边界条件密切相关，所以可以得到一阶和二阶摄动项是摄动主项，不可忽略，即使用MHM处理周期复合材料热力耦合问题时需要摄动到二阶以保证计算精度。
3) 三阶及以上阶次影响函数控制方程具有相同的递推形式。
热力耦合问题MHM的应用分3步实施：①求解单胞问题，得到各阶热影响函数、弹性影响函数及均匀化材料参数EH和aH；②求解各阶宏观位移场导数和温度场导数；③求解MHM真实位移和应力。
表 1中各阶弹性影响函数和热影响函数控制方程的矩阵列式可以归纳为
(7) 式中：r=1, 2, …, a为展开阶次；Kε为单胞细观结构刚度矩阵；χr为弹性影响函数；ψr为热影响函数；FrE为弹性自平衡虚拟载荷；FrT为热自平衡虚拟载荷。
(8) 
(9) 
(10) 
(11) 式中：
(12) 其中：s=3, 4, 5…；e为单胞内的子单元数量；Ye表示单胞内子单元的区域；式(8)和式(9)中Eε表示周期结构内不同材料的弹性常数矩阵，式(10)和式(11)中的弹性常数矩阵在文献[28]附录A中给出；B为应变矩阵；χ为弹性影响函数矩阵；ψ为热影响函数矩阵；N为形函数矩阵；B、χ、ψ、N的维度取决于使用有限元(FEM)计算时所选择的单元阶次。
以线性矩阵单元为例，N为2×8矩阵，形式如下：
(13) 式中：Ni(i=1, 2, 3, 4)为单胞内子单元4个节点的形函数。此时B为3×8矩阵，与标准有限元方法形式相同；一阶影响函数χ1和ψ1分别为8×3矩阵和8×1矩阵，二阶影响函数χ2和ψ2分别为8×6矩阵和8×2矩阵，三阶影响函数χ3和ψ3分别为8×12矩阵和8×4矩阵，更高阶次影响函数矩阵的维度以此类推。
在表 1中，一阶弹性影响函数χ1mkl的上标k=1, 2和l=1, 2具有3种不同的组合方式，即kl=[11,22,12]，这3种组合方式分别与χ1的3列一一对应，χ2和χ3与之类似，上标klp=[111,221,121,112,222,122]，klpq=[1111,2211,1211,1121,2221,1221,1112,2212,1212,1122,2222,1222]分别对应χ2和χ3的6列和12列。热影响函数与弹性影响函数的上标形式相同，但意义不同，主要由于弹性常数矩阵包含泊松比，存在剪切作用，而热膨胀系数在平面问题中的2个方向具有相同的数值，即kl=11与kl=22相同且没有剪应变，是为了与弹性常数矩阵拥有相同的形式所构造的形式，即
(14) 所以ψ1mkl中的kl=[11]，即ψ1mkl只有1列，与ψ1mkl相似，ψ2mklp和ψ3mklpq分别依次对应上标klp=[111,112]和klpq=[1111,1121,1112,1122]的2列和4列。
结构由于热膨胀作用只产生线应变，剪应变为0，所以这种由于热变形产生的应变可以看作结构的初始应变ε0。对于二维问题，ε0的表达式为
(15) 所以均匀化宏观问题可以表达为
(16) 式中：f为外载荷。
在实际工程应用中，一般将一个单胞或多个单胞作为一个宏观单元处理，提高计算效率。
在得到宏观位移及其各阶导数、各阶温差场导数及摄动位移后，结构真实细观位移可以使用如下渐进展开表达式得到：
(17) 式中：∂u0/∂x、∂2u0/∂x2及∂3u0/∂x3分别与χ1、χ2和χ3的上标kl、klp和klpq的组合相对应求得；∂T/∂x和∂2T/∂x2分别与ψ2、ψ3的上标klp和klpq的组合相对应求得。
从以上求解公式可以看出，热力耦合问题MHM解耦形式都可以使用有限元方法得到。由式(17)可以看出，MHM的显著优点为细观尺度的解可以用宏观尺度来表示，这意味着在得到结构单胞的影响函数后，其计算精度取决于宏观位移、宏观位移场导数和宏观温度场导数的求解精度。
2. 热力耦合问题MHM的物理解释
从热力耦合问题MHM的计算公式和实现过程可以看出，其物理意义取决于弹性影响函数χr和热影响函数ψr，或用于求解影响函数控制方程右端项的自平衡虚拟载荷FrE和FrT。
在本文中，自平衡表示虚拟载荷在单胞域内的积分或者单胞内所有节点的虚拟载荷之和为0，FrE和FrT分别称为弹性虚拟载荷和热虚拟载荷，之所以称为虚拟载荷，是因为其在单胞内并非真实存在；从式(8)可以看出，Kε为单胞模型的刚度矩阵，所以χr和ψr可以看作与虚拟载荷相对应的虚拟位移矩阵，虚拟位移矩阵取决于虚拟载荷，而各阶虚拟载荷相互独立，且与结构外载荷及温差无关。
用于求解χ1的弹性自平衡虚拟载荷F1E的单位为N，单胞刚度矩阵Kε的单位为N/m，所以χ1的单位为m；同理可得，F2E的单位为N·m，χ2的单位为m2，F3E的单位为N·m2，χ3的单位为m3。用于求解ψ1的热自平衡虚拟载荷F1T的单位为N/K，所以ψ1的单位为m/K，同理可得，F2T的单位为N·m，ψ2的单位为m2/K，F3T的单位为N·m2，ψ3的单位为m3/K。
2.1 二维周期复合材料单胞结构
对于单胞模型内部一个线性子单元，用于求解一阶弹性影响函数χ1的弹性自平衡虚拟载荷形式为
(18) 式中：ν为泊松比；l1和l2分别为矩形子单元沿着坐标轴x1和x2方向的长度。显然，如果l1=l2或c=1，即正方形子单元，F1的第1列(与kl=11相对应)中每个节点沿着坐标轴x1和x2方向的比值为±1/ν，第2列(与kl=22相对应)中每个节点沿着坐标x1和x2方向的比值为±ν，第3列(与kl=12相对应)中每个节点沿着坐标x1和x2方向的比值为±1。
同理，对于单胞模型内部一个线性子单元，用于求解一阶弹性影响函数ψ1的热自平衡虚拟载荷形式为
(19) 显然，如果l1=l2或c=1，即正方形子单元，F1T中的每个节点沿着坐标轴x1和x2方向的比值为±1。
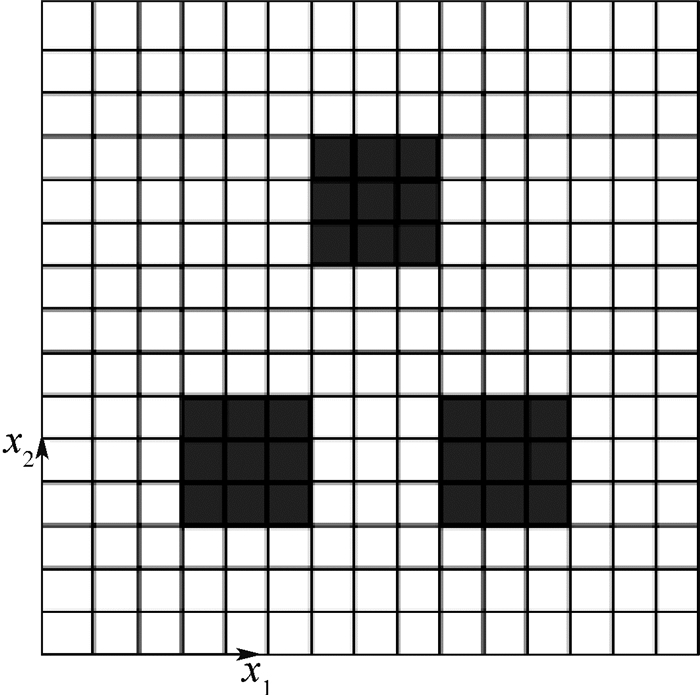
图 1为包含3块夹杂的二维单胞细分网格模型。为了更加清晰地给出虚拟载荷矩阵中每一列矢量图，在本文中选取夹杂和基体的弹性模量分别为50 GPa和60 GPa，热膨胀系数分别为1.5×10-6/℃和1×10-6/℃，泊松比均为0.2。前三阶虚拟载荷和影响函数的物理意义讨论如下：
图 1 包含3块夹杂的二维周期复合材料单胞结构Figure 1. 2D periodical composites unit cell structures with 3 inclusions1) F1T和F1E，ψ1和χ1
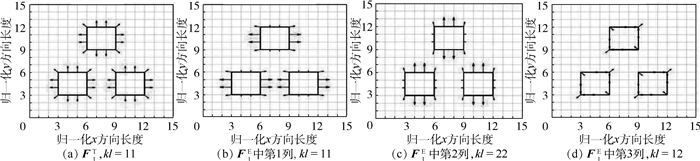
在文献[28]中，针对线弹性问题MHM分别给出了包含1块夹杂单胞结构和包含4块夹杂单胞结构的F1E矢量分布图。所以在本文中，针对热力耦合问题MHM给出包含3块夹杂单胞结构的F1T和F1E矢量示分布，如图 2所示。图 2(a)对应F1T矩阵的1列，图 2(b)~(d)分别对应F1E矩阵的3列，可以得到:
① 只要夹杂的材料性质相同，在每一块夹杂上相同位置节点上的矢量都是相同的，这个结论普遍成立，与单胞包含夹杂的数量无关。
② F1T和F1E是由单胞的材料属性所决定的，而与边界条件无关，如式(18)和式(19)所示，F1E矩阵所包含的3列可以看成是3种相互独立的分段线性载荷作用在平面结构上，而F1T矩阵所包含的1列可以看成是1个独立的分段线性载荷作用在平面结构上。
③ ψ1和χ1反映了单胞内材料的不连续性，因为它们是由分布在夹杂和基体交界处节点的分段线性载荷计算得到的。另一方面也反映了夹杂和基体之间的相互作用，是单胞内材料不均匀性的最基本关系，因为在基体和夹杂的内部节点是没有载荷作用的。
④ u1为一阶摄动主项，本质上是χ1矩阵的3列和ψ1的1列虚拟位移的线性组合，所以一般来说，如果基体和夹杂的弹性模量、热膨胀系数相差不大时，使用MHM处理周期结构复合材料热力耦合问题摄动到一阶的精度就足够了。
2) F2T和F2E，ψ2和χ2
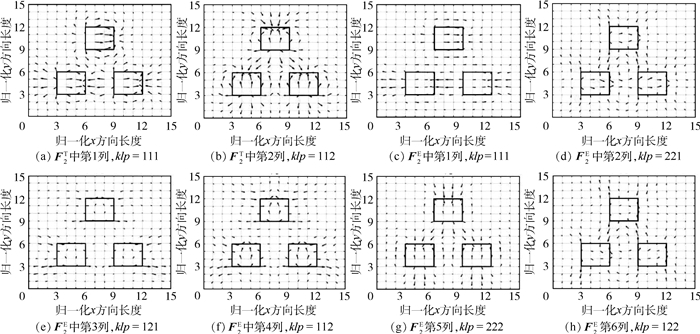
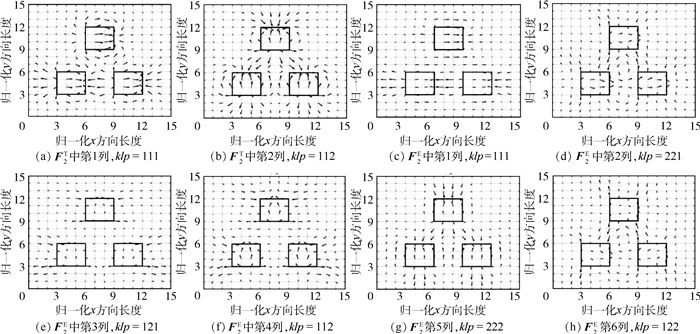
图 3给出了用于求解二阶影响函数的虚拟载荷矢量示意图。图 3(a)、(b)分别对应F2T的2列向量，即klp=111，112；图 3(c)~(h)依次分别对应F2E矩阵中的6列向量，即klp=111，221，121，112，222和122。
① F2T和F2E矩阵表达式中的第一项中所包含的均匀化弹性常数张量EH、均匀化热膨胀系数aH、材料的弹性模量Eε及材料的热膨胀系数aε与单胞边界条件无关，如式(10)所示，所以u2和u1一样同为主项而不可忽略。F2E和F2T矩阵表达式中的第2项分别与χ1和ψ1有关，即与单胞边界条件相关。
② F2T和F2E是面载荷，在基体和夹杂内部均不为0，所以相对于F1T和F1E刻画了更详细的细观信息，而由F2T和F2E分别计算得到的ψ2和χ2反映了单胞内基体与夹杂及基体内部、夹杂内部复杂的相互关系。
3) F3T和F3E，ψ3和χ3
图 4给出了用于求解三阶影响函数的虚拟载荷矢量示意图。图 4(a)~(d)依次分别对应F3T矩阵的4列向量，即klpq=1111, 1121, 1112, 1122；图 4(e)~(p)依次分别对应F3E矩阵中的12列向量，即klpq=1111，2211，1211，1121，2221，1221，1112，2212，1212，1122，2222，1222。从式(11)可以看出，F3E与F1E、F2E及F3T与F1T、F2T的明显不同就是F3E的矩阵表达式中同时含有χ1和χ2，F3T的矩阵表达式中同时含有ψ1和ψ2，即完全与单胞的边界条件联系在一起。从矢量示意图可以看出，F3E和F3T要比F2E和F2T更加复杂，刻画了更加详细的细观信息，因为所有节点上的矢量在2个方向上均不为0，所以χ3和ψ3也就能够反映单胞内部材料之间复杂的相互关系。综合来说，u3主要由u1和u2构成且与单胞边界条件密切相关，所以u3可以认为是高阶摄动项。从式(11)可以得到，当s≥3时，虚拟载荷矩阵表达式都有相同的递推形式，所以更高阶摄动项都可以有类似的解释。
综合前三阶虚拟载荷矢量示意图可以得到以下结论：
1) 一阶弹性影响函数χ1和一阶热影响函数ψ1反映的是单胞内基体和夹杂之间的相互作用的结果，一阶摄动项u1是χ1矩阵中3列向量和ψ1的线性组合，反映单胞细观信息的位移场；包含一阶摄动项的MHM计算精度对于基体和夹杂之间弹性模量和热膨胀系数相差不大的情况下是足够精确的。
2) F2E和F2T矩阵表达式中的第1项只包含均匀化弹性模量及材料的热膨胀系数，与单胞边界条件无关，而第2项及F2E、F2T(r≥3)都和单胞边界条件相关，所以二阶摄动项与一阶摄动项均为主项。
3) 一阶影响函数χ1和ψ1反映了基体内部、夹杂内部及基体和夹杂相互作用的结果，二阶摄动项u2是χ2矩阵中6列向量线性组合与ψ2矩阵中2列向量线性组合的和，反映单胞内材料更加准确的细观信息，所以对于一般周期复合材料而言，包含二阶摄动项的MHM的计算精度是足够的，但对于单胞内的基体和夹杂材料参数相差特别大的周期复合材料，极限情况下，如具有孔洞的周期结构，将孔洞视为夹杂，则基体和夹杂的材料弹性模量比例无限大，或某些颗粒增强结构，基体和夹杂的弹性模量比值无限小，此时包含二阶摄动项的计算精度是否足够需要专门研究。
2.2 周期复合材料杆单胞结构
文献[28]中给出了线性单元杆单胞弹性虚拟载荷和弹性特征位移分析结果，本文使用二次单元分析杆单胞的弹性影响函数和热影响位移，以及与之相对应的弹性虚拟载荷和热虚拟载荷。
考虑包含一块夹杂的杆单胞，如图 5所示，对于这样简单的问题可以推导出其解析解形式。使用3个二次杆单元计算该单胞模型，该情况下，m=k=l=p=q=1。E1和E2分别表示基体和夹杂的弹性模量，a1和a2分别为基体和夹杂的热膨胀系数，L为单元长度，A为横截面积。
图 5 包含一块夹杂的周期复合材料杆单胞结构Figure 5. Periodical composites rod unit cell structure with one inclusion针对图 5中的一个子单元，各阶影响函数控制方程如下：
1) 一阶热影响函数控制方程
(20) 2) 一阶弹性影响移函数控制方程
(21) 式中：(χ1111)和(ψ1111)的下标1、2和3分别表示子单元的左、中和右节点；下标g为1或2，分别代表基体和夹杂。
从式(20)和式(21)可以看出，其右端项只有虚拟集中载荷AEiai和AEi，使用固支边界条件且根据节点位移协调条件，则(χ1111)11=(χ1111)23=0, (χ1111)12=(χ1111)21, (χ1111)22=(χ1111)13，装配3个单元分别得到单胞结构的弹性影响函数控制方程和热影响函数控制方程为
(22) 
(23) 分别求解方程可得到单胞结构弹性影响函数和热影响函数为
(24) 
(25) 式中：
值得注意的是，当相邻2个单元的弹性模量、热膨胀系数均相同时，即均质材料，式(24)右端项为0，同时对于非均质材料，若耦合参数相同(E2a2=E1a1)时，方程右端项也为0；对比式(25)，弹性自平衡虚拟载荷只有在不同弹性模量交界处才非0，即非均质材料，而热自平衡虚拟载荷只有在不相同耦合模量交界处才非0，基体和夹杂内部没有虚拟载荷，所以一阶虚拟载荷反映的是基体和夹杂之间的相互作用，是反映单胞内部结构最基本的信息载体。
式(12)、式(24)、式(25)联立，可得得到均匀化弹性模量和均匀化热膨胀系数分别为
(26) 二阶热虚拟载荷和弹性虚拟载荷分别为
(27) 二阶弹性影响函数和热影响函数分别为
(28) 三阶热虚拟载荷和弹性虚拟载荷分别为
(29) 三阶热影响函数和弹性影响函数分别为
(30) 从二阶虚拟载荷和三阶虚拟载荷形式可以看出，当弹性模量相同时，弹性虚拟载荷为0，当耦合参数相同时，热虚拟载荷为0，即在非均质材料交界处，弹性虚拟载荷一定非0，而热虚拟载荷可能为0，所以弹性问题只考虑不同材料之间弹性参数的异同，而热问题需要同时考虑弹性参数和热膨胀系数；另一方面，弹性虚拟载荷和热虚拟载荷在单元内部节点不为0，所以二阶和三阶虚拟载荷除了反映基体和夹杂之间的相互作用，也刻画了基体和夹杂内部更加详细的细观信息。
3. 数值分析
3.1 二维周期复合材料单胞结构
结构大小为15 mm×15 mm，单胞内含有4块夹杂，如图 6所示。基体的弹性模量和热膨胀系数分别为E1=2×109 Pa, a1=3×10-6/℃，夹杂的弹性模量和热膨胀系数分别为E2=6×1010 Pa, a2=1×10-6/℃，基体和夹杂的泊松比均为ν=0.2，结构温差T=16(x2+y2)。
分别使用式(12)计算得到均匀化弹性模量和均匀化热膨胀系数分别为EH=2.67×109 Pa, aH=2.5×10-6/℃。图 7给出了结构沿A、B、C、D上节点在x1方向的位移曲线。表 2给出了结构总势能泛函Π计算结果，其中FEM为有限元解，作为标准检验MHM的求解精度，MHM1表示包含一阶摄动项的计算结果，MHM2表示包含二阶摄动项的计算结果，MHM3表示包含三阶摄动项的计算结果。结合图 7和表 2可以得到：①包含一阶摄动位移的计算结果MHM1误差较大；②MHM2和MHM3的精度明显高于MHM1；③MHM3精度高于MHM2。
图 7 沿纵线A、B、C、D上节点位移曲线Figure 7. Nodal displacement curves along longitudinal lines A, B, C and D表 2 二维周期复合材料单胞结构的势能泛函Table 2. Potential energy function for 2D periodical composites unit cell摄动位移 Π/(10-6J) 
MHM FEM MHM1 -2.475 15.8 MHM2 -2.916 -2.939 0.78 MHM3 -2.937 0.068 3.2 二维周期复合材料多胞结构
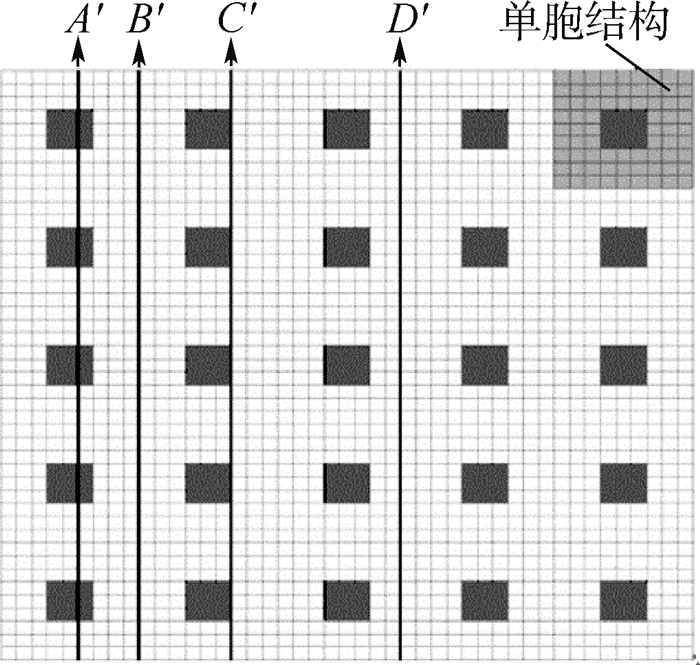
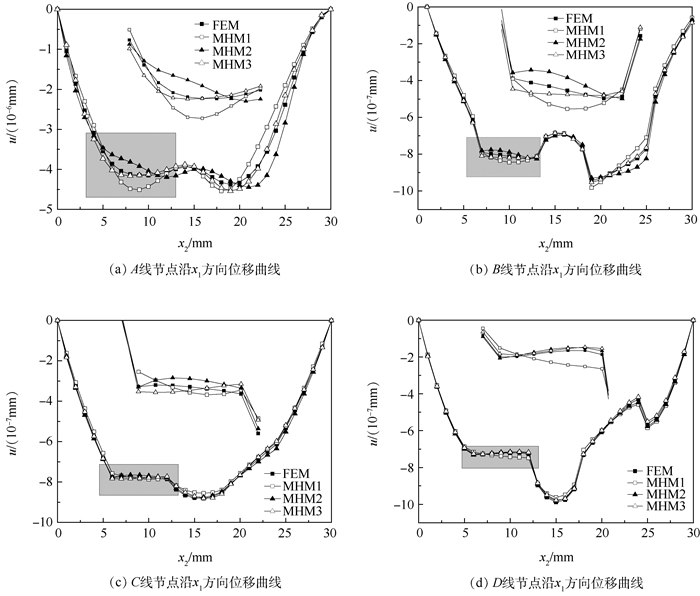
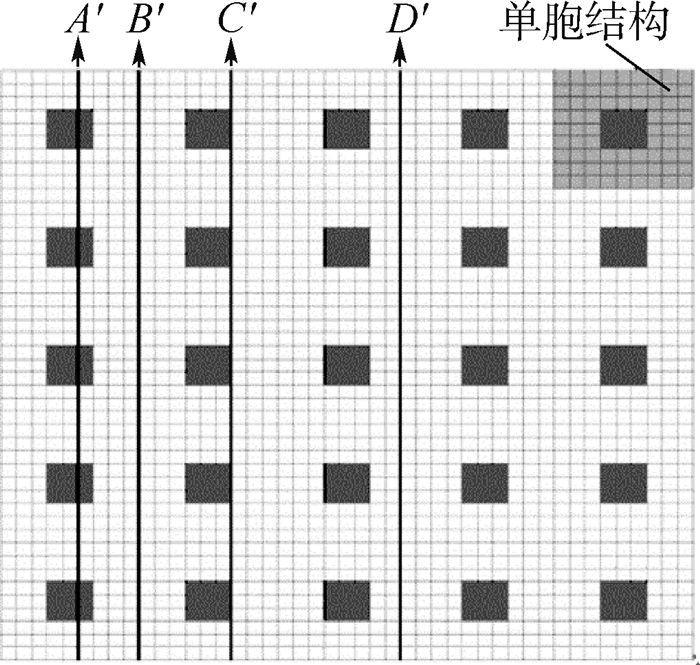
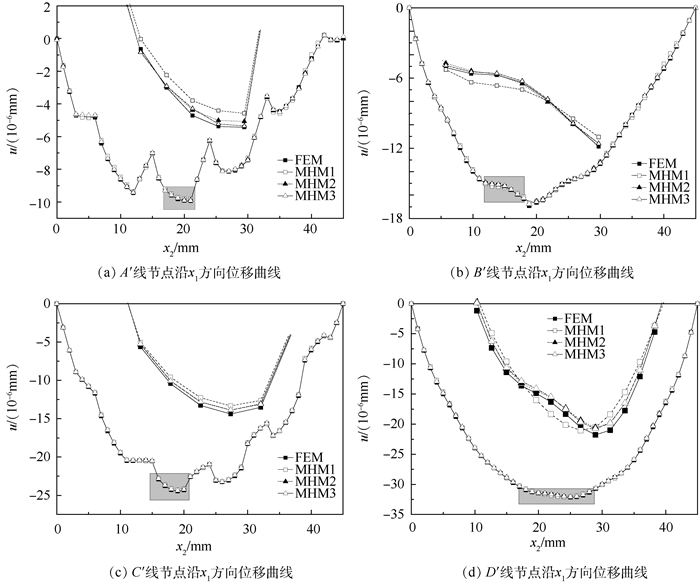
结构大小为45 mm×45 mm，包含5×5个单胞，每个单胞内部含有一块夹杂，如图 8所示，材料参数及温差和3.1节相同。影响函数和宏观位移导数分别使用超单胞周期边界条件和微分求积有限单元法[30]计算得到，均匀化弹性模量和均匀化热膨胀系数分别为EH=2.42×109 Pa, aH=2.63×10-6/℃。表 3给出了结构的总势能泛函计算结果，FEM、MHM1、MHM2、MHM3的含义与3.1节相同。图 9给出了结构沿A′、B′、C′、D′上节点x1方向的位移曲线。结合图 9和表 3可以得到：①包含一阶摄动位移的计算结果MHM1误差较大；②MHM2和MHM3的计算精度明显好于MHM1；③MHM2和MHM3的计算精度较高，且两者相差不大；④二阶摄动项对计算精度的影响较大，而三阶摄动项对计算精度的影响可以忽略。
表 3 二维周期复合材料多胞结构的势能泛函Table 3. Potential energy function for 2D periodical composite multi-cell structure摄动位移 Π/(10-8J) 
MHM FEM MHM1 -3.547 7 20 MHM2 -4.335 6 -4.436 1 2.27 MHM3 -4.396 8 0.89 
图 9 沿纵线A′、B′、C′、D′上节点位移曲线Figure 9. Nodal displacement curves along longitudinal lines A′, B′, C′ and D′4. 结论
本文通过构造摄动项的全解耦格式推导了热力耦合问题高阶MHM的数学表达式和有限元矩阵列式，将弹性影响函数和热影响函数分别比拟为弹性虚拟位移和热虚拟位移，利用虚拟载荷的自平衡性质、量纲分析和空间矢量分布揭示了各阶摄动项的物理意义；数值算例分析证明了公式推导结果和物理意义分析的正确性。通过热力耦合问题MHM各阶摄动项物理意义的分析和数值计算结果，给出了二阶摄动项对于周期复合材料计算精度的必要性依据，为热力耦合问题MHM的应用奠定了力学基础。
-
图 1 包含3块夹杂的二维周期复合材料单胞结构
Figure 1. 2D periodical composites unit cell structures with 3 inclusions
图 5 包含一块夹杂的周期复合材料杆单胞结构
Figure 5. Periodical composites rod unit cell structure with one inclusion
图 7 沿纵线A、B、C、D上节点位移曲线
Figure 7. Nodal displacement curves along longitudinal lines A, B, C and D
图 9 沿纵线A′、B′、C′、D′上节点位移曲线
Figure 9. Nodal displacement curves along longitudinal lines A′, B′, C′ and D′
表 1 摄动位移及影响函数控制方程
Table 1. Perturbation displacements and governing equation of influence functions
摄动位移 影响函数控制方程 
一阶弹性影响函数 
一阶热影响函数 
二阶弹性影响函数 
二阶热影响函数 
三阶弹性影响函数 
三阶热影响函数 
s阶弹性影响函数 
s阶热影响函数 
下载: 导出CSV
表 2 二维周期复合材料单胞结构的势能泛函
Table 2. Potential energy function for 2D periodical composites unit cell
摄动位移 Π/(10-6J) 
MHM FEM MHM1 -2.475 15.8 MHM2 -2.916 -2.939 0.78 MHM3 -2.937 0.068
下载: 导出CSV
表 3 二维周期复合材料多胞结构的势能泛函
Table 3. Potential energy function for 2D periodical composite multi-cell structure
摄动位移 Π/(10-8J) 
MHM FEM MHM1 -3.547 7 20 MHM2 -4.335 6 -4.436 1 2.27 MHM3 -4.396 8 0.89
下载: 导出CSV
-
[1] BERTHELOT J M. Composite materials:Mechanical behavior and structural analysis[M]. New York:Springer, 1999. [2] KALIDINDI S R, ABUSAFIEH A.Longitudinal and transverse moduli and strengths of low angle 3-D braided composites[J]. Journal of Composite Materials, 1996, 30(8):885-905. doi: 10.1177/002199839603000802 [3] BABUSKA I.Solution of interface problems by homogenization, Parts I[J]. SIAM Journal on Mathematical Analysis, 1976, 7(5): 603-634. doi: 10.1137/0507048 [4] BENSSOUSAN A, LIONS J L.Asymptotic analysis for periodic structures[M]. Amsterdam:North-Holland, 1978. [5] STROUBOULIS T, BABUSKA I, COPPS K.The generalized finite element method:An example of its implementation and illustration of its performance[J]. International Journal for Numerical Methods in Engineering, 2000, 47(8):1401-1417. doi: 10.1002/(SICI)1097-0207(20000320)47:8<1401::AID-NME835>3.0.CO;2-8 [6] BABUSKA I, OSBOM J.Generalized finite element methods:Their performance and their relation to mixed methods[J]. SIAM Journal on Numerical Analysis, 1983, 20(3):510-536. doi: 10.1137/0720034 [7] HOU T Y, WU X H.A multiscale finite element method for elliptic problems in composite materials and porous media[J]. Journal of Computational Physics, 1997, 134(1):169-189. [8] HOU T Y, WU X H, CAI Z Q.Convergence of a multiscale finite element method for elliptic problems with rapidly oscillating coefficients[J]. Mathematics of Computation, 1999, 68(227):913-943. doi: 10.1090/S0025-5718-99-01077-7 [9] E W, ENGQUIST B.The heterogeneous multiscale methods[J]. Communications in Mathematical Sciences, 2003, 1:87-132. doi: 10.4310/CMS.2003.v1.n1.a8 [10] E W, ENGQUIST B, LI X T, et al.Heterogeneous multiscale methods:A review[J]. Communications in Computational Physics, 2007, 2(3):367-450. [11] XING Y F, YANG Y.An eigenelement method of periodical composite structures[J]. Composite Structures, 2011, 93(2):502-512. doi: 10.1016/j.compstruct.2010.08.029 [12] XING Y F, YANG Y, WANG X M.A multiscale eigenelement method and its application to periodical composite structures[J]. Composite Structures, 2010, 92:2265-2275. doi: 10.1016/j.compstruct.2009.08.006 [13] TERADA K, KURUMATANI M, USHIDAI N, et al.A method of two-scale thermo-mechanical analysis for porous solids with micro-scale heat transfer[J]. Computational Mechanics, 2010, 46(2):269-285. [14] MUHAMMAD R, ERDATA N, NAOYUKI W, et al.A novel asymptotic expansion homogenization analysis for 3-D composite with relieved periodicity in the thickness direction[J]. Composites Science and Technology, 2014, 97:63-73. doi: 10.1016/j.compscitech.2014.04.006 [15] MUHAMMAD R, ERDATA N, NAOYUKI W, et al.Thermomechanical properties and stress analysis of 3-D textile composites by asymptotic expansion homogenization method[J]. Composites Part B:Engineering, 2014, 60:378-391. doi: 10.1016/j.compositesb.2013.12.038 [16] BARROQUEIRO B, DIAS-DE-OLIVEIRA J, PINHO-DA-CRUZ J, et al.Practical implementation of asymptotic expansion homogenizationin thermoelasticity using a commercial simulation software[J]. Composite Structures, 2016, 141:117-131. doi: 10.1016/j.compstruct.2016.01.036 [17] ZHAI J J, CHENG S, ZENG T, et al.Thermo-mechanical behavior analysis of 3D braided composites by multiscale finite element method[J]. Composite Structures, 2017, 176:664-672. doi: 10.1016/j.compstruct.2017.05.064 [18] 李志青, 冯永平.一类小周期结构热力耦合问题的双尺度渐近分析[J].广州大学学报, 2016, 15(2):27-32.LI Z Q, FENG Y P.Two-scale asymptotic analysis on one class of thermoelastic coupling problem in small periodic structure[J]. Chinese Journal of Guangzhou University, 2016, 15(2):27-32(in Chinese). [19] YANG Z Q, CUI J Z, ZHOU S.Thermo-mechanical analysis of periodic porous materials with microscale heat transfer by multiscale asymptotic expansion method[J]. International Journal of Heat and Mass Transfer, 2016, 92:904-919. doi: 10.1016/j.ijheatmasstransfer.2015.09.055 [20] GUAN X F, LIU X, JIA X, et al.A stochastic multiscale model for predicting mechanical properties of fiber reinforced concrete[J]. International Journal of Solids and Structures, 2015, 56-57:280-289. doi: 10.1016/j.ijsolstr.2014.10.008 [21] YANG Z Q, CUI J Z, MA Q.The second-order two-scale computation for integrated heat transfer problem with conduction, convection and radiationin periodic porous materials[J]. Discrete and Continous Dynamical System-Series B, 2014, 19(3):827-848. doi: 10.3934/dcdsb.2014.19.827 [22] YANG Z Q, SUN Y, CUI J Z.A multiscale algorithm for heat conduction-radiation problems in porous materials with quasi-periodic structures[J]. Communications in Computational Physics, 2018, 24(1):204-233. [23] ALLAIRE G, HABIBI Z.Second order corrector in the homogenization of a conductive-radiative heat transfer problem[J]. Discrete and Continuous Dynamical System-Series B, 2013, 18(1): 1-36. [24] WAN X, CAO L Q, WONG Y S.Multiscale computation and convergence for coupled thermoelastic system in composite materials[J]. Multiscale Model & Simulation, 2015, 13(2):661-690. [25] YANG Z Q, CUI J Z, SUN Y, et al.Multiscale analysis method for thermo-mechanical performance of periodic porous materials with interior surface radiation[J]. International Journal for Numerical Methods in Engineering, 2016, 105(5):323-350. doi: 10.1002/nme.4964 [26] HAN F, CUI J Z, YU Y.The statistical second-order two-scale method for thermomechanical properties of statistically inhomogeneous materials[J]. Computational Materials Science, 2009, 46(3):654-659. doi: 10.1016/j.commatsci.2009.03.026 [27] HAN F, CUI J Z, YU Y.The statistical second-order two-scale method for mechanical properties of statistically inhomogeneous materials[J]. International Journal for Numerical Methods in Engineering, 2010, 84(8):972-988. doi: 10.1002/nme.2928 [28] XING Y F, CHEN L.Physical interpretation of multi-scale asymptotic expansion method[J]. Composite Structures, 2014, 116:694-702. doi: 10.1016/j.compstruct.2014.06.004 [29] 郑健龙, 李友云, 钱国平.多尺度计算方法-均匀化和平均化[M].北京:科学出版社, 2010.ZHENG J L, LI Y Y, QIAN G P.Multi-scale calculation methods-homogenization and averaging[M]. Beijing:Science Press, 2010(in Chinese). [30] XING Y F, GAO Y H, CHEN L, et al.Solution methods for two key problems in multiscale asymptotic expansion method[J]. Composite Structures, 2017, 160:854-866. doi: 10.1016/j.compstruct.2016.10.104 期刊类型引用(1)
1. 贾学增，王正，冉隆毅. 热力耦合模拟钛合金压力容器疲劳失效分析. 兵器材料科学与工程. 2020(04): 122-126 . 
百度学术其他类型引用(1)
-
下载:
下载:
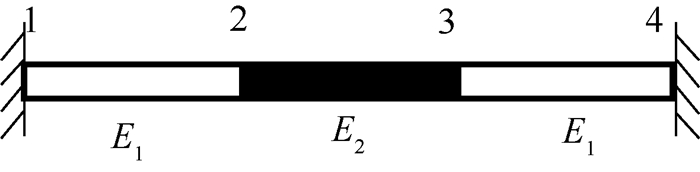
百度学术
点击查看大图
计量
- 文章访问数: 722
- HTML全文浏览量: 21
- PDF下载量: 387
- 被引次数: 2
