Effect of low-speed modification of compressible solver on turbulence simulation accuracy
-
摘要:
修正可压缩求解器能提高其对高速湍流中低速区的模拟精度，但低速修正效果受到求解器、计算格式精度、网格量等多因素影响，难以直接评估。研究了不同阶数、分辨率、网格量下，有无低速修正的可压缩求解器对复杂湍流模拟的影响。通过泰勒-格林涡算例，定量分析了不同结果的差异。结果表明：不同网格量、计算方法组合下，低速修正对结果的影响不同。网格量较小、重构格式精度较低的情况下，低速修正方法能够有效提高计算精度。
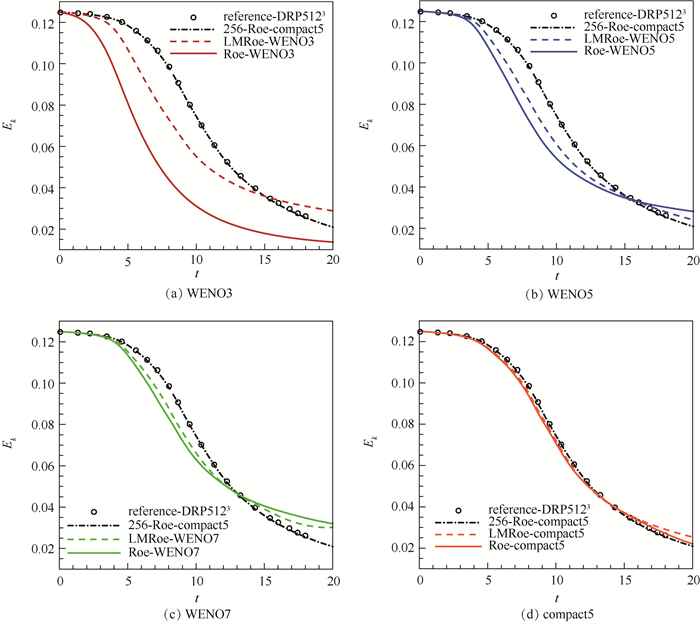
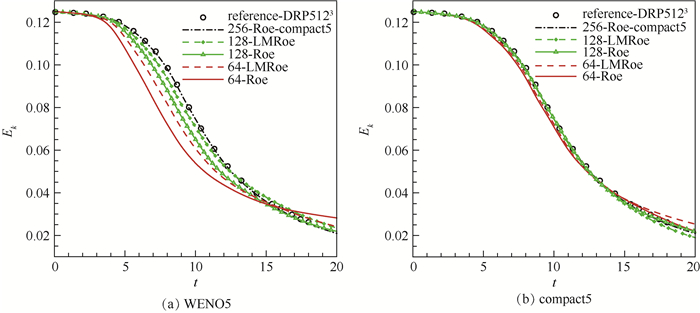
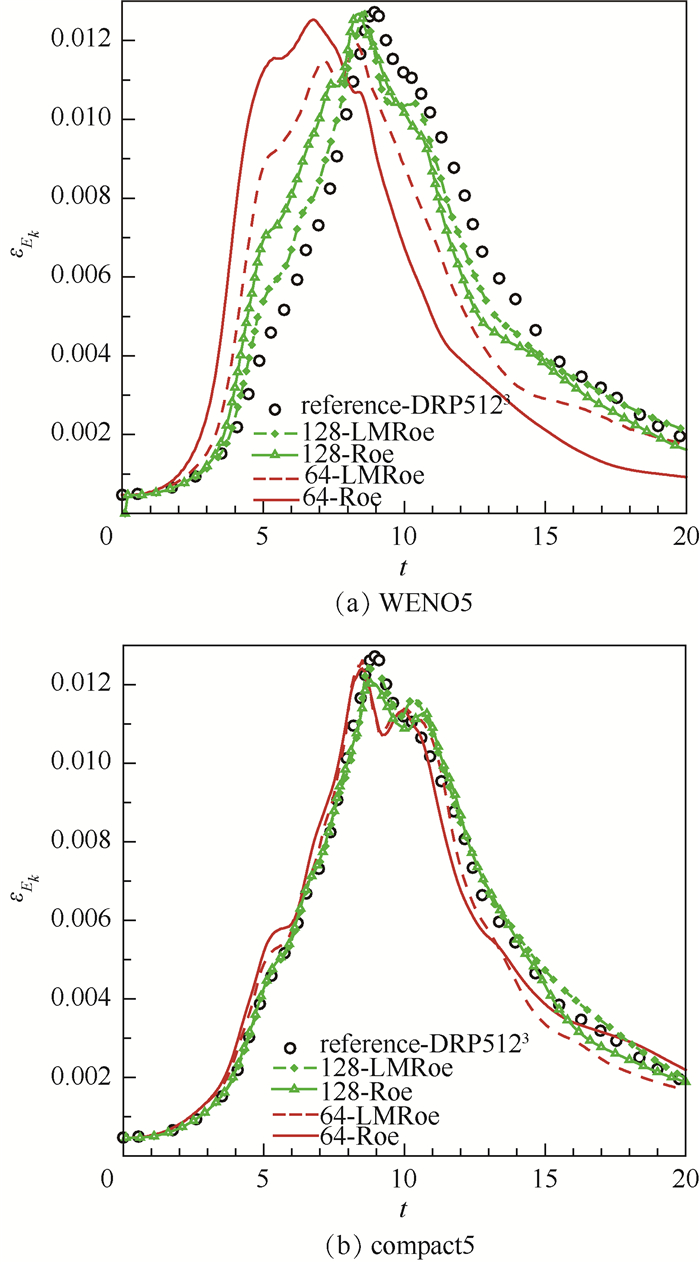
Abstract:The calculation accuracy of low-speed region in high speed turbulence can be improved by modifying the compressible solver. However, it is difficult to evaluate the contribution of such modification, because simulation accuracy results from complex factors including solver type, accuracy of schemes, grid number, etc. This paper focuses on the influence of the compressible solver with and without low-speed modification on complex turbulence simulation when using different order or resolution of the schemes and different amount of grid. With the calculation example of Taylor-Green vortex, the differences of the results are evaluated quantitatively. The results show that the influence of the low-speed modification is different with different scheme-grid combinations. The low-speed modification method can effectively improve the calculation accuracy with coarse grids and low-accuracy reconstruction schemes.
-
图 1 不同重构格式的分辨率特性曲线
Figure 1. Resolution properties of different reconstruction schemes
图 2 体平均动能随时间变化曲线(网格间距2π/64)
Figure 2. Variation of volume-averaged kinetic energy with time under grid space 2π/64
图 3 动能耗散率随时间变化曲线(网格间距2π/64)
Figure 3. Variation of energy dissipation rate with time under grid space 2π/64
图 4 体平均动能随时间变化曲线(网格间距2π/64和2π/128)
Figure 4. Variation of volume-averaged kinetic energy with time (grid space 2π/64 and 2π/128)
图 5 动能耗散率随时间变化曲线(网格间距2π/64和2π/128)
Figure 5. Variation of energy dissipation rate with time (grid space 2π/64 and 2π/128)
图 6 不同格式和网格量下体平均动能误差柱状图
Figure 6. Histogram of volume-averaged kinetic energy error for different schemes with different grids
图 7 不同格式和网格量下动能耗散率误差柱状图
Figure 7. Histogram of energy dissipation rate error for different schemes with different grids
图 8 不同网格量下Roe和LMRoe通量格式的计算差异(体平均动能)
Figure 8. Calculation difference of Roe and LMRoe flux schemes with different amounts of grid (volume-averaged kinetic energy)
图 9 不同网格量下Roe和LMRoe通量格式的计算差异(动能耗散率)
Figure 9. Calculation difference of Roe and LMRoe flux schemes with different amounts of grid (energy dissipation rate)
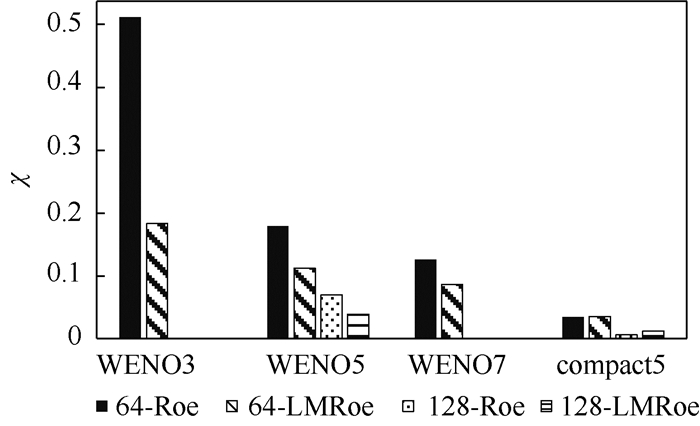
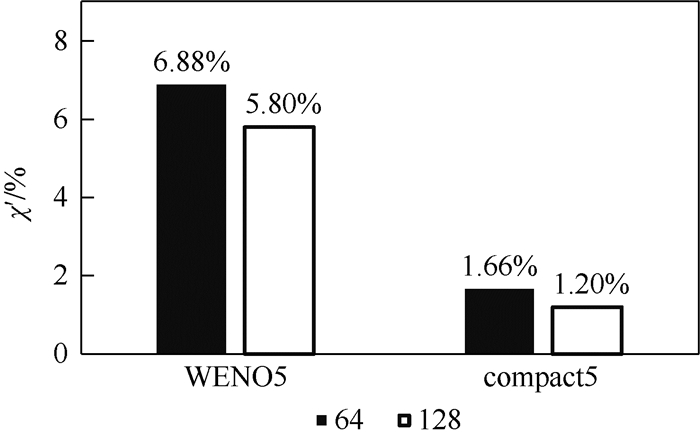
表 1 网格间距2π/64时不同通量格式结果的误差比值
Table 1. Ratio of two flux schemes' result errors with grid space being 2π/64
重构格式 体平均动能 动能耗散率 WENO3 0.36 0.57 WENO5 0.63 0.61 WENO7 0.69 0.75 compact5 1.04 1.00 
下载: 导出CSV
表 2 网格间距2π/128时不同通量格式结果的误差比值
Table 2. Ratio of two flux schemes' result errors with grid space being 2π/128
重构格式 体平均动能 动能耗散率 WENO5 0.56 0.57 compact5 1.85 0.76
下载: 导出CSV
-
[1] 傅德薰, 马延文, 李新亮, 等.可压缩湍流直接数值模拟[M].北京:科学出版社, 2010.FU D X, MA Y W, LI X L, et al.Direct numerical simulations for compressible turbulence[M].Beijing:Science Press, 2010(in Chinese). [2] 屈峰.高分辨率格式的研究及其应用[D].北京: 北京航空航天大学, 2015.QU F.Research and application of high resolution schemes[D].Beijing: Beihang University, 2015(in Chinese). [3] WEISS J M, SMITH W A.Preconditioning applied to variable and constant density flows[J].AIAA Journal, 1995, 33(11):2050-2057. doi: 10.2514/3.12946 [4] LIOU M S.A sequel to AUSM.Part Ⅱ:AUSM+-up for all speeds[J].Journal of Computational Physics, 2006, 214(1):137-170. doi: 10.1016-j.jcp.2005.09.020/ [5] KITAMURA K, SHIMA E.Towards shock-stable and accurate hypersonic heating computations:A new pressure flux for AUSM-family schemes[J].Journal of Computational Physics, 2013, 245:62-83. doi: 10.1016/j.jcp.2013.02.046 [6] RIEPER F.A low-Mach number fix for Roe's approximate Riemann solver[J].Journal of Computational Physics, 2011, 230(13):5263-5287. doi: 10.1016/j.jcp.2011.03.025 [7] FILLION P, CHANOINE A, DELLACHERIE S, et al.FLICA-OVAP:A new platform for core thermal-hydraulic studies[J].Nuclear Engineering and Design, 2011, 241(11):4348-4358. doi: 10.1016/j.nucengdes.2011.04.048 [8] LI X, GU C.An all-speed roe-type scheme and its asymptotic analysis of low Mach number behaviour[J].Journal of Computational Physics, 2008, 227(10):5144-5159. doi: 10.1016/j.jcp.2008.01.037 [9] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社, 2006.YAN C.Method and application of computational fluid dynamics[M].Beijing:Beihang University Press, 2006(in Chinese). [10] GOTTLIEB S, SHU C W.Total variation diminishing Runge-Kutta schemes[J].Mathematics of computation of the American Mathematical Society, 1998, 67(221):73-85. doi: 10.1090/S0025-5718-98-00913-2 [11] ROE P L.Approximate Riemann solvers, parameter vectors, and difference schemes[J].Journal of Computational Physics, 1997, 135(2):250-258. doi: 10.1006/jcph.1997.5705 [12] JIANG G, SHU C.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126(1):202-228. doi: 10.1006/jcph.1996.0130 [13] PIROZZOLI S.On the spectral properties of shock-capturing schemes[J].Journal of Computational Physics, 2006, 219(2):489-497. doi: 10.1016/j.jcp.2006.07.009 [14] FAUCONNIER D, DICK E.On the spectral and conservation properties of nonlinear discretization operators[J].Journal of Computational Physics, 2011, 230(12):4488-4518. doi: 10.1016/j.jcp.2011.02.025 [15] BRACHET M E, MEIRON D I, ORSZAG S A, et al.Small-scale structure of the Taylor-Green vortex[J].Journal of Fluid Mechanics, 1983, 130:411-452. doi: 10.1017/S0022112083001159 [16] DEBONIS J.Solutions of the Taylor-Green vortex problem using high-resolution explicit finite difference methods: AIAA-2013-0382[R].Reston: AIAA, 2013. -
下载:
点击查看大图
计量
- 文章访问数: 554
- HTML全文浏览量: 44
- PDF下载量: 295
- 被引次数: 0
