基于随机相关的电子部件二元加速退化可靠性评估

盖炳良; 滕克难; 王浩伟; 王文双; 陈健; 宦婧

doi:10.13700/j.bh.1001-5965.2019.0130

基于随机相关的电子部件二元加速退化可靠性评估

doi: 10.13700/j.bh.1001-5965.2019.0130

盖炳良^{1, 2},
滕克难^1, ,,
王浩伟¹,
王文双¹,
陈健¹,
宦婧³

1.
海军航空大学烟台 264001
2.
中国人民解放军 91115部队, 舟山 316000
3.
江苏科技大学计算机学院, 镇江 212003

基金项目:

国家自然科学基金 51605487

详细信息

作者简介:
盖炳良男, 博士研究生。主要研究方向:装备可靠性评估、加速试验技术等

滕克难男, 博士, 教授, 博士生导师。主要研究方向:装备延寿理论与技术

通讯作者:
滕克难.E-mail:Tengkn@sina.com

中图分类号: TB114.3
计量
- 文章访问数: 745
- HTML全文浏览量: 99
- PDF下载量: 427
- 被引次数: 0
出版历程
- 收稿日期: 2019-03-27
- 录用日期: 2019-05-28
- 网络出版日期: 2019-11-20

Reliability assessment for electronic components with bivariate accelerated degradation based on random correlation

1.
Naval Aviation University, Yantai 264001, China
2.
Unit 91115 of the PLA, Zhoushan 316000, China
3.
School of Computer Science, Jiangsu University of Science and Technology, Zhenjiang 212003, China

Funds:

National Natural Science Foundation of China 51605487

More Information

Corresponding author: TENG Kenan, E-mail: Tengkn@sina.com

摘要

摘要:
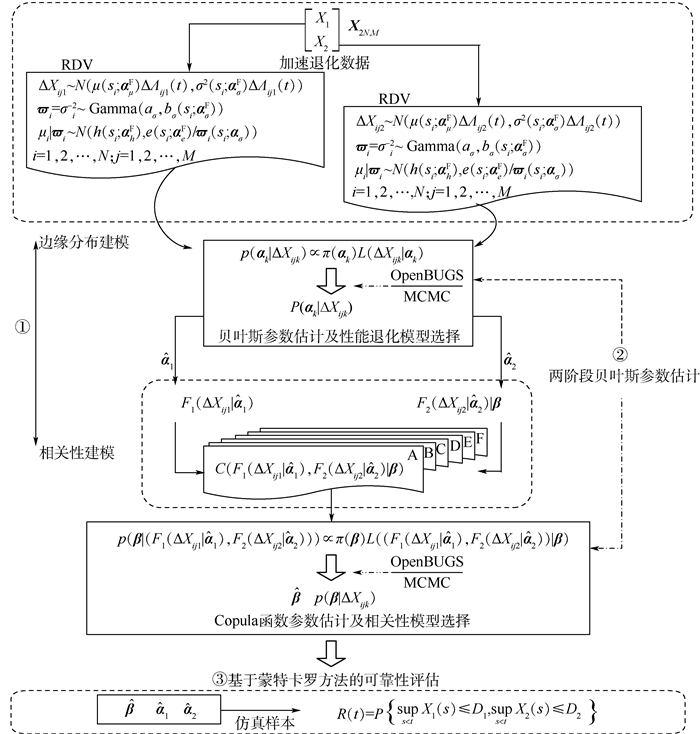
针对加速应力下电子部件二元相关退化可靠性分析难题，提出一种基于随机相关的可靠性分析方法。采用考虑个体差异的Wiener过程模型建立边缘退化过程模型，并基于加速因子不变原则建立了模型参数与加速应力的关系；构建了基于Copula函数的随机相关模型，采用两阶段贝叶斯参数估计方法进行参数估计，综合运用散点图、偏差信息准则（DIC）值以及Kendall τ的非参数估计值等方法进行随机相关模型选择，并采用蒙特卡罗仿真方法进行可靠度计算。最后采用实例验证了所提方法有效性，为考虑个体差异的贮存可靠性评估提供了技术支撑。
- 可靠性评估 /
- 加速退化数据 /
- 二元退化 /
- 随机相关 /
- 电子部件
Abstract:
Targeting at the difficulty of reliability analysis for electronic components with bivariate correlation accelerated degradation data, a reliability assessment method based on random correlation is proposed. The Wiener process model with random effect is used to model the marginal degradation process considering the individual difference, and the relationship between model parameters and acceleration stress is established by using acceleration factor constant principle. Then, a bivariate degradation model with random correlation based on Copula function is established. A two-stage Bayesian method is introduced to facilitate the parameter estimation, and the scatter plots, deviance information criterion (DIC) and the non-parametric estimation of Kendall τ are used for random correlation model selection. The reliability calculation is carried out by Monte Carlo simulation method. Finally, an example is used to verify the effectiveness of the proposed method.The paper has significant meaning for the storage reliability assessment considering individual differences.
- reliability assessment /
- accelerated degradation data /
- bivariate degradation /
- random correlation /
- electronic component

HTML全文

图 1 二元相关退化建模框架

Figure 1. Framework of bivariate correlation degradation modeling

下载: 全尺寸图片幻灯片

图 2 X₁和X₂的随机参数箱线图

Figure 2. Boxplots of random parameters of X₁ and X₂

下载: 全尺寸图片幻灯片

图 3 3个加速应力下的边缘退化增量累积分布函数取值的散点图

Figure 3. Scatter plots of CDFs of degradation increments under three accelerated stresses

下载: 全尺寸图片幻灯片

图 4 边缘退化增量累积分布函数取值的散点图

Figure 4. Scatter plot of CDFs of degradation increments

下载: 全尺寸图片幻灯片

图 5 随机相关性模型参数的箱线图

Figure 5. Boxplots of parameters of random correlation model

下载: 全尺寸图片幻灯片

图 6 可靠度曲线

Figure 6. Reliability curves

下载: 全尺寸图片幻灯片

表 1 Copula函数

Table 1. Copula function

Copula函数	分布函数C(u, v; θ)	θ	τ
Frank
Gaussian
Gumbel
Clayton

下载: 导出CSV

表 2 边缘分布参数估计值

Table 2. Parameter estimations of marginal distribution

寿命表征参数	参数	均值	置信区间(置信水平为0.95)	先验
X₁	_RDV(1)	1.338	[0.111 9，2.778]	U(0, 100)
	_RDV(2)	906.2	[689.1，997.3]	U(0, 1 000)
	_RDV(3)	0.530 3	[0.016 53，1.678]	U(0, 100)
	_RDV(4)	0.444 5	[0.018 11，1.206]	U(0, 100)
		0.259 6	[0.158 9，0.359 6]	U(0, 10)
		4.448	[1.288，9.462]	U(0, 10)
X₂	_RDV(1)	2.901	[1.23，4.303]	U(0, 100)
	_RDV(2)	823.4	[465.8，994.4]	U(0, 1 000)
	_RDV(3)	0.651 5	[0.021 36, 1.983]	U(0, 100)
	_RDV(4)	1.058	[0.084 9, 2.11]	U(0, 100)
		0.217	[0.126 9, 0.309 5]	U(0, 10)
		6.027	[1.729, 9.793]	U(0, 10)

下载: 导出CSV

表 3 Copula函数参数估计值

Table 3. Parameter estimations of Copula function

模型	参数	均值	先验	DIC值	τ
Gaussian模型A	θ	0.158 1	U(-1, 1)	179	0.101 1
Frank模型A	θ	2.897	U(0, 100)	-14.07	0.298 1
Gumbel模型A	θ	1.302	U(1, 100)	-11.46	0.232 0
Clayton模型A	θ	0.558	U(0, 100)	-12.18	0.218 2

下载: 导出CSV

表 4 随机相关模型参数估计值

Table 4. Parameter estimations of random correlation models

模型	参数	均值	置信区间(置信水平为0.95)	先验	DIC值
A	θ	2.897	[1.493，4.288]	(0, 100)	-14.07
B	γ_B(1)	1.433	[0.544 7，2.195]	(0, 100)	-13.64
B	γ_B(2)	190.4	[8.855，388.4]	(0, 400)	-13.64
C	a_θ	3.677	[1.615，6.332]	(0, 100)	-16.45
C	b_θ	2.357	[0.228 2，5.605]	(0, 100)	-16.45
D	γ_D(1)	14.2	[0.904 6，43.15]	(0, 100)	-13.61
	γ_D(2)	9 280	[154.6，19 590]	(0, 20 000)
	b_θ	4.29	[0.727 5，9.157]	(0, 100)
E	γ_E(1)	2.706	[0.159 9, 5.845]	(0, 100)	-15.18
	γ_E(2)	1 139	[90.83，1 963]	(0, 2 000)
	a_θ	3.416	[1.628，5.748]	(0, 100)
F	γ_F(1)	3.161	[0.905，6.113]	(0, 100)	-13.66
	γ_F(2)	813.9	[29.4，1 909]	(0, 2 000)
	γ_F(3)	2.193	[0.138 2，4.711]	(0, 100)
	γ_F(4)	830	[58.14，1 471]	(0, 1 500)

下载: 导出CSV

参考文献(18)

[1]	WANG X.Wiener processes with random effects for degradation data[J].Journal of Multivariate Analysis, 2010, 101(1):340-351. https://www.sciencedirect.com/science/article/pii/S0047259X08002777
[2]	YE Z S, CHEN N, SHEN Y.A new class of Wiener process models for degradation analysis[J].Reliability Engineering & System Safety, 2015, 139(1):58-67. http://cn.bing.com/academic/profile?id=c67a6fbe7cbe36b0b40dd877b1b06dc0&encoded=0&v=paper_preview&mkt=zh-cn
[3]	RODRÍGUEZ-PICÓN L.Reliability assessment for systems with two performance characteristics based on gamma processes with marginal heterogeneous random effects[J].Eksploatacja I Niezawodnosc-Maintenance and Reliability, 2017, 19(1):8-18.
[4]	PENG W W, LI Y, YANG Y, et al.Inverse Gaussian process models for degradation analysis:A Baysian perspective[J].Reliability Engineering & System Safety, 2014, 130(6):175-189. http://cn.bing.com/academic/profile?id=38912dfb94e04b37c75fa3406274a738&encoded=0&v=paper_preview&mkt=zh-cn
[5]	YE Z S, CHEN N.The inverse Gaussian process as a degradation model[J].Technometrics, 2014, 56(3):302-311. doi: 10.1080/00401706.2013.830074
[6]	PADGETT W J, TOMLINSON M A.Inference from accelerated degradation and failure data based on Guassian process models[J].Lifetime Data Analysis, 2004, 10(2):191-206. doi: 10.1023/B:LIDA.0000030203.49001.b6
[7]	潘正强, 周经伦, 彭宝华.基于Wiener过程的多应力加速退化试验设计[J].系统工程理论与实践, 2009, 29(8):64-71. doi: 10.3321/j.issn:1000-6788.2009.08.008 PAN Z Q, ZHOU J L, PENG B H.Design of accelerated degradation tests with several stresses based on Wiener process[J].Systems Engineering-Theory & Practice, 2009, 29(8):64-71(in Chinese). doi: 10.3321/j.issn:1000-6788.2009.08.008
[8]	LIM H, YUM B J.Optimal design of accelerated degradation tests based on Wiener process models[J].Journal of Applied Statistics, 2011, 38(2):309-325. doi: 10.1080/02664760903406488
[9]	SUNG S, YUM B J.Optimal design of step-stress accelerated degradation tests based on the Wiener degradation process[J].Quality Technology & Quantitative Management, 2016, 13(4):367-393. http://cn.bing.com/academic/profile?id=ef1da9d81d85cfbbf8eabb592aac231c&encoded=0&v=paper_preview&mkt=zh-cn
[10]	WHITMORE G A, SCHENKELBERG F.Modelling accelerated degradation data using Wiener diffusion with a time scale transformation[J].Lifetime Data Analysis, 1997, 3(1):27-45. doi: 10.1023/A:1009664101413
[11]	HAN W, YU Z, MA X B.Mechanism equivalence in designing optimum step-stress accelerated degradation test plan under Wiener process[J].IEEE Access, 2018, 6:4440-4451. doi: 10.1109/ACCESS.2018.2789518
[12]	王浩伟, 徐廷学, 赵建忠.融合加速退化和现场实测退化数据的剩余寿命预测方法[J].航空学报, 2014, 35(12):3350-3357. http://d.old.wanfangdata.com.cn/Periodical/hkxb201412016 WANG H W, XU T X, ZHAO J Z.Residual life prediction method fusing accelerated degradation data and field degradation data[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(12):3350-3357(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hkxb201412016
[13]	盖炳良, 滕克难, 王浩伟, 等.基于加速因子的Wiener退化产品可靠性评估方法[J].战术导弹技术, 2017(6):25-30. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zsddjs201706005 GAI B L, TENG K N, WANG H W, et al.Reliability assessment approach for Wiener-type degradation based on acceleration factor[J].Tactical Missile Technology, 2017(6):25-30(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zsddjs201706005
[14]	盖炳良, 滕克难, 王浩伟, 等.基于加速因子不变原则的加速度计可靠性分析[J].中国惯性技术学报, 2018, 26(6):835-840. http://d.old.wanfangdata.com.cn/Periodical/zggxjsxb201806022 GAI B L, TENG K N, WANG H W, et al.Reliability analysis for accelerometers based on invariant principle of acceleration factor[J].Journal of Chinese Inertial Technology, 2018, 26(6):835-840(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/zggxjsxb201806022
[15]	王浩伟, 滕克难, 李军亮.随机环境应力冲击下基于多参数相关退化的导弹部件寿命预测[J].航空学报, 2016, 37(11):3404-3412. http://d.old.wanfangdata.com.cn/Periodical/hkxb201611018 WANG H W, TENG K N, LI J L.Lifetime prediction for missile components based on multiple parameters correlative degrading with random shocks of environmental stresses[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(11):3404-3412(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hkxb201611018
[16]	盖炳良, 滕克难, 唐金国, 等.基于马氏距离的二元退化可靠性分析[J].系统工程与电子技术, 2019, 41(3):686-692. http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201903032 GAI B L, TENG K N, TANG J G, et al.Reliability analysis for bivariate degradation process based on Mahalanobis distance[J].Systems Engineering and Electronics, 2019, 41(3):686-692(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/xtgcydzjs201903032
[17]	张志鹏.系统多元相关退化过程建模及可靠度评估方法研究[D].成都: 电子科技大学, 2016: 19-20. ZHANG Z P.Multivariate correlated degradation modeling and reliability assessment for engineering systems[D].Chengdu: University of Electronic Science and Technology of China, 2016: 19-20(in Chinese).
[18]	申晔.多退化系统加速退化试验方法与应用研究[D].长沙: 国防科学技术大学, 2011: 41-43. SHEN Y.Research on methods and applications of accelerated degradation testing for multiple degradation system[D].Changsha: National University of Defense Technology, 2011: 41-43(in Chinese).