Non-orthogonal multiple-relaxation-time lattice Boltzmann simulation of natural convection in porous square cavity with internal heat source
-
摘要:
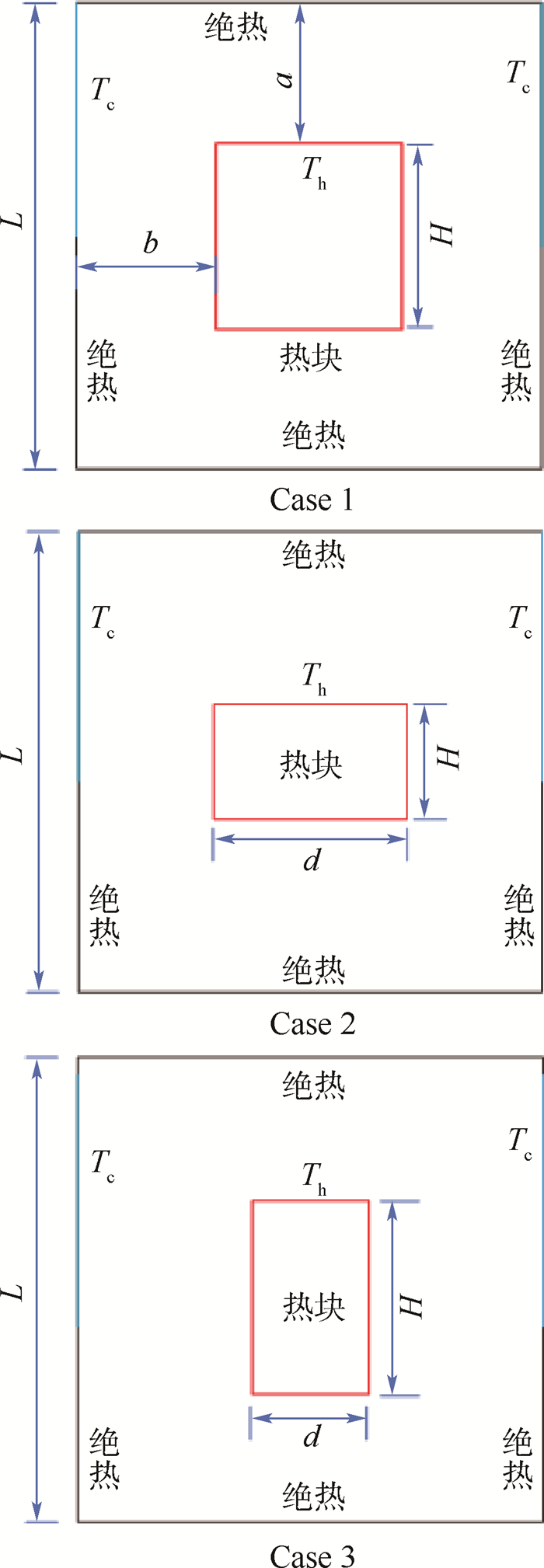
为了增强多孔方腔内流体流动与传热效果，采用非正交多松弛格子Boltzmann方法（MRT-LBM）对含有内热源的多孔方腔自然对流传热现象进行了数值模拟。研究了不同冷源布置方案（Scheme A~Scheme F）、内热源结构形式（Case 1、Case 2、Case 3）、内热源位置（
a 、b ）、Darcy数、Rayleigh数等对多孔方腔内流体流动与传热的影响。计算结果表明：冷源布置方案对腔内流体流动与传热具有重要影响，当冷源左右对称布置时，腔内温度场及流场亦对称分布；在高Rayleigh数下采用Scheme A的双上部冷源布置方案能明显提高腔内的传热强度；内热源的形状对腔内对流传热影响很大，高Rayleigh数下，Case 3的布置方式更好。内热源的位置a 和b 对腔内的传热影响明显，提出了热壁面平均Nusselt数与位置a 的拟合关系式，存在最佳的位置a （a =0.25），使得腔内的对流传热最强；热壁面平均Nusselt数亦随b 值变化表现出特定的变化规律。随着b 值的增加，热壁面平均Nusselt数呈现先增后减再增的趋势。-
关键词:
- 多松弛(MRT)格子 /
- Boltzmann模型 /
- 内热源 /
- 自然对流 /
- 多孔方腔
Abstract:In order to enhance the effect of fluid flow and heat transfer in the porous square cavity, the non-orthogonal multiple-relaxation-time (MRT) lattice Boltzmann method (LBM) is used to simulate the natural convective heat transfer in the porous square cavity with internal heat source. The effects of different cold source arrangements (Scheme A-Scheme F), internal heat source structure (Case 1, Case 2, Case 3), internal heat source location (
a ,b ), Darcy number, and Rayleigh number on fluid flow and heat transfer in square cavity are studied. The calculation results show that the arrangement of the cold source has an important influence on the fluid flow and heat transfer. When the cold source is symmetrically distributed, the temperature field and the flow field in the cavity are also symmetrically distributed; under high Rayleigh number, the double upper cold source arrangement of Scheme A can significantly improve the heat transfer intensity in the cavity; the shape of the internal heat source has a great influence on the convective heat transfer in the cavity. Under the high Rayleigh number, case 3 is arranged better. The positionsa andb of the internal heat source have obvious influence on the heat transfer in the cavity. The fitting relationship between the average Nusselt number of the hot wall surface and the positiona is proposed, and there is an optimal positiona (a =0.25), which makes the convective heat transfer in the cavity strongest; the average Nusselt number of the hot wall surface also shows a specific variation law with the change ofb value. With the value ofb increases, the average Nusselt number of the hot wall surface increases first, then decreases and finally increases. -
图 2 六种不同等温冷源边界布置方案
Figure 2. Six different isothermal cold source boundary arrangements
图 3 不同方法流线及等温线图比较(Ra=106，Da=10-4，ε=0.4， Pr=1.0)
Figure 3. Comparison of streamlines and isotherms with different methods (Ra=106, Da=10-4, ε=0.4, Pr=1.0)
图 4 六种不同等温边界布置下的等温线图和流线图
Figure 4. Isotherms and streamlines for six different isothermal boundary arrangements
图 5 六种不同等温边界布置下的速度分布
Figure 5. Velocity profiles with six different isothermal boundary arrangements
图 6 六种不同等温边界布置下热壁面平均Nusselt数随Darcy数变化
Figure 6. Variation of average Nusselt number at hot wall surface with Darcy number under six different isothermal boundary arrangements
图 7 六种不同等温边界布置下热壁面平均Nusselt数随Rayleigh数变化
Figure 7. Variation of average Nusselt number at hot wall surface with Rayleigh number under six different isothermal boundary arrangements
图 8 六种不同等温边界布置下热壁面局部Nusselt数变化
Figure 8. Variation of local Nusselt number at hot wall surface with six different isothermal boundary arrangements
图 9 三种不同内热源结构形式下方腔内的流线图和等温线图
Figure 9. Streamlines and isotherms in square carity under three different internal heat source structures
图 10 三种不同内热源结构形式下热壁面平均Nusselt数随Rayleigh数变化
Figure 10. Variation of average Nusselt number at hot wall surface with Rayleigh number in cavity under three different heat source structures
图 11 三种不同内热源结构形式下的速度分布
Figure 11. Velocity profiles in cavity under three different internal heat source structures
图 12 不同a值下方腔内的等温线图和流线图
Figure 12. Isotherms and streamlines in square cavity at different values of a
图 13 不同a值下热壁面局部Nusselt数变化
Figure 13. Variation of local Nusselt number at hot wall surface under different a values
图 14 热壁面平均Nusselt数随a值变化
Figure 14. Average Nusselt number at hot wall under different surface versus a values
图 15 不同b值下方腔内的等温线图和流线图
Figure 15. Isotherms and streamlines in square cavity at different values of b
图 16 不同b值下方腔水平中平面的速度分布
Figure 16. Velocity profiles in the horizontal mid-plane of square cavity under different b values
图 17 热壁面平均Nusselt数随b值变化
Figure 17. Average Nusselt number at hot wall surface versus b values
图 18 不同b值下热壁面局部Nusselt数变化
Figure 18. Variation of local Nusselt number at hot wall surface under different b values
-
[1] NIELD D A, BEJAN A.Convection in porous media[M].Hoboken:Wiley-Blackwell, 2013. [2] AHMED S E, HUSSEIN A K, MOHAMMED H A, et al.Viscous dissipation and radiation effects on MHD natural convection in a square enclosure filled with a porous medium[J].Nuclear Engineering and Design, 2014, 266:34-42. doi: 10.1016/j.nucengdes.2013.10.016 [3] 邱伟国, 云和明, 陈宝明, 等.壁面覆盖部分多孔介质方腔自然对流流动的数值模拟[J].节能, 2014(11):19-23. http://d.old.wanfangdata.com.cn/Periodical/jien201411006QIU W G, YUN H M, CHEN B M, et al.Numerical simulation of natural convection flow in cavity with wall covering part of porous media[J].Energy Conservation, 2014(11):19-23(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/jien201411006 [4] YAACOB Z, HASAN M K.Nonstandard finite difference schemes for natural convection in an inclined porous rectangular cavity[C]//International Conference on Electrical Engineering and Informatics.Piscataway, NJ: IEEE Press, 2015: 665-669. https://www.researchgate.net/publication/308863904_Nonstandard_finite_difference_schemes_for_natural_convection_in_an_inclined_porous_rectangular_cavity [5] 郭照立, 郑楚光.格子Boltzmann方法的原理及应用[M].北京:科学出版社, 2009.GUO Z L, ZHENG C G.Theory and applications of lattice Boltzmann method[M].Beijing:Science Press, 2009(in Chinese). [6] MACHADO R.Numerical simulations of surface reaction in porous media with lattice Boltzmann[J].Chemical Engineering Science, 2012, 69(1):628-643. doi: 10.1016/j.ces.2011.11.037 [7] SHOKOUHMAND H, JAM F, SALIMPOUR M R.Simulation of laminar flow and convective heat transfer in conduits filled with porous media using lattice Boltzmann method[J].International Communications in Heat and Mass Transfer, 2009, 36(4):378-384. doi: 10.1016/j.icheatmasstransfer.2008.11.016 [8] 陆威, 王婷婷, 徐洪涛, 等.复合方腔顶盖驱动双扩散混合对流格子Boltzmann模拟[J].工程热物理学报, 2017, 38(3):640-647. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb201703031LU W, WANG T T, XU H T, et al.Lattice Boltzmann simulation of double diffusive mixed convection in a lid-driven composite enclosure[J].Journal of Engineering Thermophysics, 2017, 38(3):640-647(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gcrwlxb201703031 [9] HUELSZ G, RECHTMAN R.Heat transfer due to natural convection in an inclined square cavity using the lattice Boltzmann equation method[J].International Journal of Thermal Sciences, 2013, 65:111-119. doi: 10.1016/j.ijthermalsci.2012.09.009 [10] ZHAO C Y, DAI L N, TANG G H, et al.Numerical study of natural convection in porous media(metals)using lattice Boltzmann method(LBM)[J].International Journal of Heat and Fluid Flow, 2010, 31(5):925-934. doi: 10.1016/j.ijheatfluidflow.2010.06.001 [11] BOUARNOUNA K, BOUTRA A, RAGUI K, et al.Multiple-relaxation-time lattice Boltzmann model for flow and convective heat transfer in channel with porous media[J].Journal of Statistical Physics, 2019, 174(5):972-991. doi: 10.1007/s10955-018-02219-7 [12] 李培生, 李伟, 张莹, 等.倾斜多孔方腔内自然对流非正交MRT-LB数值模拟[J].华南理工大学学报(自然科学版), 2018, 46(1):15-23. http://d.old.wanfangdata.com.cn/Periodical/hnlgdxxb201801003LI P S, LI W, ZHANG Y, et al.Lattice Boltzmann simulation of natural convection in an inclined porous cavity with a hot square obstacle[J].Journal of Harbin Engineering University(Natural Science Edition), 2018, 46(1):15-23(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/hnlgdxxb201801003 [13] BAYTAS A C, POP I.Free convection in a square porous cavity using a thermal nonequilibrium model[J].International Journal of Thermal Sciences, 2002, 41(9):861-870. doi: 10.1016/S1290-0729(02)01379-0 [14] SAEID N H.Conjugate natural convection in a porous enclosure: Effect of conduction in one of the vertical walls[J].International Journal of Thermal Sciences, 2007, 46(6):531-539. doi: 10.1016/j.ijthermalsci.2006.08.003 [15] AL-FARHANY K, TURAN A.Numerical study of double diffusive natural convective heat and mass transfer in an inclined rectangular cavity filled with porous medium[J].International Communications in Heat and Mass Transfer, 2012, 39(2):174-181. doi: 10.1016/j.icheatmasstransfer.2011.11.014 [16] LIU Q, HE Y L, LI Q, et al.A multiple-relaxation-time lattice Boltzmann model for convection heat transfer in porous media[J].International Journal of Heat and Mass Transfer, 2014, 73:761-775. doi: 10.1016/j.ijheatmasstransfer.2014.02.047 [17] LIU Q, HE Y L, DAWSON K A, et al.Lattice Boltzmann simulations of convection heat transfer in porous media[J].Physica A-Statistical Mechanics and Its Applications, 2017, 465:742-753. doi: 10.1016/j.physa.2016.08.010 -
下载:
点击查看大图
计量
- 文章访问数: 899
- HTML全文浏览量: 154
- PDF下载量: 371
- 被引次数: 0
