Sensitivity analysis for aviation insecure event using Monte-Carlo method under uncertain conditions
-
摘要:
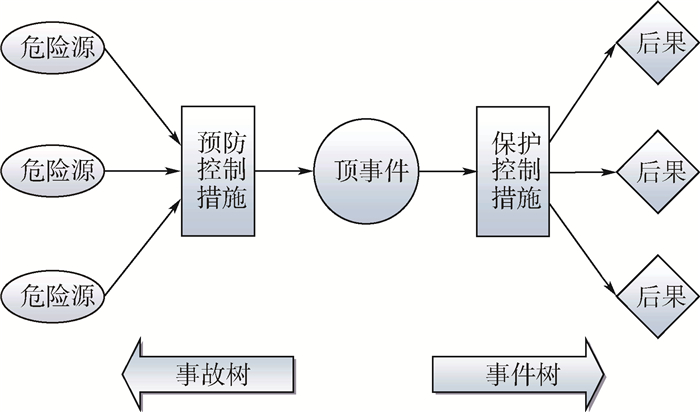
为解决不确定条件下航空不安全事件灵敏度分析的难题，基于Bow-tie模型提出了多模式下航空安全性指标及其灵敏度测度，以轮胎爆破事件为例，采用Monte-Carlo方法计算得到安全性指标、基本事件的全局灵敏度及其分布参数的局部灵敏度。根据轮胎爆破事件仿真结果，两类灵敏度指标均随着飞行时间的增加而发生变化，尤其是在500~600 h时变化最为显著，但灵敏度重要性排序保持不变；基本事件类型是影响灵敏度的一个主要因素，电子类基本事件灵敏度测度远远小于机械类基本事件；同类型基本事件中，平均故障间隔时间不是主导因素，灵敏度大小还与失效传递的逻辑关系密切相关。算例结果表明：航空安全水平随着飞行时间逐步下降，应重点关注飞行时间为500~600 h时航空组件失效导致事故发生的可能性；航空组件的灵敏度重要性不会随着飞行时间变化，提高灵敏度较高的基本事件的可靠性水平是防范航空事故的关键。
-
关键词:
- 航空安全 /
- 灵敏度 /
- 不确定性 /
- Bow-tie模型 /
- Monte-Carlo方法
Abstract:To solve the problem of sensitivity analysis of aviation insecure events under uncertain conditions, this paper proposes the aviation safety index and its sensitivity measurement based on the Bow-tie model. Taking the tire burst accident as an example, we calculate the aviation safety index, the global sensitivity for basic event and its local sensitivity for distribution parameters using Monte-Carlo method. According to the simulation results of the tire burst accident, both types of sensitivity indexes vary with the increasing flight hour, and the most significant change appears during 500-600 h, but with the same order of index importance. The type of basic events is the main factor affecting sensitivity, for the sensitivity of electronic events is far less than the mechanical events. In the uniform type of basic events, the mean time before failure is not the leading factor affecting the sensitivity, which has a close relationship with the failure transferring logic. The results of this example demonstrate that the safety index descends with the flight hour, and the focus for improving aviation safety is to pay attention to accident caused by aviation components failures in 500-600 h. The importance of sensitivity will not change with the flight hour, and the key of preventing aviation accident is to improve the degree of reliability for basic events with a higher sensitivity.
-
Key words:
- aviation safety /
- sensitivity /
- uncertainty /
- Bow-tie model /
- Monte-Carlo method
-
图 3 Monte-Carlo方法的航空安全灵敏度仿真流程
Figure 3. Simulation flowchart of aviation safety sensitivity using Monte-Carlo method
图 4 不确定条件下轮胎爆破事件航空安全性指标
Figure 4. Aviation safety index of tire burst accident under uncertain conditions
图 6 机械类基本事件分布参数μ局部灵敏度
Figure 6. Local sensitivity for distribution parameter μ of mechanical events
图 7 电子类基本事件分布参数λ局部灵敏度
Figure 7. Local sensitivity for distribution parameter λ of electronic events
图 8 机械类基本事件分布参数σ局部灵敏度
Figure 8. Local sensitivity for distribution parameter σ of mechanical events
表 1 轮胎爆破基本事件分布参数及其类型描述
Table 1. Distribution parameters and type description of basic events for tire burst accident
编号 基本事件 基本事件分布类型 分布参数 平均故障间隔时间/h 统计量分布类型 变异系数 BE1 轮毂裂纹 对数正态分布 μ, σ 3 950 正态分布 0.05 BE2 主轮掉块 对数正态分布 μ, σ 3 700 正态分布 0.05 BE3 刹车盘掉块 对数正态分布 μ, σ 3 050 正态分布 0.05 BE4 热熔塞 对数正态分布 μ, σ 2 125 正态分布 0.05 BE5 轮胎气压异常 对数正态分布 μ, σ 3 350 正态分布 0.05 BE6 充气嘴断裂 对数正态分布 μ, σ 2 085 正态分布 0.05 BE7 机轮磨损 对数正态分布 μ, σ 2 680 正态分布 0.05 BE8 软件指令故障 指数分布 λ 2 550 000 正态分布 0.05 BE9 电路短路 指数分布 λ 780 500 正态分布 0.05 BE10 控制阀故障 指数分布 λ 380 000 正态分布 0.05 BE11 转换阀故障 指数分布 λ 320 000 正态分布 0.05 BE12 液压保险故障 指数分布 λ 360 000 正态分布 0.05 BE13 刹车装置故障 对数正态分布 μ, σ 2 480 正态分布 0.05 BE14 应急转换阀失效 对数正态分布 μ, σ 2 110 正态分布 0.05 BE15 应急液压保险失效 对数正态分布 μ, σ 2 180 正态分布 0.05 BE16 应急刹车装置失效 对数正态分布 μ, σ 2 720 正态分布 0.05 
下载: 导出CSV
表 2 轮胎爆破事故树控制事件不确定性描述
Table 2. Uncertainty description of control events for event tree of tire burst accident
编号 控制事件 取值区间 不确定性描述 SE1 启动应急刹车系统 (0.135, 0.165, 0.15) 均匀分布 SE2 避让飞机和建筑物 (0.153, 0.187, 0.17) 均匀分布 SE3 增设隔离网 (0.090, 0.101, 0.10) 均匀分布 SE4 启动应急消防措施 (0.045, 0.055, 0.05) 均匀分布
下载: 导出CSV
-
[1] BORGONOVO E, PLISCHKE E.Sensitivity analysis:A review of recent advances[J].European Journal of Operational Research, 2016, 248(3):869-887. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.2307/3391241 [2] PIANOSI F, BEVEN K, FREER J, et al.Sensitivity analysis of environment models:A systematic review with practical workflow[J].Environmental Modelling & Software, 2016, 79:214-32. https://www.sciencedirect.com/science/article/pii/S1364815216300287 [3] LI L Y, LU Z Z, WU D Q.A new kind of sensitivity index for multivariate output[J].Reliability Engineering and System Safety, 2016, 147:123-131. doi: 10.1016/j.ress.2015.11.006 [4] CAO J K, DING S T.Sensitivity analysis for design verification of general aviation reciprocating aircraft engine[J].Chinese Journal of Aeronautics, 2012, 25(5):675-680. doi: 10.1016/S1000-9361(11)60433-0 [5] CAO J K, DING S T, DU F R.Surrogate-based sensitivity analysis for safety assement of general aviation heavy-fueled engines[J].Procedia Engineering, 2014, 80:66-75. doi: 10.1016/j.proeng.2014.09.061 [6] ZENTNER I, TARANTOLA S, DE ROCQUIGNY E.Sensitivity analysis for reliable design verification of nuclear turbosets[J].Reliability Engineering and System Safety, 2011, 96:391-397. doi: 10.1016/j.ress.2010.10.005 [7] 金燕, 刘少军.基于人工神经网络的航空轴承疲劳可靠性分析[J].东北大学学报(自然科学版), 2018, 39(6):850-855. http://d.old.wanfangdata.com.cn/Periodical/dbdxxb201806018JIN Y, LIU S J.Fatigue reliability analysis of aviation bearings based on ANN[J].Journal of Northeastern University(Nature Science), 2018, 39(6):850-855(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/dbdxxb201806018 [8] 权凌霄, 张琦玮, 李长春, 等.航空液压管路支架参数灵敏度分析及优化[J].液压与气动, 2017(8):95-99. http://d.old.wanfangdata.com.cn/Periodical/yyyqd201708016QUAN L X, ZHANG Q W, LI C C, et al.Sensitivity analysis and optimization for support parameter of aviation hydraulic pipeline[J].Chinese Hydraulics & Pneumatics, 2017(8):95-99(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/yyyqd201708016 [9] 张马兰, 刘君强, 左洪福, 等.基于区间数学理论和贝叶斯网络指标灵敏度分析[J].武汉理工大学学报(交通科学与工程版), 2015, 39(1):162-170. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whjtkjdxxb201501037ZHANG M L, LIU J Q, ZUO H F, et al.Sensitivity analysis for indicators based on Bayesian network and interval mathematics[J].Journal of Wuhan University of Technology(Transportation Science and Engineering), 2015, 39(1):162-170(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whjtkjdxxb201501037 [10] 陈超, 吕震宙.模糊分布参数的全局灵敏度分析方法[J].工程力学, 2016, 33(2):25-33. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201602004CHEN C, LV Z Z.A new method for global sensitivity analysis of fuzzy distribution parameters[J].Engineering Mechanics, 2016, 33(2):25-33(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201602004 [11] 锁斌, 曾超, 程永生, 等.认知不确定性下可靠性灵敏度分析的新指标[J].航空学报, 2013, 34(7):1605-1615. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201307012SUO B, ZENG C, CHENG Y S, et al.New index for reliability sensitivity analysis under epistemic uncertainty[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(7):1605-1615(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201307012 [12] CUI L J, ZHANG J K, REN B, et al.Research on a new aviation safety index and its solution under uncertainty conditions[J].Safety Science, 2018, 107:55-61. doi: 10.1016/j.ssci.2018.04.001 [13] PURTON L, CLOTHIER R, KOUROUSIS K.Assessment of technical airworthiness in military aviation:Implementation and further advancement of the Bow-tie model[J].Procedia Engineering, 2014, 80:529-544. doi: 10.1016/j.proeng.2014.09.110 [14] CLOTHIER R A, WILLIAMS B P, HAYHURST K J.Modeling the risks remotely piloted aircraft pose to people on the ground[J].Safety Science, 2018, 101:33-47. doi: 10.1016/j.ssci.2017.08.008 [15] U.S.Department of Defense.Standard practice for system safety: MIL-HDBK-882D[S].Washington, D.C.: U.S.Department of Defense, 2000: 16-20. [16] SAE International.Guidelines for development of civil aircraft systems: ARP4754A[S].Washington, D.C.: SAE International, 2010: 160-162. [17] U.S.Department of Defense.Reliability prediction of electronic equipment: MIL-HDBK-217E[S].Washington, D.C.: U.S.Department of Defense, 1991: 121-125. [18] DAVID R E.Location of commercial aircraft accidents/incidents relative to runways: DOT/FA/AOV 90-1 FINAL REPO[R].Washington, D.C.: FAA, 1990. [19] FAA.System design and analysis: AC25.1309-1A[S].Washington, D.C.: FAA, 1988: 57-63. -
下载:
点击查看大图
计量
- 文章访问数: 720
- HTML全文浏览量: 125
- PDF下载量: 121
- 被引次数: 0
