电磁层析成像中传感器阵列的优化设置

岳远里; 刘泽; 武建利; 苗宇; 刘向龙; 王嘉伟

doi:10.13700/j.bh.1001-5965.2019.0246

电磁层析成像中传感器阵列的优化设置

doi: 10.13700/j.bh.1001-5965.2019.0246

北京交通大学电子信息工程学院, 北京 100044

基金项目:

国家自然科学基金 61771041

详细信息

作者简介:
岳远里  男，硕士研究生。主要研究方向：电磁层析成像

刘泽  男，博士，教授，博士生导师。主要研究方向：过程参数检测、电磁层析成像

苗宇  女，硕士, 讲师, 博士研究生。主要研究方向:深度学习、电磁层析成像及其应用

通讯作者:
苗宇. E-mail: ymiao@bjtu.edu.cn

中图分类号: TP23;TP212
计量
- 文章访问数: 778
- HTML全文浏览量: 194
- PDF下载量: 168
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-22
- 录用日期: 2019-08-19
- 网络出版日期: 2020-02-20

Optimization for settings of sensor array in electromagnetic tomography

School of Electronic Information Engineering, Beijing Jiaotong University, Beijing 100044, China

Funds:

National Natural Science Foundation of China 61771041

More Information

Corresponding author: MIAO Yu. E-mail: ymiao@bjtu.edu.cn

摘要

摘要:
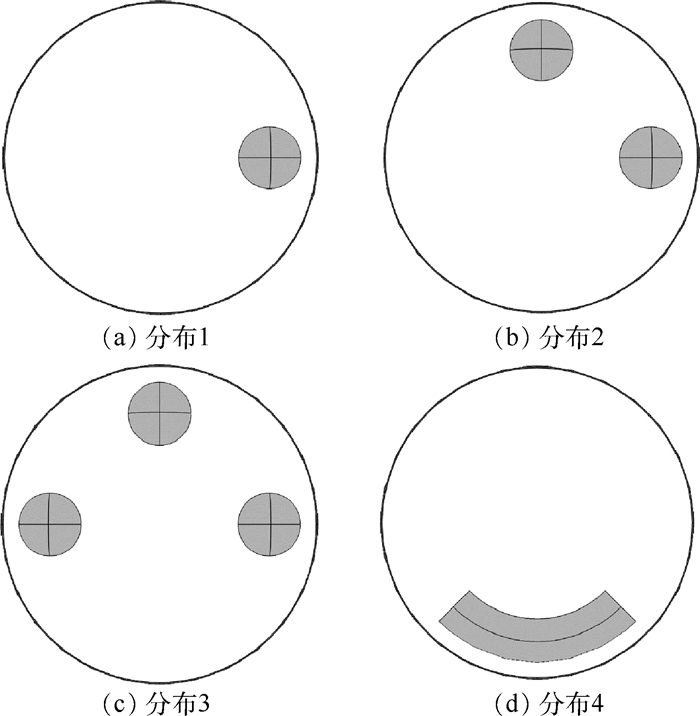
电磁层析成像（EMT）中传感器阵列的设置决定了获得的感应电压测量值的数量，对成像的效果有着重要的影响。为了探究传感器设置对成像质量的影响规律，通过改变传感器阵列中线圈的数量及相对位置对传感器阵列进行优化。在COMSOL Multi-physics中建立不同线圈数量的传感器阵列模型，采用不同的成像算法进行成像并比较成像效果，发现适当增加传感器的个数可以提高成像质量，但增加到一定数量则成像效果下降；同时在传感器阵列固定的情况下将传感器阵列按照一定规则进行旋转，发现旋转之后叠加的复合成像效果要优于未旋转的成像效果。该结果对下一步EMT系统设计中传感器阵列的设置具有一定的指导意义。
- 电磁层析成像(EMT) /
- 感应电压 /
- 传感器阵列 /
- 旋转 /
- 成像质量
Abstract:
The settings of the sensor array in electromagnetic tomography (EMT) determine the number of induced voltages, which have an important influence on reconstructed image quality. To study the effect of the settings of coils on the quality of reconstructed images, the number and the position of the sensor array are discussed for optimization. In this paper, the models with different numbers of coils and different contributions are established by using COMSOL Multi-physics; the different algorithms are used to image reconstruction and the quality of the constructed images was compared by correlation coefficient. The simulation shows that the image quality improved by increasing the number of sensors, but when increased to a certain number, the image quality will become worse if the number of the coils continue to increase. In order to increase the measurement data instead of increasing the number of the sensor array, the sensor array is rotated. By comparing the image quality before and after rotation, the result shows that the quality of the reconstructed image is obviously improved after the combination. The simulation results can be a guide for the settings of the sensor array in the design of the EMT system in future work.
- electromagnetic tomography (EMT) /
- induced voltage /
- sensor array /
- rotated /
- image quality

HTML全文

图 1 正问题与逆问题的关系

Figure 1. Relationship between forward and inverse problems

下载: 全尺寸图片幻灯片

图 2 不同数量线圈的传感器阵列模型

Figure 2. Sensor array models with different numbers of coils

下载: 全尺寸图片幻灯片

图 3 不同物场分布模型

Figure 3. Different object field distribution models

下载: 全尺寸图片幻灯片

图 4 感应电压测量值

Figure 4. Induced voltage measurements

下载: 全尺寸图片幻灯片

图 5 等分节点次序

Figure 5. Order of equant nodes

下载: 全尺寸图片幻灯片

图 6 不同激励-检测对的灵敏度矩阵

Figure 6. Sensitivity matrix of different excitation-detection

下载: 全尺寸图片幻灯片

图 7 传感器阵列旋转前后对比示意图

Figure 7. Comparison before and after rotation of sensor array

下载: 全尺寸图片幻灯片

图 8 10线圈图像重建

Figure 8. Reconstructed images with 10 coils

下载: 全尺寸图片幻灯片

图 9 12线圈图像重建

Figure 9. Reconstructed images with 12 coils

下载: 全尺寸图片幻灯片

图 10 16线圈图像重建

Figure 10. Reconstructed images with 16 coils

下载: 全尺寸图片幻灯片

图 11 20线圈图像重建

Figure 11. Reconstructed images with 20 coils

下载: 全尺寸图片幻灯片

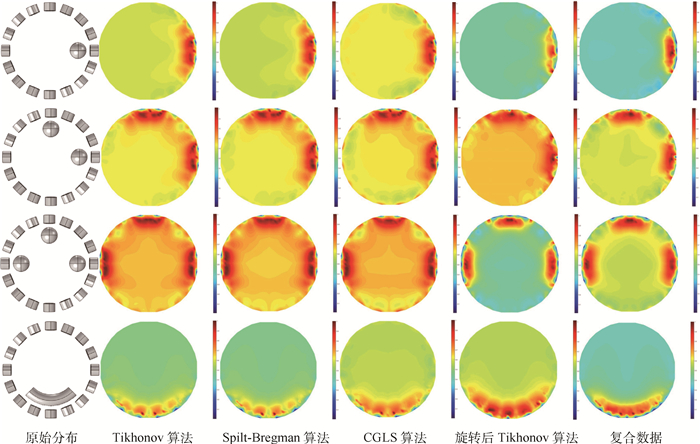
表 1 10线圈相关系数

Table 1. Correlation coefficient with 10 coils

分布	Tikhonov 算法	Spilt-Bregman 算法	CGLS 算法	旋转后 Tikhonov算法	复合数据
分布1	0.356 1	0.366 1	0.371 0	0.487 6	0.491 4
分布2	0.355 9	0.386 5	0.372 7	0.405 1	0.434 6
分布3	0.277 8	0.277 8	0.293 4	0.416 2	0.409 5
分布4	0.642 7	0.642 8	0.659 1	0.697 4	0.723 0

下载: 导出CSV

表 2 12线圈相关系数

Table 2. Correlation coefficient with 12 coils

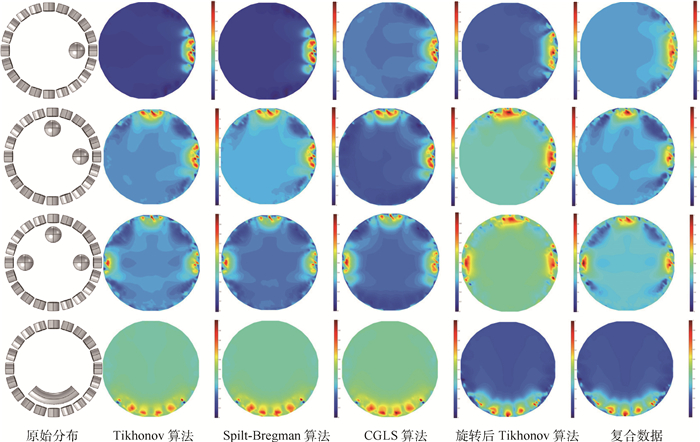
分布	Tikhonov 算法	Spilt-Bregman 算法	CGLS 算法	旋转后 Tikhonov算法	复合数据
分布1	0.436 8	0.435 0	0.452 8	0.452 1	0.499 2
分布2	0.396 5	0.400 4	0.406 3	0.455 8	0.495 3
分布3	0.365 6	0.364 6	0.374 7	0.423 0	0.460 7
分布4	0.736 8	0.741 4	0.750 8	0.760 9	0.770 0

下载: 导出CSV

表 3 16线圈相关系数

Table 3. Correlation coefficient with 16 coils

分布	Tikhonov 算法	Spilt-Bregman 算法	CGLS 算法	旋转后 Tikhonov算法	复合数据
分布1	0.426 1	0.426 4	0.416 3	0.440 4	0.469 6
分布2	0.376 5	0.376 7	0.390 5	0.433 4	0.442 6
分布3	0.376 6	0.387 3	0.397 8	0.416 0	0.448 8
分布4	0.644 7	0.644 9	0.640 0	0.673 4	0.711 3

下载: 导出CSV

表 4 20线圈相关系数

Table 4. Correlation coefficient with 20 coils

分布	Tikhonov 算法	Spilt-Bregman 算法	CGLS 算法	旋转后 Tikhonov算法	复合数据
分布1	0.438 3	0.418 7	0.445 2	0.468 2	0.475 8
分布2	0.433 9	0.432 3	0.427 0	0.440 6	0.484 4
分布3	0.388 5	0.403 6	0.396 7	0.421 4	0.443 0
分布4	0.552 5	0.550 1	0.597 2	0.594 2	0.594 9

下载: 导出CSV

参考文献(20)

[1]	王化祥, 崔自强, 许燕斌, 等.电学层析成像技术及应用[C]//2009年中国自动化大会暨两化融合高峰会议, 2009: 1-13. WANG H X, CUI Z Q, XU Y B, et al.Electrical tomography: State of the art[C]//2009 China Automation Conference and Integration Conference, 2009: 1-13(in Chinese).
[2]	YIN W, PEYTON A J.A planar EMT system for the detection of faults on thin metallic plates[J].Measurement Science and Technology, 2006, 17(8):2130-2135. doi: 10.1088/0957-0233/17/8/011
[3]	TERZIJA N, YIN W L, GERBETH G, et al.Electromagnetic inspection of a two-phase flow of GaInSn and argon[J].Flow Measurement and Instrumentation, 2011, 22(1):10-16. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=128b3ef0eb657572ee3048b03d530e88
[4]	GRIFFITHS H, STEWART W R, GOUGN W.Magnetic induction tomography:A measuring system for biological tissues[J].Annals of the New York Academy of Sciences, 1999, 873(1):335-345. doi: 10.1111-j.1749-6632.1999.tb09481.x/
[5]	PEYTON A J, BECK M S, BORGES A R, et al.Development of electromagnetic tomography (EMT) for industrial applications.Part1:Sensor design and instrumentation[C]//1st World Congress on Industrial Process Tomography, 1999:306-312.
[6]	ZAKARIA Z, RAHIM R A, SAIFUL M, et al.Advancement in transmitters and sensors for biological tissue imaging in magnetic induction tomography[J].Sensors, 2012, 12:7126-7156. doi: 10.3390/s120607126
[7]	BORGES A R, DE OLIVEIRA J E, VELEA J, et al.Development of electromagnetic tomography(EMT) for industrial applications.Part2:Image reconstruction and software framework[C]//1st World Congress on Industrial Process Tomography, 1999:14-17.
[8]	PEYTON A J, YU Z Z, LYON G, et al.An overview of electromagnetic inductance tomography:Description of three different systems[J].Measurement Science and Technology, 1993, 7(3):261-271. doi: 10.1088-0957-0233-7-3-006/
[9]	LIU Z, LI W, XUE F, et al.Electromagnetic tomography rail defect inspection[J].IEEE Transactions on Magnetics, 2015, 51(10):1-7. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0235383759/
[10]	XIE C G, HUANG S M, HOYLE B S, et al.Electrical capacitance tomography for flow imaging:System model for development of image reconstruction algorithms and design of primary sensor[J].IEEE Proceedings G, 1992, 139(1):89-98. https://ieeexplore.ieee.org/document/125122/
[11]	KTISTIS C, ARMITAGE D W, PEYTON A J.Calculation of the forward problem for absolute image reconstruction in MIT[J].Physiological Measurement, 2008, 29:455-464. doi: 10.1088/0967-3334/29/6/S38
[12]	XIONG H L, XU L A.Electromagnetic tomography(EMT):Theoretical analysis of the forward problem[J].Applied Mathematics and Mechanics(English Edition), 2000, 21(9):1034-1044. doi: 10.1007/BF02459313
[13]	YIN W L, PEYTON A J, STEFANI F, et al.Theoretical and numerical approaches to the forward problem and sensitivity calculation of a novel contactless inductive flow tomography(CIFT)[J].Measurement Science and Technology, 2009, 20(10):105503. doi: 10.1088/0957-0233/20/10/105503
[14]	徐凯, 陈广, 尹武良, 等.基于场量提取法的电磁层析成像系统的灵敏度推算[J].传感技术学报, 2011, 24(4):543-547. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cgjsxb201104015 XU K, CHEN G, YIN W L, et al.Sensitivity estimation of electromagnetic tomography system based on field volume extraction method[J].Journal of Transduction Technology, 2011, 24(4):543-547(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cgjsxb201104015
[15]	LIU Z J, BABOUT L, BANASIAK R, et al.Effectiveness of rotatable sensor to improve image accuracy of ECT system[J].Flow Measurement and Instrumentation, 2010, 21(3):219-227. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4b6354430f4570ab66077a04bb42748f
[16]	YANG W Q, PENG L H.Image reconstruction algorithm for electrical capacitance tomography[J].Measurement Science and Technology.2003, 14(1):1-13. doi: 10.1088/0957-0233/14/1/301
[17]	LI F, ABASCAL J F P J, DESCO M, et al.Total variation regularization with Split Bregman-based method in magnetic induction tomography using experimental data[J].IEEE Sensors Journal, 2017, 14(1):976-986. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a1f1434dca830f09f6350860fe2908ca
[18]	LIU L, SHAO F Q.Modified conjugate gradient algorithm for image reconstruction of electromagnetic tomography[J].Chinese Journal of Scientific Instrument, 2010, 31(3):655-658. http://en.cnki.com.cn/Article_en/CJFDTOTAL-YQXB201003032.htm
[19]	XIE C G, HUANG S M, LENN C P, et al.Experimental evaluation of capacitance tomographic flow imaging systems using physical models[J].IEE Proceedings Circuits Devices and Systems, 1994, 141(5):357-368. doi: 10.1049/ip-cds:19941152
[20]	陈晓艳, 常晓敏.基于评价指标的EIT算法参数选择方法研究[J].天津科技大学学报, 2016, 31(6):64-68. http://d.old.wanfangdata.com.cn/Periodical/tjqgyxyxb201606012 CHEN X Y, CHANG X M.Study on parameter selection method of EIT algorithm based on evaluation index[J].Journal of Tianjin University of Science and Technology, 2016, 31(6):64-68(in Chinese). http://d.old.wanfangdata.com.cn/Periodical/tjqgyxyxb201606012